⚛️ 🔈 👊🏿 非線形計画問題の応用 👚 🖕🏾 🧑🏽‍🤝‍🧑🏽

こんにちは、Habr！かつて、私は中学生として、最適化理論と最適な非線形力学系の合成の分野で研究を始めました。ほぼ同時期に、この分野を普及させ、彼らの経験や考えを人々と共有したいという要望がありました。これの確認は、Habréに関する私の~~子供たちの~~未熟な記事のいくつかです。しかし、当時、この考えは私にとって圧倒的でした。おそらく、私の仕事、経験の浅さ、批判やアドバイスで仕事をすることができない、または何か他のもののために。理由を無限に見つけようとすることはできますが、状況は変わりません。このアイデアを棚に投げて、ここまで安全に置いてほこりを払いました。

専門を終えて論文を守る準備をした後、論理的な質問をしました。「次は何ですか？」ほこりの下。しかし、私はより意識的な形でこの考えに戻りました。

私は、8年前から取り組んでいる業界に関連するソフトウェアの開発と、最適化手法や機械学習などの個人的な学問的バイアスの開発を開始することにしました。

さて、興味のある方へ：

卒業証書（およびその後の論文）のソフトウェアの実装に携わっていたので、この問題に「正面から」取り組みました。システムの柔軟性、作成の容易さを気にしませんでした。ここで結果を取得したいという欲求は、経験不足と相まって、コードを絶えず書き直さなければならないという事実につながりましたが、それはもちろん専門的な開発にプラスの影響を与えませんでした。すでに私は、私がどのように望んでも、問題を解決するために真っ向から急ぐことはできないことを理解しています。その本質を掘り下げ、既存の知識を評価し、不足しているものを理解し、サブジェクト領域の概念をクラス、インターフェース、および抽象化と比較する必要があります。つまり、利用可能な埋蔵量を実現し、ソフトウェアアプリケーションのアーキテクチャの設計に適切にアプローチする必要があります。

ご想像のとおり、この記事は将来のアプリケーションの最初の要素の開発と説明に専念します。

開発アプローチの定義と主なタスクの定式化

Habréには、ソフトウェア開発方法論に関する記事が多数あります。たとえば、これは主なアプローチを非常に明確に説明しています。それぞれについて説明しましょう。

「ウォーターフォールモデル」 -少なくとも要件が明確に定義されていないため、適切ではありません。その後、相互作用を確立する必要がある一連のアイデアがあります。
「Vモデル」 -同じ理由で適合しない
「インクリメンタルモデル」は以前のモデルよりも適切なモデルですが、ここでも詳細な形式化が必要です。
「RADモデル」 -経験豊富な専門家のチームにより適したモデル、
「アジャイルモデル」 -要件を指定する必要がないという基準、および開発プロセスの柔軟性に完全に適合しており、
「反復モデル」 -仕事は目標の明確な定義の必要性を示しているという事実にもかかわらず、イデオロギー的に、そのようなモデルは近いようです（「主なタスクを定義する必要がありますが、実装の詳細は時間とともに進化する可能性があります」）、
「スパイラルモデル」 -提案されたソフトウェアに起因することはほとんどない大規模プロジェクトの実装を目的としています。

私はアジャイルモデルの概念を厳守しようとします。開発の反復ごとに、特定の目標と目的のセットが提案されます。これについては、記事でさらに詳しく説明します。

そのため、現時点では一般的な問題の次の定式化があります：開発中のソフトウェアは、さまざまな最適化アルゴリズム（古典的な分析と現代のヒューリスティックの両方）および機械学習（分類、クラスタリング、空間次元削減、回帰）アルゴリズムを実装する必要があります。最後の最終目標は、これらのアルゴリズムを最適制御合成の分野に適用し、金融市場で取引戦略を作成する方法を開発することです。 Scalaが主要な開発言語として選ばれました。

したがって、この作業では次のように伝えます。

最適化の問題と、それを研究の基本的な対象として選択する理由については、
主な抽象化とその実装では、最適化の問題を減らすことにより、適用された問題を解決することに基づいたアプローチを使用できます。
K-Meansアルゴリズム、最も単純なランダム検索アルゴリズム、およびそれらを友達にして単一の目標のために機能させる方法について。

最適化

私はほとんどの研究業務を最適化問題の解決に費やしたという事実により、この観点から操作する方がより便利になります。

通常、最適化問題を解くことにより、どんなに些細で鈍い言語に聞こえても、何らかの「最適な」（問題条件の観点から）オブジェクトの検索を意味します。「最適性」の概念は、主題分野ごとに異なります。たとえば、関数の最小値を見つける問題では、目的関数の最小値に対応する点を見つける必要があります。メタ最適化問題では、最適な制御の合成の問題で、最も正確な結果/最も迅速に満たす/最も安定した結果を与えるアルゴリズムのパラメーターを決定する必要があります最短時間でオブジェクトを最終状態に変換できるコントローラを合成する必要があります。すべての専門家は、彼の専門分野に関連するこのタスクのリストを継続できると確信しています。

数学では、非線形プログラミング問題に特別な注意が払われます。非線形問題には、他の多くの応用問題を減らすことができます。一般的な場合、非線形計画問題の定式化には、以下を指定する必要があります。

任意の関数 $f：\ mathbb {R} ^ n \右矢印\ mathbb {R}$ （特定の品質基準の役割を果たす：最小化問題の場合、最小化に対応するベクトルを見つける必要があり、逆に最大化の場合）、
基本的に許容値の範囲を定義する一連の制限 $X = \左\ {g_i \左（x \右）\ leq 0、i = 1、...、s \右\}$ 議論 $x \ in X$ 最適化された機能。

したがって、この問題の本質は次のように説明できます。目的関数の最小/最大値を提供するベクトルを検索領域で見つける必要があります。

この問題を解決するための膨大な数のアルゴリズムがあります。従来、これらは2つのグループに分けることができます。

分析アルゴリズム：
- タスクのコンポーネントに制限を課すことができるという事実に関連して、タスクの範囲が狭くなります。
- より高いレベルのオブジェクトをタスクに導入できます（たとえば、特定の順序の派生物）。
- このような方法の間違いない利点は、ほとんどの場合、特定の精度の結果を確実に取得できることです。
発見的アルゴリズム：
- 計算の保証された特性はありません。得られた解が局所極値の引力の領域でさえ落ちたことを確信することはできません。
- 計算の複雑さは少ないため、実用的な結果を許容時間内に取得するために使用できます（たとえば、分析アルゴリズムを使用して回答を取得する場合、1日かかる可能性のある大きな次元の問題について）。

原則として、ヒューリスティックアルゴリズムは、方向性列挙の方法として認識できます。このグループには、かなり有名な遺伝的アルゴリズム、アニーリングシミュレーションアルゴリズム、さまざまなポピュレーションアルゴリズムがあります。多数のアルゴリズムが非常に簡単に説明されています。すべてのタイプのタスクに同時に適した普遍的なアルゴリズムはありません。凸関数をうまく処理できる人もいれば、レベル線の渓谷構造を持つ関数を扱うことを目的とする人もいます。人生のように-すべてには独自の専門性があります。

使用される抽象化

上記の推論に基づいて、変換とアルゴリズムという 2つの概念を扱う最も簡単な方法は私には思えます。それらについてさらに詳しく説明します。

変換

ほとんどすべてのプロシージャ/関数/アルゴリズムは、ある種の変換と見なすことができるため、このオブジェクトを基本的なものの1つとして操作します。

さまざまなタイプの変換の間に、次の階層が提案されています。

要素についてさらに詳しく見ていきましょう。

不均一な変換は、入力オブジェクトと出力オブジェクトのクラスが異なる可能性がある場合の最も一般的な変換です。
同種変換は、入力オブジェクトと出力オブジェクトのクラスが同じ場合の特定のタイプの異種変換です。
ベクトル関数は、セットAの要素で構成されるベクトルを、同じセットの要素で構成される別のベクトルに変換する変換です。
関数（関数）-ベクトル関数に似ています（出力要素がスカラーになっていることを除いて）。
メトリック（Metric）-オブジェクトを数値と一致させる評価変換。

不均一な変換クラスコード

class InhomogeneousTransformation[A, B](transform: A => B) extends Serializable { def apply(a: A): B = transform(a) def *[C](f: InhomogeneousTransformation[B, C]) = new InhomogeneousTransformation[A, C](x => f(transform(x))) }

2つのメソッドのみが含まれており、そのうちの1つがいくつかの変換の構成を作成する手順を実装していることがわかります（通常とは異なる方法でのみ）。これは、単純な変換からより複雑な変換を作成するために将来必要になります。

均一変換クラスコード

 class HomogeneousTransformation[A](transform: A => A) extends InhomogeneousTransformation[A, A](transform) { }

ここでは、2つの型パラメーターが1つにまとめられました。

ベクトル関数クラスコード

 class VectorFunction[A <: Algebra[A]] (transform: Vector[A] => Vector[A])(implicit converter: Double => A) extends HomogeneousTransformation[Vector[A]](transform) { }

一般化クラスの修正されたパラメーター化があります。現在、このパラメーターは、変換されたベクトルがどのオブジェクトのクラスで構成されるかを決定します。このコード「[A <：Algebra [A]]」によって決定されるクラスに課せられる制限に注意する必要があります。制限は次のように表されます。ベクトルを構成するオブジェクトは基本的な算術演算をサポートする必要があり、おなじみの基本関数（指数関数、三角関数など）の引数として使用できます。詳細なコードは、github'eに投稿されているソースで見ることができます（リンクは作業の最後にあります）。

Functionクラスのコードと、暗黙的に異種変換に変換する方法

 class Function[A <: Algebra[A]] (transform: Vector[A] => A)(implicit converter: Double => A) extends VectorFunction[A](x => Vector("result" -> transform(x))) { def calculate(v: Vector[A]): A = transform(v) } object Function { implicit def createFromInhomogeneousTransformation[A <: Algebra[A]] (transformation: InhomogeneousTransformation[Vector[A], A])(implicit converter: Double => A) = new Function[A](x => transformation(x)) }

メトリッククラスコードと関連する変換

 class Metric[A](transform: A => Real) extends InhomogeneousTransformation[A, Real](transform) { } object Metric { implicit def createFromInhomogeneousTransformation[A](transformation: InhomogeneousTransformation[A, Real]) = new Metric[A](x => transformation(x)) implicit def toFunction (metric: Metric[Vector[Real]])(implicit converter: Double => Real): Function[Real] = new Function[Real](x => metric(x)) }

上記の抽象化は、一見したところ、問題のさらなる定式化に必要となる可能性のある基本的なタイプの変換をカバーしています。

アルゴリズム

アルゴリズムを3つの操作のセットとして定義するのは自然だと思います：初期化、反復部分、終了。アルゴリズムの入力で、いくつかのタスク（Task）が提供されます。初期化中に、アルゴリズムの状態が生成され、反復部分を繰り返すことで修正されます。最後に、終了手順を使用して、アルゴリズムの出力パラメーターのタイプRに対応するオブジェクトが、アルゴリズムの最後の状態から作成されます。

クラスコードアルゴリズム

 trait GeneralAlgorithm[T <: GeneralTask, S <: GeneralState, R] { def initializeRandomly(task: T): S def initializeFromSeed(task: T, seed: S): S final def initialize(task: T, state: Option[S]): S = { state match { case None => initializeRandomly(task) case Some(seed) => initializeFromSeed(task, seed) } } def iterate(task: T, state: S): S def terminate(task: T, state: S): R def prepareFolder(log: Option[String]): Unit = { if (log.isDefined) { val temp = new File(log.get) if (!temp.exists() || !temp.isDirectory()) temp.mkdir() else { if (temp.exists() && temp.isDirectory()) { def prepare(file: File): Unit = if (file.isDirectory()) { file.listFiles.foreach(prepare) file.delete() } else file.delete() prepare(temp) } } } } def logState(log: Option[String], state: S, fileId: Int): Unit = { log match { case Some(fileName) => { val writer = new ObjectOutputStream(new FileOutputStream(s"${fileName}/${fileId}.st")) writer.writeObject(state) writer.close() } case None => () } } final def work(task: T, terminationRule: S => Boolean, seed: Option[S] = None, log: Option[String] = None): R = { prepareFolder(log) var currentState = initialize(task, seed) var id = 0 logState(log, currentState, id) val startTime = System.nanoTime() while (!terminationRule(currentState)) { currentState = iterate(task, currentState) id = id + 1 currentState.id = id currentState.timestamp = 1e-9 * (System.nanoTime() - startTime) logState(log, currentState, id) } terminate(task, currentState) } }

したがって、特定のアルゴリズムを作成するには、前述の3つの手順を再定義する必要があります。

最適化アルゴリズムとは何ですか？

非線形計画問題の前述の説明から、最適化アルゴリズムのタスクが関数と検索領域で構成されていることは明らかです（現時点では、検索領域が多次元平行六面体で指定されている単純なケースに限定しています）。

 case class OptimizationTask[A <: Algebra[A]](f: Function[A], searchArea: Map[String, (Double, Double)]) extends GeneralTask { def apply(v: Vector[A]): A = f.calculate(v) }

通常、最適化アルゴリズムの状態は 、シングルポイント（作業中に1つのベクトルが分析および変更される場合）またはポピュレーション/マルチポイント（作業中に複数のベクトルが分析および変更される場合）のいずれかの形式をとります。

 abstract class OptimizationState[A <: Algebra[A]] extends GeneralState { def getCurrentBest(optimizationTask: OptimizationTask[A])(implicit cmp: Ordering[A]): Vector[A] } class MultiPointOptimizationState[A <: Algebra[A]](points: Seq[Vector[A]]) extends OptimizationState[A] { override def toString: String = { s"ID: ${id}\n" + s"Timestamp: ${timestamp}\n" + points.zipWithIndex.map{ case (point, id) => s"# ${id}\n${point}\n"}.mkString("\n") } override def getCurrentBest(optimizationTask: OptimizationTask[A])(implicit cmp: Ordering[A]): Vector[A] = points.minBy(point => optimizationTask(point)) def apply(id: Int): Vector[A] = points(id) def size: Int = points.size } class OnePointOptimizationState[A <: Algebra[A]](point: Vector[A]) extends MultiPointOptimizationState(points = Seq(point)) { override def getCurrentBest(optimizationTask: OptimizationTask[A])(implicit cmp: Ordering[A]): Vector[A] = point def apply(): Vector[A] = point }

したがって、最適化アルゴリズムは次のコードで記述されます。

 abstract class OptimizationAlgorithm[A <: Algebra[A], S <: OptimizationState[A]] extends GeneralAlgorithm[OptimizationTask[A], S, Vector[A]] { }

K-MeansVS。ランダム検索

さて、約束のプログラムの最初の2つのポイントはカバーされています。3番目のポイントに移るときです。

両方のアルゴリズムはさまざまなソースでよく説明されているため、読者がそれらに対処することは難しくないと思います。代わりに、前述の抽象化に類似点を描きます。

K-Meansアルゴリズム

K-Meansアルゴリズムのタスクは、クラスタリングのポイントのセットおよび必要なクラスターの数として明確に定義できます。

 class Task(val vectors: Seq[Vector[Real]], val numberOfCentroids: Int) extends GeneralTask { def apply(id: Int): Vector[Real] = vectors(id) def size: Int = vectors.size def toOptimizationTask(): (OptimizationTask[Real], InhomogeneousTransformation[Vector[Real], kCentroidsClusterization]) = { val varNames = vectors.head.components.keys.toSeq val values = vectors.flatMap(_.components.toSeq) val searchAreaPerName = varNames.map { name => val accordingValues = values .filter(_._1 == name) .map(_._2.value) (name, (accordingValues.min, accordingValues.max)) } val totalSearchArea = Range(0, numberOfCentroids) .flatMap { centroidId => searchAreaPerName .map { case (varName, area) => (s"${varName}_${centroidId}", area) } }.toMap val varNamesForCentroids = Range(0, numberOfCentroids) .map { centroidId => (centroidId, varNames.map { varName => s"${varName}_${centroidId}" }) } .toMap val splitVector: InhomogeneousTransformation[Vector[Real], Map[Int, Vector[Real]]] = new InhomogeneousTransformation( v => Range(0, numberOfCentroids) .map { centroidId => (centroidId, Vector(v(varNamesForCentroids(centroidId)) .components .map { case (key, value) => (key.dropRight(1 + centroidId.toString.length), value) })) }.toMap) val vectorsToClusterization: InhomogeneousTransformation[Map[Int, Vector[Real]], kCentroidsClusterization] = new InhomogeneousTransformation(v => new kCentroidsClusterization(v)) val clusterizationForMetric: InhomogeneousTransformation[kCentroidsClusterization, (kCentroidsClusterization, Seq[Vector[Real]])] = new InhomogeneousTransformation(clusterization => (clusterization, vectors)) val quality: Metric[Vector[Real]] = splitVector * vectorsToClusterization * clusterizationForMetric * SquareDeviationSumMetric (new OptimizationTask(f = quality, searchArea = totalSearchArea), splitVector * vectorsToClusterization) } }

ここで2行に注意してください。

 val quality: Metric[Vector[Real]] = splitVector * vectorsToClusterization * clusterizationForMetric * SquareDeviationSumMetric (new OptimizationTask(f = quality, searchArea = totalSearchArea), splitVector * vectorsToClusterization)

それらの最初では、変換の構成が構築されます。ベクトルは、重心を記述するベクトルのシステムに分割され、重心はクラスター化されます。クラスター化は、「対応する重心からクラスター点の合計距離」によって推定されます

s u m_{i = 1}^{k} s u m_{x_{j} i n S_{i}} \左 | \左 | x_{j} - m u_{i} \右 | \右 |

$\ sum_ {i = 1} ^ {k} \ sum_ {x_j \ in S_i} \左| \左| x_j- \ mu_i \右| \右|$ 。結果として生じる変換の構成は、最適化問題の目的関数と見なすことができます。

ランダム検索アルゴリズム

ランダム検索アルゴリズムの最も簡単な説明は、 Wikipediaにあります。実装されたバージョンの違いは、現在のバージョンから1つのポイントが生成されるのではなく、複数のポイントが生成され、正規分布の代わりに均一なポイントが使用されることです。

K-Meansアルゴリズムを使用して構築されたクラスター化ツールは、その重心によって一意に決定されます。 K-Meansアルゴリズム自体は、個々のクラスター内のすべてのベクトルの平均として計算される、現在の重心を新しい重心に常に置き換えるものです。したがって、K-Meansアルゴリズムの状態はいつでもベクトルのセットとして表すことができます。

したがって、クラスタリングは、K-Meansアルゴリズムを使用して直接構築するか、最適なクラスタリングを見つける問題を解決して、対応する重心からのクラスターポイントの合計距離の最小値を提供することで構築できます。

次元2、3、5のいくつかの合成データセットを生成します。

データ生成コード

正規分布ランダム変数の生成

 f[mu_, sigma_, N_] := RandomVariate[#, N] & /@ MapThread[NormalDistribution, {mu, sigma}] // Transpose

 Num = 100; sigma = 0.1; data2D = Join[ f[{0.5, 0}, {sigma, sigma}, Num], f[{-0.5, 0}, {sigma, sigma}, Num] ]; ListPlot[data2D] Export[NotebookDirectory[] <> "data2D.csv", data2D, "CSV"];

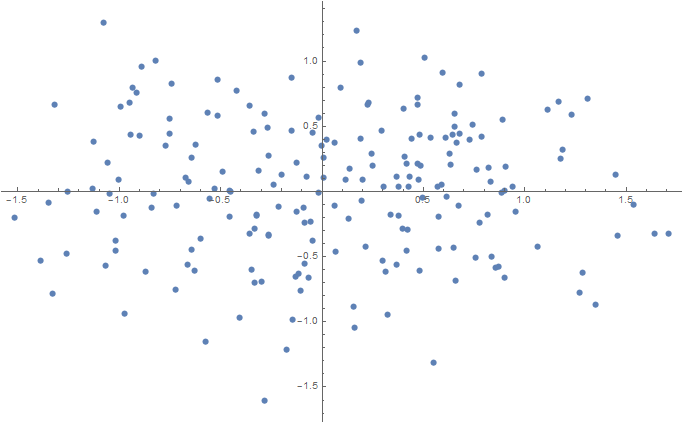
3D（t-SNEを使用した2次元空間への投影）

 Num = 100; mu1 = 0.0; sigma1 = 0.1; mu2 = 2.0; sigma2 = 0.2; mu3 = 5.0; sigma3 = 0.3; data3D = Join[ f[{mu1, mu1, mu1}, {sigma1, sigma1, sigma1}, Num], f[{mu2, mu2, mu2}, {sigma2, sigma2, sigma2}, Num], f[{mu3, mu3, mu3}, {sigma3, sigma3, sigma3}, Num] ]; dimReducer = DimensionReduction[data3D, Method -> "TSNE"]; ListPlot[dimReducer[data3D]] Export[NotebookDirectory[] <> "data3D.csv", data3D, "CSV"];

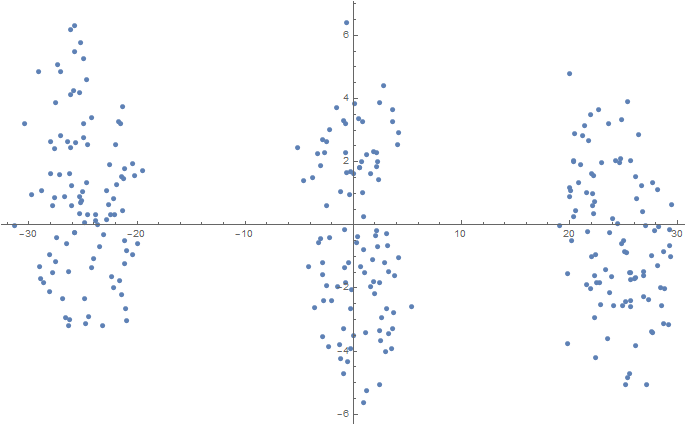
5D（t-SNEを使用した2次元空間への投影）

 Num = 250; mu1 = -2.5; sigma1 = 0.9; mu2 = 0.0; sigma2 = 1.5; mu3 = 2.5; sigma3 = 0.9; data5D = Join[ f[{mu1, mu1, mu1, mu1, mu1}, {sigma1, sigma1, sigma1, sigma1, sigma1}, Num], f[{mu2, mu2, mu2, mu2, mu2}, {sigma2, sigma2, sigma2, sigma2, sigma2}, Num], f[{mu3, mu3, mu3, mu3, mu3}, {sigma3, sigma3, sigma3, sigma3, sigma3}, Num] ]; dimReducer = DimensionReduction[data5D, Method -> "TSNE"]; ListPlot[dimReducer[data5D]] Export[NotebookDirectory[] <> "data5D.csv", data5D, "CSV"];

そして、両方のアルゴリズムを使用してそれらを「駆動」し、クラスター化ツールを構築します。結果は表にまとめられています。

	2D	3D	5D
クラスタリング品質（K-Means経由）：	90.30318857796479	96.48947132305597	1761.3743823022821
クラスター化の品質（最適化による）：	87.42370021528419	96.4552486768293	1760.993575500699

クラスター結果

3D（t-SNEを使用した2次元空間への投影）

5D（t-SNEを使用した2次元空間への投影）

この表は、単純な最適化アルゴリズムでさえ、単純なクラスター化ツールを構築する問題をうまく解決できることを示しています。この場合、作成されたクラスター化ツールは、使用される品質メトリックの観点から最適です（使用される最適化方法はグローバルな最適ポイントの検出を保証しないため、正直、準最適です）。当然、使用される最適化アルゴリズムは、高次元のタスクにはほとんど適していません（さまざまなレベルのいくつかのヒューリスティックに基づいた、より複雑で効率的なアルゴリズムを使用することをお勧めします）。小さな合成問題の場合、ランダム検索はかなりうまくいきました。

あとがきの代わりに

コメントを購読していない記事を読んでくれたすべての人に感謝したいと思います。つまり、この作品の作成に貢献したすべての人。おそらく、このトピックに関する記事が可能な限り表示され、現在のワークロードが表示されることにすぐ注意してください。しかし、今度は、私が始めた問題を終わらせようとすることを言いたいと思います。

参考文献と文献

プロジェクトコード
生成/視覚化のためのコード、
K-means：[ 1 ]、[ 2 ]、[ 3 ]、[ 4 ]
ランダム検索：[ 1 ]、[ 2 ]、[ 3 ]、
Scala：[ 1 ]、[ 2 ]。

非線形計画問題の応用

開発アプローチの定義と主なタスクの定式化

最適化

使用される抽象化

変換

アルゴリズム

K-MeansVS。 ランダム検索

あとがきの代わりに

More articles:

K-MeansVS。ランダム検索