
5月14日、 ロシアコードカップ2017の予選ラウンドが開催されました 。 伝統的に、タスクの分析を投稿して要約します。
A. 小さい数字
B. 新しいキーボード
C. 折りたたみ
D. 鋭い三角形
E. 配列の結合
F. 2つのサブツリー
603人がラウンドに参加しました。各資格ラウンドから最高200人のプログラマーが参加しました。 予選ラウンドの結果によると、55名の参加者が決勝に進みました。
どの参加者も予選ラウンドの6つの問題をすべて解決できませんでした。 15人が5つのタスクを完了しました。 4人、さらに55人の参加者。
3つのベスト:
- そもそも追跡者からかなりの差をつけて(15分間)コストロマのミハイル・イパトフがいた。
- 2位はモスクワのミハイル・ティホミロフが撮影した。
- 3位-サンクトペテルブルクのIgor Pyshkin。
さらに、トップ10ヒット:
- Mitrichev Peter、チューリッヒ、スイス
- Gennady Korotkevich、サンクトペテルブルク、ロシア
- アレクサンダーオスタニン、ドルゴプルドニ、ロシア
- ロシア、サンクトペテルブルク、エルショフ・スタニスラフ
- ジョッキ・ニコラ
- Danilyuk Alexey、オジンツォボ、ロシア
- Du Yuhao、北京、中国
すべての参加者とラウンドランキングテーブルはここで見つけることができます 。
2017年9月に開催される決勝戦に合格したすべての人におめでとうございます。 さて、今-タスクの分析。
A.小さい数字
2秒の制限時間
256 MBのメモリ制限
Boy Vladには2つのお気に入りの数字aとbがあります。 最近、彼は学校で除算と乗算を教えるようになり、すぐに走って好きな数を除算と乗算しました。
最初に、彼はノートに数字aとbを書き、その後、3つの操作のいずれかを順番に実行することを決めました。
- 共通の除数のいずれかで両方の数値を除算します。
- aをその約数gの 1つで割り、 bを g倍します。
- bをその約数gの 1つで除算し、 aをgで乗算します。
各操作の後、彼は古い番号を消去し、2つの結果の番号をノートブックに書き戻し、それらを使用して操作を続行できます。
Vladはまだ小さいので、小さい数字が好きなので、ノートに書かれた数字の合計を最小化しようとします。 彼自身は対処できません。 Vladがこのような操作で取得できる最小数を決定し、最終的に判明する可能性のある数字のペアの例を提供するのを助けてください。
入力形式
入力には、いくつかのテストスイートが含まれます。 最初の行には、テストの数t (1≤t≤500)が含まれています。
各テストの説明は次のとおりです。テストの説明の1行には、 aとbの 2つの数字(1≤a 、 b≤10 9 )-Vladのお気に入りの数字が含まれています。
出力形式
各テストについて、個別の行にそれに対する答えを印刷します-条件から操作を適用することによって取得できる最小量のペア。
複数の回答がある場合は、それらのいずれかを印刷できます。
例
入力データ
2
4 5
4 6
インプリント
1 5
2 3
タスク解析まず、数値aとbを素数に分解します。
ここで、ある素数pが製品abに最初の累乗よりも大きい乗数を入力する場合、すぐに両方の数を数pで除算するか、または数の1つがpで割り切れない場合、因数pを転送することに注意してください別の数、次にpで除算します。
明らかに、製品abにおける素数の出現のパリティは、すべての操作で変化するわけではありません。 次に、すべてを単純なものにします。 番号p 1 、 p 2 、...、 p nがあります。 これらすべての素数の積をd 、d≤abと呼びましょう。 これらの素数は14を超えることはできないと主張されています。1≤a、b≤10 9 、積ab≤10 18 、および最初の15個の素数の積が10 18を超える場合)。 最後の答えは、 xy = dのような数値のペア( x 、 y )であることに注意してください。 その結果、ペアの2番目の要素は最初の要素によって一意に決定されます。 Oのxのすべての可能な除数d (2 n )をソートし、最適なペアを選択します。
B.新しいキーボード
2秒の制限時間
256 MBのメモリ制限
Petyaは新しいキーボードを購入しました。 n個のレイアウトをサポートします。 各レイアウトで、ラテンアルファベットの小文字のサブセットを入力できます。 レイアウトに1からnまでの番号を付けます。
Petyaは、ラテンアルファベットのm個の小文字で構成されるメッセージを入力したいと考えています。 最初のレイアウトは最初はアクティブです。 Petyaは次のことができます。
- レイアウトを切り替えます。 次に、現在のレイアウトの番号がiである場合、新しいレイアウトの番号はi mod n + 1になります。modは剰余剰余演算です。 Petyaが前のアクションによってレイアウトも切り替えた場合、このアクションにはbミリ秒かかります。それ以外の場合、このアクションには1ミリ秒かかります。
- 文字をダイヤルします。 Petyaは、現在のメッセージの最後に、現在のレイアウトの任意の文字を追加できます。 彼はこのアクションにcミリ秒費やします 。
Petyaがメッセージを入力するのに必要な最小時間を決定するのを手伝うか、メッセージを入力することが不可能であることを見つけてください。 メッセージを入力した後に残るレイアウトは任意です。
入力形式
最初の行には、4つの整数n 、 a 、 b 、およびc-キーボードレイアウトの数、およびレイアウトと文字セットの切り替えに必要なミリ秒数が含まれています(1≤n≤2,000、1≤b≤a≤10 9、1 ≤c≤10 9 )。
次のn行には、レイアウトの説明が含まれています。 各レイアウトは、ラテンアルファベットの各小文字がこのレイアウトで入力できる文字のサブセットである、空でない文字列で記述されます。 この行の文字はアルファベット順にソートされています。
最後の行には、行s -Petyaが入力したいメッセージ(行の長さsは 1〜2,000)が含まれています。 文字列sは、小文字のラテン文字で構成されます。
出力形式
単一の整数-メッセージの入力に必要な最小ミリ秒数を出力します。 印刷-メッセージを入力できない場合は1。
例
入力データ
5 3 2 1
abc
d
e
f
def
abcdef
インプリント
15
入力データ
1 1 1 1
a
z
インプリント
-1
タスク解析動的計画法を使用して解決します。 状態はd [i] [j] [k]です。iは前のアクションのタイプを示すフラグです(レイアウトスイッチの場合は0、文字セットの場合は1)、 jは現在のレイアウトの番号、 kは入力された文字数。 値は、この状態に達するのに必要な最小時間です。
kを超えます。 固定kの場合、 jを1からnまで 2回ソートします。 d [0] [j%n + 1] [k] = min(d [0] [j%n + 1] [k]、min(d [0] [j] [k] + b、d [ 1] [j] [k] + a))。 jを1からnまで 2回反復する必要があります。k番目の文字を入力した後、次の文字を入力するレイアウトよりも大きい番号のレイアウトをオンにでき、ループ内のレイアウトを目的のレイアウトに切り替える必要があるためです。 その後、 jを反復処理し、 k + 1の値を更新します。j 番目のレイアウトにメッセージのk番目の文字がある場合、d [1] [j] [k + 1] = min(d [0] [j] [ k]、d [1] [j] [k])+ c。
最後に、答えはmin(d [1] [j] [m])です。ここで、 m = length(s)で 、1からnまでのすべてのj について 。
C.折りたたみ
2秒の制限時間
256 MBのメモリ制限
いつものように、Petyaは数学の授業で退屈したので、ノートのセルを塗りつぶし始めました。 これにうんざりしたとき、彼はkセルの一貫したセルラー図を取得していることに気付きました.2つの塗りつぶされたセルの間には、他の塗りつぶされたセルに沿ったパスがあり、このように隣接するセルには共通の側面があります。
ノートから慎重に切り取り、市松模様のグリッド線(水平または垂直-覚えていない)に沿って半分に折り、ノートの折り畳まれた図のコピーを描きました。 無駄ではありません! ペティアは彼の姿を失い、彼に残されたのは、ノートに描かれた折り畳まれた姿のコピーだけでした。 今、彼は元の形状を復元したいと考えています。
元の図を明確に復元することは常に可能というわけではありませんが、ペティアは、彼が折り畳まれた図を得るために半分に折りたたむことができるkセルの少なくともいくつかの図を描画することで十分だと判断しました。 彼を助けてください-この条件を満たすkセルの初期接続図を見つけてください。
条件からの2番目のテスト例を検討してください。 その中で、折り畳まれた図は文字「P」を表し、元の図は12個のセルで構成されています。 元の図に可能なオプションの1つが図に示されています(曲げは直線y = 3で発生します)。
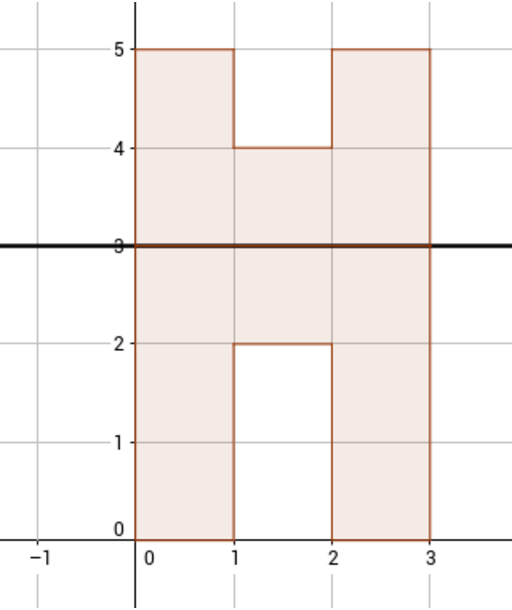
入力形式
入力には、いくつかのテストスイートが含まれます。 最初の行には、テスト数t (1≤t≤200)が含まれています。
次のtテストのそれぞれは、次のように説明されています:テストの説明の最初の行には、2つの整数n 、 k-折り畳まれたVasya図形を構成する塗りつぶされたセルの数と元の図形のセルの数が含まれます(1≤n <k≤10 5 )。
次のn行のそれぞれには、2つの数値x i 、 y iが含まれます-i番目の塗りつぶされたセルの左下隅の座標(-10 10≤x i 、 y i≤10 8 )。 すべての塗りつぶされたセルが異なり、一貫した図を形成することが保証されます。
同じ入力データのすべてのテストの合計kが10 5を超えないことが保証されています。
出力形式
各テストについて、その答えを印刷します。 入力ファイルから図を取得するには、図の説明とそれを曲げる方法を導き出す必要があります。
最初の行に折り畳み線を印刷し、次のk行に2つの整数( x ' i 、 y' i )-接続された図形のセルの座標。入力された図形を取得するために派生した折り畳み線に沿って半分に折り畳むことができます。
折り線は、4つの方法のいずれかで描画する必要があります。
- L num-折り畳みは直線x = numで行われ、左側の部分が右側の上部に重ねられます。
- R num-折り目は直線x = numで作成され、右側が左側の上に重ねられます。
- U num-曲げは直線y = numで行われ、上部が下部の上に重ねられます。
- D num-曲げは直線y = numで行われ、下部は上部の上部に重ねられます。
すべてのx ' i 、 y' i 、および折り目の座標は、絶対値で10 9を超えてはなりません。 そのような図が存在することが保証されます。 適切な回答が複数ある場合は、それらのいずれかを印刷できます。
例
入力データ
2
7 14
0 0
0 1
0 2
1 2
2 2
2 1
2 0
7 12
0 0
0 1
0 2
1 2
2 2
2 1
2 0
インプリント
L 0
0 0
0 1
0 2
1 2
2 0
2 1
2 2
-1 0
-1 1
-1 2
-2 2
-3 2
-3 1
-3 0
U 3
0 0
0 1
0 2
1 2
2 2
2 1
2 0
0 3
1 3
2 3
0 4
2 4
タスク解析折り目は、水平方向に2つ、垂直方向に2つ、正確に4つあることに注意してください。これは、図形が折り目の片側に完全に置かれ、それに触れる必要があるためです。
OX軸に沿った最小座標を持つ折り畳まれた図形のセルのいずれか、つまりセル( x i 、 y i )を取得します。 折り線については、このセルに触れる垂直線x = x iを取ります。 次に、左側で、元の図のk-n個のセルを復元する必要があります。そのため、右側の折り線に沿って左側を重ねた後、入力データから折り畳まれた図を取得します。 k -n≤n(それ以外の場合、曲げた後、 n個以上のセルがあります)から、セル( x i 、 y i )を含む接続された図形を形成する折り畳まれた図形k-nのセルから選択するだけで十分です。 これは、深さを簡単に調べることで実行できます。
D.鋭い三角形
4秒の制限時間
256 MBのメモリ制限
最近では、モスクワの10年生のDmitry Zakharovがd次元空間に点の集合を構築する際に全員を追い抜いて、これらの点に頂点を持つすべての三角形が鋭角になっています。
ターニャはドミトリーで彼女の強さを測定することにしました。 もちろん、彼女はコンピューターを使用する予定です。 まず、彼女は次の問題を解決したいと考えています。 平面上のn個の点を考えると、これらの点に頂点を持つ鋭角三角形の数を見つける必要があります。 すべての角度が厳密に90度未満の場合、三角形は鋭角と呼ばれます。
入力形式
入力には、いくつかのテストスイートが含まれます。 最初の行には、テスト数t (1≤t≤666)が含まれています。
各テストの説明は次のとおりです。テストの説明の最初の行には、数n (3≤n≤2000)-ポイント数が含まれています。
次のn行には、2つの数値x i 、 y i (-10 9≤x、y≤10 9 )-点の座標が含まれます。 1つのテストのすべてのポイントが異なることが保証されています。
同じ入力データのすべてのテストのポイントの総数は2000を超えません。
出力形式
各テストについて、個別の行にそれに対する答えを印刷します-与えられた点に頂点を持つ鋭角三角形の数。
例
入力データ
2
5
1 1
2 2
3 3
4 1
6 4
5
0 0
3 1
5 1
5 -1
1 3
インプリント
3
4
タスク解析鋭角の三角形を計算するには、三角形の総数から直角および鈍角の三角形の数を引くだけで十分です。 1本の直線上の3つの点を、縮退した鈍角の三角形と見なします。
特定のポイントで頂点を使用して構築できる三角形の総数は、 C n 3です。
注:直角三角形と鈍角三角形の数は、与えられた点に頂点をもつ直角三角形と鈍角の数に等しくなります。
与えられたポイントで頂点を使用して、少なくとも90度の角度の数を計算します。 コーナーポイントをループし、指定されたポイントに対する角度で他のすべてのポイントをソートします。 2つのポインターメソッドを使用します。 角度を形成する2番目のポイントをソートします。 適切な3番目のポイントの数を数えるには、他の2つのポイントと少なくとも90度の角度をなすすべてのポイントがソートされた順序でライン上にあり、ラインは角度の増加に向かってのみ移動することに注意してください。
ソリューションの実行時間: O(n 2 log(n)) 。
E.配列の結合
4秒の制限時間
256 MBのメモリ制限
自然数の2つの配列A = [ a 1 、 a 2 、...、 a n ]およびB = [ b 1 、 b 2 、...、 b m ]を考えます。 それらを長さkの辞書式に最小の数Rの配列のk和集合と呼びます。これは2つの空でないサブシーケンスに分割されます。最初のサブシーケンスは配列Aのサブシーケンスで、2番目は配列Bのサブシーケンスです
正式には、辞書の最小配列R = [ r 1 、 r 2 、...、 r k ]を見つける必要があります。この配列には、空でないインデックスセット1≤i 1、1 < i 1、2 <... < i 1、元の配列のt≤nおよび1 < j 1、1 < j 1、2 <... < j 1、 k - t≤m、およびインデックスセット1≤i 2、1 < i 2、2 <.. 。< i 2、 t≤kおよび1≤j 2、1 < j 2、1 <... < j 2、 k - t≤k。
- 1≤p≤t、 1≤q≤k - t 、 i 2、 p ≠ j 2、 qの場合 、
- 1≤p≤tの場合、 a i 1、 p = r i 1、 p ;
- 1≤p≤k- t 、 b j 1、 p = r j 1、 pの場合
たとえば、 A = [1、2、1、3、1、2、1]、 B = [1、2、3、1]、 k = 9の場合、 kの統合はR = [1、1 、1、1、2、1、2、3、1](最初の配列のサブシーケンスは[1、1、1、2、2、1]、2番目の配列のサブシーケンスは[1、2、3、1])。
与えられた2つの配列AとB 、および数kから 、それらのk統一Rを見つけます。
入力形式
入力の最初の行には、数n-配列Aのサイズ(1≤n≤3000)が含まれます。
2行目には、 n個の数値a i-配列A (1≤a i≤3000)が含まれます。
3行目には、数値m-配列Bのサイズ(1≤m≤3000)が含まれます。
4行目には、 m個の数値b i - Bの配列(1≤b i≤3000)が含まれます。
最後の行には数値k (2≤k≤n + m )が含まれています。
出力形式
入力ファイルで指定された配列のk和集合を出力します。
例
入力データ
7
1 2 1 3 1 2 1
4
1 2 3 1
9
インプリント
1 1 1 1 2 1 2 3 1
タスク解析この問題に対する2つの解決策を示します。O(k 2 •log(k))とO(k 2 )です。
Oの解決策(k 2 •log(k))
問題の解決策を3つのポイントに分けます。
- 各配列X ( AまたはB )および各長さ 1≤length≤| X | find minSubsequenceX [length] - 長さlengthの辞書式に最小のサブシーケンスX。
- 最初の配列のサブシーケンスの長さをソートします-1≤t≤min( k -1、| A |)。 1≤k-t≤ | B |の場合、 minSubsequence A [t]とminSubsequence B [k-t]を使用し 、それらを結合する必要があります。
- 2つのサブシーケンスを1つに結合して、長さkの辞書式に最小のサブシーケンスを取得し、回答を更新します。
各長 さのminSubsequence X [長さ]を見つけるには、次のようにします。
- next [i] [c]をカウントします。これは、文字cの次の出現をiの後のXに格納します。
- firstSymbol [length] [i] -配列Xの辞書式に最小のサブシーケンスの最初の文字を計算します[ i .. | X | -1] 長さ 。 これを行うには、次のことに注意してください。
- j 1 = next [i] [1]が存在する場合、 firstSymbol [1] [i] 、 firstSymbol [2] [i] 、... firstSymbol [| X | -j 1 ] [i] 1で始まります。
- j 2 = next [i] [2]が存在する場合、 firstSymbol [| X | -j 1 + 1] [i] 、...、firstSymbol [| X | -j 2 ] [i] 2で始まる。
- ...
- j |アルファベット| =次[i] [|アルファベット| 存在する場合、 firstSymbol [max(| X |-j 1 、| X |-j 2 、...、| X |-j | alphabet |-1 )+ 1] [i]、...、firstSymbol [| X | -j |アルファベット| ] [i]で始まる|アルファベット| 。
ここで、 アルファベットは配列Xの最大数です。
- firstSymbol [length] [i]をカウントすることにより 、各長さの辞書編集的に最小のサブシーケンスXを1文字ずつ繰り返し復元できます。
この項目はO(| X | 2 )に対して機能します。
2つの辞書編集的に最小のサブシーケンスS AおよびS Bが見つかったので、それらを長さkの 1つの辞書編集的に最小のサブシーケンスに結合する必要があります。 2つのポインターp 1およびp 2を使用してサブシーケンスに沿って移動します。 S Ap 1 ≠ S Bp 2の場合、ポインターを小さい数字に移動します。 S Ap 1 = S Bp 2の場合、バイナリ検索により最大共通プレフィックスS A [p 1 .. | S A |]およびS B [p 2 .. | S B |]を見つけ、以下の数値を比較します。 ハッシュを使用して、サブセグメントS AとS Bを比較できます。
この項目はO((| S A | + | S B |)•log(max(| S A |、| S B |)))= O(k•log(k))に対して機能します。
合計で、3つすべてのポイントを合計すると、漸近線O(| A | 2 + | B | 2 + k 2 •log(k))= O(k 2 •log(k))が得られます。
Oのソリューション(k 2 )
配列Aをゼロ、配列Bを最初と呼びます。 1つの要素で答えを構築します。 また、補助値dp [i] [j]もサポートします。ここで、 iは配列の番号(0または1)、 jはこの配列のインデックスです。 dp [i] [j]は配列1- iの最小インデックスに等しく、配列iのインデックスjで停止すると、そこから答えを構築し続けることができます。
回答を構成するk回の反復で、回答に追加することでシーケンスが完了する、つまり、残りの要素が少なくともk - t -1になるような最小要素を見つけます。また、両方のサブシーケンスを考慮する必要があります答えが構築される配列は空ではない必要があります。
O(| A | + | B |)に応答して見つかった要素vを追加した後、 dpの値を更新します。 これを行うには、前のソリューションで計算された次の配列を使用します。
F. 2つのサブツリー
4秒の制限時間
256 MBのメモリ制限
中断されたツリーを検討してください。 vから距離kにある少なくとも1つの頂点をサブツリーに持つ頂点vを考えます。 vからの距離がkより大きいすべての頂点を削除することにより 、頂点vのkサブツリーを頂点vのサブツリーから取得したツリーと呼びます。 たとえば、次の図では、頂点3の2サブツリーが赤でマークされています。

最初の頂点に番号を付け直して2番目のツリーを取得できる場合、2つのツリーを同じと呼びますが、頂点での子の順序を変更することはできません。 たとえば、次の2つのツリーは同じではありません。
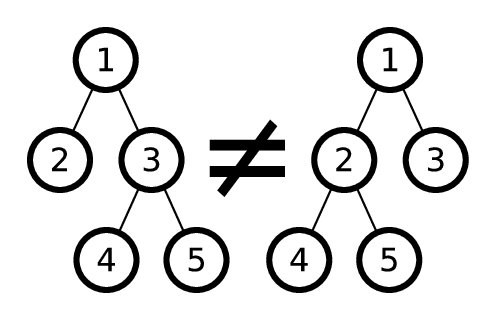
中断された木を考える。 根が異なる2つの同一のkツリーを持つように、最大のkを決定する必要があります。 これらのサブツリーは交差する場合があります。
図は、例のツリーを示しています。
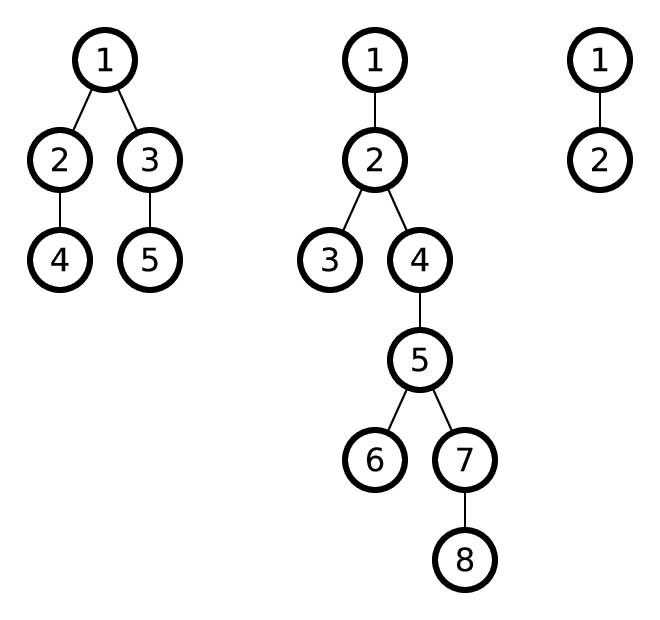
最初の例では、同一の1サブツリーのルートは頂点2と3です。
2番目の例では、同一の3サブツリーのルートは頂点1と4です。
3番目の例では、同じ0サブツリーのルートは頂点1と2です。
入力形式
最初の行には、数t-テストの数(1≤t≤10 4 )が含まれます。
各tテストは次のように説明されます。最初の行には、数値n-頂点の数(2≤n≤10 5 )が含まれます。
これにn行が続きます。 それらのi番目には、番号cnt i-頂点iの子の数、そしてcnt i番号-頂点iの子の数が含まれます。 頂点には1から番号が付けられます。 ツリーのルートは頂点1です。指定されたグラフがルート1のツリーであることが保証されます。
1つの入力のすべてのテストの合計nは2・10 5を超えません。
出力形式
各テストケースについて、異なるルートを持つ2つの同一のkサブツリーが存在するように、最大kを個別の行に出力します。
例
入力データ
3
5
2 2 3
1 4
1 5
0
0
8
1 2
2 3 4
0
1 5
2 6 7
0
1 8
0
2
1 2
0
インプリント
1
3
0
タスク解析仮説により、 k -treeには深さkに必然的にピークがあります。 この要件を一時的にキャンセルします。
いくつかのkのすべてのk木を考えます。 それらは等価クラスに分類できます。 各頂点にc k [v]を関連付けます 。これは、そのkツリーが属する等価クラスのラベルです。
k = 0の場合、頂点の0サブツリーはそれ自体であるため、すべてのc 0 [v]は等しくなります。
k = 1の場合、 c 1 [v]はピークの子の数に等しくなります。
配列c k [v]およびc m [v]から学習して、配列c k + m [v] を構築します。 まず、各頂点vに配列arr k + m [v]を割り当てます。これは、そのk + m-サブツリーの等価クラスを一意に指定します。 u 1 、...、 u sを、走査順序dfsで距離kにある頂点vの子孫とします。 次に、頂点vを配列arr k + m [v] = c k [v]、c m [u 1 ]、...、c m [u s ]に関連付けます。 つまり、 k + m-頂点のサブツリーは、頂点のkツリーとkツリーの下部のmツリーによって定義されます。 以下は、 k = 3およびm = 1の図です。
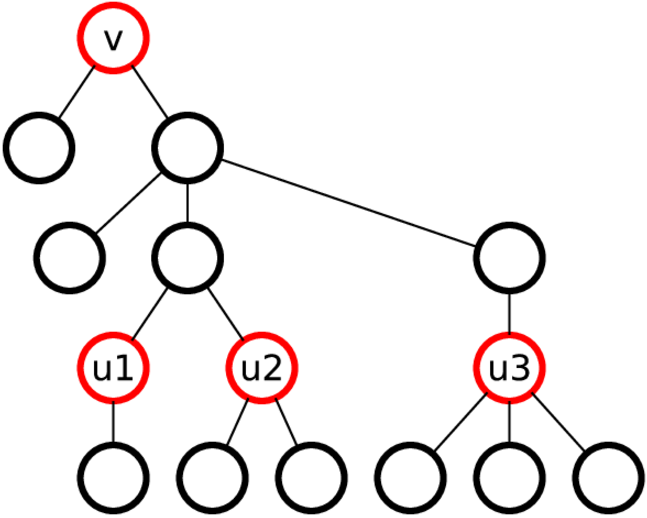
各頂点の距離kで子孫のリストを取得するには、ルートから深さで検索を実行します。 スタックのルートへのパスをサポートし、各頂点をその祖先の配列に距離kで配置します。
arr k + m [v]配列を数値c k + m [v]に変換するには、配列をハッシュし、配列から番号にホウ素またはunordered_mapを使用します。 各頂点はarrリストに一度しか表示されないため、実行時間はO(n)になります。
配列c k [v]が与えられた場合、2つの同一のkサブツリーがあることを簡単に確認できます。 これを行うために、同じc kの 2つの頂点を見つけ、そこから距離kの子孫を持つ頂点のみを見つけます(これは最初にキャンセルした要件です)。
最大kを見つけるために、 c 1 [v]、c 2 [v]、...、c 2 t [v]を計算します (2 tはnを超えない2の最大電力です)。 その後、 kのバイナリ上昇のアナログを使用します。k = 0から始めて、2 t 、2 t -1 、...、2 0を追加しようとします。
ソリューション実行時間: O(nlog(n)) 。
今後の計画
最終ラウンドは9月に行われることを忘れないでください。 その後、タスクの条件とその分析もレイアウトします。 あなたはファイナリストの立場に自分自身を感じ、筋金入りの問題を解決できます。
そして最後に、アイデアの1つを共有します。おそらく来年、「言語のベスト」のような特別なノミネートを行います。 次に、たとえば、最高のC ++ソリューションの所有者が別の賞を受賞します。 何て言うの?