「まあ、戦いなしで? バレーボールはとてもバレーボールです!」
まあ、USB-だからUSB
 KDPVリーダーを甘やかすことは私のルールではありませんが、抵抗することはできませんでした。
KDPVリーダーを甘やかすことは私のルールではありませんが、抵抗することはできませんでした。しかし、約束どおり、MKのタイムサービスから始めます。 このサービスに関連する問題を検討してください-数字のセットがあり、それらの中には、他の所定の数字を超えない数字を強調する価値があります。 時間に移ると、現在の時間(T)が間隔(C)の基準点よりも大きい間隔(I)になる瞬間を判断する必要があると言えます。
この問題をどのように解決でき、ウロボロスはそれと何をしなければなりませんか?
まず、現在の瞬間を特徴付ける数値Tを取得できる必要があります(時間との関係を理解しておくと便利ですが、これは必要ではありませんが、作業を開始するには、数値のサイズと時間の増加に伴うこの数値の動作を知るだけで十分です-増減します) ) 次に、変数Cの現在のTを覚えておく必要があります(同じタイプであることが必要です。そのため、サイズを知る必要があります)。 次に、目的の間隔を特定の数のAndに関連付けることができなければならず(そして、ここでは数Tの正確な動作の知識が必要です)、次の形式で実行することで簡単な比較操作を実行できます。
T = C + I
-この平等が満たされるとすぐに、必要な瞬間に到達しました。
すべてがうまくいきますが、スリッページの問題があります-私たちの行動に関係なく時間の流れ、T変数は同時に変化し、何らかの理由で平等時に比較を実行しないと、条件は失われ、必要なものは決してわかりません私たちにとっては時が来ました(実際、現実の世界では私たちが知るでしょうが、それについては後で詳しく説明します)。 したがって、ハード条件=をsoft> =または<=で置き換える必要があります。変数Tが時間とともに減少し、条件T> = C + Iが得られた場合、これは既に見逃すのがはるかに難しく(可能な場合)、すべてがうまくいくことがわかりません。ポストの残りがどのように満たされるか。
実際、このソリューションには落とし穴がありますが、すぐに気付かないように落とし穴です。 そのうちの1つを考えてみましょう。非常に多くの人がすでに不注意な船乗りを襲っています。 そして、この石は、制限ビット深度またはオーバーフローと呼ばれます。
この問題は、時間が無限であり、MKの数値のビット深度が制限されているために発生します。基本的に、カウントできないセットをカウント可能なセットにプルすることはできません。これは公理です。 したがって、数Tは、サイズに関係なく、特定の時点を一意に決定することはできませんが、期間があります。 この期間の期間は、T + 1で減少する最大数に、Tが1だけ増加する時間を掛けたPr =(Max + 1)* Toです。 たとえば、Tがマイクロ秒ごとに1ずつ増加し、Tの幅が32ビットの場合、周期は(2 ^ 32)*1-6= 4 *(2 ^ 10)^ 3 *1-6〜4 * 10 ^ 3 ^ 3 * 1e-6 = 4 * 10 ^(9-6)= 4000秒、これは1時間強です。 Tがミリ秒ごとに1ずつ増加すると、期間は1000倍になり、4e6秒、つまり約46日間になります。 もちろん、2番目の値は最初の値よりもはるかに大きくなりますが、どちらも永遠に比べてフェードします。
そして、私たちの数が最大値に達したときに何が起こるか-さまざまなオプションが可能です:「横になって」変化しないままにすることができます(しかし、時間の流れの継続を修正する能力を失います)、減少し始めることができます(振り子の仕事をシミュレートしますが、ここでは計算の複雑さ)と最小値を取ることができ、通常はゼロです(後者の現象はオーバーフローと呼ばれます)。
この現象が発生するまでの時間間隔をどのように増やすことができますか?要因のいずれかを増やす必要がありますが、最初の要素を増やすと数Tの操作が複雑になり、2番目の要素を増やすと最小ステップよりも短い間隔で作業することができなくなります。 したがって、ステップとビット深度の選択は常に妥協であり、MKの要件を過大評価せず、作業の利便性を低下させないようにします。
期間を延長する別の方法があります-時間と数Tの間の関係を非線形にするために、ユニティまたは対数より小さい指数を持つべき関数(その区分的線形近似)が最適です(MKで非常に簡単に実装されます)が、このオプションはもっと増分ステップとそれに応じて精度が時間とともに増加するため、実際のソリューションではなく理論上の関心があり、これは受け入れられません。
Tの値の周期性とそれに関連するオーバーフロー(ラップアラウンド、リカウント、リロール、ワープ)で私たちを脅かすもの-Tの挙動の単調性が侵害されているという事実によって、つまり、次の瞬間は前のものよりも大きくない数字で表すことができます(Tがある場合)時間が経つにつれて大きくなります)、より小さくなり、したがって、式は機能しなくなり、この症状は非常に不快になります-プログラムは、予想よりも大幅に短い時間間隔を形成します。
何が起こっているのかを理解するために心に留めておくべき図面を以下に示します。
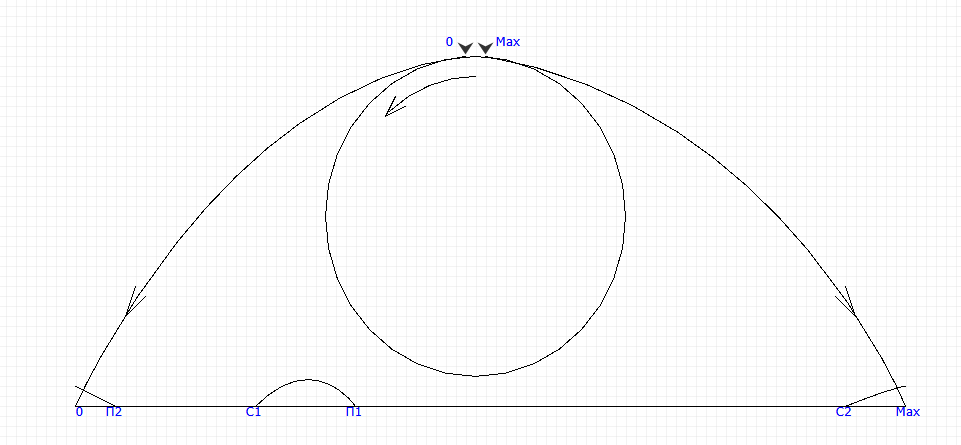
この例を考えてみましょう。簡潔にするために、Tがバイトに配置され、その最大値が255であると仮定します。間隔C = 20および間隔I = 08の形成の初期時間は、式に従って、瞬間28から始まりますこれは正しいですが、C = 250の場合、すでにT = 251で、条件251> =(250 + 8)= 258-256 = 2が満たされますが、これは明らかに期待を満たしていません。 これはあまり頻繁に行われず、期間の終わり近くに起こります。デバイスがそれほど長時間動作しないことが確実な場合は、この機能を無視して、以前に提案された式を使用して時間間隔を追跡できます。これは多くの図書館の著者が行います。 私は2つの理由でこのような慣行に断固として反対しています。まず、悪い習慣がないように常にプログラムを正しく行う必要があります。次に、正しく行うことは難しくありません。
正しい(いずれの場合でも真)数式を取得するには、元のT> = C +に単純な変換を適用し、両側からCを減算し、新しい条件T-C> = Iを取得する必要があります。数学の観点から、これらの条件は同等ですが、数学は無限の幅を持つ理想的な数ですが、無力ではありませんが、境界のある数の場合は、適切な条件を課すだけで済みます。 したがって、これらの条件が与えられた場合、新しい数式は常に正しく機能します。 もちろん、TがCよりも大きい場合にも当てはまりますが、TがCよりも小さい場合にも機能します。これは、減算の顕著な特性により発生します。 Tを次の形式で表します
T = C + D、ここでDは開始に関する加算であり、この加算のプロセスでオーバーフローが発生し、値T = C + DがMax <Cである場合でも、いずれの場合も式は次のようになります。
(C + D)-C = C-C + D = D
つまり、CとTについて探している時間間隔(または、むしろそれを特徴付ける数値)を取得します。このように判明するのは、通常のストリートマジック、つまり、絶対座標系から点Cで始まる相対座標系への遷移です。
元の式の計算の複雑さには1つの加算と1つの比較があり、変更されたものは1つの減算と1つの比較、つまり異なるものではありません(加算、減算、および比較は同じ複雑さです)。 このメソッドの唯一の制限に注意する必要があります-表現可能な最大値以上の間隔を注文することはできません、つまり、注文することはできますが、間隔ははるかに小さくなり、これは明らかですが、非常に悪いです。 また、それほど明白ではない別の制限-可能な限り最大に近い間隔を注文すると、条件が満たされるコントロールポイントが非常に少なくなり、それらをスキップすると、2番目のラウンドに進みます。 しかし、この場合でも、少なくとも注文したものを受け取ることが保証されています。これは何もしないよりもはるかに優れています。
そのため、時間間隔をカウントするための絶対に正しい方法を作成しました。これはあらゆる状況で機能します(もちろん、示された制限を考慮に入れます)が、ご存知のように、完璧に制限はありません。 このメソッドに含まれるリソースを詳しく見てみましょう。2つの変数を覚えて、加算などの2つの操作を実行する必要があります。 リソース要件を削減するには、元の式に戻す必要があります
T> = C + AND
そして、右側の両方の量が区間形成の開始時点で既知であり、遅延の終了時点を計算できることに注意してください
P = C + I、
数式は式になります
T> =P。
残念ながら、その主な欠点-オーバーフロー中の誤操作は有効なままですが、テスト済みの方法で減算T-P> = 0を使用できます。
残念ながら、通常のストリートマジックは私たちを失望させました(fakirは酔ってトリックは失敗しました)。なぜなら、任意の2つの数字の差は0からMaxまでの数字であり、常にゼロ以上ではないためです。 実際、結果は予測可能です。2つの任意の数について、「完全に」不可能という単語からどちらが先行するかを決定することは完全に不可能だからです。
追加の基準を作成して、(T-P)<(P-T)の場合、TがPに先行すると仮定します。 最初は悪くありませんが、この式を使用した直接計算には3つの減算が必要です。これを減らします。 まず、(T-P)+(P-T)= 0 = Max + 1という議論の余地のない事実を確立します。
この明らかな事実から、T-は-->>より大きい場合にのみ-->> =(最大+ 1)/ 2であると推定できます。 2番目の式は明らかに定数であり、コンパイル段階で計算されるため、結果の条件-> =(Max + 1)/ 2は2つの減算演算のみを必要とし、すでに1つのストレージユニットだけメモリを削減していますが、さらに先へ進むことができます。
最後の条件を満たすためには、結果の上位ビットを設定する必要があり、結果ビットの値に応じて条件付きジャンプコマンドを使用できますが、すべてのMKにあるわけではなく、トランスレーターはそれらを十分に使用できないことに注意してください。 幸いなことに、高位ビットを使用するために、MKにはそのようなコマンドがあり、トランスレーターはそれらを非常にうまく実装します-数値の符号をチェックするためのコマンド。 実際、結果を追加コードの数値と見なすと、符号は上位ビットでエンコードされ、数値の上位ビットに1が含まれていること、およびその数値が負であることが一致することを確認します。 したがって、比較条件はT-P <0と記述できます。
符号なしの数値を使用して減算演算を実行し、比較演算中に結果を符号付きの数値として解釈するだけであることに注意してください。 この状況を考慮する必要があるのは、このアルゴリズムを実装するプログラムコードを作成するときです。たとえば、言語Cの場合、対応するフラグメントは次のように実行できます。
if ( (long) ( - ) < 0) ....したがって、1つの数値(P)のみを覚えておく必要があり、チェックの計算の複雑さは1つの減算演算です(比較ではその結果が使用され、追加の演算は不要です)、より良い指標を達成することはほとんど不可能です。 そのような美しさのために支払わなければならなかったもの-現在、最大可能数の半分以上の間隔を注文することはできません。むしろ、注文することはできますが、すぐに停止するので、この制限に勝つかどうかを決定します。 Linuxシステムでは、後者のオプションが採用され、詳細がマクロの背後に隠されているという事実は、構文上の砂糖です。
さて、結論として、少し側に-私は最近、C言語コンパイラ(少なくともそれらのいくつか)の動作が個人的に論理的に呼び出せないことを最近発見しました(実際にはずっと前に忘れていました)。 たとえば、次のコードフラグメントは、私が望むようにはまったく動作しません。
typedef unsigned char Timet;
Timet S = 0xF8, I = 12, T = S + I + 2;
// , MISRA, , , ,
if ( (T - S) >= I) printf ( "time"); //
register Timet D = (T - S);
if (D >= I) printf ("time"); //この形式では時間の有効期限に関するメッセージが1つしか表示されず、Timetのタイプをunsigned longに変更すると、2つのメッセージが表示される理由は完全に理解できません。 それは、もちろん、私は不誠実です、私はこれが起こる理由を理解し、コンパイラを実装するときにそのような決定がなされた理由を理解していません。 しかし、ちなみに、この問題は実際に非常に簡単に解決されます-MISRAサポート(ルール10.1.b)をオンにして、失敗した文字列の使用を禁止すると、すべてを正しく行う必要があります、つまり、確実に、中間の割り当てを記述するよう強制されます。 さらに、この割り当てには何もかかりません。優れたコンパイラーは非常に効率的なコードを作成します。 はい、これは松葉杖です、「しかしそれは動作します」、残念ながら、他の解決策はありません。
次のコードの断片はもっと面白く見えると言わなければなりません
if ( (c = uc ) == uc) printf ( "is equal");実行中、uc変数の一部の値について、予想される同等のメッセージはまったく正当に受信されず、「最も恐ろしいもの、警告のない
自転車 」は受信されません。 そして、私はこれらの2バイトが等しくないことを言う必要はありません-それらは等しく、これは状況の全体の恐怖です。