赤黒の木：短く明確

人生の物語。 少女は彼女のボーイフレンドプログラマーを心理テストに招待しました。

少女：木を描きます。
プログラマー：（二分木を描く）
少女：いいえ、別です。
プログラマー：赤黒の木を描くことができます。

ですから、今日は赤黒木について少しお話したいと思います。 赤黒木に要素を挿入/削除する際のバランス調整アルゴリズムを考慮せずに、ストーリーは短くなります。


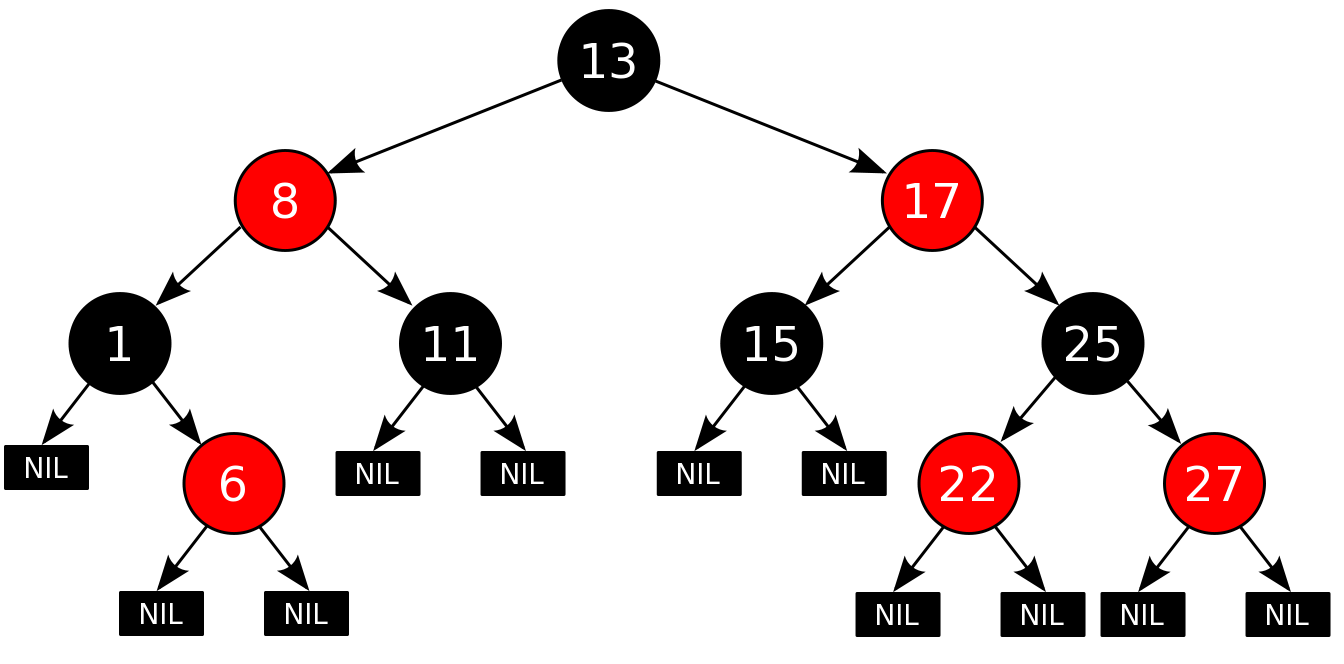
赤と黒の木はバランスの取れた二分探索木です。

バイナリツリーと同様に、赤黒には次のプロパティがあります。

1）両方のサブツリーはバイナリ検索ツリーです。

2）キーを持つ各ノード $$$k$順序付け基準が満たされている：

すべての左の子孫のキー<= $$$k$<すべての子孫のキー

（他の定義では、複製は右側に配置するか、まったく配置しないでください）。
この不等式は、子ノードだけでなく、ノードのすべての子孫についても真でなければなりません。

赤黒木のプロパティ：

1）各ノードの色は赤または黒です（ノードのデータ構造に追加のフィールドが表示されます-少しの色）。

2）根は黒く塗られています。

3）葉（いわゆるNULLノード）は黒く塗られています。

4）各赤いノードには、2つの黒い子ノードが必要です。 黒のノードには黒の子ノードがある場合があることに注意してください。 子としての赤いノードは、黒いノードのみを持つことができます。

5）ノードからリーフへのパスには、同じ数の黒いノードが含まれている必要があります（これは黒い高さです）。

さて、なぜそのような木はバランスが取れているのでしょうか？

実際、赤黒木は、 AVL木のように、厳密なバランスを保証しません（ノードの2つのサブツリーの高さの差が1を超えてはなりません）。 しかし、赤黒木の特性に準拠しているため、時間内に挿入、削除、選択操作を実行できます $$$O（ログN）$。 そして、これが本当かどうか見てみましょう。

赤黒の木があります。 黒の高さが等しい $$$bh$（黒の高さ）。

ルートノードからリーフノードへのパスに赤のノードの最小数（つまりゼロ）が含まれている場合、このパスは $$$bh$。

パスに赤いノードの最大数が含まれる場合（ $$$bh$特性に応じて $$$4$）、このパスは等しくなります $$$2bh$。

つまり、ルートからリーフへのパスは、半分以下の差しかありません（ $$$h <= 2log（N + 1）$、ここでhはサブツリーの高さです）、これはそのようなツリーでの操作の実行時間に十分です $$$O（ログN）$

挿入はどのように行われますか？

赤黒ツリーへの挿入は、通常のバイナリ検索ツリーのように、要素の挿入から始まります。 NULLリーフの位置に要素が挿入されるのはここだけです。 挿入されたノードは常に赤で表示されます。 次は、赤黒木の特性の保存を確認する手順です $$$1-5$。

新しいノードにはすぐに赤色が割り当てられるため、プロパティ1は違反されません。

プロパティ2は、空のツリーがあり、最初に挿入されたノード（別名ルート）が赤く塗られている場合にのみ違反されます。 ここで単にルートを黒で塗り直すだけで十分です。

また、ノードを追加すると、黒い葉の多いNULLノードを受け取るため、プロパティ3も違反されません。

基本的に、他に2つの違反があります。

1）赤いノードに赤い子ノードがある（プロパティ違反 $$$4$）

2）ツリー内のパスには、異なる数の黒いノードが含まれています（プロパティ違反 $$$5$）

さまざまなケースでの赤黒木材のバランス調整についての詳細を参照してください（プロパティの違反を有効にした場合、5つあります） $$$2$）はwikiで読むことができます 。

一般的にどこかで使用されていますか？

はい！ 3年目に研究所で「アルゴリズムとデータ構造」を読んだとき、赤黒の木がどこかで使われているとは想像できませんでした。 バランスの取れた木のテーマが好きではなかったことを覚えています。 ああ、これらの赤黒の木の親族関係（「おじさん」、「祖父」、「黒の兄弟とゴッドファーザーの赤の父」）、サンタバーバラは直接です。 AVL樹の左右の大小の回転は、連続的なジェットコースターです。 また、あなたは赤黒の木が好きではありませんか？ だから、あなたはそれらを調理する方法を知らないだけです。 そして誰かがそれを拾って調理しました。 そのため、たとえば、ほとんどのライブラリの連想配列は、赤黒木を通じて実装されます。

私が伝えたかったのはそれだけです。