潜在的に危険なアルゴリズム

今日の数学モデルとアルゴリズムは、私たちの日常生活に影響を与える重要な決定を下す責任があり、さらにそれらは私たちの世界を支配しています。

高度な数学がなければ、量子コンピューターで整数を因数分解するためのショアアルゴリズム、素粒子物理学の標準モデルを構築するためのヤンミルズゲージ理論、医療および地球物理トモグラフィーの統合ラドン変換、疫学モデル、保険のリスク分析、確率的価格モデルを失うことになります金融デリバティブ、RSA暗号化、流体の動きと気候全体の変化を予測するためのナビエ・ストークス微分方程式、すべて工学 自動制御の理論から、最適な解決策を見つけるための方法や、考えもしなかった他の何百ものものまでの開発。

数学は文明の中心です。 この基礎の誕生からエラーが含まれていることを知るのは、さらに興味深いことです。 何千年もの間、数学の誤りは目に見えないままであることがあります。 時々、それらは自然に発生し、すぐに広がり、コードに侵入します。 方程式のタイプミスは災害につながりますが、方程式自体は潜在的に危険です。

私たちは間違いを異質なものと認識していますが、私たちの生活がその周りにあるとしたらどうでしょうか？

証拠を証明する方法

Beauty SquaredのAlex Bellosは、4色の定理の例によって、コンピューターと数学がまったく信頼できるかどうかを議論します。 この定理は、球体上にあるマップは4色以下の色（ペイント）で色付けできるため、境界の共通セクションを持つ2つの領域は異なる色でペイントできると主張しています。 この場合、領域は単純に接続することも多重接続することもできます（「穴」が存在する可能性があります）。境界の共通セクションは線の一部を意味します。つまり、1つのポイントでのいくつかの領域のジョイントは共通の境界とは見なされません。 この定理は1852年にフランシスガスリーによって定式化され、長い間証明されていませんでした。

1976年、イリノイ大学のケネスアペルとウォルフガングハーケンは、スーパーコンピューターを使用して、可能なすべてのマップ構成を列挙してチェックしました。 証明の最初のステップは、1936年のカードの特定のセットがあったことを証明することでした。それらのいずれにも、定理に反論する小さなカードを含めることはできませんでした。 著者は、1936年の地図のそれぞれについてこの特性を証明しました。 その後、定理に対する最小の反例は存在しないと結論付けられました。そうでなければ、これらの1936年マップのいくつかが含まれているはずでしたが、そうではありません。

長い間、だれもコンピュータの証明を証明できませんでした。すべてを検証するには計算が多すぎました。 「純粋な」数学の観点からは、このような問題を解決することは困難でした-ユークリッド以来使用されていた定理の証明の標準と矛盾していました。 さらに、数学者はプログラムにエラーがあるかもしれないと示唆しました。 そして、実際にはコードにエラーがありました。

2004年、Microsoft Research LabのGeorge Gontierは、独自の関数型プログラミング言語Gallinaを使用して、Coq v7.3.1を使用して証明を再確認しました。 数学者は次の質問をしました。チェッカープログラムにエラーが含まれていないという証拠はありますか？ これには完全な自信はありませんが、プログラムは他の多くのタスクで繰り返しテストされています。 その結果、数学者を支援する特殊なソフトウェアには、数万の正式な証明が含まれています。

すべてのエラーが見つかったにもかかわらず、4色の定理の証明は数学で最も徹底的にテストされたものの1つです。

乱数と暗号化

コンピューターは数学を大幅に進歩させることを可能にしましたが、最も重要なことは、外見的には美しいが「役に立たない」定理から商業的に成功する製品を作ることを可能にしました。 コンピューター数学の主な成果の1つは、乱数ジェネレーターの使用です。

乱数を見つける問題は、Bellosの本 『Land in Numbers』で興味深いことに触れられています。 数学の魔法の世界への並外れた旅。」 数πは、ランダム性の良い例と長い間考えられてきました。 もちろん、無限の数のシーケンスがあります。 したがって、小数点以下17 387 594 880位では、数字の0123456789が一列に並んでいますが、このシーケンスは単なる偶然です-コインを投げる実験が示すように、直観に矛盾する長いシーケンスはより一般的です。

Pi番号はランダムであるかのように動作する場合がありますが、実際には事前に決められています。 たとえば、πの数字がランダムな場合、小数点以下の最初の数字が1になる可能性は10％だけです。 ただし、1が存在することは完全に確実です。 πは偶然ではありません。

実際、周囲の現象のランダム性を見つけることは困難です。 コインが偶然投げられるのは、着陸の正確さを考えていないためだけですが、正確な速度、トスの角度、空気密度、およびプロセスの他のすべての重要な物理的パラメーターを考慮すると、どちらの側に落ちるかを正確に計算できます。

数学を物理の平面に変換することにより、驚くべき結果を達成できます。 1969年、数学者のエドワードソープは、理想的なランダム統計からの系統的偏差を減らすというカジノの要望により、ボールの動きを予測しやすくなることを発見しました（実際、彼はこの問題に10年以上対処していました）。 実際には、ホイールの軸を調整するときに傾斜する場合があります-0.2度の傾斜で十分であるため、漏斗状の表面にボールがホイールにジャンプすることはありません。 この情報を使用して、予想されるペイオフをベットの0.44にすることができます。

数値のランダム性は、とりわけ、すべての古い以前の値の知識に基づいても、この数値の次の値または前の値を推測することが不可能であることを意味します。 これは、十分なエントロピーまたは真にランダムな情報と混合した強力な暗号化の原理に基づいている場合にのみ、疑似乱数ジェネレーター（PRNG）によって実現できます。

純粋な数学に基づいて、非常に高い耐久性を持つPRNGジェネレーターを作成することができます。 たとえば、Blum-Blum-Shubアルゴリズム（Blum coupleアルゴリズムとMichael Shubの著者）は、整数因数分解の想定される複雑さに基づいて高い暗号強度を持っています。 アルゴリズムは数学的に美しいです：

$$

$$X_ {n + 1} = X_ {2} ^ {n} mod M、$$

ここで、M = pqは2つの大きな素数pとqの積です。 アルゴリズムの各ステップで、パリティチェックビットまたは1つ以上の最下位ビットX _nを取得することにより、X _nから出力が取得されます。

一部の数学者は、整数の因数分解は予想されるほど難しくない可能性があり、アルゴリズムの出力は十分な量の計算で識別できる数値になるため、BBSアルゴリズムなどを潜在的に危険だと考えています。 素因数分解に高速量子アルゴリズムを使用すると、暗号化暗号の脆弱性を検索するための膨大な可能性の空間が実現されます。 例のために遠くに行く必要はありません。 かつて強力なDESアルゴリズムは、多くのアプリケーションにとって不十分であると考えられています。 誰もが10億年の計算時間を必要とすると考えていたいくつかの古いアルゴリズム（MD4、MD5、SHA1、DESおよびその他のアルゴリズム）は、今では数時間で解読できます。

Fortunaファミリーの暗号ジェネレーター（FreeBSD、OpenBSD、Mac OS Xなどで使用）では、ジェネレーターは、連続する自然数の暗号化を通じて擬似乱数データを受け取ります。 初期番号が初期キーになり、各要求後にキーが更新されます。アルゴリズムは、古いキーを使用して256ビットの擬似ランダムデータを生成し、結果の値を新しいキーとして使用します。 さらに、カウンターモードのブロック暗号は、周期が2 ^128の非反復16バイトブロックを生成しますが、そのようなシーケンス長の真のランダムデータでは、同じブロック値が同じ値で発生する可能性が高くなります-上記のPi番号の例で見たように。 したがって、統計的特性を改善するために、1つの要求に応じて発行できるデータの最大サイズは2 ²⁰バイトに制限されます（このシーケンスの長さで、真にランダムなストリームで同じブロックを見つける確率は2 ^-97のオーダーです）。 それ以外のすべては、マウスの動き、キーを押す時間、ハードドライブの応答、サウンドカードのノイズなど、本当に（おそらく）ランダムなデータと混同されます。

しかし、そのような乱数のセットであっても、数学者はパターン化されたシーケンスの存在を疑い、放射性崩壊や宇宙放射線などの予測できない物理現象の使用を提案します。

エラーの発生

プログラマが迷惑なバグを認めた場合、すべての保護レベルでは不十分な場合があります。 プログラム作成のいずれかのステップでエラーが発生すると、システム全体のセキュリティが損なわれる可能性があります。

if ((err = SSLHashSHA1.update(...)) != 0) goto fail; goto fail; /* BUG */ if ((err = SSLHashSHA1.final(...)) != 0) goto fail; err = sslRawVerif(...); … fail: … return err; 

2014年の従来のSSL / TLSエラー。 追加のgotoステートメントにより、iOSおよびMacデバイスは無効な証明書を受け入れ、MITM攻撃を受けやすくなります。 開発者が誤って1つの冗長なgotoステートメントを追加しました。おそらくctrl + c / ctrl + vを使用して、SSL / TLS接続のすべての証明書チェックをバイパスできるようにしました。 このエラーは1年以上存在し、その間、数百万のデバイスがMITM攻撃の影響を受けやすくなりました。 皮肉なことに、同じ年に、GnuTLS証明書検証コードでより深刻な「goto」エラーが発見されました。 さらに、エラーは10年以上存在していました。

単純なタイプミスは、予想外に見にくい場合があります。 幸いなことに、これはまさに初期のテストで修正できるエラーです。 ただし、より複雑なエラーの検索には、常に時間がかかります。 最終的には、プログラムは仕様の残りの部分ではなく、テストに合格するようにさらに適合される可能性があります。

数学の観点から見ると、正しい結果を与える正しい方程式でさえ、広範囲にわたる結果をもたらすエラーを含んでいる可能性があります。 このアイデアは、貿易の数学的基礎となり、銀行をいくつかの世界的な危機に導いたブラック・ショールズ方程式によってよく説明されています。 美しい、正しい方程式は、ランダム性という1つのパラメーターのみを考慮しませんでした。

オプション価格設定モデルの式は、1973年にフィッシャーブラックとマイロンショールズによって最初に開発されました。 オプションとは、製品または証券の購入者（いわゆる原資産）が、契約によって決定された時間に所定の価格でこの資産を購入または販売する権利（ただし、義務ではない）を受け取る契約です。

欧州オプションの理論価格を決定するモデルは、原資産が市場で取引される場合、そのオプションの価格は市場自体によって暗黙的に設定されることを暗示しています。 ブラックショールズモデルによると、オプションの価値を決定する際の重要な要素は、原資産の予想されるボラティリティ（価格ボラティリティ）です。 資産の変動に応じて、資産の価格は上下し、オプションの価値に直接比例して影響します。 したがって、オプションの価値がわかれば、市場が期待するボラティリティのレベルを決定できます。

方程式は次のようになります。

$$

$$C（S、t）= SN（d_ {1}）-Ke ^ {-r（Tt）} N（d_ {2}）、\\ d_ {1} = \ frac {ln（S / K）+ （r + \ sigma ^ {2} / 2）（Tt）} {\ sigma \ sqrt {Tt}} \\ d_ {2} = d_ {1}-\ sigma \ sqrt {Tt}$$

C（S、t）-オプションの有効期限が切れる前の時刻tでのオプションの現在の値。
Sは原資産の現在の価格です。
N（x）は、標準正規分布の条件下で偏差が小さくなる確率です（したがって、標準正規分布関数の値の範囲が制限されます）。
Kはオプションの行使価格です。
r-リスクフリー金利;
Tt-オプション期間の満了までの時間（オプション期間）。
σは、原株のボラティリティ（分散の平方根）です。

この方程式は、推奨価格を他の4つの値にリンクします。 次の3つを直接測定できます。時間、オプションが保護される資産の価格、およびリスクのない金利。 4番目の値は、資産のボラティリティです。 これは、市場価値がどれほど変動するかを示す指標です。 方程式は、オプションの期間中、資産のボラティリティが変化しないと仮定していますが、この仮定は誤りです。 ボラティリティは、価格変動の統計分析によって推定できますが、正確で信頼できる方法で測定することはできず、推定値が正しくない場合があります。

このモデルは1900年に遡り、博士論文で、フランスの数学者Louis Bachelierは、ブラウン運動として知られるランダムなプロセスによって株式市場の変動をモデル化できると示唆しました。 各時点で、株価は上昇または下降し、モデルはこれらのイベントの固定確率を仮定します。 それらは、他の人よりも等しく可能性が高いか、より高い可能性があります。 それらの位置は株価に対応し、ランダムに上下します。 ブラウン運動の最も重要な統計的特徴は、その平均と標準偏差です。 平均は、通常、特定の方向に上下に変動する短期の平均価格です。 標準偏差は、標準統計式を使用して計算された平均と価格が異なる平均値と見なすことができます。 株価の場合、これはボラティリティと呼ばれ、価格の変動性を測定します。

Black-Scholes方程式は、さまざまな他の量の変化率に関して価格の変化率を表す偏微分方程式によって、金融契約が始まる前から合理的に評価することを可能にしました。 フォーミュラの問題は、さまざまなケースでの修正の可能性でした。 実際には、銀行はさらに複雑な式を使用しており、そのリスク評価はますます不透明になっています。 企業は数学的に才能のあるアナリストを雇って、同様の公式を開発し、市場の状況が変わっても違いのないソリューションを得ます。

モデルは、ドリフトとボラティリティの両方が一定である裁定価格設定の理論に基づいていました。 この仮定は金融理論では一般的ですが、実際の市場ではそうではないことがよくあります。はい、歯が痛くなった「ブラックスワン」について話しています。 市場のボラティリティの予想外の変化は、フォーミュラの助けでは予測できない結果をもたらしました。 1998年の危機は、ボラティリティの大きな変化が予想よりも頻繁に発生することを示しました。 2008年の危機は、ランダムな計算式を使用した誤ったリスク評価により流動資産が不足したために倒れた銀行の数を示しました。

ブラック・ショールズ方程式の根源は数理物理学にあり、そこでは量は無限に割り切れ、時間は連続的に流れ、変数は滑らかに変化します。 このようなモデルは、実際の生活と互換性がない場合があります。

元のコンピューティングの問題

エラーを予測するには、適切なリスク評価が重要です。 私たちがすべての人類を殺す巨大な小惑星にさらされるリスクを計算する場合、小惑星が実際に人類を2回殺すと言う間違いは問題ではありません。 しかし、ミラーエラー-実際に人類の半分を殺す小惑星-は非常に重要です！

小惑星の飛行を信じられないほど計算した2つのイベントの違いがどこにあるか、第1種のエラー（誤検知）と第2種のエラー（誤検知）は統計的仮説検定の重要な概念です。

最初の種類の間違いは、多くの場合、誤警報、偽陽性、または偽陽性と呼ばれます。たとえば、血液検査で病気の存在が示されましたが、実際には人は健康です。 この場合の「ポジティブ」という言葉は、イベント自体の望ましさや望ましさとは関係ありません。

第1種のエラーの大きさは、次の式で計算できます。

$$

$$P1 = 2 * \ int_ {a} ^ {d} F（x）* dx * \ int _ {-\ infty} ^ {p} F（\ Delta）* d \ Delta、$$

どこで
F（x）は、測定値の分布関数です。
a、dは、第1種のエラーの確率がある区間の境界です。
F（Δ）は、測定器の誤差の実際の値の分布関数です。
-∞、pは、測定器のエラーが第1種のエラーの発生を妨げない区間の境界です。

第2種の間違いは、見逃したイベントまたは偽陰性と呼ばれます-人は病気ですが、血液検査ではこれが示されませんでした。

第2種の誤差の大きさは、次の式で計算されます。

$$

$$P2 = 2 * \ int_ {c} ^ {a} F（x）* dx * \ int_ {p} ^ {+ \ infty} F（\ Delta）* d \ Delta、$$

どこで
c、aは、第2種のエラーが発生する確率がある区間の境界です。
p、+∞は、測定器の誤差が第2種の誤差の発生を妨げない区間の境界です。

数学では、概念は次のように形成されます。

• 定理はまだ真であるが、証明が正しくなかったエラーは、第1種に属します。
• 定理が偽であり、証明も偽である場合のエラーは、第2種に属します。

エラーの発生は、証拠の基準の変更に関連する場合があります。 たとえば、 デイビッド・ヒルバートがユークリッドの証明で誰も気付かなかった誤りを発見したとき、ユークリッド幾何学の定理はまだ有効のままであり、ヒルベルトは形式システムに関して現代の数学者思考であったために誤りが生じました（ユークリッドと考えていませんでした）。 次に、ヒルベルト自身がいくつかの迷惑なミスを犯しました： 数学の23の基本的な問題の有名なリストには、正しい数学的な問題ではない2が含まれています（1つはあまりにも漠然と定式化されており、もう1つは解決されていない、 、数学ではありません）。

他の科学は、人類の歴史を通して続くエラーの数の点で数学と比較することはできません（恐らく声明が大きすぎ、物理学者はこの議論での勝利を支持する多くの議論をするでしょう）。 最も厄介なミスの1つは、無限小数の方程式が存在しないことでした。これは、0と見なされることもあれば、ゼロ以外の無限小数と見なされることもありました。 中世の誤った計算に基づいて、何世紀にもわたって誤って発展した理論が構築されました。

21世紀に祖先やすべての天才とは根本的に異なる人々が例外なく生まれ始めたとは考えにくい。 しかし、最も賢いのは私たちであり、私たちが発明したのは世界の真の姿だと思われます。 しかし、例えば、ユークリッドは、論理に基づいて、彼の同時代人が欠陥を見つけることができなかった科学的構造を作成しました。 同様に、数学ツールに欠陥が見られない場合もあります。

説得力のある証拠は、数学雑誌に掲載されているすべての記事の3分の1にエラーが含まれていることを示唆しています。 そして、数学の後、プログラミングの問題の存在を認識すべきです。 Microsoft DOSコードの4000行から、Windowsの後続バージョンで数千万行に切り替えると、アクティブなエラーの数が比例して増加するという冗談があります（ある程度真実があります）。

プログラムにはエラーが含まれるだけでなく、数学者にエラーがないかどうかをチェックする数学プログラムも含まれます。 この一般的な問題は、他の検証システムの自動検証システムの作成につながります。 たとえば、整数のエントリを持つ行列の行列式を計算するときに、人気のあるMathematicaシステムでどのようにエラーを見つけたかを見ることができます。 Mathematicaは行列の行列式を誤って計算するだけでなく、同じ行列式を2回評価すると異なる結果を生成します。

少し前までは、数学者はコンピューターの使用をまったく承認していませんでした。複雑な計算を避ける必要性が常にこの分野の進歩を促し、エレガントで美しいソリューションを生み出しました。 そして今、数学者は、最も人気のあるバリアント（Mathematica、Maple、Magma）のソースコードを閉じた特殊なソフトウェアを使用することに慣れています。

数学者は常に間違っています-これは正常です

コンピュータ業界では、ほとんどの人が考えるよりも数学エラーがはるかに一般的です。 また、気付かれない多くのエラーがあります。

17世紀に特性を研究した数学者のMaren Mersenneにちなんで名付けられたメルセンヌ数は、M _n = 2 ⁿ -1の形式をとります（nは自然数）。 この種の数は、それらのいくつかが素数であるという点で興味深いです。 メルセンヌは、数値2 ⁿ -1がn = 2、3、5、7、13、17、19、31、67、127、257の素数であり、他のすべての正の数値n <257の化合物であると仮定しました。メルセンヌは5つの誤りを犯しました。n= 67と257は複合数を与え、n = 61、89、107は単純な数を与えます。

メルセンヌの理論と反論の間にはほぼ200年が経過しました。
2 ⁶⁷ -1という数字が193 707 721と761 838 257 287の2つの数字の積であることは、1903年にコール教授によって証明されました。 数を因数分解するのにどれだけの時間をかけたかを尋ねられたコールは、「3年間、すべての日曜日」と答えました。

数学者は自分の仕事の重要性を理解することすら間違っています。 数論に携わったケンブリッジ教授G.H.ハーディは、有用な知識が人類の物質的な幸福に影響を与える可能性がある知識として定義されている場合、純粋に知的満足が不可欠ではないため、高等数学のほとんどは役に立たないと主張した。 彼は、純粋な数学の追求を、その完全な「無用」は全体として害を引き起こすために使用できないことを意味するだけであるという議論で正当化します。 ハーディは、数論には実際的な応用がないと述べた。 実際、私たちの時代では、この理論は多くのセキュリティプログラムの根底にあります。

ケルベロスの問題

いくつかの変更を加えたNeedham-Schröderプロトコルに基づくKerberosネットワークプロトコルは、クライアントとサーバー間の接続を確立する前に、クライアントとサーバーの相互認証のメカニズムを提供します。 このプロトコルには複数の保護レベルが含まれており、Kerberosはクライアントとサーバー間の最初の情報交換が安全でない環境で行われ、送信されたパケットを傍受および変更できることを考慮に入れています。

プロトコルの最初のバージョンは、1983年にマサチューセッツ工科大学（MIT）でAthenaプロジェクトの一環として作成されました。その主な目的は、MITの教育プロセスにおけるコンピューターの導入計画を開発することでした。 プロジェクトは教育的なものでしたが、最終的には今日使用されているいくつかのソフトウェア製品（たとえば、 X Window System ）を世界に提供しました。

1989年に、プロトコルの4番目のバージョンが登場し、公開されました。 他の主要な分散システムプロジェクト（ AFSなど）は、認証システムにKerberos 4を使用しています。 Kerberos乱数ジェネレーターは、さまざまな暗号化システムで数年間広く使用されています。 そして10年間、誰もKerberosモジュールを使用するシステムに侵入できる巨大な穴に注意を向けませんでした。

プログラムは膨大な数の配列からキーをランダムに選択する必要があると想定されていましたが、乱数ジェネレーターが小さなセットから選択していることが判明しました。 10年間、研究者はKerberos 4では乱数がまったくランダムではなく、秘密鍵が数秒で取得できることを知りませんでした。

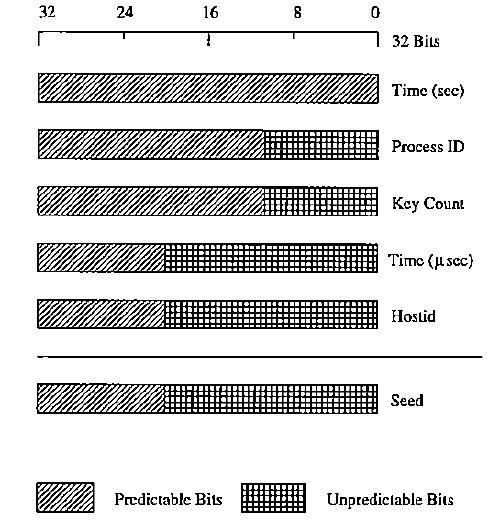
Kerberos 4はUNIX機能を使用して、ランダムな56ビットDESキーを作成しました。 擬似乱数の生成に使用されるアルゴリズムの誤った実装により、キー番号のシーケンスのエントロピーは32ビットのみであり、最初の12ビットはめったに変更されず、予測可能であるという事実に至りました。 その結果、Kerberos 4には約220（または約100万）のキーしかありませんでした。

この話で最もおもしろいのは、Kerberos 4にオープンソースがあることです。 単にオープンソースを使用するだけでは、その正確性に自信が持てないはずです。 残念ながら、公開の精査のために利用可能なコードを持つことは、セキュリティの誤った理解につながりました。 さらに、時間が経つにつれて、その安全性に対する信頼が高まりました。問題がまだ検出されていなければ、起こりうるエラーの可能性が減少するという信念によって強化されました。 通常、リリース後数日でソフトウェアにバグが見つかる開発トレンドは、この一般的な問題を悪化させるだけです。

何も意味しない間違い

間違いは、方程式または証明を破棄しなければならないことをまったく意味しない場合があります。

ディリクレの原理-1834年にドイツの数学者ディリクレによって定式化された有名な声明は、特定の条件下でオブジェクト（「ハト」）とコンテナ（「ケージ」）の間に接続を確立します。

ハトがセルに座っており、ハトの数がセルの数よりも多い場合、少なくとも1つのセルに複数のハトが含まれています。

私たちは数学の言語に翻訳します：

少なくともkn + 1個のハトをn個のセルに配置し、次に少なくともk + 1個のハトをセルの1つに配置します。

おもしろそうに聞こえますが、最もおもしろいのは別の分野です。 数理物理学では、ディリクレの原理は潜在的な理論に関連し、次のように定式化されます。関数u（x）がポアソン方程式の解である場合

Δu + f = 0

境界条件を持つドメインΩ⊂Rnで： Ω の境界上のu = gの場合、 uは変分問題の解として見つけることができます：最小値を見つける

$$

$$E [v（x）] = \ int _ {\ Omega} ^ {}（\ frac {1} {2} | \ bigtriangledown v | ^ {2}-vf）dx$$

境界Ωでv = gとなるようなすべての二重微分可能な関数v

厳密な数学の観点から見たレジューヌ・ディリクレのこのような美しく重要な証拠は誤りであることが判明しました。 彼の死の数年後、数学者カール・ワイエルシュトラスは、この原則が満たされていないことを示しました。 この目的のために、彼は与えられた境界条件の下で積分を最小化する関数を見つけることが不可能である例を構築しました。

, , , .

/

, , . : . , . 2/3 : 0,6666666666666667.

7. Patriot - , 28 100. . 24- . , 1/10, , 24 .

Patriot 100 . 0,34 . 1/10 = 0,0001100110011001100110011001100… 24 0,00011001100110011001100, , 0,0000000000000000000000011001100… 0,000000095 . 0,000000095 × 100 × 60 × 60 × 10 = 0,34 .

1676 , 0,34 , .

:

(-1) ^s × M × B ^E , s — , B — , E — , M — .

, - : c/0 = ±∞ (3/0 = +∞, -3/0 = -∞, 1/∞ = 0), , , . 0/0 , NaN.

- , . FPU , , GPU CPU.

, , , , . . Sun , . 1990 Wilf-Zeilberger , , .

, /, . «» - . -1 « », . , , , . , .

, , . ,

 DO 17 I = 1, 10 

 DO17I = 1.10 

DO17I — .

Sun , , . , , Sun , , - .

« , » . 1973 , 1976 « ». : . , . . .

, . , , , .

. , . , f (x, y) = x * y x y x y. , 70- , : .

. . , , , ?

, ( ). 1990- IBM . , - 256 . , 3,7 × 10 ^-9 1,4 × 10 ^-15 . 1 20 , :

1 – (1 – 1,4,e-15)60 × 20 × 1024² = 1,8e-6

, , , . , , . - , .

1990- « » « », . , , . , , .

(. , , — , . , 21- 100 Foreign Policy . , «» — . , , , , , , , , ).

? .

, — . , : , , 9,8 / ² …

. , 9,780 /² 9,832 /², , , 9,80665 /². 9,8. , 9,8, 9,9 9,7? , 9,80000, 9,80001 9,79999?

, , , .

2008 -330 Qantas 3 , . , .

どうした -330, , (FCPC), - (ADIRU). ADIRU Intel , . . (, , . ).

: , 1,2 . 1 — . , 1,2 . - 0,2 .

, , , . — . , .

, , — , . , - , ( ).

? — .

, , . , . . . , , , .

, , , . « » : , , , , , .

, , . , , ( SafeInt (C ++) IntegerLib (C C ++)), , .
, ? , , - « », , .

, , IT . , P ≠ NP , , , , . P NP, , . P = NP, NP- : , RSA DES/AES, .

. — 100 — . , , . , , 1000 , . , .

. , ( , ), . . - , , , , — , . ? , . , , .

, .

最も可能性が高い。

( ) , , . , — , , (Steven G. Krantz, «The Proof is in the Pudding»), , .

:

How Did Software Get So Reliable Without Proof?
An Empirical Study on the Correctness of Formally Verified Distributed Systems
The misfortunes of a trio of mathematicians using Computer Algebra Systems. Can we trust in them?
The mathematical equation that caused the banks to crash
CWE-682: Incorrect Calculation
Experimental Errors and Error Analysis
Misplaced Trust: Kerberos 4 Session Keys
The Patriot Missile Failure
. «: »
. « »
Type I and Type II Errors and Their Application
Cryptographic Right Answers
Mathematical Modelling In Software Reliability