Keras Auto Encoders、パート1：はじめに

内容

• パート1：はじめに
  
• パート2： 多様体学習と潜在変数
  
• パート3： 可変可変エンコーダー（ VAE ）
  
• パート4： 条件付きVAE
  
• パート5： GAN （Generative Adversarial Networks）とテンソルフロー
  
• パート6： VAE + GAN
  

ディープラーニングに飛び込んでいる間、特に新しいオブジェクトを生成するという観点から、自動エンコーダーのトピックに惹かれました。 生成の品質を向上させるために、彼は生成的アプローチのトピックに関するさまざまなブログや文献を読みました。 その結果、蓄積された経験は、 Kerasを構文に導入すると同時に、自分が遭遇したすべての問題領域を簡単に例を挙げて説明する一連の記事に投資することを決めました。

自動エンコーダー

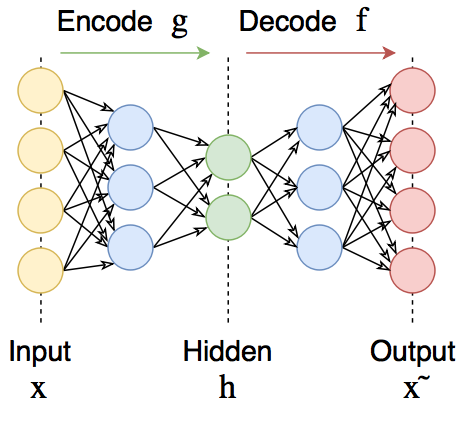
自動エンコーダーは、出力で入力信号を復元する直接分布ニューラルネットワークです。 内部には、モデルを記述するコードである隠しレイヤーがあります 。 自動エンコーダーは 、入力を出力に正確にコピーできないように設計されています。 通常、それらはコードの次元が制限されている（信号の次元よりも小さい）か、 コードでのアクティベーションに対して罰金が科されています 。 入力信号は、コーディング損失によるエラーで復元されますが、それらを最小限に抑えるために、ネットワークは最も重要な機能の選択を学習することを余儀なくされます。



誰も気にしない、キャットへようこそ


自動エンコーダーは2つの部分で構成されます：エンコーダー およびデコーダー 。 エンコーダーは、入力信号をその表現（ code ）に変換します。 、デコーダーはそのコードによって信号を復元します ： 。

変更による自動エンコーダ そして 恒等関数を学習しようとする ある種のエラー機能を最小化する。


この場合、エンコーダー関数ファミリー およびデコーダー エンコーダが最も重要な信号プロパティを選択することを余儀なくされるように、どういうわけか制限されました。

データ自体を圧縮する自動エンコーダーの機能はほとんど使用されません。これは、通常、音声や画像などの特定のデータタイプに対して手動で記述されたアルゴリズムよりも動作が悪いためです。 また、データがネットワークのトレーニングを受けた集団に属していることも重要です。 オートエンコーダーを数字でトレーニングすると、他の何か（たとえば、人間の顔）をエンコードするために使用できません。

ただし、自動エンコーダは、たとえば分類タスクがあり、マークされたペアが少なすぎる場合など、事前トレーニングに使用できます。 または、後で視覚化するためにデータの次元を下げます。 または、入力信号の有用な特性を区別することを学ぶ必要がある場合。

さらに、変分オートエンコーダー（ VAE ）などの開発の一部（後述）、および競合する生成ネットワーク（ GAN ）との組み合わせは、非常に興味深い結果をもたらし、現在は生成モデルの科学の最前線にいます。

ケラス

Kerasは、 theanoまたはtensorflowの上で実行される非常に便利な高レベルの深層学習ライブラリです。 これはレイヤーに基づいており、レイヤーを相互に組み合わせてモデルを取得します。 作成されたモデルとレイヤーは内部パラメーターを保持するため、たとえば、あるモデルでレイヤーをトレーニングし、別のモデルで使用することができます。これは非常に便利です。

Kerasモデルは保存/読み込みが簡単で、シンプルだが深くカスタマイズ可能な学習プロセスがあります。 モデルは、テンソルフロー/テアノコード （テンソル操作など）に自由に埋め込まれます。

データとして、手書き数字データセットMNISTを使用します

ダウンロードしてください：

from keras.datasets import mnist import numpy as np (x_train, y_train), (x_test, y_test) = mnist.load_data() x_train = x_train.astype('float32') / 255. x_test = x_test .astype('float32') / 255. x_train = np.reshape(x_train, (len(x_train), 28, 28, 1)) x_test = np.reshape(x_test, (len(x_test), 28, 28, 1)) 

圧縮自動エンコーダー

まず、完全に接続された2つのレイヤー（エンコーダーとデコーダー）からの低次元コードを使用して、最も単純な（圧縮性の不完全な）自動エンコーダーを作成します。

色の強度は1に正規化されているため、出力層の活性化をS字型と見なします。

エンコーダー、デコーダー、およびオートエンコーダー全体に対して個別のモデルを作成します。 これを行うには、レイヤーのインスタンスを作成し、それらを1つずつ適用し、最後にモデル内のすべてを組み合わせます。

 from keras.layers import Input, Dense, Flatten, Reshape from keras.models import Model def create_dense_ae(): #    encoding_dim = 49 #  #   input_img = Input(shape=(28, 28, 1)) # 28, 28, 1 -  , ,   ,  - #    flat_img = Flatten()(input_img) #     encoded = Dense(encoding_dim, activation='relu')(flat_img) #  #      input_encoded = Input(shape=(encoding_dim,)) flat_decoded = Dense(28*28, activation='sigmoid')(input_encoded) decoded = Reshape((28, 28, 1))(flat_decoded) # ,       ,     #          encoder = Model(input_img, encoded, name="encoder") decoder = Model(input_encoded, decoded, name="decoder") autoencoder = Model(input_img, decoder(encoder(input_img)), name="autoencoder") return encoder, decoder, autoencoder 

モデルを作成してコンパイルしましょう（この場合、コンパイルはエラーの逆伝播の計算のグラフの構築として理解されます ）

 encoder, decoder, autoencoder = create_dense_ae() autoencoder.compile(optimizer='adam', loss='binary_crossentropy') 

パラメーターの数を見てみましょう

 autoencoder.summary() 

 _________________________________________________________________ Layer (type) Output Shape Param # ================================================================= input_1 (InputLayer) (None, 28, 28, 1) 0 _________________________________________________________________ encoder (Model) (None, 49) 38465 _________________________________________________________________ decoder (Model) (None, 28, 28, 1) 39200 ================================================================= Total params: 77,665.0 Trainable params: 77,665.0 Non-trainable params: 0.0 _________________________________________________________________ 

自動エンコーダーをトレーニングします

 autoencoder.fit(x_train, x_train, epochs=50, batch_size=256, shuffle=True, validation_data=(x_test, x_test)) 

 Epoch 46/50 60000/60000 [==============================] - 3s - loss: 0.0785 - val_loss: 0.0777 Epoch 47/50 60000/60000 [==============================] - 2s - loss: 0.0784 - val_loss: 0.0777 Epoch 48/50 60000/60000 [==============================] - 3s - loss: 0.0784 - val_loss: 0.0777 Epoch 49/50 60000/60000 [==============================] - 2s - loss: 0.0784 - val_loss: 0.0777 Epoch 50/50 60000/60000 [==============================] - 3s - loss: 0.0784 - val_loss: 0.0777 

数字機能

 %matplotlib inline import seaborn as sns import matplotlib.pyplot as plt def plot_digits(*args): args = [x.squeeze() for x in args] n = min([x.shape[0] for x in args]) plt.figure(figsize=(2*n, 2*len(args))) for j in range(n): for i in range(len(args)): ax = plt.subplot(len(args), n, i*n + j + 1) plt.imshow(args[i][j]) plt.gray() ax.get_xaxis().set_visible(False) ax.get_yaxis().set_visible(False) plt.show() 

いくつかの画像をエンコードし、興味を引くためにサンプルコードを見てみましょう。

 n = 10 imgs = x_test[:n] encoded_imgs = encoder.predict(imgs, batch_size=n) encoded_imgs[0] 

 array([ 6.64665604, 7.53528595, 3.81508064, 4.66803837, 1.50886345, 5.41063929, 9.28293324, 10.79530716, 0.39599913, 4.20529413, 6.53982353, 5.64758158, 5.25313473, 1.37336707, 9.37590599, 6.00672245, 4.39552879, 5.39900637, 4.11449528, 7.490417 , 10.89267063, 7.74325705, 13.35806847, 3.59005809, 9.75185394, 2.87570286, 3.64097357, 7.86691713, 5.93383646, 5.52847338, 3.45317888, 1.88125253, 7.471385 , 7.29820824, 10.02830505, 10.5430584 , 3.2561543 , 8.24713707, 2.2687614 , 6.60069561, 7.58116722, 4.48140812, 6.13670635, 2.9162209 , 8.05503941, 10.78182602, 4.26916027, 5.17175484, 6.18108797], dtype=float32) 

これらのコードをデコードして、オリジナルと比較します

 decoded_imgs = decoder.predict(encoded_imgs, batch_size=n) plot_digits(imgs, decoded_imgs) 

ディープオートエンコーダー

同じ自動エンコーダーを作成することを気にせずに、多数のレイヤーを使用します。 この場合、彼はより複雑な非線形法則を分離することができます

 def create_deep_dense_ae(): #    encoding_dim = 49 #  input_img = Input(shape=(28, 28, 1)) flat_img = Flatten()(input_img) x = Dense(encoding_dim*3, activation='relu')(flat_img) x = Dense(encoding_dim*2, activation='relu')(x) encoded = Dense(encoding_dim, activation='linear')(x) #  input_encoded = Input(shape=(encoding_dim,)) x = Dense(encoding_dim*2, activation='relu')(input_encoded) x = Dense(encoding_dim*3, activation='relu')(x) flat_decoded = Dense(28*28, activation='sigmoid')(x) decoded = Reshape((28, 28, 1))(flat_decoded) #  encoder = Model(input_img, encoded, name="encoder") decoder = Model(input_encoded, decoded, name="decoder") autoencoder = Model(input_img, decoder(encoder(input_img)), name="autoencoder") return encoder, decoder, autoencoder d_encoder, d_decoder, d_autoencoder = create_deep_dense_ae() d_autoencoder.compile(optimizer='adam', loss='binary_crossentropy') 

モデルの概要を見てみましょう

 d_autoencoder.summary() 

 _________________________________________________________________ Layer (type) Output Shape Param # ================================================================= input_3 (InputLayer) (None, 28, 28, 1) 0 _________________________________________________________________ encoder (Model) (None, 49) 134750 _________________________________________________________________ decoder (Model) (None, 28, 28, 1) 135485 ================================================================= Total params: 270,235.0 Trainable params: 270,235.0 Non-trainable params: 0.0 

パラメーターの数が3倍以上増えました。新しいモデルの方がうまく対処できるかどうか見てみましょう。

 d_autoencoder.fit(x_train, x_train, epochs=100, batch_size=256, shuffle=True, validation_data=(x_test, x_test)) 

 Epoch 96/100 60000/60000 [==============================] - 3s - loss: 0.0722 - val_loss: 0.0724 Epoch 97/100 60000/60000 [==============================] - 3s - loss: 0.0722 - val_loss: 0.0719 Epoch 98/100 60000/60000 [==============================] - 3s - loss: 0.0721 - val_loss: 0.0722 Epoch 99/100 60000/60000 [==============================] - 3s - loss: 0.0721 - val_loss: 0.0720 Epoch 100/100 60000/60000 [==============================] - 3s - loss: 0.0721 - val_loss: 0.0720 

 n = 10 imgs = x_test[:n] encoded_imgs = d_encoder.predict(imgs, batch_size=n) encoded_imgs[0] decoded_imgs = d_decoder.predict(encoded_imgs, batch_size=n) plot_digits(imgs, decoded_imgs) 

損失は​​はるかに小さい値で飽和し、数値はもう少し快適であることがわかります

畳み込み自動エンコーダー

写真を扱うため、データには空間的な不変性が必要です。 使用してみましょう。 畳み込みオートエンコーダーを構築します

 from keras.layers import Conv2D, MaxPooling2D, UpSampling2D def create_deep_conv_ae(): input_img = Input(shape=(28, 28, 1)) x = Conv2D(128, (7, 7), activation='relu', padding='same')(input_img) x = MaxPooling2D((2, 2), padding='same')(x) x = Conv2D(32, (2, 2), activation='relu', padding='same')(x) x = MaxPooling2D((2, 2), padding='same')(x) encoded = Conv2D(1, (7, 7), activation='relu', padding='same')(x) #     (7, 7, 1) .. 49- input_encoded = Input(shape=(7, 7, 1)) x = Conv2D(32, (7, 7), activation='relu', padding='same')(input_encoded) x = UpSampling2D((2, 2))(x) x = Conv2D(128, (2, 2), activation='relu', padding='same')(x) x = UpSampling2D((2, 2))(x) decoded = Conv2D(1, (7, 7), activation='sigmoid', padding='same')(x) #  encoder = Model(input_img, encoded, name="encoder") decoder = Model(input_encoded, decoded, name="decoder") autoencoder = Model(input_img, decoder(encoder(input_img)), name="autoencoder") return encoder, decoder, autoencoder c_encoder, c_decoder, c_autoencoder = create_deep_conv_ae() c_autoencoder.compile(optimizer='adam', loss='binary_crossentropy') c_autoencoder.summary() 

 _________________________________________________________________ Layer (type) Output Shape Param # ================================================================= input_5 (InputLayer) (None, 28, 28, 1) 0 _________________________________________________________________ encoder (Model) (None, 7, 7, 1) 24385 _________________________________________________________________ decoder (Model) (None, 28, 28, 1) 24385 ================================================================= Total params: 48,770.0 Trainable params: 48,770.0 Non-trainable params: 0.0 

 c_autoencoder.fit(x_train, x_train, epochs=64, batch_size=256, shuffle=True, validation_data=(x_test, x_test)) 

 Epoch 60/64 60000/60000 [==============================] - 24s - loss: 0.0698 - val_loss: 0.0695 Epoch 61/64 60000/60000 [==============================] - 24s - loss: 0.0699 - val_loss: 0.0705 Epoch 62/64 60000/60000 [==============================] - 24s - loss: 0.0699 - val_loss: 0.0694 Epoch 63/64 60000/60000 [==============================] - 24s - loss: 0.0698 - val_loss: 0.0691 Epoch 64/64 60000/60000 [==============================] - 24s - loss: 0.0697 - val_loss: 0.0693 

 n = 10 imgs = x_test[:n] encoded_imgs = c_encoder.predict(imgs, batch_size=n) decoded_imgs = c_decoder.predict(encoded_imgs, batch_size=n) plot_digits(imgs, decoded_imgs) 

このネットワークのパラメーターの数は完全に接続されたネットワークのパラメーターの数よりはるかに少ないという事実にもかかわらず、エラー関数ははるかに小さな値で飽和します。

ノイズ除去オートエンコーダー

自動エンコーダーは、データからノイズを除去するようにトレーニングできます。このため、ノイズの多いデータを入力に適用し、出力でノイズのないデータと比較する必要があります。


どこで -ノイズの多いデータ。

Kerasでは 、Lambdaレイヤーの基になるフレームワークから任意の操作をラップできます。 バックエンドモジュールを介して、 tensorflowまたはtheanoから操作にアクセスできます。

入力画像にノイズを発生させ、既に作成された自動エンコーダーの再トレーニングによるノイズを節約するモデルを作成します。

 import keras.backend as K from keras.layers import Lambda batch_size = 16 def create_denoising_model(autoencoder): def add_noise(x): noise_factor = 0.5 x = x + K.random_normal(x.get_shape(), 0.5, noise_factor) x = K.clip(x, 0., 1.) return x input_img = Input(batch_shape=(batch_size, 28, 28, 1)) noised_img = Lambda(add_noise)(input_img) noiser = Model(input_img, noised_img, name="noiser") denoiser_model = Model(input_img, autoencoder(noiser(input_img)), name="denoiser") return noiser, denoiser_model noiser, denoiser_model = create_denoising_model(autoencoder) denoiser_model.compile(optimizer='adam', loss='binary_crossentropy') 

 denoiser_model.fit(x_train, x_train, epochs=200, batch_size=batch_size, shuffle=True, validation_data=(x_test, x_test)) 

 n = 10 imgs = x_test[:batch_size] noised_imgs = noiser.predict(imgs, batch_size=batch_size) encoded_imgs = encoder.predict(noised_imgs[:n], batch_size=n) decoded_imgs = decoder.predict(encoded_imgs[:n], batch_size=n) plot_digits(imgs[:n], noised_imgs, decoded_imgs) 

ノイズの多い画像の数値は見にくいですが、 ノイズを除去するオートエンコーダーはノイズを非常によく除去し、数値は読み取り可能です。

スパース自動エンコーダー

スパース自動エンコーダは単なる自動エンコーダであり、 コード内の値に対するペナルティが損失関数に追加されます。つまり、自動エンコーダはそのようなエラー関数を最小化しようとします。


どこで -コード

-レギュラーレギュライザー（例：L1）：


まばらな自動エンコーダーは、必ずしも中心に向かって先細になるとは限りません。 そのコードは、入力信号よりも大きな次元を持つ場合があります。 アイデンティティ関数をより近づけることを学ぶ 、彼は信号の有用な特性を強調するためにコードで学びます。 正則化のため、中心に向かって拡張するスパースオートエンコーダーでさえ、アイデンティティ関数を直接学習することはできません。

 from keras.regularizers import L1L2 def create_sparse_ae(): encoding_dim = 16 lambda_l1 = 0.00001 #  input_img = Input(shape=(28, 28, 1)) flat_img = Flatten()(input_img) x = Dense(encoding_dim*3, activation='relu')(flat_img) x = Dense(encoding_dim*2, activation='relu')(x) encoded = Dense(encoding_dim, activation='linear', activity_regularizer=L1L2(lambda_l1))(x) #  input_encoded = Input(shape=(encoding_dim,)) x = Dense(encoding_dim*2, activation='relu')(input_encoded) x = Dense(encoding_dim*3, activation='relu')(x) flat_decoded = Dense(28*28, activation='sigmoid')(x) decoded = Reshape((28, 28, 1))(flat_decoded) #  encoder = Model(input_img, encoded, name="encoder") decoder = Model(input_encoded, decoded, name="decoder") autoencoder = Model(input_img, decoder(encoder(input_img)), name="autoencoder") return encoder, decoder, autoencoder s_encoder, s_decoder, s_autoencoder = create_sparse_ae() s_autoencoder.compile(optimizer='adam', loss='binary_crossentropy') 

 s_autoencoder.fit(x_train, x_train, epochs=400, batch_size=256, shuffle=True, validation_data=(x_test, x_test)) 

コードを見てください

 n = 10 imgs = x_test[:n] encoded_imgs = s_encoder.predict(imgs, batch_size=n) encoded_imgs[1] 

 array([ 7.13531828, -0.61532277, -5.95510817, 12.0058918 , -1.29253936, -8.56000137, -7.48944521, -0.05415952, -2.81205249, -8.4289856 , -0.67815018, -11.19531345, -3.4353714 , 3.18580866, -0.21041733, 4.13229799], dtype=float32) 

 decoded_imgs = s_decoder.predict(encoded_imgs, batch_size=n) plot_digits(imgs, decoded_imgs) 

コードの寸法を何らかの方法で解釈できるかどうかを見てみましょう。
すべてのコードの平均を取り、次に、平均化されたコードの各ディメンションが最大値に置き換えられます。

 imgs = x_test encoded_imgs = s_encoder.predict(imgs, batch_size=16) codes = np.vstack([encoded_imgs.mean(axis=0)]*10) np.fill_diagonal(codes, encoded_imgs.max(axis=0)) decoded_features = s_decoder.predict(codes, batch_size=16) plot_digits(decoded_features) 

いくつかの機能が表示されますが、ここでは賢明なものは表示されません。

コード内の値だけでは明らかな意味はありません。デコーダーのレイヤーで発生する値間のトリッキーな相互作用によってのみ、コードから入力信号を復元できます。

コードからオブジェクトを自由に生成することは可能ですか？

この質問に答えるには、コードが何であり、どのように解釈できるかを研究する方が良いでしょう。 それについては次のパートで 。

役立つリンクと文献

この投稿は、 Kerasの作成者Francois CholletによるKeras自動エンコーダに関する投稿の最初の部分の独自の解釈に基づいています。

ディープラーニングブックの 自動エンコーダーに関する章もあります。