内容

パート1：はじめに
パート2： 多様体学習と潜在変数
パート3：可変可変エンコーダー（ VAE ）
パート4： 条件付きVAE
パート5： GAN （Generative Adversarial Networks）とテンソルフロー
パート6： VAE + GAN

最後の部分では、隠し変数とは何かについて説明し、その分布を調べました。また、通常の自動エンコーダーでは隠し変数の分布から新しいオブジェクトを生成することは困難であることに気付きました。新しいオブジェクトを生成するには、 潜在変数のスペースが予測可能でなければなりません。

変分オートエンコーダーは、特定の隠された空間にオブジェクトを表示し、それに応じてそこからサンプリングすることを学習するオートエンコーダーです。したがって、 変分オートエンコーダーも生成モデルのファミリーに属します。

[2]からの図

いずれか1つのディストリビューションを持つ

、あなたは任意の他のものを得ることができます X = g（Z）

たとえばみましょう

-正規正規分布、 $g（Z）= \ frac {Z} {| Z |} + \ frac {Z} {10}$ -ランダム分布も、見た目は完全に異なります

コード

import numpy as np import matplotlib.pyplot as plt %matplotlib inline import seaborn as sns Z = np.random.randn(150, 2) X = Z/(np.sqrt(np.sum(Z*Z, axis=1))[:, None]) + Z/10 fig, axs = plt.subplots(1, 2, sharex=False, figsize=(16,8)) ax = axs[0] ax.scatter(Z[:,0], Z[:,1]) ax.grid(True) ax.set_xlim(-5, 5) ax.set_ylim(-5, 5) ax = axs[1] ax.scatter(X[:,0], X[:,1]) ax.grid(True) ax.set_xlim(-2, 2) ax.set_ylim(-2, 2)

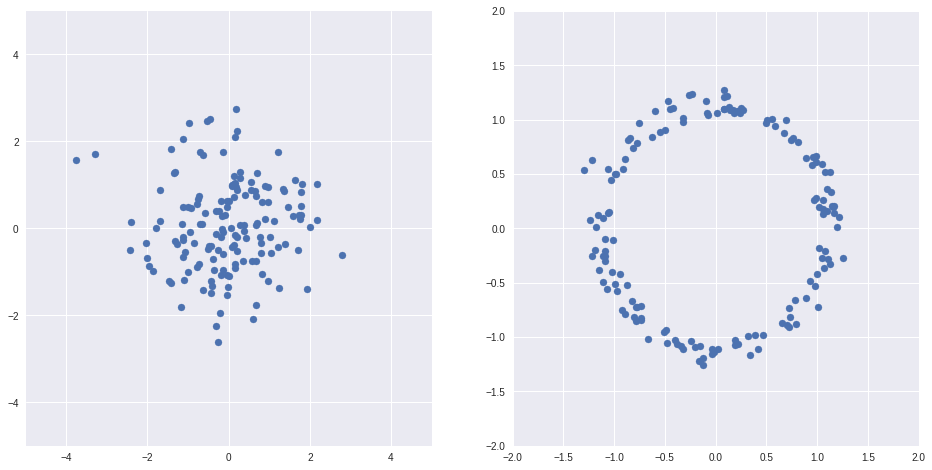
上記の例[1]

したがって、正しい関数を選択すると、通常のオートエンコーダーの隠し変数のスペースを、たとえば分布が正規の場所など、適切なスペースにマッピングできます。そして戻って。

一方、隠されたスペースを別のスペースに表示することを特に学ぶ必要はありません。有用な隠しスペースがある場合、正しい自動エンコーダーはそれらを途中で学習しますが、最終的に必要なスペースに表示します。

以下はVAEの基礎となる複雑ですが必要な理論です。私は、 [1、Variation Autoencodersのチュートリアル、Carl Doersch、2016]から最も重要なものを絞り出そうとしました。

させる

隠された変数であり、

-データ。例として描かれた数字を使用して、サンプルを生成した自然な生成プロセスを考えます。

$P（X）= \ int_ {z} P（X | Z）P（Z）dZ$

写真内の数字の画像の確率的分布、すなわち原則として図の特定の画像が描かれる確率（絵が図のように見えない場合、この確率は非常に小さく、逆も同様です）
-隠れた要因の確率分布、たとえば、ストロークの太さの分布、
-与えられた隠された要因の画像の確率分布、同じ要因は異なる画像につながる可能性があります（同じ条件で同じ人が正確に同じ数字を描くわけではありません）。

想像してみて

いくつかの生成関数の合計として

そしていくつかの複雑なノイズ $\イプシロン$

$P（X | Z）= f（Z）+ \イプシロン$

私たちは、いくつかのメトリックがトレーニングに近いオブジェクトを作成する人工的な生成プロセスを構築したい

。

$P（X; \シータ）= \ int_ {z} P（X | Z; \シータ）P（Z）dZ \ \ \（1）$

そしてまた

$P（X | Z; \シータ）= f（Z; \シータ）+ \イプシロン$

$f（Z; \シータ）$ -モデルが表す関数のファミリー、および $\シータ$ -そのパラメーター。メトリックを選択して、どのようなノイズが私たちに見えるかを選択します $\イプシロン$ 。メトリック L_2

、その後、通常のノイズを考慮してから：

$P（X | Z; \シータ）= N（X | f（Z; \シータ）、\シグマ^ 2 I）、$

最尤法の原理に基づいて、最適化することは私たちに残っています $\シータ$ 最大化するために P（X）

、つまりサンプルからのオブジェクトの出現の確率。

問題は、積分を直接最適化できないことです（1）。空間は高次元である可能性があり、多くのオブジェクトがあり、メトリックは悪いです。一方、考えてみると、それぞれの特定の

非常に小さなサブセットのみが結果として得られます

残りのために

ゼロに非常に近くなります。
最適化するときは、良いものからのみサンプリングするだけで十分です。

。

知るために

サンプリングし、新しいディストリビューションを導入する必要があります Q（Z | X）

どの依存

分布を表示します $Z \ sim Q$ それはこれにつながる可能性があります

。

最初に、Kullback – Leibler距離（2つの分布の「類似性」の非対称尺度、詳細[3] ）を記述します。

そして本物の

：

$KL [Q（Z | X）|| P（Z | X）] = \ mathbb {E} _ {Z \ sim Q} [\ log Q（Z | X）-\ log P（Z | X）]$

ベイズ公式を適用します。

$KL [Q（Z | X）|| P（Z | X）] = \ mathbb {E} _ {Z \ sim Q} [\ log Q（Z | X）-\ log P（X | Z）-\ log P（Z）] + \ log P（X）$

カルバック・ライブラー距離をもう1つ選びます。

$KL [Q（Z | X）|| P（Z | X）] = KL [Q（Z | X）|| \ log P（Z）]-\ mathbb {E} _ {Z \ sim Q} [\ log P（X | Z）] + \ log P（X）$

その結果、IDを取得します。

$\ log P（X）-KL [Q（Z | X）|| P（Z | X）] = \ mathbb {E} _ {Z \ sim Q} [\ log P（X | Z）]-KL [ Q（Z | X）|| P（Z）]$

このアイデンティティは、 バリエーション自動エンコーダーの基礎であり、 Q（Z | X）

そして

。

させる

そして

パラメーターに依存します。 $Q（Z | X; \ theta_1）$ そして $P（X | Z; \ theta_2）$ 、そして P（Z）

-通常

次に取得します：

$\ log P（X; \ theta_2）-KL [Q（Z | X; \ theta_1）|| P（Z | X; \ theta_2）] = \ mathbb {E} _ {Z \ sim Q} [\ log P （X | Z; \ theta_2）]-KL [Q（Z | X; \ theta_1）|| N（0、I）]$

取得したものを詳しく見てみましょう。

第一に $Q（Z | X; \ theta_1）$ 、 $P（X | Z; \ theta_2）$ 疑い深くエンコーダーとデコーダーに似ています（より正確には、デコーダーは式で $P（X | Z; \ theta_2）= f（Z; \ theta_2）+ \イプシロン$ ）、
アイデンティティの左側-トレーニングサンプルの要素に対して最大化する値 +何らかのエラー $KL \（KL（x、y）\ ge 0 \ \ \ forall x、y）$ うまくいけば、十分な容量を持つ 0になる
右側は勾配降下法で最適化できる値です。最初の項は予測の質の意味を持ちます値デコーダ 2番目の項は、分布間の距離KL $Z \ sim Q$ エンコーダーが特定のものについて予測するもの、および配布すべてのためにすぐに。

勾配降下で右側を最適化できるようにするために、次の2つのことに対処します。

1.より正確には、 $Q（Z | X; \ theta_1）$

通常

正規分布により選択：

$Q（Z | X; \ theta_1）= N（\ mu（X; \ theta_1）、\ Sigma（X; \ theta_1））$

つまり、それぞれのエンコーダ

2つの値を予測：平均 $\ mu$ とバリエーション $\シグマ$ 値が既にサンプリングされている正規分布。すべてこのように機能します：

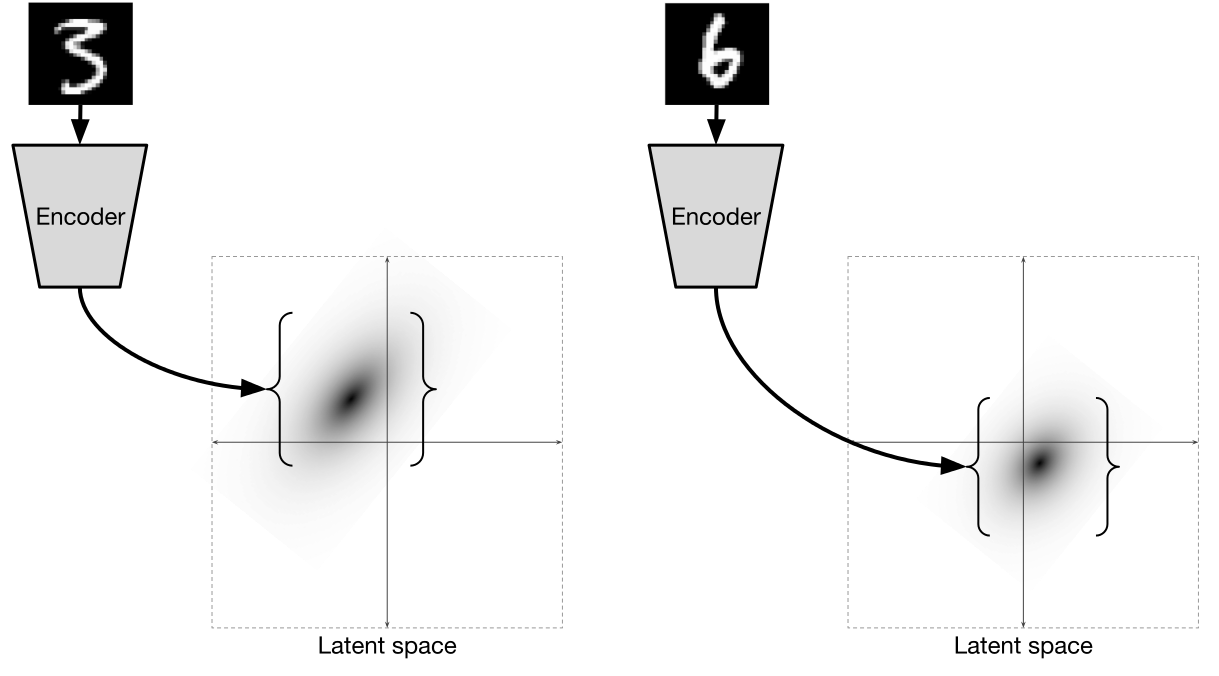[2]からの図

個々のデータポイントごと

エンコーダは正規分布を予測します

$P（Z | X）= N（\ mu（X）、\シグマ（X））$

限界分布の場合

：

それは式に由来し、それは驚くべきことです。

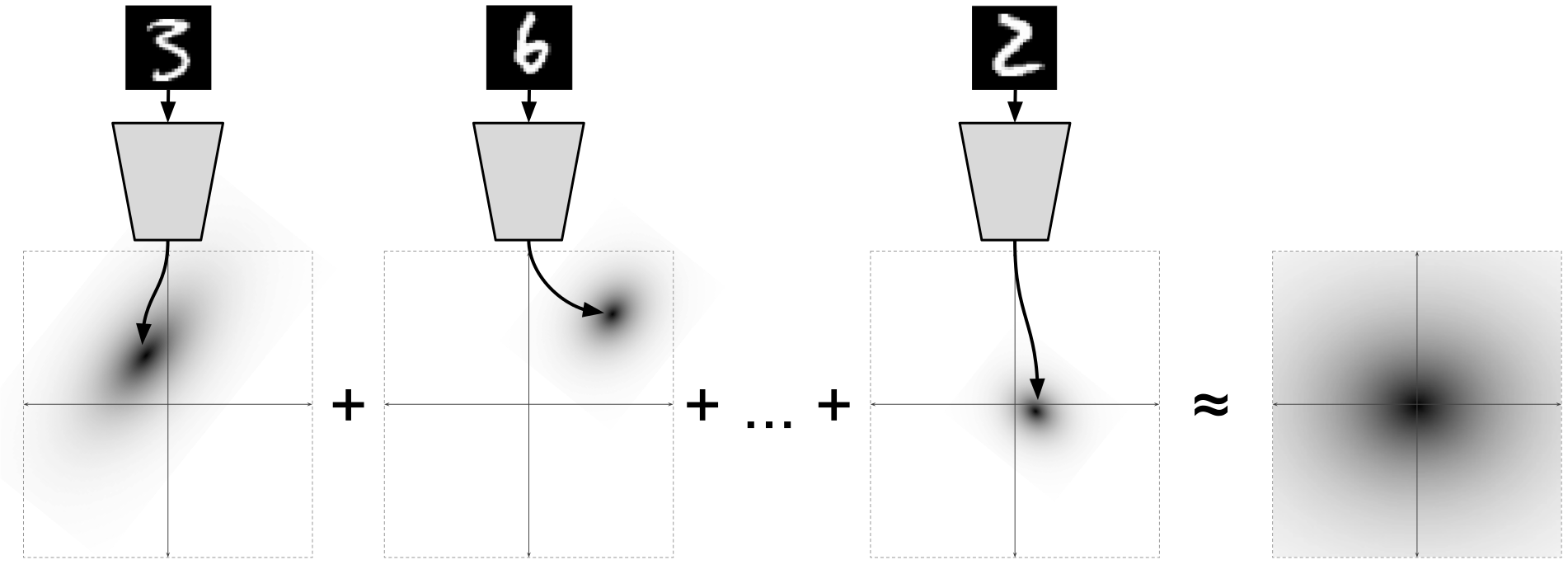[2]からの図

同時に $KL [Q（Z | X; \ theta_1）|| N（0、I）]$ 次の形式を取ります。

$KL [Q（Z | X; \ theta_1）|| N（0、I）] = \ frac {1} {2} \左（tr（\シグマ（X））+ \ mu（X）^ T \ mu （X）-k-\ log \ det \ Sigma（X）\右）$

2.エラーを拡散する方法を見つけます $\ mathbb {E} _ {Z \ sim Q} [\ log P（X | Z; \ theta_2）]$

事実は、ここでランダムな値をとることです $Z \ sim Q（Z | X; \ theta_1）$ デコーダーに送信します。
ランダムな値を介してエラーを直接伝播することは不可能であることは明らかであるため、いわゆる再パラメーター化の トリックが使用されます。

スキームは次のとおりです。

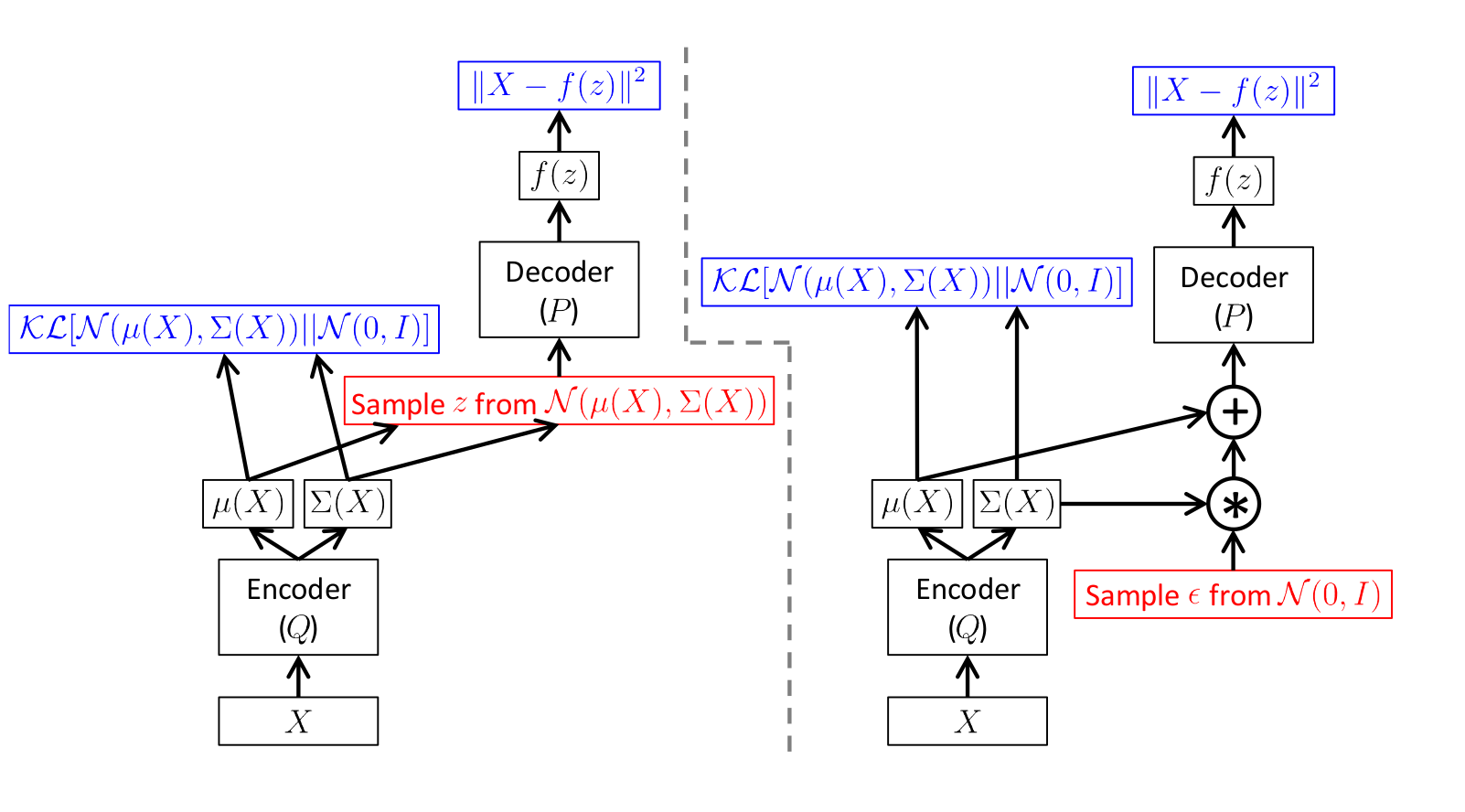[1]からの図

左の写真はトリックのないスキームで、右の写真はトリックのあるスキームです。
サンプリングは赤で、エラー計算は青で表示されます。
つまり、実際には、エンコーダーによって予測された標準偏差を取得するだけです $\シグマ$ から乱数を掛ける N（0、I）

予測平均を追加します $\ mu$ 。
両方のスキームでの直接伝播はまったく同じですが、エラーの逆分布は正しいスキームで機能します。

このような変分オートエンコーダーをトレーニングした後、デコーダーは本格的な生成モデルになります。実際、主にデコーダを生成モデルとして個別にトレーニングするために、エンコーダも必要です。

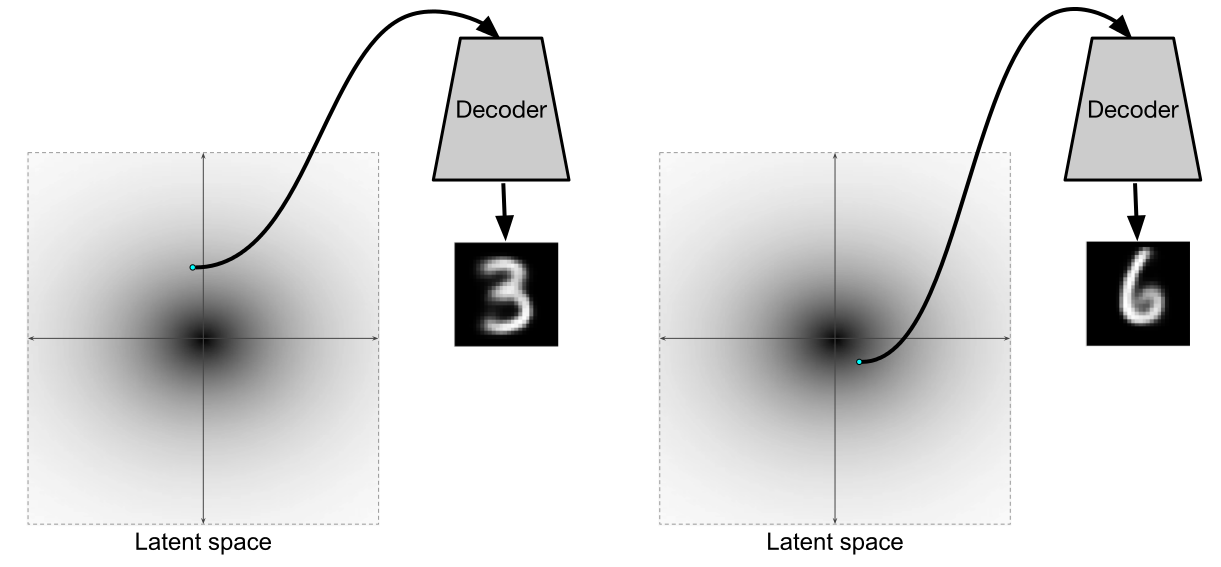[2]からの図

[1]からの図

しかし、エンコーダーとデコーダーがフルオートエンコーダーを形成する代わりに使用できるという事実は、非常に優れています。

ケラスのVAE

バリエーションオートエンコーダーとは何かを理解したので、 Kerasで作成します。

必要なライブラリとデータセットをインポートします。

 import sys import numpy as np import matplotlib.pyplot as plt %matplotlib inline import seaborn as sns from keras.datasets import mnist (x_train, y_train), (x_test, y_test) = mnist.load_data() x_train = x_train.astype('float32') / 255. x_test = x_test .astype('float32') / 255. x_train = np.reshape(x_train, (len(x_train), 28, 28, 1)) x_test = np.reshape(x_test, (len(x_test), 28, 28, 1))

主なパラメータを設定します。ディメンション2の隠されたスペースを使用して、後でそこから生成し、結果を視覚化します。
注：Dimension 2は非常に小さいため、数値が非常にぼやけていると予想する必要があります。

 batch_size = 500 latent_dim = 2 dropout_rate = 0.3 start_lr = 0.0001

変分オートエンコーダーのモデルを書きましょう。

トレーニングをより速く、より良く行うために、 ドロップアウトとバッチ正規化レイヤーを追加します。

デコーダーでは、アクティベーションとして漏れやすいReLUを使用します。これは、アクティベーションなしの密なレイヤーの後に別のレイヤーとして追加します。
サンプリング関数はサンプリング値を実装します

から

再パラメータ化トリックを使用します。

vae_lossは方程式の右側です：

$\ log P（X; \ theta_2）-KL [Q（Z | X; \ theta_1）|| P（Z | X; \ theta_2）] = \ mathbb {E} _ {Z \ sim Q} [\ log P （X | Z; \ theta_2）]-\左（\ frac {1} {2} \左（tr（\シグマ（X））+ \ mu（X）^ T \ mu（X）-k-\ log \ det \シグマ（X）\右）\右）$

損失としてさらに使用されます。

 from keras.layers import Input, Dense from keras.layers import BatchNormalization, Dropout, Flatten, Reshape, Lambda from keras.models import Model from keras.objectives import binary_crossentropy from keras.layers.advanced_activations import LeakyReLU from keras import backend as K def create_vae(): models = {} #  Dropout  BatchNormalization def apply_bn_and_dropout(x): return Dropout(dropout_rate)(BatchNormalization()(x)) #  input_img = Input(batch_shape=(batch_size, 28, 28, 1)) x = Flatten()(input_img) x = Dense(256, activation='relu')(x) x = apply_bn_and_dropout(x) x = Dense(128, activation='relu')(x) x = apply_bn_and_dropout(x) #    #  ,    ,    z_mean = Dense(latent_dim)(x) z_log_var = Dense(latent_dim)(x) #   Q    def sampling(args): z_mean, z_log_var = args epsilon = K.random_normal(shape=(batch_size, latent_dim), mean=0., stddev=1.0) return z_mean + K.exp(z_log_var / 2) * epsilon l = Lambda(sampling, output_shape=(latent_dim,))([z_mean, z_log_var]) models["encoder"] = Model(input_img, l, 'Encoder') models["z_meaner"] = Model(input_img, z_mean, 'Enc_z_mean') models["z_lvarer"] = Model(input_img, z_log_var, 'Enc_z_log_var') #  z = Input(shape=(latent_dim, )) x = Dense(128)(z) x = LeakyReLU()(x) x = apply_bn_and_dropout(x) x = Dense(256)(x) x = LeakyReLU()(x) x = apply_bn_and_dropout(x) x = Dense(28*28, activation='sigmoid')(x) decoded = Reshape((28, 28, 1))(x) models["decoder"] = Model(z, decoded, name='Decoder') models["vae"] = Model(input_img, models["decoder"](models["encoder"](input_img)), name="VAE") def vae_loss(x, decoded): x = K.reshape(x, shape=(batch_size, 28*28)) decoded = K.reshape(decoded, shape=(batch_size, 28*28)) xent_loss = 28*28*binary_crossentropy(x, decoded) kl_loss = -0.5 * K.sum(1 + z_log_var - K.square(z_mean) - K.exp(z_log_var), axis=-1) return (xent_loss + kl_loss)/2/28/28 return models, vae_loss models, vae_loss = create_vae() vae = models["vae"]

注：からサンプリングする関数を持つLambdaレイヤーを使用しました N（0、I）

基礎となるフレームワークから。これには明らかにバッチサイズが必要です。このレイヤーが存在するすべてのモデルで、バッチのサイズだけを送信するように強制されます（つまり、 エンコーダーとvaeで ）。

最適化関数はAdamまたはRMSpropを使用し 、両方とも良好な結果を示します。

 from keras.optimizers import Adam, RMSprop vae.compile(optimizer=Adam(start_lr), loss=vae_loss)

さまざまな数字と数字の行を描画するためのコード

コード

 digit_size = 28 def plot_digits(*args, invert_colors=False): args = [x.squeeze() for x in args] n = min([x.shape[0] for x in args]) figure = np.zeros((digit_size * len(args), digit_size * n)) for i in range(n): for j in range(len(args)): figure[j * digit_size: (j + 1) * digit_size, i * digit_size: (i + 1) * digit_size] = args[j][i].squeeze() if invert_colors: figure = 1-figure plt.figure(figsize=(2*n, 2*len(args))) plt.imshow(figure, cmap='Greys_r') plt.grid(False) ax = plt.gca() ax.get_xaxis().set_visible(False) ax.get_yaxis().set_visible(False) plt.show() n = 15 #   15x15  digit_size = 28 from scipy.stats import norm #     N(0, I),   ,          grid_x = norm.ppf(np.linspace(0.05, 0.95, n)) grid_y = norm.ppf(np.linspace(0.05, 0.95, n)) def draw_manifold(generator, show=True): #     figure = np.zeros((digit_size * n, digit_size * n)) for i, yi in enumerate(grid_x): for j, xi in enumerate(grid_y): z_sample = np.zeros((1, latent_dim)) z_sample[:, :2] = np.array([[xi, yi]]) x_decoded = generator.predict(z_sample) digit = x_decoded[0].squeeze() figure[i * digit_size: (i + 1) * digit_size, j * digit_size: (j + 1) * digit_size] = digit if show: #  plt.figure(figsize=(15, 15)) plt.imshow(figure, cmap='Greys_r') plt.grid(None) ax = plt.gca() ax.get_xaxis().set_visible(False) ax.get_yaxis().set_visible(False) plt.show() return figure

多くの場合、モデルをトレーニングするプロセスでは、 learning_rateの変更、中間結果の保存、モデルの保存、画像の描画など、いくつかのアクションを実行する必要があります。

これを行うために、 kerasには、トレーニングが始まる前にfitメソッドに渡されるコールバックがあります。たとえば、学習プロセスで学習率に影響を与えるために、 LearningRateScheduler 、 ReduceLROnPlateauなどのコールバックがあり、モデルを保存します-ModelCheckpoint 。

TensorBoardで学習プロセスを監視するには、別のコールバックが必要です。それは自動的にログファイルに時代の間で考慮されるすべてのメトリックと損失を追加します。

学習プロセスで任意の機能を実行する必要がある場合のために、 LambdaCallbackがあります。たとえば、時代やバッチの間など、与えられたトレーニングの瞬間に任意の関数の実行を開始します。
学習プロセスに従い、数字がどのように生成されるかを研究します N（0、I）

。

 from IPython.display import clear_output from keras.callbacks import LambdaCallback, ReduceLROnPlateau, TensorBoard # ,     ,    figs = [] latent_distrs = [] epochs = [] # ,     save_epochs = set(list((np.arange(0, 59)**1.701).astype(np.int)) + list(range(10))) #       imgs = x_test[:batch_size] n_compare = 10 #  generator = models["decoder"] encoder_mean = models["z_meaner"] # ,       def on_epoch_end(epoch, logs): if epoch in save_epochs: clear_output() #   output #      decoded = vae.predict(imgs, batch_size=batch_size) plot_digits(imgs[:n_compare], decoded[:n_compare]) #   figure = draw_manifold(generator, show=True) #     z     epochs.append(epoch) figs.append(figure) latent_distrs.append(encoder_mean.predict(x_test, batch_size)) #  pltfig = LambdaCallback(on_epoch_end=on_epoch_end) # lr_red = ReduceLROnPlateau(factor=0.1, patience=25) tb = TensorBoard(log_dir='./logs') #   vae.fit(x_train, x_train, shuffle=True, epochs=1000, batch_size=batch_size, validation_data=(x_test, x_test), callbacks=[pltfig, tb], verbose=1)

これで、 TensorBoardがインストールされている場合、学習プロセスに従うことができます。

このエンコーダーが画像を復元する方法は次のとおりです。

そして、これはからのサンプリング結果です N（0 | I）

数字を生成する学習プロセスは次のとおりです。

GIF

隠された空間でのコードの配布：

GIF

完全に正常ではありませんが、かなり近いです（特に、隠されたスペースの寸法が2だけであることを考慮して）。

TensorBoardの学習曲線

GIF作成コード

 from matplotlib.animation import FuncAnimation from matplotlib import cm import matplotlib def make_2d_figs_gif(figs, epochs, fname, fig): norm = matplotlib.colors.Normalize(vmin=0, vmax=1, clip=False) im = plt.imshow(np.zeros((28,28)), cmap='Greys_r', norm=norm) plt.grid(None) plt.title("Epoch: " + str(epochs[0])) def update(i): im.set_array(figs[i]) im.axes.set_title("Epoch: " + str(epochs[i])) im.axes.get_xaxis().set_visible(False) im.axes.get_yaxis().set_visible(False) return im anim = FuncAnimation(fig, update, frames=range(len(figs)), interval=100) anim.save(fname, dpi=80, writer='imagemagick') def make_2d_scatter_gif(zs, epochs, c, fname, fig): im = plt.scatter(zs[0][:, 0], zs[0][:, 1], c=c, cmap=cm.coolwarm) plt.colorbar() plt.title("Epoch: " + str(epochs[0])) def update(i): fig.clear() im = plt.scatter(zs[i][:, 0], zs[i][:, 1], c=c, cmap=cm.coolwarm) im.axes.set_title("Epoch: " + str(epochs[i])) im.axes.set_xlim(-5, 5) im.axes.set_ylim(-5, 5) return im anim = FuncAnimation(fig, update, frames=range(len(zs)), interval=150) anim.save(fname, dpi=80, writer='imagemagick') make_2d_figs_gif(figs, epochs, "./figs3/manifold.gif", plt.figure(figsize=(10,10))) make_2d_scatter_gif(latent_distrs, epochs, y_test, "./figs3/z_distr.gif", plt.figure(figsize=(10,10)))

このようなタスクの次元2は非常に小さく、数値は非常にぼやけており、良い数値と数値の間には破れた数値も多数あることがわかります。
次のパートでは、目的のラベルの番号を生成する方法、破れたラベルを取り除く方法、およびスタイルをある数字から別の数字に転送する方法について説明します。

役立つリンクと文献

理論的な部分は次の記事に基づいています。
[1] Variation Autoencodersのチュートリアル、Carl Doersch、2016年、 https： //arxiv.org/abs/1606.05908
そして実際にはそれの要約です

Isaac Dykemanブログから多くの写真が撮影されています。
[2] Isaac Dykeman、 http： //ijdykeman.imtqy.com/ml/2016/12/21/cvae.html

ロシア語のカルバック・ライブラー距離の詳細については、こちらをご覧ください。
[3] http://www.machinelearning.ru/wiki/images/d/d0/BMMO11_6.pdf

コードは、 Francois Cholletの記事に部分的に基づいています。
[4] https://blog.keras.io/building-autoencoders-in-keras.html

他の興味深いリンク：
http://blog.fastforwardlabs.com/2016/08/12/introducing-variational-autoencoders-in-prose-and.html
http://kvfrans.com/variational-autoencoders-explained/

Keras Auto Encoders、パート3：Variable Variable Auto Encoders（VAE）

内容

1.より正確には、 $Q（Z | X; \ theta_1）$

2.エラーを拡散する方法を見つけます $\ mathbb {E} _ {Z \ sim Q} [\ log P（X | Z; \ theta_2）]$

ケラスのVAE

役立つリンクと文献

More articles: