Сглаживание изображений фильтром анизотропной диффузии Перона и Малика

— , , «» .

, , Fortran .


— , — .

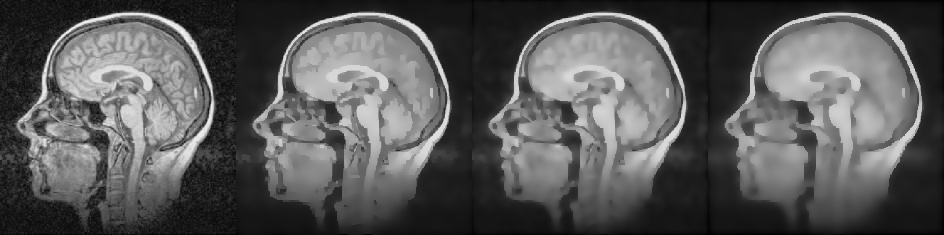画像処理（特にマシンビジョン）では、セグメンテーションまたは領域の境界の強調表示のタスクは珍しくありません。 しかし、カメラ、断層撮影装置などの物理デバイスからの情報を処理した結果として画像が取得される場合、通常はノイズが多く、画像のノイズの性質は異なる場合があります-物理現象とさまざまなアルゴリズムおよびハードウェア機能によって引き起こされます。

ノイズは、セグメンテーションと境界抽出のタスクを非常に複雑にします。したがって、通常、このような画像はまずノイズを平滑化することに加えて、他のすべてを平滑化するいくつかの平滑化フィルターを最初に通過します。 画像を2つの変数の関数と見なすと、画像はより滑らかになり、画像上の領域の選択が非常に容易になります。

ただし、これらのフィルターを使用すると、画像内の領域の境界も滑らかになります。 つまり、スムージングが強いほど、元の境界から離れます。 一部のタスクではこれが許容される場合がありますが、たとえば医学では、人体のさまざまな部分の断層撮影画像の自動セグメンテーションでは、領域の元の境界を保持することが重要です（ここでは、内臓、その変形、さまざまな腫瘍などが領域の役割を果たす）。 。

任意の画像に対するドメイン境界の正式な数学的に厳密な定義はありません（これにより、画像処理の理論における多くの問題が解決されます）。

ペロンとマリクフィルター

1990年にこれらの数学者による記事で最初に説明されました（記事へのリンクは、投稿の最後の「ソース」にあります）。 理論的な詳細については触れませんが、少なくとも表面的にはフィルターがどのように機能するかを検討します。

以下、グレースケール画像が考慮されます。 色については、各チャンネルを個別に滑らかにすることができます。

理論

そのため、異方性拡散フィルターでは、平滑化された画像は、次の数理物理学の方程式を解くことによって得られる一連の画像のメンバーです。

$$

$$I_ {t}（x、y、t）= div（c（x、y、t）\ nabla I（x、y、t））\：\：\：\：\：\：\：\：\：\： （1）$$

初期状態では：

$$

$$I（x、y、0）= I_ {0}（x、y）$$

どこで：

$$$I（x、y、t）$ -画像の1​​パラメータファミリ。 もっと $$$t$ 、元の画像のぼかしの程度が大きくなります。
$$$I_ {0}（x、y）$ -ソース画像;
$$$I_ {t}$ -の誘導体 $$$t$ ;
$$$div$ -分岐演算子。
$$$\ nabla$ -勾配;

理論の観点から、画像は2つの変数の特定の連続関数であり、画像自体（ピクセルのマトリックス）はこの関数の離散化です。 さらに、0はイメージポイントのゼロ輝度に対応します。つまり、黒色を示します。

本質的に、異方性拡散フィルターはガウスフィルターを修正したものです。

まだ考慮されていない関数の代わりに代入すると、 $$$c（x、y、t）$ ユニット、すなわち $$$s（x、y、t）\ equiv 1$ 、等方性拡散の方程式が得られます：

$$

$$I_ {t}（x、y、t）= div（\ nabla I（x、y、t））= \ frac {\ partial ^ {2} I} {\ partial x ^ {2}} + \ frac {\ partial ^ {2} I} {\ partial y ^ {2}}$$

数学者のKoenderinkとGumelは、ぼやけた画像のファミリーがパラメーターによって何であるかを示しました $$$t$ は、ガウスカーネルを使用した画像関数の畳み込み方程式の解として同等に取得できます（これはガウスフィルターです）。

$$

$$I（x、y、t）= I_ {0}（x、y）* G（x、y; t）$$

どこで：

$$$*$ -畳み込み演算子。
$$$G（x、y; t）= {\ frac {1} {2 \ pi t ^ {2}}} e ^ {-{\ frac {x ^ {2} + y ^ {2}} {2t ^ {2}}}}$ 期待値がゼロのガウスカーネルの関数であり、 $$$t$ 標準偏差;

明らかに機能する $$$s（x、y、t）$ 平滑化の「アジャスター」の役割を果たします。

フィルター方程式（ 1 ）に基づいて、イメージポイントの初期値を保持するには、時間微分がゼロに等しい（つまり、ぼかしレイヤーの値が一定である）必要があります。 関数について次の条件を取得します $$$c$ ：

$$$c（x、y、t）= 0$ -国境で;
$$$c（x、y、t）= 1$ -領域内、つまり領域内では、通常のガウスぼかしが発生するはずです。

ペローナとマリクは画像関数勾配を使用しました $$$\ nabla I$ 領域の境界の単純でかなり正確な近似として。 勾配のノルムが大きいほど、境界線はよりシャープになります。 これに基づいて、以下を取得します。

$$

$$c（x、y、t）= g（|| \ nabla I（x、y、t）||）$$

どこで $$$g（。）$ -セグメント上の値の範囲を持ついくつかの関数 $$$[0; 1]$ 。

勾配のノルムを介した境界のファジー定義により、関数 $$$g$ 単調な衰弱でした。

ペローナとマリクは、機能のための2つのオプションを提案しました $$$g$ ：

$$

$$g（x）= e ^ {-（\ frac {x} {k}）^ {2}} \：\：\：\：\：\：\：\：\：（2）$$

$$

$$g（x）= \ frac {1} {1 +（\ frac {x} {k}）^ {2}} \：\：\：\：\：\：\：\：\：（3）$$

どこで $$$k$ -経験的に、またはノイズの「メートル」によって決定されるパラメーター。

2番目の関数をより詳細に検討します（式3）。 これを行うには、関数グラフを作成します $$$g$ いくつかの異なる $$$k$ 。



大きいことがわかる $$$k$ 、関数の値が大きいほど $$$g$ 任意の固定小数点用。

たとえば、画像のある時点で、それを呼び出してみましょう $$$（\チルダ{x}、\チルダ{y}）$ 、我々はレベルで勾配ノルムの値を知っています $$$\チルダ{t}$ ： $$$|| \ nabla I（\チルダ{x}、\チルダ{y}、\チルダ{t}）|| = 4$ 。 それから $$$g_ {k = 2}（|| \ nabla I（\チルダ{x}、\チルダ{y}、\チルダ{t}）||）= g_ {k = 2}（4）= 0.2$ ながら $$$g_ {k = 16}（4）\約0.94$ 。 最初のケースでは、ポイントで値をわずかに「平滑化」しました。これは、以前に導入した基準に従って、ほとんどの場合、境界にあり、2番目では、関数の値 $$$g$ それぞれほぼ1つであるため、ポイントは境界と見なされず、通常のガウスぼかしによって平滑化されます。

このように $$$k$ ノイズの「バリア」として機能し、 $$$k$ 境界と見なされるポイントの「要件」が増加します。

離散化

フィルターアルゴリズムに直接進むために、方程式を離散化します。 数学的計算の観点から十分に単純であり、計算に対する要求の厳しいものは、差分法による方程式の離散化です。 便宜上、主な方程式を次のように書き直します。

$$

$$\ frac {\ partial} {\ partial t} I（x、y、t）= \ frac {\ partial} {\ partial x} \ left [c（x、y、t）\ frac {\ partial} { \部分x} I（x、y、t）\右] + \ frac {\ partial} {\ partial y} \左[c（x、y、t）\ frac {\ partial} {\ partial y} I （x、y、t）\右]$$

次に、有限差分明示的スキームを記述します。

$$$I（x、y、t + \ Delta t）-I（x、y、t）= \\ \ hspace {55mm} = \ frac {\ Delta t} {（\ Delta x）^ {2}} \左[c（x + \ frac {\ Delta x} {2}、y、t）\ cdot（I（x + \ Delta x、y、t）-I（x、y、t））-\\ \ hspace {68mm } -c（x- \ frac {\ Delta x} {2}、y、t）\ cdot（I（x、y、t）-I（x- \ Delta x、y、t））\ right] + \\ \ hspace {55mm} + \ frac {\ Delta t} {（\ Delta y）^ {2}} \ left [c（x、y + \ frac {\ Delta y} {2}、t）\ cdot（ I（x、y + \ Delta y、t）-I（x、y、t））-\\ \ hspace {68mm} -c（x、y- \ frac {\ Delta y} {2}、t）\ cdot（I（x、y、t）-I（x、y- \ Delta y、t））\ right]$

結果の明示的なスキームの安定性条件を書き留めることは、方程式の非線形性のために重要な作業です。 しかし、ペローナとマリクは $$$\ Delta x = \ Delta y = 1$ 回路は誰にとっても安定しています $$$0 \ leq \ Delta t \ leq \ frac {1} {4}$ 。 この事実と、ピクセル値のマトリックスが画像関数の離散表現になるという事実を考えると、メインの計算スキームをマトリックス形式に書き換えます。

$$

$$I_ {i、j} ^ {t + 1} = I_ {i、j} ^ {t} + \ Delta t \ left [{C_ {N}} _ {i、j} ^ {t} \ cdot \ bigtriangledown_ {N} I_ {i、j} ^ {t} + {C_ {S}} _ {i、j} ^ {t} \ cdot \ bigtriangledown_ {S} I_ {i、j} ^ {t} + { C_ {E}} _ {i、j} ^ {t} \ cdot \ bigtriangledown_ {E} I_ {i、j} ^ {t} + {C_ {W}} _ {i、j} ^ {t} \ cdot \ bigtriangledown_ {W} I_ {i、j} ^ {t} \右]$$

どこで：

$$$\ bigtriangledown_ {N} I_ {i、j} ^ {t} = I_ {i-1、j} ^ {t} -I_ {i、j} ^ {t}$
$$$\ bigtriangledown_ {S} I_ {i、j} ^ {t} = I_ {i + 1、j} ^ {t} -I_ {i、j} ^ {t}$
$$$\ bigtriangledown_ {E} I_ {i、j} ^ {t} = I_ {i、j + 1} ^ {t} -I_ {i、j} ^ {t}$
$$$\ bigtriangledown_ {W} I_ {i、j} ^ {t} = I_ {i、j-1} ^ {t} -I_ {i、j} ^ {t}$

$$${C_ {N}} _ {i、j} ^ {t} = g（|| {（\ nabla I）} _ {i-1 / 2、j} ^ {t} ||）$
$$${C_ {S}} _ {i、j} ^ {t} = g（|| {（\ nabla I）} _ {i + 1/2、j} ^ {t} ||）$
$$${C_ {E}} _ {i、j} ^ {t} = g（|| {（\ nabla I）} _ {i、j + 1/2} ^ {t} ||）$
$$${C_ {W}} _ {i、j} ^ {t} = g（|| {（\ nabla I）} _ {i、j-1 / 2} ^ {t} ||）$

係数を計算するには $$$C$ 最初に、勾配の割合を計算する必要があります。 勾配ノルムを近似する最も簡単な方法は、差分グリッドの対応する軸上の勾配投影の長さと置き換えることです。

$$${C_ {N}} _ {i、j} ^ {t} = g（| \ bigtriangledown_ {N} I_ {i、j} ^ {t} |）$
$$${C_ {S}} _ {i、j} ^ {t} = g（| \ bigtriangledown_ {S} I_ {i、j} ^ {t} |）$
$$${C_ {E}} _ {i、j} ^ {t} = g（| \ bigtriangledown_ {E} I_ {i、j} ^ {t} |）$
$$${C_ {W}} _ {i、j} ^ {t} = g（| \ bigtriangledown_ {W} I_ {i、j} ^ {t} |）$

これはわずかに異なる拡散方程式を近似するかなり粗い置換ですが、それでも画像の全体的な明るさを保持し、計算速度において後者を上回る勾配ノルムのより正確な近似と比較してほぼ同一の結果をもたらします。

最終的な計算式は次のようになります。

$$

$$I_ {i、j} ^ {t + 1} = I_ {i、j} ^ {t} + \ Delta t \ left [g（| N |）\ cdot N + g（| S |）\ cdot S + g（| E |）\ cdot E + g（| W |）\ cdot W \ right] \：\：\：\：\：\：\：\：\：（4）$$

どこで：

$$$N = \ bigtriangledown_ {N} I_ {i、j} ^ {t}$
$$$S = \ bigtriangledown_ {S} I_ {i、j} ^ {t}$
$$$E = \ bigtriangledown_ {E} I_ {i、j} ^ {t}$
$$$W = \ bigtriangledown_ {W} I_ {i、j} ^ {t}$

概略的に、設計スキームは下図のように描くことができます。


つまり、新しい値は、現在の値とマトリックスセルの4つの近傍の値に依存します。 問題が発生します-この場合の計算スキームはマトリックスを超えてしまうため、境界セルを再計算する方法。


フィルタが元の画像の最大および最小輝度内でセルの輝度値を変更するためには、基本方程式で記述されるプロセスは断熱的でなければなりません。 したがって、次の形式のディリクレ境界条件があります。 $$$I（D）= 0$ 。 つまり、境界線をゼロで埋めるだけです。

Fortranアルゴリズムと実装

計算式に基づいて、常に少なくとも2つの2次元配列をメモリに保持する必要があります。最初の配列は元の画像に対応し、2番目の配列はぼやけます。 ガウスフィルターで類推すると、半径のある画像をぼかすことができます $$$t$ ペロンとマリクのフィルターで実行する必要があります $$$\ frac {t} {\ Delta t}$ 画像の完全な再計算の繰り返し。毎回、前のぼかしレイヤーから「元の」レイヤーに画像を置き換えます。
アクションのシーケンスは次のようになります。

1. 画像の幅と高さを決定します（それぞれwとhを呼び出します）。
2. 次元（w + 2）*（h + 2）の2次元配列にメモリを割り当てます（Iを呼び出しましょう）。
3. 次元（w + 2）*（h + 2）の2次元配列にメモリを割り当てます（BlurIを呼び出しましょう）。
4. 配列をゼロで埋めますI = 0;
5. イメージを読み取り、ピクセルデータを配列Iの中心に書き込みます（つまり、1つのゼロ列または行を左、左、右、上、下のままにします）。
6. レベル<t（最初はレベル= 0）になるまで繰り返します。
   
   
   1. ゼロフィールドによるオフセットインデックスを考慮して、 式4に従って配列Iのすべてのセルを再計算します。 私たちは $$$I_ {i、j} ^ {t + 1}$ BlurIであり、 $$$I_ {i、j} ^ {t}$ -私;
   2. Iの画像データをBlurIに置き換えます。
   3. カウンターを増やします。level= level + deltaT、ここでdeltaT-パラメーター、タイムステップ。
   
   
7. BlurI配列のデータから画像を作成して保存します。 これはぼやけた画像です。
8. メモリを解放し、プログラムを終了します。

カラー画像の場合、アクションの原則は保持されますが、再カウントは各チャネルごとに個別に実行する必要があります。

Fortranの実装

実際、アルゴリズムは非常に簡単で、多くの一般的な言語で簡単にプログラムできます。 Fortranでの実装の難しさに出会ったことがあります。長い間、この言語に関する優れたマニュアルや教科書を見つけることができなかったからです。 したがって、この言語の実装をもたらし、誰かに役立つことを期待しています。

奇妙なことに、プログラミングの主な困難は写真を読むことでした。 Fortranには、イメージを操作するための組み込みプロシージャ（「サブルチン」と呼ばれる言語）はありませんが、プロシージャを実装するために必要なものはすべてあります。

多くのグラフィックエディタでも理解されている最も単純な形式は、PGM P5のように思えました。 これは、グレースケール圧縮なしでビットマップビットマップイメージを格納するためのオープン形式です。 単純なASCIIヘッダーがあり、画像自体は一連のシングルバイト（0〜255のグレースケール）の符号なし整数です。 このフォーマットの詳細については、標準自体で直接読むことができます。リンクはソースセクションにあります。

モジュールの形でPGMを操作する手順を設計しましたが、これはメイントピックには当てはまらないため、詳細には分解しません。 ソースコードへのリンクのみを提供します 。 このモジュールは、最大グレー値が255の画像でのみ機能します。

PGMを操作するモジュールを接続し、必要な変数をすべて宣言することにより、プログラムを開始します。

program blur
  use pgmio

  implicit none
  
  double precision, parameter :: t=10.0d0, deltaT=0.2d0, k=10.0d0
  character*(*), parameter :: input='dif_tomography.pgm', output='output.pgm'

  double precision, allocatable :: u(:,:), nu(:,:)
  double precision :: north, south, east, west, level
  integer :: w, h, offset, n, i, j

end program blur

t — , , deltaT — , k — g. Input output — .

w h.

call pgmsize(input, w, h, offset)

Offset , .

input.

allocate(u(0:w+1,0:h+1))
u=0
allocate(nu(w,h))
call pgmread(input, offset, w, h, u, 0, 0)

, , , , u , 0 w+1 , 0 h+1 . .

pgmread w*h , offset ( PGM) u. , u .

, , , , PGM .

.

  level = 0 !  
  do while (level<t)
    do j=1,h
        do i=1,w
            north = u(i-1,j)-u(i,j)
            south = u(i+1,j)-u(i,j)
            east = u(i,j+1)-u(i,j)
            west = u(i,j-1)-u(i,j)
            nu(i,j) = u(i,j) + deltaT*(g(north)*north+g(south)*south+g(east)*east+g(west)*west)
        end do
    end do
    u(1:w,1:h) = nu(1:w,1:h) !   
    level = level + deltaT
  end do

, , Fortran — , — j i. , , - , . , , — , «-».

.

  deallocate(u)

  call pgmwriteheader(output, w, h) 
  call pgmappendbytes(output, nu, 1, 1) 

  deallocate(nu)

pgmwriteheader output PGM P5. pgmappendbytes output nu, , nu 1 . , pgmappendbytes , , , .

g. , 3.

  contains 
      function g(x) result(v)
        implicit none
        double precision, intent(in) :: x
        double precision :: v
        v = 1/(1+(x/k)**2)
      end function g

→

gfortran ( , ):

gfortran pgmio.f90 blur.f90

t.

.



.



.



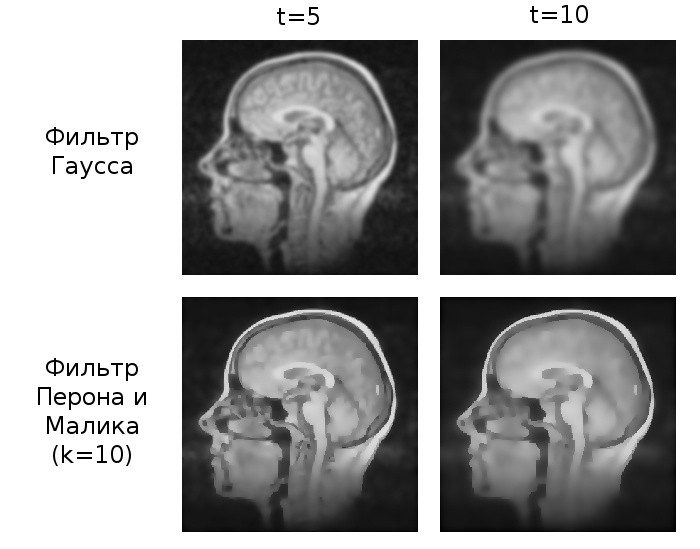
(t=10).



(t=10, k=8).



, .

. k t deltaT (t=10, deltaT=0.2).



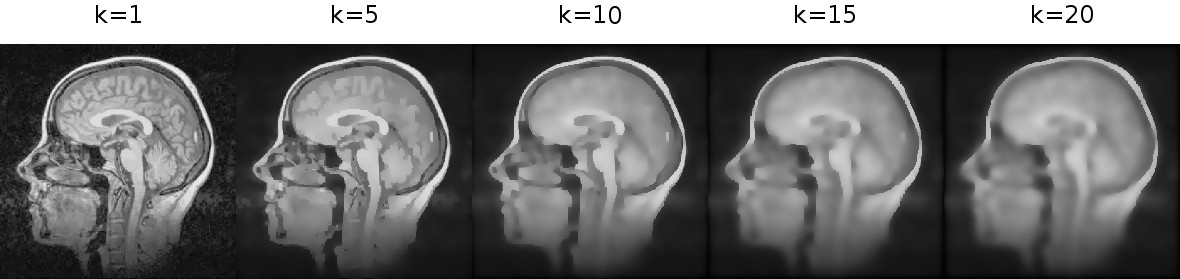
, k. . k , .

(t=10,k=5).



. .



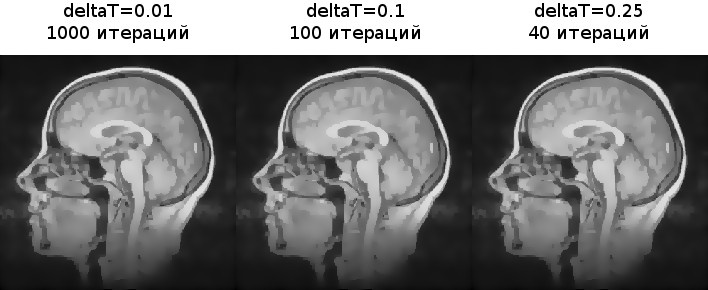
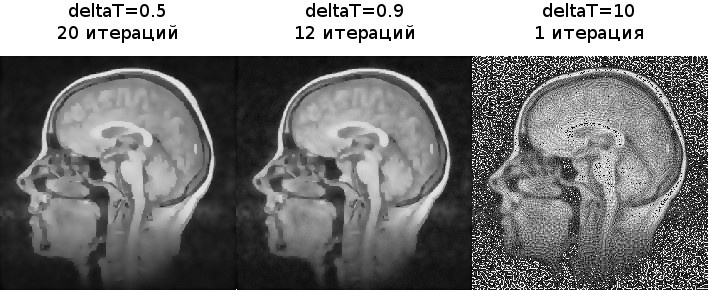
, , . deltaT=10 .

. $$$g$, $$$k$.

, . . , , .

: PGM, .

1. . Scale-Space and Edge Detection Using Anisotropic Diffusion
3. PGM