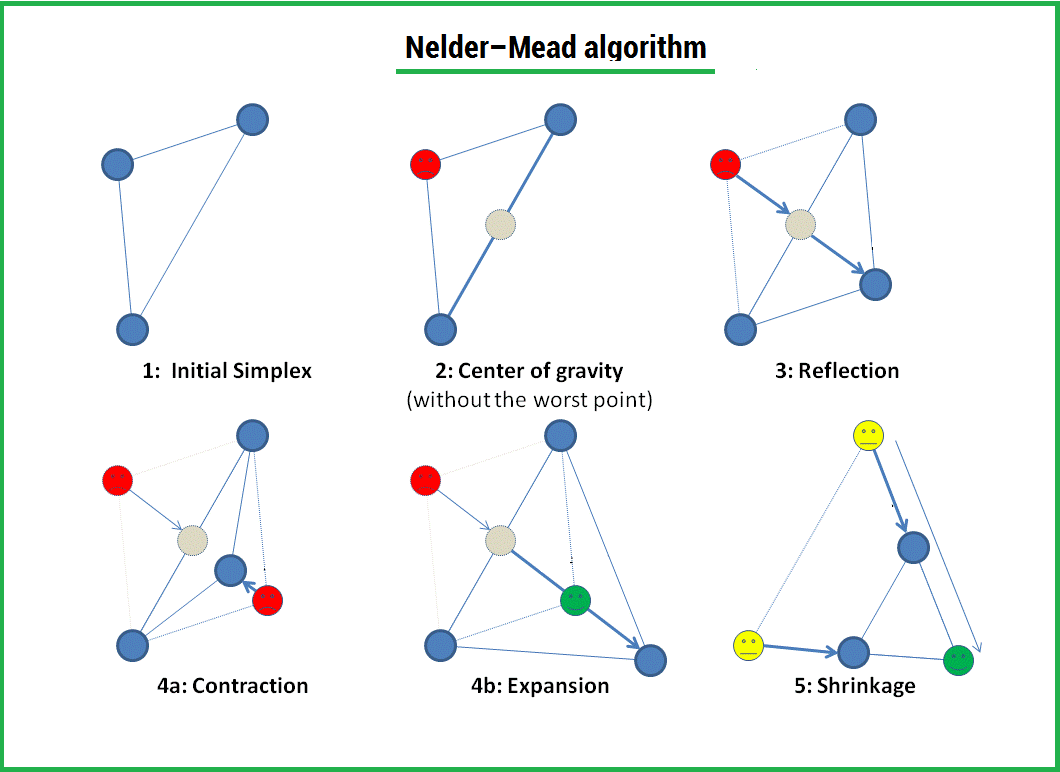
Nelder-Mead最適化方法。 Pythonの実装例

Nelder-Mead法は、いくつかの変数の関数の最適化（最小検索）の方法です。 勾配を使用せずに関数を最適化できる、シンプルで同時に効果的な方法。 収束の理論はありませんが、この方法は信頼性が高く、原則として良好な結果を示します。 数学的計算に使用される一般的なpython言語ライブラリのscipy.optimizeモジュールの最適化関数で使用できます。

このアルゴリズムは、3つの操作を通じて、シンプレックス（ simplex ）の形成と、その後の最小方向への変形で構成されます。

1） 反射 （反射）;
2） ストレッチ （拡張）;
3） 圧縮 （契約）;

シンプレックスは幾何学的図形であり、三角形のn次元の一般化です。 1次元空間の場合、これはセグメントであり、2次元空間の場合、三角形です。 したがって、n次元のシンプレックスにはn + 1の頂点があります。

アルゴリズム

1）させる $$$f（x、y）$最適化される関数。 最初のステップでは、3つのランダムポイントを選択し（これについては後で説明します）、シンプレックス（三角形）を形成します。 各ポイントで関数の値を計算します： $$$f（V_1）$、 $$$f（V_2）$、 $$$f（V_3）$。

関数値でポイントを並べ替える $$$f（x、y）$これらの点で、したがって二重の不等式が得られます。 $$$f（V_2）\ leq f（V_1）\ leq f（V_3）。$

関数の最小値を探しているため、このステップでは、関数の値が最小になる点が最良のポイントになります。 便宜上、次のようにポイントを再指定します。

b = $$$V_2$、g = $$$V_1$、w = $$$V_3$どこが最高、良い、最悪-それぞれ。



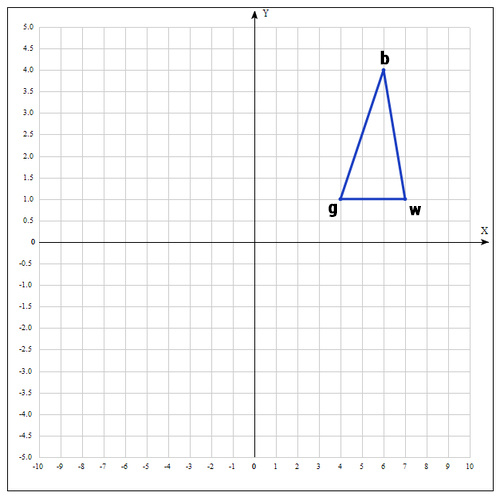
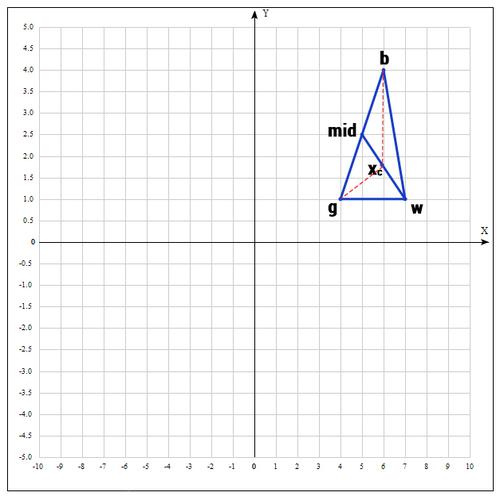
2）次のステップで、ポイントがgとbであるセグメントの中央を見つけます。 なぜなら セグメントの中央の座標は、その端の座標の半和に等しくなります。

$$

$$mid = \左（\ frac {x_1 + x_2} 2; \ frac {y_1 + y_2} 2 \右）$$

より一般的な形式では、これを書くことができます：

$$

$$mid = \ frac 1 n \ sum_ {i = 1} ^ n x_i$$

3）リフレクション操作を適用します。
ポイントを見つける $$$x_r$次のように：

$$

$$x_r = mid +α（mid-w）$$

すなわち 実際には、中点に対する点wを反映します。 原則として、ルール1を採用します。 $$$f（x_r）<f（g）$これは良い点です。 そして、距離を2倍に増やしてみましょう。突然ラッキーになり、ポイントがさらに良くなります。



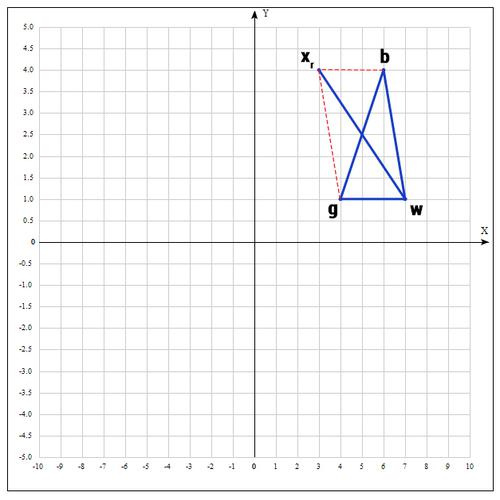
4）ストレッチの操作を適用します。
ポイントを見つける $$$x_e$次のように：

$$

$$x_e = mid +γ（x_r-mid）$$

γとしてγ= 2を使用します。 距離は2倍に増加します。

チェックポイント $$$x_e$：

もし $$$f（x_e）<f（b）$、それから私たちは幸運だったと私たちはそれが今よりも良い点を見つけた、これが起こらなかった場合、私たちは点で停止します $$$x_r$。

次に、点wを $$$x_e$、最終的に次のようになります：



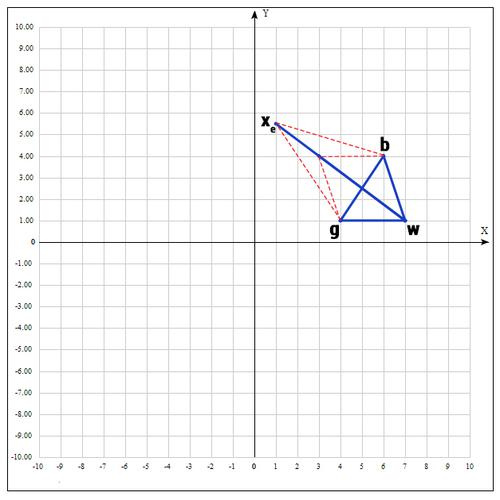
5）まったく運が良くなく、良い点が見つからなかった場合は、圧縮操作を試みます。
操作の名前が示すように、セグメントを縮小し、三角形内の適切なポイントを探します。

良い点を見つけようとする $$$x_c$：

$$

$$x_c = mid +β（w-mid）$$

係数βは0.5に等しく、つまり ポイント $$$x_c$wmidセグメントの中央。



別の操作があります-縮小（縮小）。 この場合、シンプレックス全体を再定義します。 「最良の」ポイントのみを残し、残りは次のように決定されます。

$$

$$x_j = b +δ（x_j-b）$$

係数δは0.5に等しくなります。

基本的に、現在の「最良の」ポイントに向かってポイントを移動します。 変換は次のとおりです。



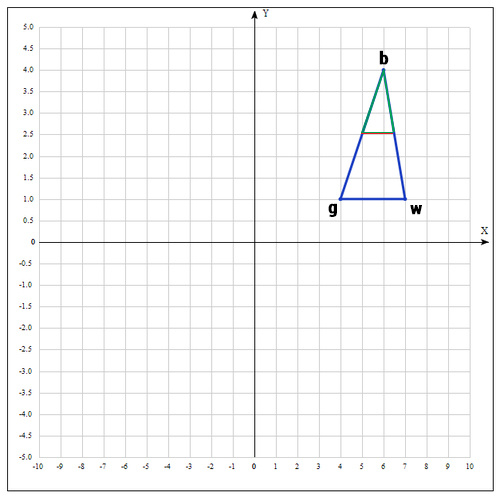
シンプレックス内のポイントを置き換える必要があるため、この操作は高価であることに注意してください。 幸いなことに、実際に収縮変換が起こることはめったにないことが多くの実験で発見されました。

アルゴリズムは次の場合に終了します。

1）必要な反復回数が実行されました。
2）シンプレックスの面積が特定の値に達しました。
3）現在の最適なソリューションは、必要な精度に達しました。

ほとんどのヒューリスティック手法と同様に、初期化ポイントを選択する理想的な方法はありません。 既に述べたように、シンプレックスを形成するために、互いに近くにあるランダムなポイントを取ることができます。 しかし、MATLABのアルゴリズムの実装で使用されるより良いソリューションがあります。

最初のポイントの選択 $$$V_1$ユーザーに適切な解決策のアイデアがある場合はユーザーに委任します。そうでない場合はランダムに選択されます。 残りのポイントは、に基づいて選択されます $$$V_1$、各測定の方向に沿ってわずかな距離で：

$$

$$V_ {i + 1} = V_i + h（V_1、i）* U_i$$

どこで $$$U_i$単位ベクトルです。
$$$h（V_1、i）$このように定義されます：
$$$h（V_1、i）$=係数が $$$U_i$定義で $$$V_1$ゼロではありません。
$$$h（V_1、i）$= 0.00025、係数が $$$U_i$ゼロの定義で。

例：

次の関数の極値を見つけます。 $$$f（x、y）= x ^ 2 + xy + y ^ 2-6x-9y$

出発点として、次の点を取ります。

$$

$$V_1（0、0）、V_2（1、0）、V_3（0、1）$$

各ポイントで関数の値を計算します：

$$

$$f（V_1）= f（0、0）= 0$$

$$

$$f（V_2）= f（1,0）= -5$$

$$

$$f（V_3）= f（0、1）= -8$$

次のようにポイントの名前を変更します。

$$

$$b = V_3（0、1）、g = V_2（1、0）、w = V_1（0、0）$$

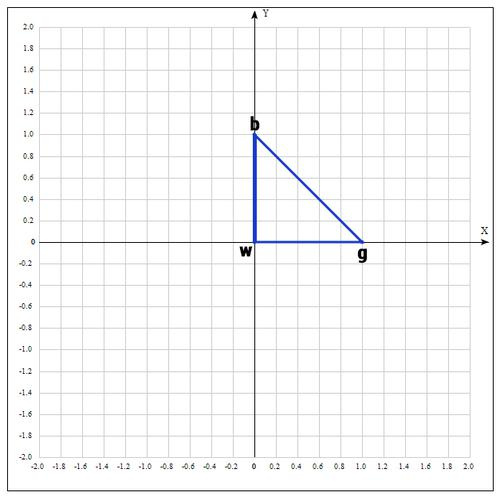
セグメントbgの中央を見つけます。

$$

$$mid = \ frac {b + g} 2 = \左（\ frac 1 2; \ frac 1 2 \右）$$

ポイントを見つける $$$x_r$（反射操作）：

$$

$$x_r = mid +α（mid-w）、$$

α= 1の場合：

$$

$$x_r = 2 * mid-w = 2 \ left（\ frac 1 2; \ frac 1 2 \ right）-\ left（0、0 \ right）=（1、1）$$

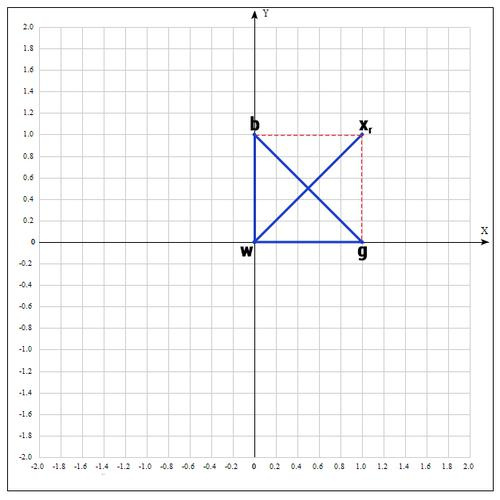
チェックポイント $$$x_r$：

$$$f（x_r）= -12$なぜなら $$$f（x_r）<f（b）$セグメントを増やしてみてください（操作のストレッチング）。

$$

$$x_e = mid +γ（x_r-mid）、$$

γ= 2の場合：

$$

$$x_e = 2x_r-ミッド$$

$$

$$x_e = 2（1、1）-\左（\ frac 1 2、\ frac 1 2 \右）=（1.5、1.5）$$

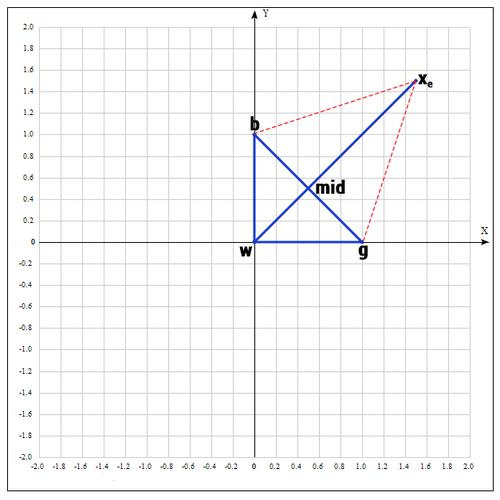
その時点で関数の値を確認してください $$$x_e$：

$$

$$f（x_e）= f（1.5、1.5）= -15.75$$

ポイントが判明した $$$x_e$ポイントbよりも「良い」。 したがって、新しい頂点を取得します。

$$

$$V_1（1.5、1.5）、V_2（1、0）、V_3（0、1）$$

そして、アルゴリズムは最初からやり直します。

10回の反復の値の表：

最高	いいね	最悪
$$$f（0、1）= -8$	$$$f（1.0、0）= -5$	$$$f（0、0）= 0$
$$$f（1.5、1.5）= -15.75$	$$$f（0、1）= -8$	$$$f（1.0、0）= -5$
$$$f（0.25、3.75）= -20.187$	$$$f（1.5、1.5）= -15.75$	$$$f（0、1）= -8$
$$$f（0.25、3.75）= -20.187$	$$$f（1.75、4.25）= -20.1875$	$$$f（1.5、1.5）= -15.75$
$$$f（1.125、3.375）= -20.671$	$$$f（1.75、4.25）= -20.1875$	$$$f（0.25、3.75）= -20.1875$
$$$f（1.140、3.796）= -20.9638$	$$$f（1.125、3.375）= -20.6718$	$$$f（1.75、4.25）= -20.1875$
$$$f（1.140、3.796）= -20.9638$	$$$f（1.287、3.751）= -20.8668$	$$$f（1.125、3.375）= -20.6718$
$$$f（1.140、3.796）= -20.9638$	$$$f（1.236、3.874）= -20.9521$	$$$f（1.287、3.751）= -20.8668$
$$$f（0.990、4.002）= -20.9951$	$$$f（1.140、3.796）= -20.9638$	$$$f（1.2365、3.874）= -20.9520$
$$$f（0.990、4.002）= -20.9951$	$$$f（0.895、3.925）= -20.9855$	$$$f（1.140、3.796）= -20.9638$

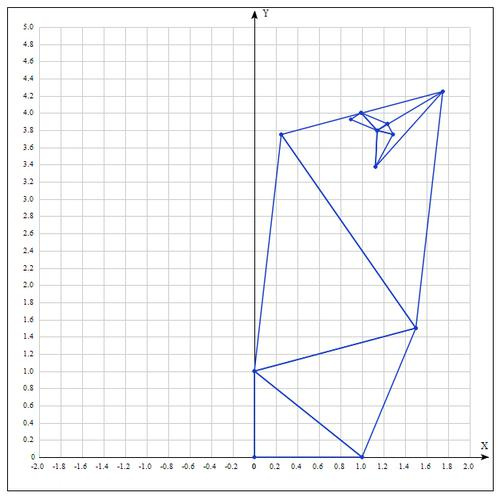
関数の極値を分析的に見つけます;ポイントに到達します $$$f（1、4）= -21$。
10回の反復後、かなり正確な近似が得られます。 $$$f（0.990、4.002）= -20.999916$

メソッドの詳細：

Nelder-Meadアルゴリズムは、主に機械学習のパラメーターを選択するために使用されます。 本質的に、シンプレックス法はモデルパラメーターを最適化するために使用されます。 これは、この方法が目的関数をかなり迅速かつ効率的に最適化するという事実によるものです（特に縮小が使用されていない場合-変更）。

一方、収束の理論が欠如しているため、実際には、この方法は、滑らかな（連続的に微分可能な）関数であっても誤った答えを導きます。 また、機能するシンプレックスが最適点から遠く離れている可能性があり、アルゴリズムは、関数をわずかに変更しながら多数の反復を実行します。 この問題を解決するためのヒューリスティックな方法は、アルゴリズムを数回実行し、反復回数を制限することです。

Pythonプログラミング言語での実装：

補助クラスVectorを作成し、演算子をオーバーロードして、ベクターで基本的な操作を実行できるようにします。 私は意図的に補助ライブラリを使用してアルゴリズムを実装しませんでした。 この場合、知覚はしばしば低下します。

#!/usr/bin/python # -*- coding: utf-8 -*- class Vector(object): def __init__(self, x, y): """ Create a vector, example: v = Vector(1,2) """ self.x = x self.y = y def __repr__(self): return "({0}, {1})".format(self.x, self.y) def __add__(self, other): x = self.x + other.x y = self.y + other.y return Vector(x, y) def __sub__(self, other): x = self.x - other.x y = self.y - other.y return Vector(x, y) def __rmul__(self, other): x = self.x * other y = self.y * other return Vector(x, y) def __truediv__(self, other): x = self.x / other y = self.y / other return Vector(x, y) def c(self): return (self.x, self.y) # objective function def f(point): x, y = point return x**2 + x*y + y**2 - 6*x - 9*y def nelder_mead(alpha=1, beta=0.5, gamma=2, maxiter=10): # initialization v1 = Vector(0, 0) v2 = Vector(1.0, 0) v3 = Vector(0, 1) for i in range(maxiter): adict = {v1:f(v1.c()), v2:f(v2.c()), v3:f(v3.c())} points = sorted(adict.items(), key=lambda x: x[1]) b = points[0][0] g = points[1][0] w = points[2][0] mid = (g + b)/2 # reflection xr = mid + alpha * (mid - w) if f(xr.c()) < f(gc()): w = xr else: if f(xr.c()) < f(wc()): w = xr c = (w + mid)/2 if f(cc()) < f(wc()): w = c if f(xr.c()) < f(bc()): # expansion xe = mid + gamma * (xr - mid) if f(xe.c()) < f(xr.c()): w = xe else: w = xr if f(xr.c()) > f(gc()): # contraction xc = mid + beta * (w - mid) if f(xc.c()) < f(wc()): w = xc # update points v1 = w v2 = g v3 = b return b print("Result of Nelder-Mead algorithm: ") xk = nelder_mead() print("Best poits is: %s"%(xk)) 

記事を読んでくれてありがとう。 彼女があなたにとって有益であり、あなたが多くを学んだことを願っています。
FUNNYDMANはあなたと一緒でした。 最適化！）