ジュリア・フィリモノワとのコラボレーション。
はじめに
そのような勝者全体が基地に飛んで、爆弾がなく、何もトラブルを前兆にしないと想像してください...

そして、ここで、たとえば、雲/雲の小さな霧が予期せずに表示されるか、またはそれが多少悪くなります-これ...そして、あなたは歓迎されますが、目標としてのみ:

#poralize-しかし、今では数学的なバイアスでそれをどのように行うのか、今は理解できます。
そして、一般的には、例えばYandexで言われているように、予期せず遭遇した障害物/障害物を回避する必要がある場合が多くあります。
数学者の予約。 , . : - , , , .
パート1-「単純な動き」のモデル
単純な動きは、ポップシンギングだけでなく、動的オブジェクトの最も単純なモデルであり、次の差分モデルで表されます。
$$表示$$ \ドットx = u、\ x(t_0)= x_0、$$表示$$
どこで $ inline $ x(t)\ in R ^ n \ u \ in P \サブセットR ^ n $ inline $ 、-control limited $ inline $ P:| u | <c_u $ inline $ (速度は無限ではないため、論理的です)、および $インライン$ R ^ n $インライン$ - $インライン$ n $インライン$ 次元ユークリッド空間(この例では、ご覧のとおり、2次元で十分です)。 多くの $インライン$ M $インライン$ -私たちのベース、すなわち ここで私たちは安全で健全な状態に戻したいと思っています $インライン$ x_1 $インライン$ 。
これにより何が得られますか? 方程式を積分すると、運動の軌跡、つまり直線が得られます $インライン$ x(t)= ut + C $インライン$ 、つまり、管理が指示されている場合は、そこに飛びます。 したがって、干渉がない場合、制御ベクトル $インライン$ u $インライン$ 動きベクトルと整列 $インライン$ x_1-x_0 $インライン$ 。
このモデルのプラスは、分析の極度のシンプルさ、マイナスです-慣性のない動きのみをモデル化しますが、慣性の動きのモデリングは次のようになる(単純化される)ので、それほど怖くはありません:
$$表示$$ \ ddot x = u \右矢印\左\ {\ begin {array} {rcl} \ dot x_1&=&x_2 \\ \ dot x_2&=&u。 \ end {array} \ right。$$表示$$
そして、対応するタイプのモデルに少し後で進みます。
説明したモデルは、動的な機能を反映しています。 敵を追加する $インライン$ v $インライン$ 可能な限りの方法で私たちを妨げようとする人:
$$表示$$ \ドットx = u-v、\、x(t_0)= x_0、\、\存在T:x(T)\ in M、\、\ forall t <T:x(t)\ notin N、\、u \ in P \サブセットR ^ n、\、v \ in Q \サブセットR ^ n $$ display $$
ここでは、同様に制限された管理 $インライン$ Q:| v | <c_v $インライン$ 。
同時に、敵がどこに隠れているかを事前に知ることはできませんが、同時に、彼はすべてを知っており、私たちが近くを飛ぶ間、自分を待っているので、彼のコントロールの助けを借りて $インライン$ v $インライン$ 私たちをたくさん手に入れてください $インライン$ n $インライン$ 。
私たちの目標は $インライン$ M $インライン$ かわすことを保証 $インライン$ n $インライン$ 、実際に何を回避しているのかを知る必要があり、遅かれ早かれ障害を見つけます。 慣性のない動きの場合、最後から2番目の瞬間まで何もわからない場合があります。この場合、速度ベクトル(および、それに応じて軌道)を干渉から常に遠ざけることができるからです。
同時に、ご覧のとおり、<<山>>型の干渉は、大きな障害ではありますが動かないため、最悪の状況ではありません。敵が機動している場合はさらに悪いので、さらにいくつかの点を議論する必要があります。
- 回避するには、敵よりも大きな動的能力が必要です。そうでなければ、遅かれ早かれ彼らは私たちを捕まえます。 $インライン$ Q $インライン$ ある意味では少ないはずです $インライン$ P $インライン$ ;
- 敵によって制御される障害物のセットを凸面にします;そうでなければ、障害物のセットから法線を回避する戦略を適用する場合 $インライン$ n $インライン$ -回避できません。
上記のヒューリスティックな引数を使用して、空間内の次の条件下で上記の問題を解決する方法を確認します。 $インライン$ R ^ 2 $インライン$ :
$$ display $$ \ begin {array} {rcl} \ dot {x} _1&=&u_1-v_1、\\ \ dot {x} _2&=&u_2-v_2。 \ end {array} $$表示$$
ここに $インライン$ x_1、\ x_2 $インライン$ -オブジェクトの座標 $インライン$ x $インライン$ 飛行機で $インライン$ x(t)= [x_1(t)、\ x_2(t)] ^ {T} \ in \ mathbb {R} ^ 2. $ inline $
オブジェクトが点から動き始める $ inline $ x(t_0)= [3、\ 4] ^ {T} \ in \ mathbb {R} ^ 2. $ inline $
管理制限 $インライン$ u(t)、\ v(t)$インライン$ 形がある
- $インライン$ u(t)\ in P \サブセット\ mathbb {R} ^ 2、\ P = S_ {1}([0、\ 0] ^ {T})$ inline $ -半径1の円;
- $インライン$ v(t)\ in Q \サブセット\ mathbb {R} ^ 2、\ Q = S_ {0.9}([0、\ 0] ^ {T})$ inline $ -半径0.9の円。
最初のプレーヤーは、システムの軌跡を有限時間で端末セットに転送しようとします $インライン$ M = S_ {1}([12、\ 6] ^ {T})$インライン$ -点を中心とする半径1の円 $インライン$ [12、\ 6] ^ {T} $インライン$ 複数の干渉を回避しながら $インライン$ N = S_ {2}([8、\ 5] ^ {T})$インライン$ -点を中心とする半径2の円 $インライン$ [8、\ 5] ^ {T} $インライン$ 。
最初のプレイヤーがゲームを正常に完了する時間 $インライン$ T = 36.0 $インライン$ 。
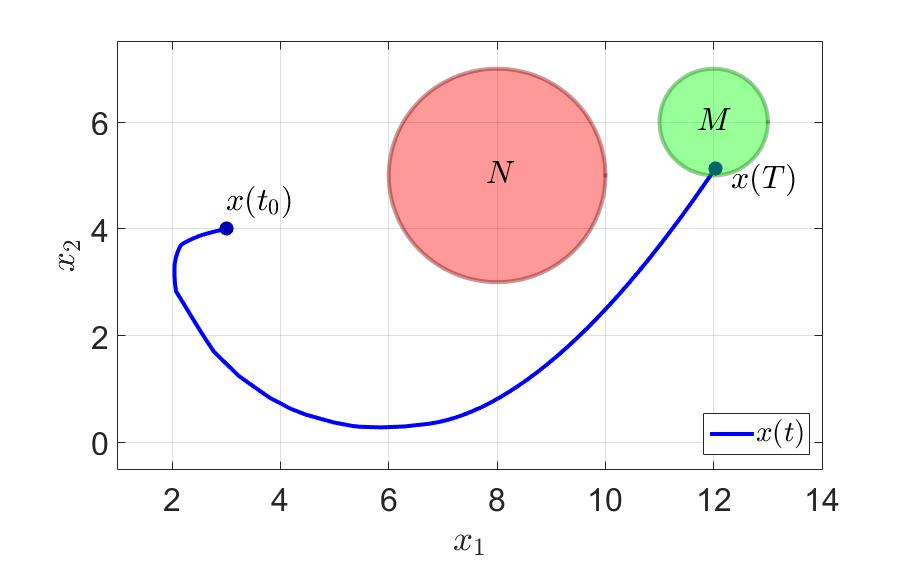
システムの軌跡と最初のプレーヤーのコントロールを次の図に示します。
システムの軌跡。 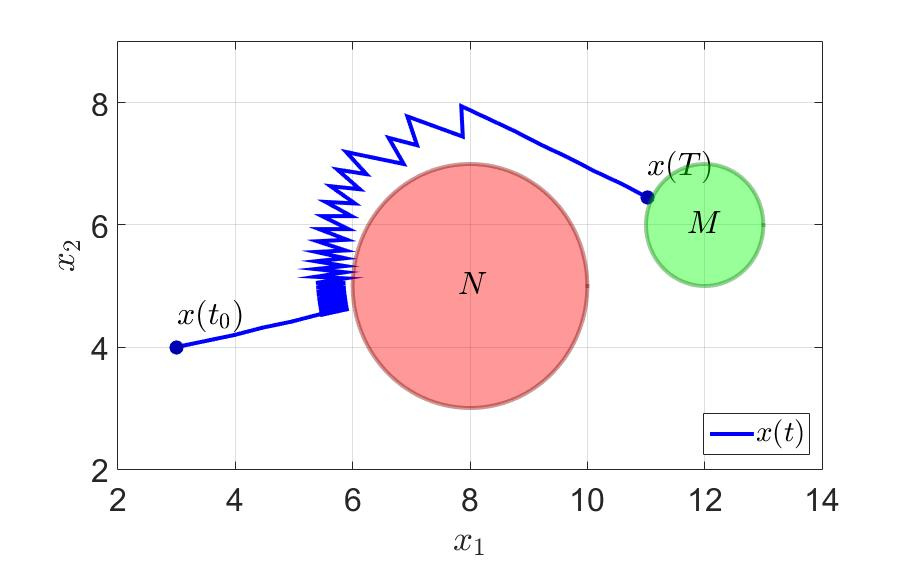
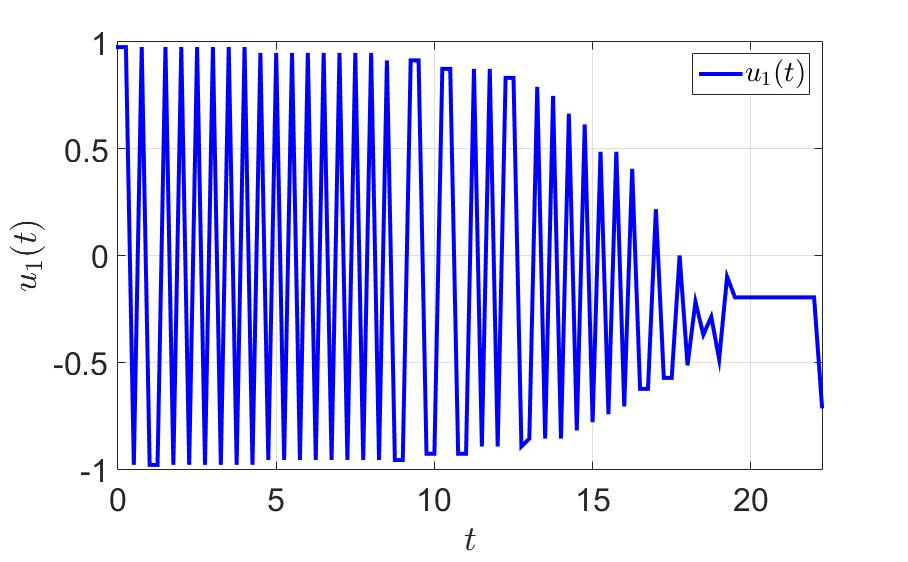
最初の制御コンポーネントの時間依存性。 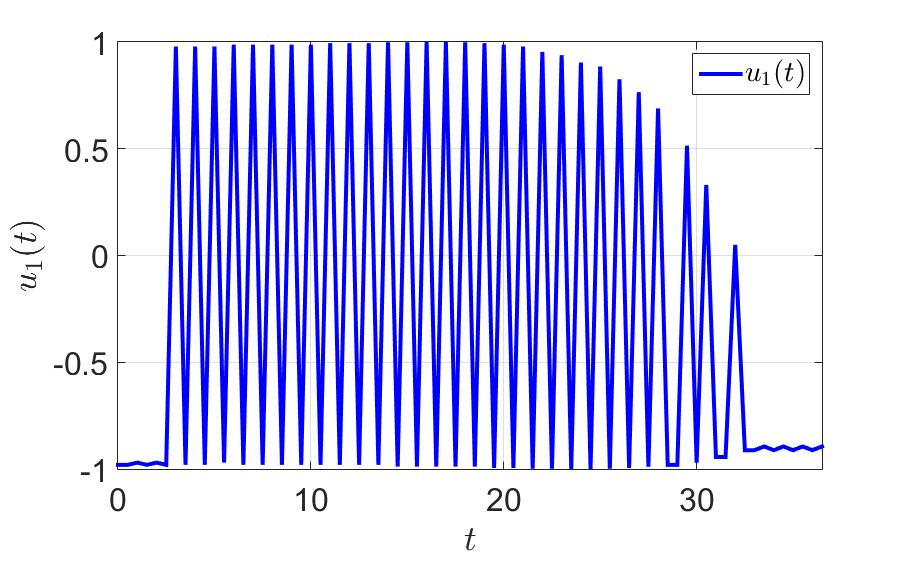
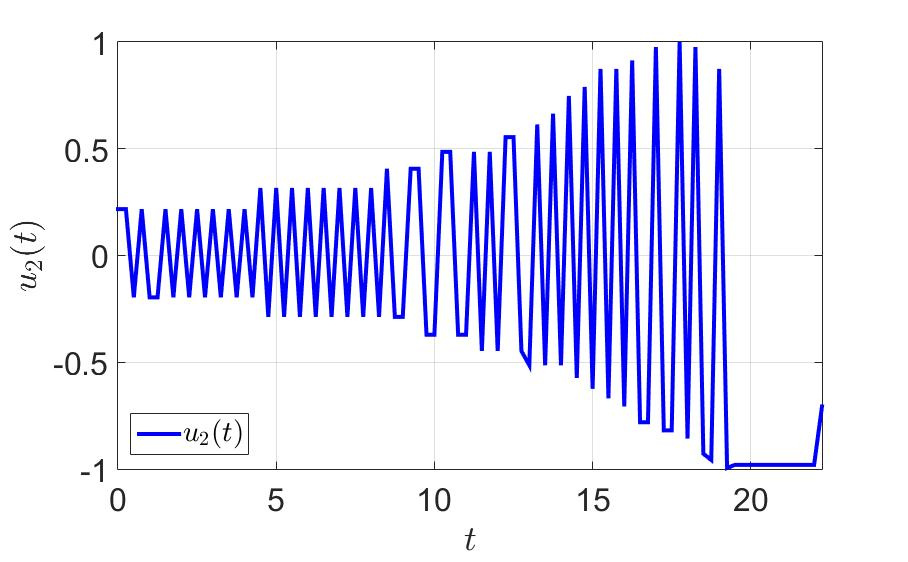
2番目の制御コンポーネントの時間依存性。 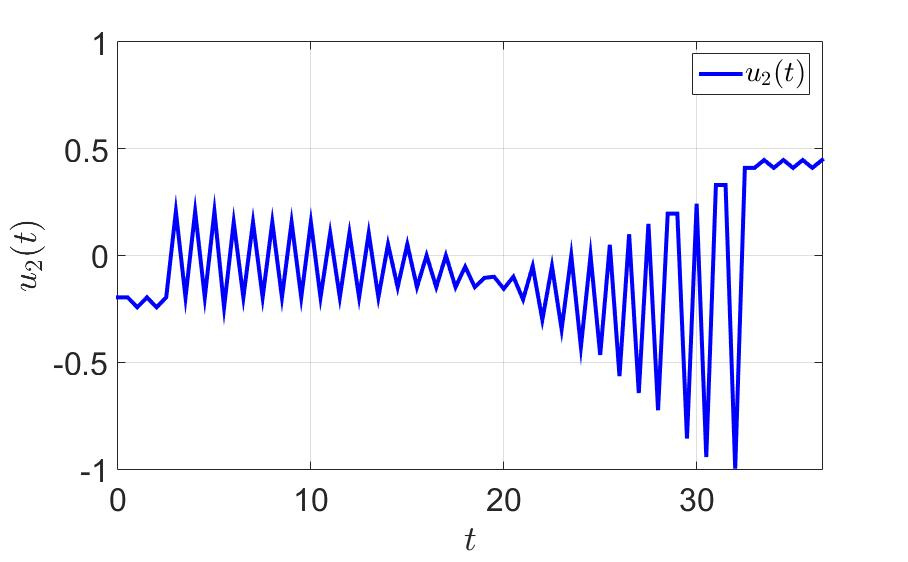
このアプローチには、明らかにいくつかの欠点があります。
- 極端な値の間のジャークがコントロールに大きな負荷を与えるため、実用的な観点からは多数のスイッチ。
- その結果、ターゲットに向かって飛行するのではなく、干渉を回避して端末セットを指すように歩き回ります。
- 厳密に通常の干渉まで飛ぶ場合の対処方法は明確ではありません。回避は、その前のステップを指していたのと同じポイントで実行されます。つまり、アルゴリズムがループする可能性があります。
- ヒューリスティックはもちろん良いので、慣性オブジェクトをどうするかは明確ではありませんが、現実はやや複雑です。
パート2-モデルは「単純な動作」のままですが、スイッチの数は減ります
モデルは単純であり、平面に沿って任意のポイントから任意のポイントに移動できるため(これは将来の重要な仮定ですが、現時点ではメモを取るだけです)、次のように推論することを妨げるものはありません。
一歩先を考えてみましょう:システムが最初にターゲットに向けられ、次のステップで逸脱し始めた場合、システムが2つのステップで到達し、すぐにそれを中間ターゲットとして指すポイントを見つけることができます。 できますか 私たちの仮定-はい。
同じ例で、何が起こるか見てみましょう。 最初のプレイヤーがゲームを正常に完了した時間は、 $インライン$ T = 36.0 $インライン$ 前に $インライン$ T = 11.5 $インライン$ 。 切り替え回数も大幅に減少しました。 注意してください-少なくとも一歩先を効果的に考えてください そして一般的に健康に良い 。
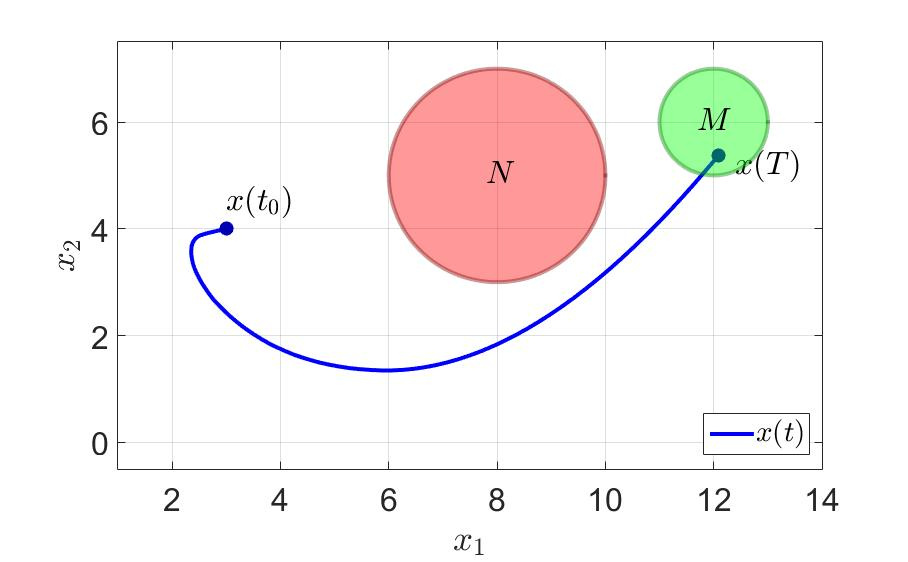
システムの軌跡と最初のプレーヤーの制御コンポーネントを次の図に示します。
システムの軌跡。 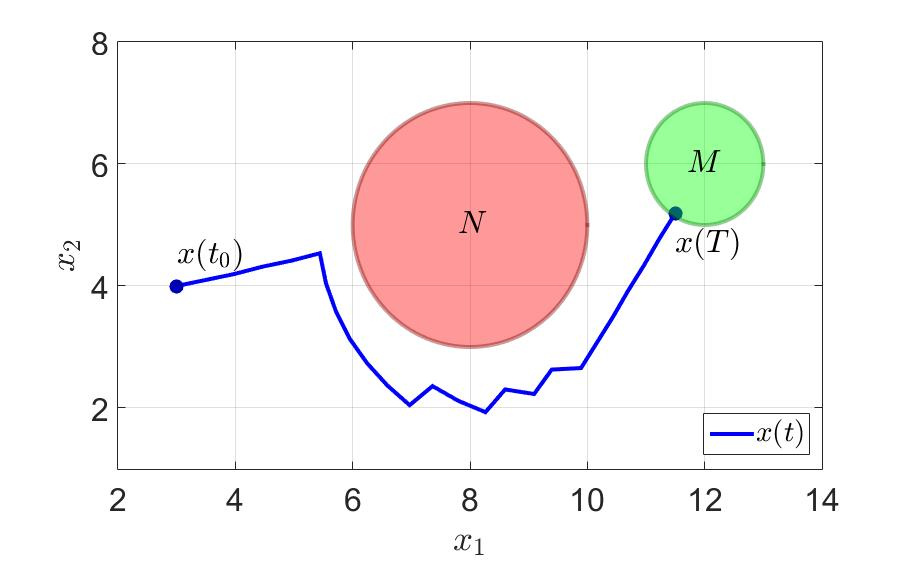
最初の制御コンポーネントの時間依存性。 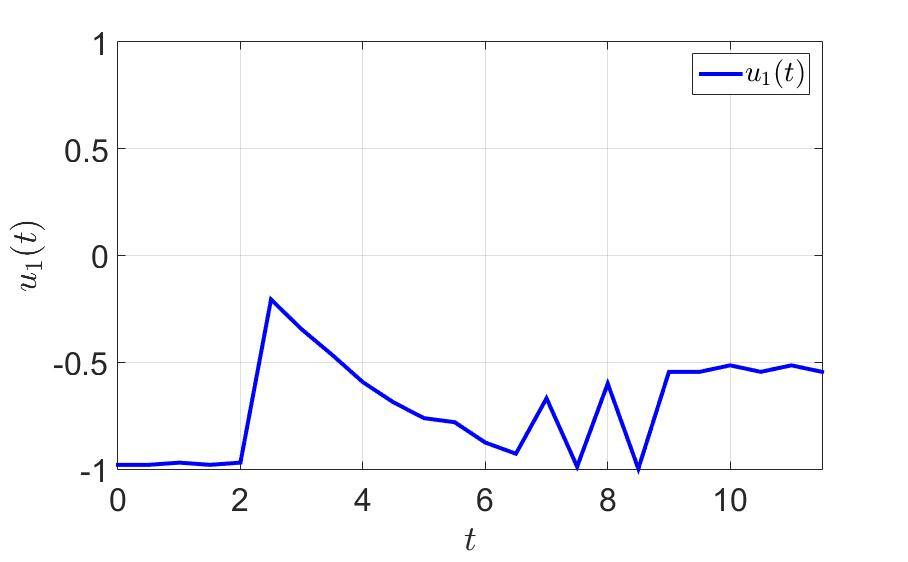
2番目の制御コンポーネントの時間依存性。 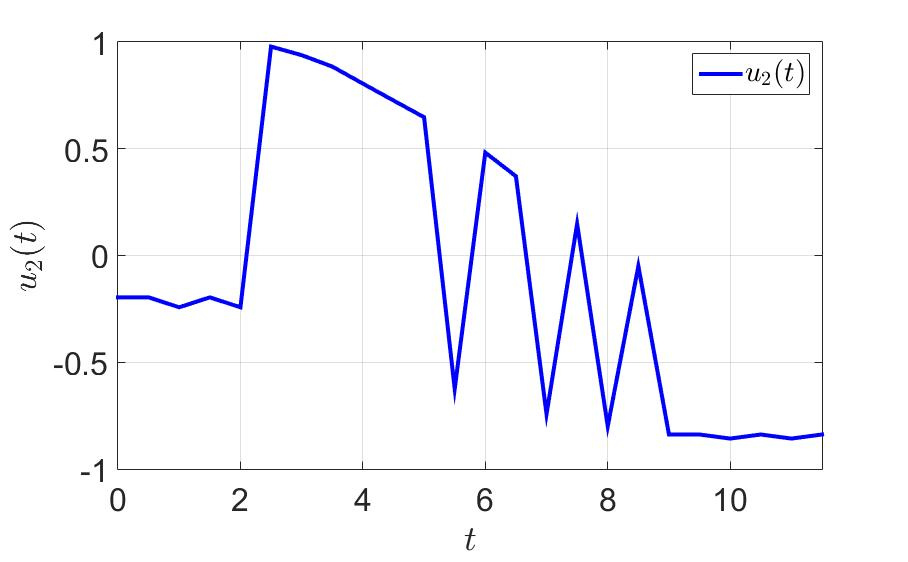
パート3-モデルはまだ「単純な動き」にありますが、ここで<< normal >>の近似で問題を解決します
一度に1つのセットを回避できるため、追加のセットを構築することを妨げるものは何もありません。それを回避し、(おそらく時間ステップの改良を加えて)それとは異なるポイントに到達することが保証されます。私たちが今いるところ。 そして、次のようにします。
軌道の追加の回避セットの構築。
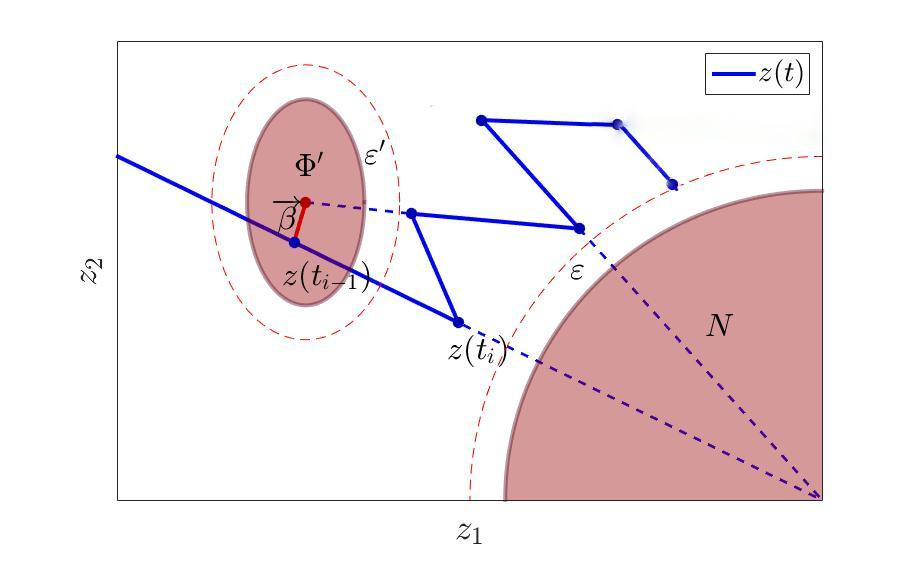
つまり、追加のセットを作成するだけで、そこから「問題」ポイントを中心としてではなく、図のようにいくらかの変位を含めて回避します。
パート4-数学的基礎
それでも、慣性オブジェクトの制御を構築するには、理論に没頭する必要があります。この場合、単純なヒューリスティックな議論が機能しなくなり、それに応じて、ソリューションの理論的根拠を選択する必要があるからです。 もしあなたが 重度の怠laz 十分な時間がない場合は、セクションをスキップして結果をすぐに使用できます。興味がある場合は、さらに調べてください。
基礎として、Lev Semenovich Pontryagin [1]によってわが国で開発された微分ゲームの理論を使用します(それが誰であるかわからない場合は、必ず読んでください。 。
これを解決するには、2つのセットが必要です。
- 最初のプレーヤーを取得できる場所-最初のプレーヤーの到達可能性。
- 最初のプレイヤーの2番目のプレイヤーの追跡を完了することができます。
同様に、それらの構築方法、実際に実装されています。
最初のセットでは、干渉がない場合、有限セットを含むように構築できるかどうかは多かれ少なかれ明確です $インライン$ M $インライン$ -それはゲームが正常に完了することを意味します、私たちはできません-それはゲームが単に完了できないことを意味します。 理論的には、次のように構築されます-初期から始まる各ポイント $インライン$ x_0 $インライン$ 利用可能なすべてのコントロールを列挙することにより、取得できるセットを構築します $インライン$ \デルタt $インライン$ 、その後操作を繰り返します。 複雑に見えますが、凸集合と線形システムの場合、凸解析装置を使用してすべてを根本的に簡素化できます。サポート関数と対応するグリッドの導入[4]。 このようなセットの構築は、最初のプレイヤーを指す問題を解決します。それをタスクAと呼びましょう。
干渉なしで多くの$ M $を目指して 。 
2番目のセット(2番目のプレイヤーが私たちを捕まえることができ、回避する必要があるセット)については、それはやや複雑です-指を見てください:
- 一方で、敵を「アプローチ」する場合、能力の優位性を考慮して、敵から遠ざかるほど捕まえる可能性が高くなります。これには厳密な説明が必要になります。
- 一方、敵から「遠ざかる」場合、その優位性を考慮して、敵はどのような場合でも私たちを捕まえることができません。
つまり、逸脱するセットは、一方で(接近するとき)大きくなり、アークの反対側(離れるとき)で避ける必要があるものよりもわずかに大きくなる可能性があります。
群衆の回避 $インライン$ n $インライン$ 。 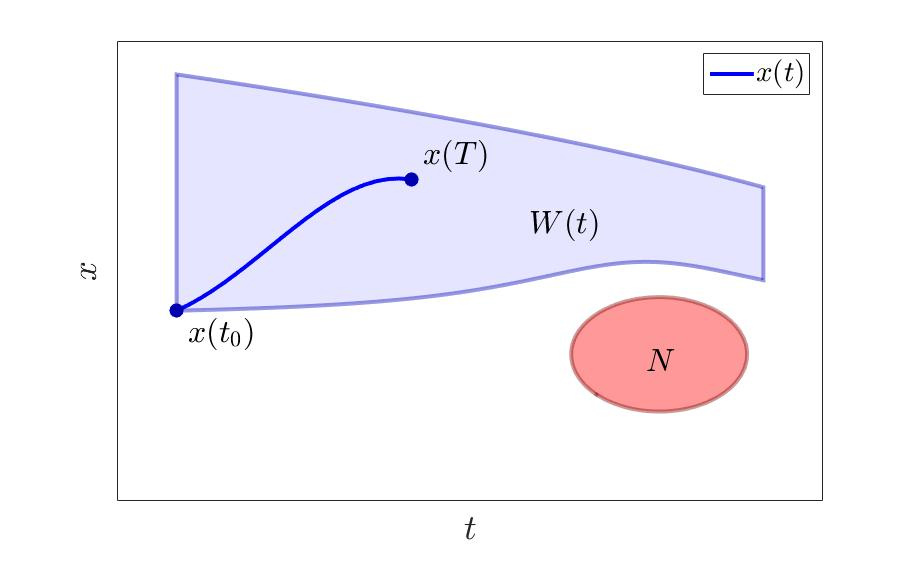
偶然? 論争? そうは思いません 「Back to the Future」の「時空連続体」のDocのように、もう1つの変数があることを思い出してください-時間であり、引用符で引用された「接近」および「移動」という用語は、軌跡に沿ったシステムの動作として解釈されます直線運動と一致し、ユークリッド空間の距離によって特徴付けられることは確かではありません。 しかし、特定のポイントに移動する間、「遠近」および「近づいてくる」という概念は非常によく特徴付けられています。
この場合、回避する必要があるセットからではなく、回避のコントロールを構築しましょう $インライン$ n $インライン$ 、セット内の対応する時間間隔に近づくまでに、変換後のセットから(最初のプレイヤーの優位性により減少します) $インライン$ n $インライン$ -つまり 狭い側面を持つ最初のプレーヤーに向けられた一種のファンネルを構築し、それからすでに始めます。 ゲームのすべての瞬間にそのようなセットを構築し、それを回避することで、最初のプレイヤーを回避する問題を解決します。それを問題Bと呼びましょう。
したがって、一般的な管理は最初のプレーヤーの管理であるため、各時点でこれらのサブタスクの1つだけを解決します。
次に、オブジェクトの動きを形式化します $インライン$ x $インライン$ で $インライン$ x $インライン$ -次元ユークリッド空間 $インライン$ \ mathbb {R} ^ n $インライン$ 次の微分方程式系:
$$表示$$ \ドット{x} = A x + B u-C v、$$表示$$
どこで $ inline $ x \ in \ mathbb {R} ^ n、\ u \ in P \サブセット\ mathbb {R} ^ p、\ v \ in Q \サブセット\ mathbb {R} ^ q $ inline $ ; $インライン$ P、\ Q $インライン$ -ユークリッド空間からの凸コンパクト集合 $ inline $ \ mathbb {R} ^ p、\ \ mathbb {R} ^ q $ inline $ ; $インライン$ A、\ B、\ C $インライン$ -定数行列、 $ inline $ A \ in \ mathbb {R} ^ {n \ times n}、\ B \ in \ mathbb {R} ^ {n \ times p}、\ C \ in \ mathbb {R} ^ {n \ times q} $インライン$ 、すべての存在、一意性、継続性を保証します $インライン$ t \ ge t_0 $インライン$ コーシー問題の解決策。
ベクトル $インライン$ u $インライン$ 最初のプレイヤー、ベクターが自由に使える $インライン$ v $インライン$ 2番目のプレイヤーが自由に使用できます。
運動は $インライン$ t = t_0 $インライン$ 初期状態から $インライン$(x_0、\ t_0)$インライン$ ルベーグの測定可能な機能の影響下で進行する $ inline $ u(t)\ in P、\ v(t)\ in Q $ inline $ 。
で $インライン$ \ mathbb {R} ^ n $インライン$ いくつかの空でない凸閉集合は区別されます $インライン$ M $インライン$ そして $インライン$ n $インライン$ 。 多くの $インライン$ M $インライン$ 最初のプレーヤーの端末セットです。 最初のプレイヤーの目標は、インクルージョンを達成することです $ inline $ x(t_1)\ in M $ inline $ いくつかのために $インライン$ t_1 \ ge t_0 $インライン$ 。 多くの $インライン$ n $インライン$ 2番目のプレーヤーの端末セットと1番目のプレーヤーの干渉セットです。 2番目のプレーヤーの目標は、インクルージョンを達成することです $ inline $ x(t_1 ')\ in N $ inline $ いくつかのために $インライン$ t_1 '\ ge t_0 $インライン$ 。 ポイントの最初のヒットの瞬間に $インライン$ x(t)$インライン$ に $インライン$ n $インライン$ ゲームは2番目のプレーヤーによって正常に完了したと見なされます。 最初のプレーヤーの追加のタスクは、ポイントを打つことを避けることです $インライン$ x(t)$インライン$ に $インライン$ n $インライン$ 。
ゲームは、ポイントの最初のヒット時に最初のプレーヤーによって正常に完了したと見なされます $インライン$ x(t)$インライン$ に $インライン$ M $インライン$ 過去のすべての時点でポイントが $インライン$ x(t)$インライン$ ヒットしない $インライン$ n $インライン$ 。 したがって、プレイヤーの目標は一致せず、ポイント $インライン$ x(t)$インライン$ 戦う部門の影響を受けている $インライン$ u(t)、\ v(t)$インライン$ 。
差分ゲームについては、第1プレイヤーと第2プレイヤーの観点から個別に検討します。
A:最初のプレイヤーが知っていることを前提としています:
- 競合する管理対象エンティティの動的機能 $インライン$ x $インライン$ 、つまり行列 $インライン$ A、\ B、\ C $インライン$ 、セット $インライン$ P、\ Q $インライン$ ;
- ゲームの初期状態 $インライン$(x_0、t_0)$インライン$ ;
また、最初のプレイヤーが多くのことを検出できると仮定されます $インライン$ n $インライン$ 時間内に $インライン$ \シータ> 0 $インライン$ その値は以下で定義されます。
最初のプレイヤーの戦略を定義する $ inline $ u(t)= U(x_0、t_0、v_t(\ cdot))$ inline $ 任意の測定可能な関数のセットで定義されたマップとして $ inline $ v(t)\ in Q、\ t \ ge t_0 $ inline $ 、および次のプロパティを所有しています:任意の測定可能 $ inline $ v(t)\ in Q、\ t \ ge t_0 $ inline $ 機能 $ inline $ u(t)= U(x_0、t_0、v_t(\ cdot))$ inline $ で測定可能 $インライン$ t $インライン$ そして $ inline $ u(t)\ in P $ inline $ 。
タスクA:初期状態を見つける $インライン$(x_0、t_0)$インライン$ 最初のプレイヤーは、任意の測定可能なものにゲームの終わりを提供するような戦略を持っている $ inline $ v \ in Q $ inline $ 最終的な瞬間よりも遅くはありません。 そのような条件 $インライン$(x_0、t_0)$インライン$ 問題Aの解決策と呼ばれます
B: 2番目のプレーヤーには、ゲームの進行状況に関する完全な情報があります。
2番目のプレイヤーの戦略を定義する $インライン$ v(t)= V(x_0、t_0、u_t(\ cdot))$ inline $ 任意の測定可能な関数のセットで定義されたマップとして $ inline $ u(t)\ in P、\ t \ ge t_0 $ inline $ 、および次のプロパティを所有しています:任意の測定可能 $ inline $ u(t)\ in P、\ t \ ge t_0 $ inline $ 機能 $インライン$ v(t)= V(x_0、t_0、u_t(\ cdot))$ inline $ で測定可能 $インライン$ t $インライン$ そして $ inline $ v(t)\ in Q $ inline $ 。
タスクB:初期状態を見つける $インライン$(x_0、t_0)$インライン$ 2番目のプレーヤーは、任意の測定可能なものにゲームの終了を提供するような戦略を持っています $ inline $ u \ in P $ inline $ 最終的な瞬間よりも遅くはありません。 そのような条件 $インライン$(x_0、t_0)$インライン$ 問題Bの解決策を呼び出します。
仮定する $インライン$ M = M ^ 1 + M ^ 2 $インライン$ どこで $インライン$ M ^ 1 $インライン$ -空間の線形部分空間 $インライン$ \ mathbb {R} ^ n $インライン$ 、 $インライン$ M ^ 2 $インライン$ -凸コンパクト、 $インライン$ M ^ 2 \サブセットL ^ 1、\ L ^ 1 \ oplus M ^ 1 = \ mathbb {R} ^ n $ inline $ 。 同様に $インライン$ N = N ^ 1 + N ^ 2 $インライン$ どこで $インライン$ N ^ 1 $インライン$ -空間の線形部分空間 $インライン$ \ mathbb {R} ^ n $インライン$ 、 $インライン$ N ^ 2 $インライン$ -凸コンパクト、 $インライン$ N ^ 2 \サブセットL ^ 1、\ L ^ 1 \ oplus N ^ 1 = \ mathbb {R} ^ n $ inline $ 。 同時に $インライン$ \ pi $インライン$ -直交設計のオペレーター $インライン$ \ mathbb {R} ^ n $インライン$ で $インライン$ L ^ 1 $インライン$ 、 $ inline $ \ pi \ in \ mathbb {R} ^ {\ nu \ times n} $ inline $ 。 これらの構造は、一般的なケース(および慣性オブジェクトがある場合)のゲームが微分方程式系の次元よりも小さな次元の空間でプレイされることを考慮するために必要です。
サブセクション4.1。 セットから最初のプレイヤーを回避する問題の解決可能性の十分条件 $インライン$ n $インライン$
タスクB-最初のプレーヤーを2番目のプレーヤーで追跡するタスクを検討し、この問題が解決するポイントのセットを構築します。 そのため、このタイプの問題に対して、ポントリャーギンは希望するセット-交互合計-を作成する方法を考え出しました- $インライン$ W(t)$インライン$ [3]、[5]。 したがって、交互の合計は凸コンパクトであるだけでなく、 $インライン$ v $インライン$ -安定(つまり、必要な2番目のプレイヤーの戦略を構築することができます)、また、小さなゲームのサドルポイントが存在することを保証します[6、p。56](つまり、ゲームは原則的に決定可能です)-つまり 一度に。
[6、p。69-定理17.1]から、これらの条件下では代替定理を使用できることがわかります。
開始位置について $インライン$(t_0、x_0)$インライン$ そして選択 $ inline $ \ bar T \ ge t_0 $ inline $ 次の2つのステートメントのいずれかが真です。
1)または戦略があります $インライン$ \バー{v} $インライン$ すべての動きに対して $インライン$ x(t)= x(t、t_0、x_0、\ bar {v})$インライン$ 会議を提供します $ inline $ \ {\ tau、x(\ tau)\} \ in N $ inline $ 終了時間 $インライン$ \ tau <\ bar {T} $インライン$ 。 つまり、2番目のプレーヤーの位置戦略のクラスでは、追跡問題(問題B)は解決可能です。
2)または、そうでなければ、戦略があります $ inline $ \ bar {u} $ inline $ すべての動きに対して $インライン$ x(t)= x(t、t_0、x_0、\ bar {u})$インライン$ 多数の回避を提供します $インライン$ \イプシロン$インライン$ -その時点までのセット$ N $の近傍 $インライン$ \バー{T} $インライン$ 。 つまり、最初のプレーヤーの位置戦略のクラスでは、回避問題(問題A)は解決可能です。
また、 $インライン$ v $インライン$ セットの安定性 $インライン$ W(T)$インライン$ [6、p。62-定理15.1]に基づいて、次の条件が得られます。
$$ display $$ \ forall t \ in [t_0、\ bar T]:x(t_0)\ notin W(t)$$ display $$
最初のプレイヤーを初期位置から回避する問題を解決するための十分な条件です $インライン$(t_0、x_0)$インライン$ から $インライン$ \イプシロン$インライン$ セットの近傍 $インライン$ n $インライン$ 時間が経つにつれて $インライン$ \バーT $インライン$ 。
最初のプレーヤーのリソースがセットで定義されている場合 $インライン$ P $インライン$ セットで定義された2番目のプレーヤーのリソースを超過する $インライン$ Q $インライン$ そして $インライン$ n $インライン$ 、そしてそのような時間があります $インライン$ \シータ$インライン$ あれ $インライン$ W(\シータ)= \ emptyset $インライン$ 。
瞬間の存在 $インライン$ t $インライン$ どの包含 $ inline $ x(t)\ in W(t)$ inline $ 、範囲からの時間に対する問題Bの可解性を提供します $インライン$ [t、t + \シータ] $インライン$ 。
つまり、戦略を構築できます $インライン$ u(x_0、t_0、x(t))$インライン$ 条件を満たす:
$$ display $$ \ forall \ tau \ in [t、t + \ Theta]:x(\ tau、u(x_0、t_0、x(\ tau)))\ notin W(\ tau)$$ display $ $
したがって、セットの回避を確保するために $インライン$ n $インライン$ 、現在の時点について上記の条件を確認する必要があります $インライン$ t $インライン$ 、およびその後のすべての瞬間の深さまで $インライン$ t + \シータ$インライン$ 。
多くの , :
, . - , ( ), , .
, , , : 5, 2, -- 1, 4. .
$インライン$ M $インライン$ . $インライン$ M $インライン$ :
4.2.
, 。 , , , :
( ) :
, 。
, , .
:
$インライン$ M $インライン$ :
" " ;
- , — :
, .
$インライン$ M $インライン$ 。
, , , , , , .
, , , .
, , , [6, . 69], :
どこで
15.2 [6, . 65], , , , .
$インライン$ M $インライン$ 。 - , , :
-- :
:
, , .. どこで 、 — . .. 、 - .
, $インライン$ M $インライン$ , , , .
— , , . , . 同時に
— , , .
—
, , . — " ", . .
:
ここに — $インライン$ x $インライン$ , — ,
,
.
.
.
.
, :
.
.
.
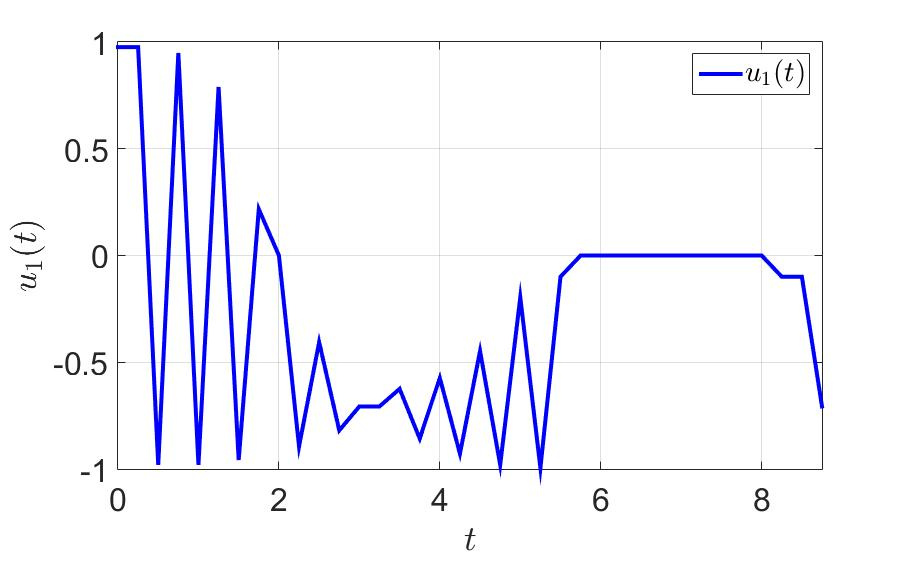
.
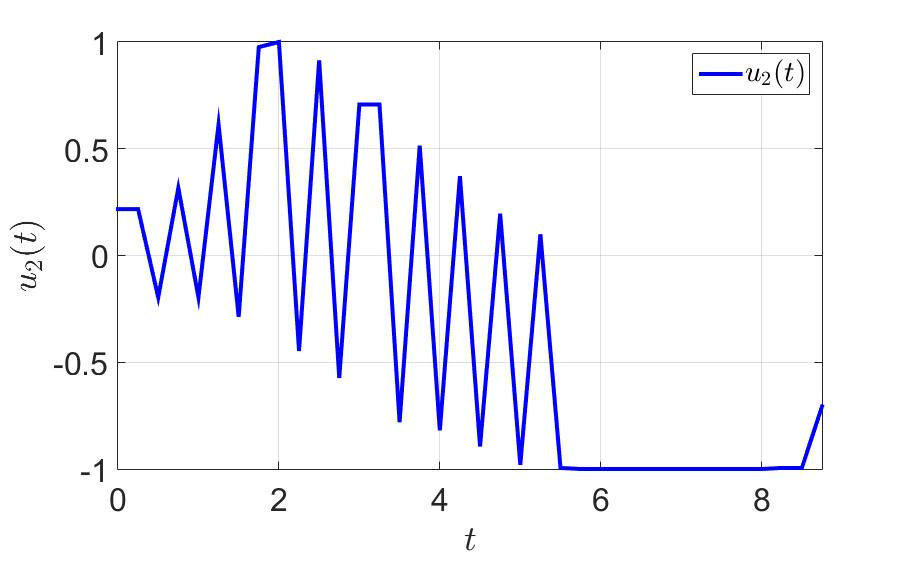
, , , .
結論
( , , ), — "" "" , (. .. c, .. .. ), .
: GitHub
, 19 , , C++ , , .. . .
, .. , , , .. " " .
.
UPD: technic93 , (. ).
[1] .. . . , , », , 1983
[2] .. : , , , 1968
[3] .. , , , 1990
[4] .. , .. , .. . , , 2007
[5] .., .., .. , , 2007
[6] .., .. , , , 1974
[7] .., . , , , 1972
[8] .., .., .., .. , , , 1969
( jul305a@gmail.com )