このシリーズの記事では、ビデオゲームの
逆運動学を紹介します。 旅を始める前に、
手続き型アニメーションを使用するいくつかのゲームと、それらが従来のリソースベースのアニメーションとどのように異なるかについてお話します。
シリーズは、次の部分で構成されます。
パート1.手続き型アニメーションの概要
ほとんどのゲームでは、キャラクターアニメーションは「静的」です。 キャラクターが画面上を移動すると、アーティストは特定の動きを作成します。 それらは手動で作成されるか、モーションキャプチャを使用して記録されます。 この場合のアニメーションは、事前に作成された
リソースです。 キャラクターが別のアクションを実行する必要がある場合、別のアニメーションが必要です。 キャラクターの動きを実装するこの方法は、ゲーム業界ではかなり標準的です。 歩行、ジャンプ、射撃などの最も一般的に使用される動作を含むアニメーションの大規模で詳細なコレクションがあります。 従来のアニメーションはゲーム業界を支配していますが、同等の代替手段があります。
手続き型アニメーションの概念を紹介したいと思います。
ここでの主なアイデアは、キャラクターの状態の瞬間を手続き的に生成できるということです。 手続き型アニメーションを生成するための最も標準的な手法の1つは、物理シミュレーションを使用します。 したがって、多くの場合、
物理アニメーション (
Wikipedia )と呼ばれます。 典型的な例は水です。 手動でアニメーション化するか、
流体力学を考慮したアニメーションを使用できます。
以下では、剛体シミュレーションを使用する物理アニメーションの非常に具体的な亜種について説明します。 同じタイプのシミュレーションは、UnityやUnrealなどのゲームエンジンで一般的に使用されています。 この単純な原理がゲームでどのように使用されて物理的なアニメーションを作成するかを見てみましょう。
ラグドール物理学
物理的なアニメーションの核となるのは、キャラクターの動きをシミュレートする可能性の原則です。 人体を支配するプロセスと制限を再作成することにより、現実的な行動の作成に近づくことができます。 手続き型アニメーションを作成する最も簡単で効果的な方法の1つは
、ラグドール(ラグドール、ラグドール)の
物理学を使用することです(
Wikipedia )。 アイデアは、ヒューマノイドボディを作成し、そのすべてのリンクをジョイントで接続して、実際のプロトタイプが示す自由度を再現することです。 固体物理と関節の制約を使用するだけで、人の体の転倒をシミュレートできます。 これは、「死のアニメーション」でお金を節約するだけではありません。 また、現実的に落ちて環境と相互作用するキャラクターを作成することもできます。 そのようなタスクは、精度に関係なく、既製のアニメーションセットだけでは解決することはほとんど不可能です。
ラグドールの最大の欠点は、その非常に予測不可能なことであり、これはしばしば非常に面白い動作につながります。
今日、ラグドールはゲームで非常によく知られています。 Unityには、人型モデルをラグドールにすばやく変換できるシンプルな
ラグドールウィザードツールがあります。
ソリッドステートシミュレーション
ラグドールの主な問題は、モーションコントロールの欠如です。 体の各部をジョイントで接続すると、キャラクターは歩くこともジャンプすることもできなくなります。 彼は落ちるだけです。 ただし、混合アプローチを使用できる状況があります。
Grow Homeが数学を使用してパーソナリティを生成する方法の記事で
、ゲームジャーナリストの
Alex WiltshireがUbisoftに
Grow Homeについて話しています。 このゲームの主な機能の1つは、主人公の動きの悪さ(BUD)です。 少なくとも
従来の意味では、ゲームには既製のアニメーションはありません。 プレーヤーが移動すると、脚と腕の位置はコードによって制御されます。 体の一部にはラグドールと同じ制限が適用されるため、魅力的なアニメーションを作成する必要があります。
同様の原則が
Rain Worldでも積極的に使用されています。 ゲーム内の各動物には、複数のコライダーで構成される体があります。 それらの一部はコードによって制御され、その他はアーティキュレーションによって制御されます。 これは以下のアニメーションで見ることができます。 猛禽類の翼の端点はプログラムで移動し、残りの骨はヒンジで接続されています。 エンドポイント管理は、そうでなければ不可能だったスムーズなアニメーションを自動的に作成します。
Grow HomeとRain Worldの両方で、手続き型アニメーションを使用してキャラクターのリアリズムを強化します。 ただし、コントローラーはこれらのアニメーションに依存しません。
Gang Beastsゲームでは
、この概念はさらに発展しています。 ゲームはラグドール物理学の使用に起因するぼやけた動きを完全に承認します。 その結果、予測不可能な動きのある面白いキャラクターができます。
逆運動学
剛体シミュレーションにより、アニメーションを簡単に作成できます。 バドの腕と脚がどこにあるべきかを示し、物理エンジンが残りを行います。 この非常にシンプルなアプローチはシンプルなキャラクターで機能しますが、多くの場合リアリズムに欠けています。 ソリッドボディシミュレーションでは、重力や質量などのパラメーターのみが考慮されますが、コンテキストに関する知識はありません。 多くの場合、重力や化合物による制限の影響下でのみ作用するものを作成する必要があります。
手続き型アニメーションを作成する次のステップは、
逆運動学として知られています。 あらゆるタイプのラグドールについて、インバースキネマティクスは、目的の目標を達成するためにそれを動かす方法を計算します。 Grow HomeとRain Worldでは、物理学自体が重力の影響を受ける化合物の移動方法を決定します。 逆運動学は、それらを適切なフェーズで移動させます。
このコンセプトが積極的に使用された最初のインディーズゲームの1つは、
The Future Proof Gamesスタジオの The Majesty Of Colorでした。 その中で、プレイヤーは海の生き物の触手を制御します。 Rain Worldの鳥の羽とは異なり、この触手はヒンジだけではありません。 触手の端点が目的の点に到達するように、各セグメントが回転します。 このアニメーションでソリッドボディシミュレーションのみを使用した場合、触手はロープのようにこのポイントに「固定」されているように見えます。
逆運動学は、多くの問題を解決するために使用できます。 最も標準的なのは、特定のオブジェクトへのヒューマノイドキャラクターの自然な動きです。 開発者は、事前定義されたアニメーションを使用する代わりに、手が達成すべき目標を単に示すだけです。 逆運動学は残りを行い、手の関節を動かす最も自然な方法を見つけます。 ソリッドのシミュレーションのみを使用すると、動きがぎくしゃくし、体の一部が単にドラッグアンドドロップされているように見えます。
MechanimというUnityアニメーションエディターには、開発者がヒューマノイドキャラクターに逆運動学を使用できるツール(
Unityヘルプ )があります。

この一連の記事の残りでは、逆運動学の問題の解決に焦点を当てます。 ロボットアームまたはモンスターの触手を制御する方法を理解します。
パート2.直接運動学の数学
さあ、
逆運動学の世界への旅を始めましょう。 この問題を解決する方法はたくさんありますが、それらはすべて
直接運動学から始まります。
インバースキネマティクスは、空間内のポイントを取得し、それに到達するために手を動かす方法を教えてくれます。 直接運動学は、反対の
二重問題を解決します。 私たちがどのように手を動かすかを知って、彼女は手が空間のどの点に達するかを教えてくれます。
ロボットアーム
逆運動学はもともと
ロボットマニピュレーターを制御するために使用されました。 したがって、このシリーズの記事では、ロボット工学の前提と用語を使用します。 ただし、これは逆運動学の可能なアプリケーションを制限しません。 人間の手、クモの足、触手に使用できます。
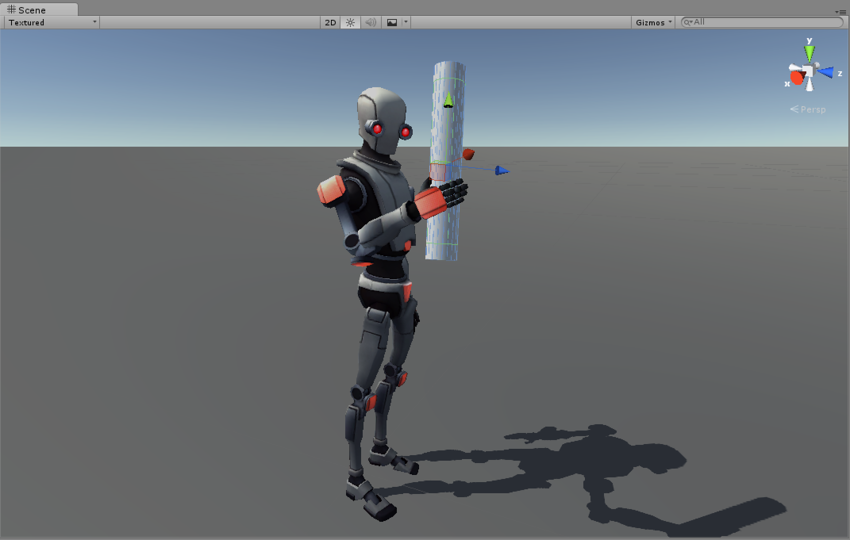
まず、「ロボットアーム」という用語の意味を示すことから始めましょう。

上の画像は、「ジョイント」で接続された「手足」で作られた標準的なロボットアームを示しています。 画像に示されているロボットには5つの独立した関節があるため、5つ
の自由度があると考えられています。 各ジョイントはエンジンによって制御されます。これにより、ジョイントに取り付けられたリンクを特定の角度に移動できます。
より一般的な例を検討するために、共同図を描くことができます。 この記事では、各ジョイントが1つの軸でのみ回転できると仮定します。
ロボットアームの端に取り付けられたツールは、
エンドリンクと呼ばれます。 コンテキストに応じて、1自由度と見なされる場合とされない場合があります。 この記事では、目的のポイントに到達するための移動のみに焦点を当てるため、最終リンクは考慮されません。
直接運動学
この例では、各ジョイントは1つの軸で回転できます。 したがって、各関節の状態は角度として測定されます。 各ジョイントを特定の角度で回転させることにより、最終的なリンクが空間の異なるポイントに到達できるようにします。 エンドリンクが既知のジョイント角度にある場所を特定することは、
直接運動学と呼ばれます。
直接運動学は「単純な」問題です。 これは、角度の各セットに対して、不確実性なしに計算できる単一の結果があることを意味します。 送信するデータに応じてロボットアームがどのように動くかを判断することは、逆運動学の逆問題を見つけるために必要なステップです。
幾何学的解釈
コードの記述を開始する前に、直接運動学の背後にある数学的構造を理解する必要があります。 しかし、まず第一に、それが空間的および幾何学的に意味することを理解する必要があります。
3Dでターンを視覚化するのはそれほど簡単ではないので、2次元空間の単純なマニピュレーターから始めましょう。 ロボットアームには「開始位置」があります。これは、すべての関節が「ゼロ角」まで回転する構成です。
上の図は、3つの自由度を持つマニピュレーターを示しています。 各関節は、そのゼロ角度の位置まで回転します。つまり、ロボットは元の位置にあります。 ジョイントが回転すると、この構成がどのように変化するかを確認できます。

に
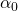
度。 これは、関節とリンクのチェーン全体の対応する動きにつながります

。
他のジョイントに取り付けられたモーターはまだ移動していないことに注意することが重要です。 各ジョイントは、結合の直接チェーンのローカル回転に寄与します。 次の図は、2番目のジョイントが回転したときの構成の変更を示しています
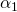
度。
役職
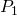
定義のみ
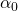
でも

すでに影響し、
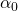
、そして
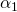
。 回転座標系(赤と青の矢印)は、接続されている以前の接続チェーンの回転の合計に従って方向付けられます。
数学
前のスキームから、直接運動学の問題を解決するには、埋め込まれた(従属)オブジェクトが回転するときの位置を計算する必要があることは明らかです。
2つのジョイントの例を使用して計算する方法を見てみましょう。 2つの要素の解決策を見つけたら、このプロセスを繰り返して任意の長さのチェーンを解決できます。
最初のジョイントが初期位置にある単純なケースから始めましょう。 つまり、
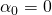
以下の図のように:
これは次のことを意味します。
いつ
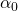
ゼロに等しくない、我々はちょうど支点で距離ベクトルを回転させる必要があります
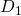
周り

に
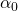
度:
数学的には、これは次のように書くことができます。
以下では、三角法に
AngleAxisことなく
AngleAxis関数(
Unityドキュメント )を使用する方法を学びます。
同じ論理を再現すると、次の方程式を得ることができます

:
そして最後に、一般的な方程式:
この記事の次のパートでは、この式をC#コードで実装するのがどのように
便利かを説明します。
Denavit-Hartenberg行列はどうですか?エンジニアリングの知識がある場合は、この問題を別の方法で解決できます。 直接および逆運動学の問題は広く知られており、それらを解決するための標準化されたアプローチがいくつか存在します。 それらの1つは
、Denavit-Hartenberg (
ウィキペディア )のパラメーターと呼ばれる4つのパラメーターの各ジョイントへのバインドです。 それらをマトリックス形式で操作すると便利であり、逆運動学の問題の分析ソリューションに最適です。
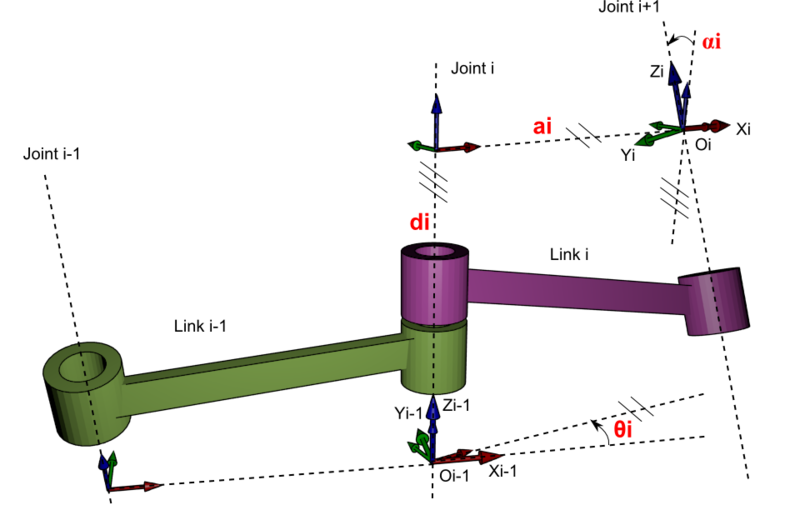
ただし、この記事ではそれらを使用しません。 Denavit-Hartenberg行列を解くには、多くのプログラマが理解するよりも多くの数学が必要です。 私が選択したアプローチでは、より一般的な最適化アルゴリズムである
勾配降下法を使用しています。
パート3.直接運動学の実現
このパートでは、
直接運動学の問題を解決し続けます。 最後の部分で数学的解決策を見つけたので、UnityのC#コードでそれを実装する方法を学びます。 次の「勾配降下法の紹介」では、最終的に
逆運動学の問題を解決するための理論的根拠を示します。
はじめに
前のパートでは、ロボットアームの動きを形式化しました。 3つのジョイントの簡単な例から始めました。 初期位置では、以下に示す構成になっています。
異なる

図中のデカルト座標、または
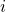
2番目のジョイント。 開始位置に対する回転を決定する
ローカル角度は、
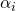
。
ジョイントを回すとき、次の図を観察します。
このシステムの動作は、次のステートメントで要約できます。
- ターン 。 グローバルターン
 ジョイントは、以前のすべてのジョイントの回転の合計です。
ジョイントは、以前のすべてのジョイントの回転の合計です。
- 位置 グローバルポジション
 ジョイントは次のように定義されます:
ジョイントは次のように定義されます:
上記のすべてを考慮すると、Unityでこれらの動作を実装する可能な方法を考え出すことができます。
ゲームオブジェクト階層
Unityはすでに、上記のすべての要件を実装する方法を持っています:
ペアレンティングシステム 。 ゲームオブジェクトを別のオブジェクトの子にすると、そのオブジェクトの位置、回転、スケールが自動的に継承されます。
索具に慣れている場合、これは驚くことではありません。 ヒューマノイドキャラクターの関節である骨には、ターンと動きが継承される親システムもあります。 Michael Erbetnotに
よるUnity Animation 3:Character Setupの画像は、この明白な例を示しています。
接続階層を作成する場合、すべてのローカルオイラー角がゼロに等しい場合、ロボットアームが元の位置にあることを確認する必要があります。 ヒューマノイドキャラクターの場合、これは通常、上の画像に示されている
標準のT字型のポーズです。
実装
Unityで子コンポーネントを作成する機能により、直接運動学の問題が
事実上解決されます。 残念ながら、これでは十分ではありません。 一連の記事の次の部分では、ロボットアーム
を動かさ
ずに最終的なリンクの位置を確認する方法が実際に必要であることがわかります。 これにより、この基本的なUnity機能を独自の方法で実装する必要があります。
最初のステップは、ロボットアームの各関節に関する情報を保存することです。 これは、次の例の
RobotJointなどのスクリプトを使用して実現できます。
using UnityEngine; public class RobotJoint : MonoBehaviour { public Vector3 Axis; public Vector3 StartOffset; void Awake () { StartOffset = transform.localPosition; } }
計算を簡素化するために、各ジョイントはローカル軸の1つ(X、Y、またはZ)でのみ回転できると想定しています。これを変数
Axisで表し、回転軸に対する座標の値を
1します。 ジョイントがY軸に沿って回転する場合、軸の形式は
(0,1,0)ます。 これにより、
IFを使用してコンストラクトを削除できることがわかります。
ForwardKinematics関数を作成しましょう。 彼女は
float型の
angles配列を取得します。 名前はそれ自身を表しています
angles[i]には、i番目のジョイントのローカル回転値が含まれます。 この関数は、グローバルリンクの最終リンクの位置を返します。
public Vector3 ForwardKinematics (float [] angles) { ... }
このコードは、上記の位置方程式の単純なC#実装です。
rotate関数は、便利な
Quaternion.AngleAxis関数を通じて実装されます。
Vector3 prevPoint = Joints[0].transform.position; Quaternion rotation = Quaternion.identity; for (int i = 1; i < Joints.Length; i++) {
クォータニオンのサポートが必要ですか?ユニティのターンは、多くの場合、オイラー角で記述されます。 これらは、X、Y、Z軸に沿ったオブジェクトの回転に対応する3つの数値であり、オイラー角は、空間内
のオブジェクトの
ロール 、
ピッチ 、
ヨーを表します。 ただし、数学的な観点からは、オイラー角を使用すると、かなり不快な問題が発生する可能性があります。
四元数の助けを借りてコーナーで作業する方が便利です。 四元数は、
ターンを記述するために使用できる数学的なオブジェクトです。 対照的に、オイラー角は
方向を表します。 クォータニオンは、ある方向から別の方向に進むパスを表します。 技術的な観点から見ると、これは非常に単純化されていますが、私たちの記事にとっては十分すぎるほどです。
ローテーション⇔クォータニオン
四元数はターンとして表すことができます。 空間内のオブジェクトの回転は、数学的な観点から、その位置に四元数を掛けたものに類似しています。
Quaternion.AngleAxis関数を使用して、Unityの固定点を中心に回転を作成できます。 String
Quaternion.AngleAxis(angle, axis); 軸
axis周りの回転を
angle表すクォータニオンを作成します。 このコンテキストでは、
Axis値は
(1,0,0) 、
(0,1,0)または
(0,0,1)になり、それぞれX、YまたはZを意味します。
RobotJointクラスの
Axis 。
スピンの追加⇔四元数の乗算
2つのクォータニオンを乗算すると、両方のターンを含む新しいクォータニオンが作成されます。
forループの各反復で、
rotation変数に現在のクォータニオンが乗算されます。 これは、すべてのジョイントのすべての回転が含まれることを意味します。
四元数*ベクトル=回転ベクトル
最後に、この行で四元数が使用されます。
Vector3 nextPoint = prevPoint + rotation * Joints[i].StartOffset;
次のエントリと完全に一致しています。
クォータニオンとベクトルの積は回転を適用します。
[続きます。 2番目の記事では、逆運動学に注目します。]