PyTorchは、Facebookの管理下で開発されている最新の深層学習ライブラリです。 Caffe、Theano、TensorFlowなどの他の一般的なライブラリとは異なります。 これにより、研究者は最もワイルドなファンタジーを実現でき、エンジニアはこれらのファンタジーを簡単に実装できます。

この記事はPyTorchの簡潔な紹介であり、ライブラリにすばやく慣れ、その主要な機能と他のディープラーニングライブラリの中での位置を理解することを目的としています。

PyTorchは、Python言語のTorch7フレームワークに類似しています。 その開発は、Torch7の登場からわずか1年後の2012年にFacebookの腸から始まりましたが、PyTorchは一般公開され、2017年にのみ一般に公開されました。 この時点から、フレームワークは非常に急速に人気を博し、ますます多くの研究者の注目を集めています。 何がそんなに人気があるの？

残りのフレームワークの中に配置する

まず、ディープラーニングフレームワークとは何かを理解しましょう。 ディープラーニングは通常、多くの非線形変換の構成である関数の学習を意味すると理解されています。 このような複雑な関数は、フローまたは計算グラフとも呼ばれます。 ディープラーニングフレームワークでは、次の3つのことしかできません。

1. 計算のグラフを定義します。
2. 計算のグラフを区別します。
3. それを計算します。

関数の計算方法を早く知って、それを定義する柔軟性が高いほど良い。 すべてのフレームワークがビデオカードの全機能を使用できるようになったため、最初の基準は重要な役割を果たしなくなりました。 本当に興味があるのは、コンピューティングのフローを定義するための利用可能なオプションです。 ここでのすべてのフレームワークは、3つの大きなカテゴリに分類できます。

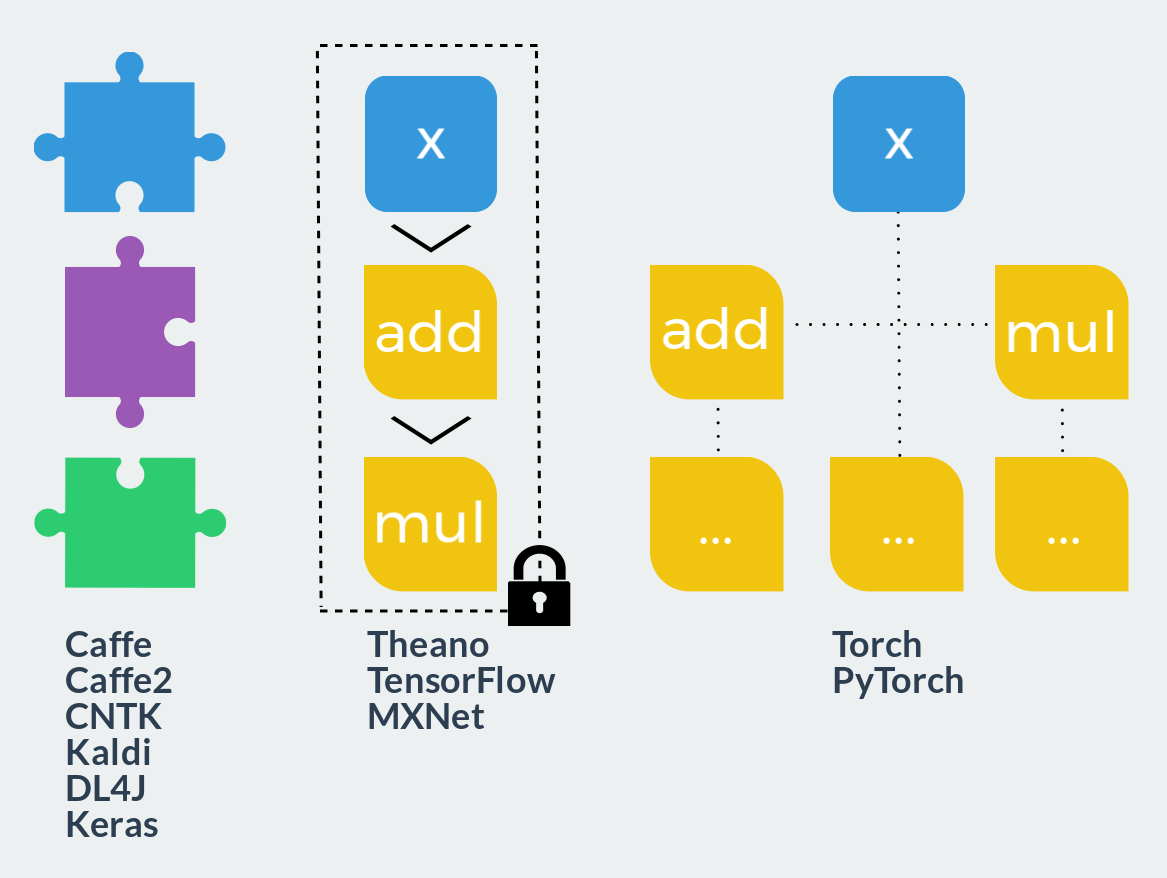
• 固定モジュール このアプローチは、レゴコンストラクターと比較できます。ユーザーは、定義済みのブロックを計算グラフに結合して起動します。 このような各ブロックには、前後の通路がすでに縫い付けられています。 新しいブロックを定義することは、既製のブロックを使用するよりもはるかに難しく、完全に異なる知識とスキルが必要です。 拡張性はほぼゼロですが、そのようなフレームワークにアイデアが完全に実装されている場合、開発速度は最大になります。 高度に最適化された事前に記述されたコードのおかげで、作業の速度も問題ありません。 典型的な代表者：Caffe、Caffe2、CNTK、Kaldi、DL4J、Keras（インターフェースとして）。
• 計算の静的グラフ。 これらのフレームワークは、ポリマークレイとすでに比較できます。説明の段階では、任意のサイズと複雑さの計算グラフを作成できますが、ベーキング（コンパイル）後は固体でモノリシックになります。 使用可能なアクションは2つだけです。グラフを順方向または逆方向に起動します。 このようなフレームワークはすべて、宣言型プログラミングスタイルを使用し、関数型言語または数学表記に似ています。 一方では、このアプローチは、設計段階での柔軟性と実行時の速度を兼ね備えています。 一方、関数型言語の場合と同様に、デバッグは真の頭痛の種になり、パラダイムを超えたモデルを実装するには、巨人の努力または大きな松葉杖が必要です。 代表者：Theano、TensorFlow、MXNet。
• 計算の動的グラフ。 各実行の前に静的グラフを再構築できると想像してください。 これは、このクラスのフレームワークでほぼ発生することです。 別のエンティティとしてのグラフのみがここにはありません。 命令型プログラミング言語のように、明示的な構築には複雑すぎて、実行時にのみ存在します。 より正確には、グラフは毎回直接パスを使用して動的に作成され、逆パスを作成できます。 このアプローチは、最大限の柔軟性と拡張性を提供し、計算で使用されるプログラミング言語のすべての機能を使用できるようにし、ユーザーを何にも制限しません。 このクラスのフレームワークには、TorchとPyTorchが含まれます。

私たちの多くは、NumPyのみを使用して、ディープラーニングに対処し始めたと確信しています。 その上に直接文章を書くのは簡単で、重みを更新するための式は紙の上で計算することも、アストラルから既製の重みを取得することもできます。 このような最初のコードは次のようになります。

import numpy as np def MyNetworkForward(weights, bias, x): h1 = weights @ x + bias a1 = np.tanh(h1) return a1 y = MyNetworkForward(weights, bias, x) loss = np.mean((y - y_hat) ** 2) 

時間が経つにつれて、ネットワークアーキテクチャはより複雑で深くなり、NumPy、鉛筆、紙の機能はもはや十分ではありません。 この時点でアストラルとの接続がまだ閉じられておらず、体重を得る場所がある場合は、運がいいです。 そうでなければ、思わず2つのことを考え始めます：

1. これで、ビデオカードで計算を実行できます。
2. すべての勾配がカウントされることを望みます。

同時に、私は通常のアプローチを変更したくありません、ただ書きたいです：

 import numpy as np def MyNetworkForward(weights, bias, x): h1 = weights @ x + bias a1 = np.tanh(h1) return a1 weights.cuda() bias.cuda() x.cuda() y = MyNetworkForward(weights, bias, x) loss = np.mean((y - y_hat) ** 2) loss.magically_calculate_backward_pass() 

さて、何だと思う？ PyTorchはまさにそれを行います！ 完全に正しいコードは次のとおりです。

 import torch def MyNetworkForward(weights, bias, x): h1 = weights @ x + bias a1 = torch.tanh(h1) return a1 weights = weights.cuda() bias = bias.cuda() x = x.cuda() y = MyNetworkForward(weights, bias, x) loss = torch.mean((y - y_hat) ** 2) loss.backward() 

既に計算されたパラメーターの更新を適用するためにのみ残ります。

TheanoおよびTensorFlowでは、宣言型DSLのグラフについて説明します。このグラフは、内部バイトコードにコンパイルされ、C ++で記述されたモノリシックカーネルで実行されるか、Cコードにコンパイルされて別のバイナリオブジェクトとして実行されます。 コンパイルの時点でグラフ全体を把握している場合、たとえば記号的に簡単に区別できます。 ただし、コンパイル段階は必要ですか？

わかった、いや。 計算と同時にグラフを動的に作成することを妨げるものは何もありません！ また、自動微分（AD）技術のおかげで、いつでもどの状態でもグラフを取得して微分できます。 グラフをコンパイルする必要はまったくありません。 速度の面では、Pythonインタープリターから軽量のネイティブプロシージャを呼び出すことは、コンパイルされたコードを実行するより遅くありません。

DSLとコンパイルに限らず、Pythonのすべての機能を使用して、コードを本当に動的にすることができます。 たとえば、偶数日と奇数日にさまざまなアクティベーション機能を適用します。

 from datetime import date import torch.nn.functional as F ... if date.today().day % 2 == 0: x = F.relu(x) else: x = F.linear(x) ... 

または、ユーザーが入力したばかりの値をテンソルに追加するレイヤーを作成できます。

 ... x += int(input()) ... 

記事の最後に、より有用な例を示します。 要約すると、上記のすべては次の式で表すことができます。
PyTorch = NumPy + CUDA + AD 。

テンソル計算

NumPyの部分から始めましょう。 Tensorコンピューティングは、PyTorchの基盤です。PyTorchは、他のすべての機能が構築されるフレームワークです。 残念ながら、この側面におけるライブラリの力と表現力がNumPyの力と表現力と一致するとは言えません。 テンソルを使用する場合、PyTorchは最大限のシンプルさと透明性の原則に導かれ、BLAS呼び出しの微妙なラッパーを提供します。

テンソル

テンソルによって保存されるデータのタイプは、そのコンストラクターの名前に反映されます。 パラメーターのないコンストラクターは特別な値を返します。次元のないテンソルは、どの操作にも使用できません。

 >>> torch.FloatTensor() [torch.FloatTensor with no dimension] 

可能なすべてのタイプ：

 torch.HalfTensor # 16 ,    torch.FloatTensor # 32 ,    torch.DoubleTensor # 64 ,    torch.ShortTensor # 16 , ,  torch.IntTensor # 32 , ,  torch.LongTensor # 64 , ,  torch.CharTensor # 8 , ,  torch.ByteTensor # 8 , ,  

デフォルトまたはタイプの自動検出はありません。 torch.Tensorはtorch.FloatTensorです。

NumPyのような自動キャストも実行されません。

 >>> a = torch.FloatTensor([1.0]) >>> b = torch.DoubleTensor([2.0]) >>> a * b 

 TypeError: mul received an invalid combination of arguments - got (torch.DoubleTensor), but expected one of: * (float value) didn't match because some of the arguments have invalid types: (torch.DoubleTensor) * (torch.FloatTensor other) didn't match because some of the arguments have invalid types: (torch.DoubleTensor) 

この点で、 PyTorchより厳格で安全です。メモリ消費量が2倍に増えても、 PyTorchないので、定数のタイプが混乱します。 明示的な型変換は、適切な名前のメソッドを使用して利用できます。

 >>> a = torch.IntTensor([1]) >>> a.byte() 1 [torch.ByteTensor of size 1] >>> a.float() 1 [torch.FloatTensor of size 1] 

x.type_as(y)は、 yと同じ型のxから値のテンソルを返します。

テンソルをそれ自体のタイプに縮小しても、コピーされません。

リストをパラメーターとしてテンソルコンストラクターに渡すと、対応する次元と対応するデータのテンソルが構築されます。

 >>> a = torch.IntTensor([[1, 2], [3, 4]]) >>> a 1 2 3 4 [torch.IntTensor of size 2x2] 

NumPyの場合と同様に、誤った形式のリストは許可されません。

 >>> torch.IntTensor([[1, 2], [3]]) 

 RuntimeError: inconsistent sequence length at index (1, 1) - expected 2 but got 1 

任意のタイプのシーケンスの値からテンソルを構築することができます 。これは非常に直感的で、NumPyの動作に対応します。

テンソルコンストラクターの別の可能な引数のセットは、そのサイズです。 引数の数によって次元が決まります。

このメソッドによって構築されたテンソルには、ガベージ-ランダムな値が含まれています。

 >>> torch.FloatTensor(1) 1.00000e-17 * -7.5072 [torch.FloatTensor of size 1] 

 >>> torch.FloatTensor(3, 3) -7.5072e-17 4.5909e-41 -7.5072e-17 4.5909e-41 -5.1601e+16 3.0712e-41 0.0000e+00 4.5909e-41 6.7262e-44 [torch.FloatTensor of size 3x3] 

索引付け

標準のPythonインデックス作成がサポートされています：インデックスの反転とスライス。

 >>> a = torch.IntTensor([[1, 2, 3], [4, 5, 6]]) >>> a 1 2 3 4 5 6 [torch.IntTensor of size 2x3] 

 >>> a[0] 1 2 3 [torch.IntTensor of size 3] 

 >>> a[0][1] 2 >>> a[0, 1] 2 

 >>> a[:, 0] 1 4 [torch.IntTensor of size 2] >>> a[0, 1:3] 2 3 [torch.IntTensor of size 2] 

他のテンソルもインデックスにすることができます。 ただし、2つの可能性しかありません。

• ゼロ次元（ベクトルの場合は要素、行列の場合は行）による1次元のtorch.LongTensorインデックス。
• マスクとして機能する0または1のみを含む、対応するtorch.ByteTensor 。

 >>> a = torch.ByteTensor(3,4).random_() >>> a 26 119 225 238 83 123 182 83 136 5 96 68 [torch.ByteTensor of size 3x4] >>> a[torch.LongTensor([0, 2])] 81 218 40 131 144 46 196 6 [torch.ByteTensor of size 2x4] 

 >>> a > 128 0 1 0 1 0 0 1 0 1 0 1 0 [torch.ByteTensor of size 3x4] >>> a[a > 128] 218 131 253 144 196 [torch.ByteTensor of size 5] 

x.dim() 、 x.size()およびx.type()関数は、テンソルに関するすべての情報を見つけるのに役立ち、 x.data_ptr()は、データが存在するメモリ内の場所を示します。

 >>> a = torch.Tensor(3, 3) >>> a.dim() 2 >>> a.size() torch.Size([3, 3]) >>> a.type() 'torch.FloatTensor' >>> a.data_ptr() 94124953185440 

テンソル操作

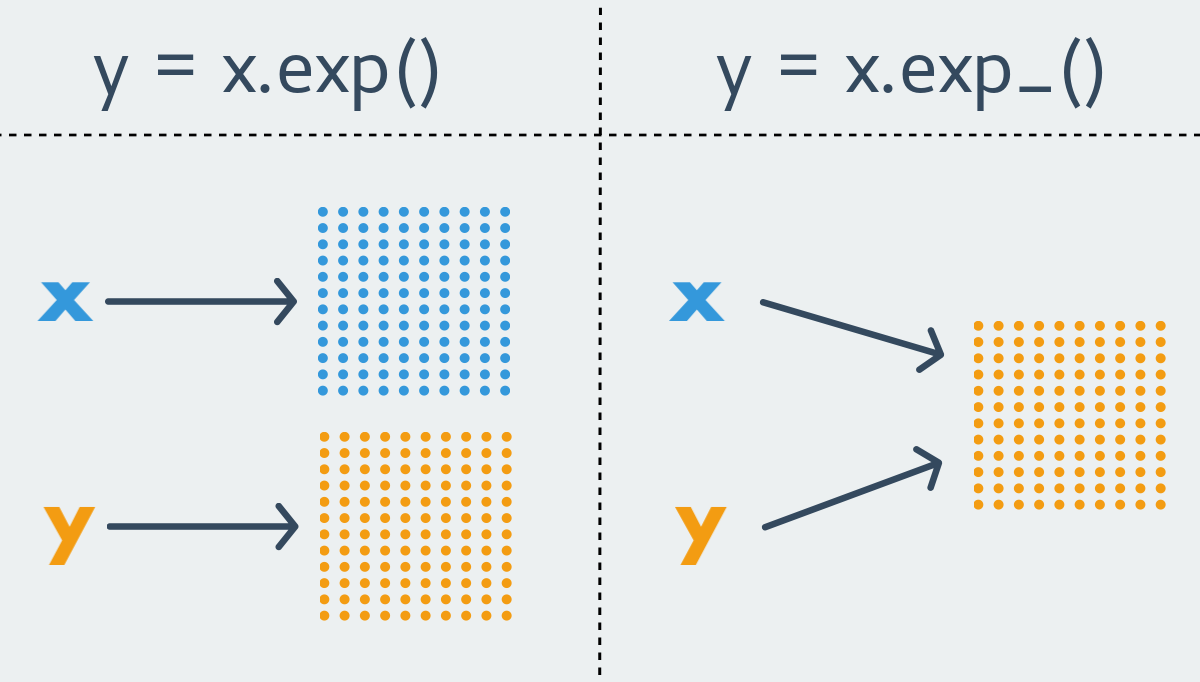
PyTorchの命名規則では、 xxx形式の関数は新しいテンソルを返します。 不変の関数です。 対照的に、形式xxx_の関数は、初期テンソルを変更します。 変更可能な関数です。 後者はインプレース関数とも呼ばれます。

PyTorchのほとんどすべての不変の関数には、それほど純粋ではない関数が存在します。 ただし、関数は1つのバリアントにのみ存在することもあります。 明らかな理由により、テンソルのサイズ変更関数は常に不変です。

テンソルで利用可能なすべての操作をリストするのではなく、最も重要なものだけを取り上げ、それらをカテゴリに分類します。

初期化関数

原則として、特定のサイズの新しいテンソルを作成するときの初期化に使用されます

 x = torch.FloatTensor(3, 4) #  x.zero_() #  

可変関数はオブジェクトへの参照を返すため、宣言と初期化を1行で記述する方が便利です。

 x = torch.FloatTensor(3, 4).zero_() 

• x.zero_()
  テンソルをゼロで初期化します。 不変のオプションはありません。
• x.fill_(n)
  テンソルを定数nで埋めます。 同様に、不変のオプションはありません。
• x.random_(from, to)
  テンソルを離散 （実数値テンソルでも）均一分布からのサンプルで満たします。
  

  fromとto指定さtoいない場合from使用されるデータ型の下限と上限にそれぞれ等しくなります。
  

• x.uniform_(from=0, to=1)
  また、均一な分布ですが、すでに連続しており、より馴染みのあるデフォルトの境界線があります。 実数値のテンソルでのみ利用可能です。
• x.normal_(mean=0, std=1)
  正規分布。 実数値のテンソルでのみ利用可能です。
• x.bernoulli_(p=0.5)
  ベルヌーイ分布。 pとして、値0 <= p <= 1の同じ次元のスカラーまたはテンソルを使用できます。 このバージョンは、セマンティクスが異なるため、不変のオプションと区別することが重要です。 呼び出しy = x.bernoulli() y.bernoulli_(x) y = x.bernoulli()同等です。 ここのxは、分布パラメータのテンソルとして使用されます。
• torch.eye(n, m)
nxm単位行列を作成します。 ここでは、私には不明な理由で、インプレースオプションはもう存在しません。

指数分布および幾何分布、コーシー分布、正規分布の対数、およびテンソルを初期化するためのいくつかのより複雑なオプションも利用できます。 ドキュメントをご覧ください。

数学演算

最も頻繁に使用されるグループ。 ここでの操作がテンソルのサイズとタイプを変更しない場合、インプレースオプションがあります。

• z = x.add(y)
z = torch.add(x, y)
x.add_(y)
  追加。
• z = x.sub(y)
z = torch.sub(x, y)
x.sub_(y)
  減算
• z = x.mul(y)
z = torch.mul(x, y)
x.mul_(y)
  乗算
• z = x.div(y)
z = torch.div(x, y)
x.div_(y)
  部門。 整数型の場合、除算は整数です。
• z = x.exp()
z = torch.exp(x)
x.exp_()
  出展者。
• z = x.log()
z = torch.log(x)
x.log_()
  自然対数。
• z = x.log1p()
z = torch.log1p(x)
x.log1p_()
x + 1の自然対数。 この関数は、小さなxの計算の精度に対して最適化されています。
• z = x.abs()
z = torch.abs(x)
x.abs_()
  モジュール

当然のことながら、すべての基本的な三角関数演算は、それらが期待される形で存在します。 ここで、ささいな関数に目を向けます。

• z = xt()
z = torch.t(x)
x.t_()
  転置。 テンソルのサイズが変化するという事実にもかかわらず、メモリ内のデータのサイズは同じままなので、関数のインプレースバージョンがあります。
• z = x.mm(y)
z = torch.mm(x, y)
  行列の乗算。
• z = x.mv(v)
z = torch.mv(x, v)
  行列とベクトルの乗算。
• z = x.dot(y)
z = torch.dot(x, y)
  テンソルのスカラー乗算。
• bz = bx.bmm(by)
bz = torch.bmm(bx, by)
  マトリックスとバッチ全体を乗算します。
  

   >>> bx = torch.randn(10, 3, 4) >>> by = torch.randn(10, 4, 5) >>> bz = bx.bmm(bz) >>> bz.size() torch.Size([10, 3, 5]) 

addbmm 、 addmm 、 addmv 、 addr 、 baddbmm 、 btrifact 、 btrisolve 、 eig 、 btrisolveなど、複雑なシグネチャを持つBLAS関数の完全な類似物もあります。

削減操作は、署名が互いに似ています。 それらのほとんどすべてが、最後のオプション引数とともに、 dim縮小が実行される次元を受け入れます。 引数が指定されていない場合、演算はテンソル全体に作用します。

• s = x.mean(dim)
s = torch.mean(x, dim)
  サンプル平均。 実数値のテンソルに対してのみ定義されます。
• s = x.std(dim)
s = torch.std(x, dim)
  選択的な標準偏差。 実数値のテンソルに対してのみ定義されます。
• s = x.var(dim)
s = torch.var(x, dim)
  選択的分散。 実数値のテンソルに対してのみ定義されます。
• s = x.median(dim)
s = torch.median(x, dim)
  中央値
• s = x.sum(dim)
s = torch.sum(x, dim)
  量。
• s = x.prod(dim)
s = torch.prod(x, dim)
  仕事。
• s = x.max(dim)
s = torch.max(x, dim)
  最大。
• s = x.min(dim)
s = torch.min(x, dim)
  最低限。

すべての種類の比較演算（ eq 、 ne 、 gt 、 lt 、 ge 、 le ）も定義されており、作業の結果としてByteTensorマスクを返します。

+ 、 += 、 - 、 -= 、 * 、 *= 、 / 、 /= 、 @演算子は、上記の対応する関数を呼び出すことで、期待どおりに機能します。 ただし、APIの複雑さと不完全な自明性のため、演算子の使用はお勧めしませんが、代わりに必要な関数の明示的な呼び出しを使用します。 少なくとも2つのスタイルを混在させないでください。これにより、 x += x.mul_(2)ようなエラーを回避できます。

PyTorchには、ソートや関数の要素ごとの適用など、多くの興味深い関数がまだストックされていますが、それらのすべてがディープラーニングで使用されることはほとんどありません。 PyTorchをテンソル計算のライブラリとして使用する場合は、これを行う前にドキュメントを参照することを忘れないでください。

放送放送

放送は複雑なトピックです。 私の意見では、そうでなければ良いと思います。 しかし、彼は最新のリリースの1つにしか登場しませんでした。 PyTorchの多くの操作は、今では使い慣れたNumPyスタイルでのブロードキャストをサポートしています。

一般的に、2つの空でないテンソルは、最後の測定から開始して、この次元の両方のテンソルのサイズが等しいか、どちらか一方のサイズが1に等しいか、テンソルの測定値がもはや存在しない場合、 ブロードキャスト可能と呼ばれます。 例で理解しやすくなりました。

 >>> x = torch.FloatTensor(5, 7, 3) >>> y = torch.FloatTensor(5, 7, 3) # broadcastable,  :  ,    ,  

 >>> x = torch.FloatTensor(5, 3, 4, 1) >>> y = torch.FloatTensor( 3, 1, 1) # broadcastable,     ,         ,     ,        

 >>> x = torch.FloatTensor(5, 2, 4, 1) >>> y = torch.FloatTensor( 3, 1, 1) #  broadcastable,       (2 != 3)            

 >>> x = torch.FloatTensor() >>> y = torch.FloatTensor(2, 2) #  broadcastable,  x     ()  

次元テンソルtorch.Size([1])はスカラーであり、明らかに他のテンソルでブロードキャスト可能です。

ブロードキャストから生じるテンソルのサイズは、次のように計算されます。

1. テンソルの測定数が等しくない場合、必要に応じて単位が追加されます。
2. 次に、結果のテンソルのサイズが初期テンソルの要素ごとの最大値として計算されます。

 >>> x = torch.FloatTensor(5, 1, 4, 1) >>> y = torch.FloatTensor( 3, 1, 1) >>> (x+y).size() torch.Size([5, 3, 4, 1]) 

この例では、2番目のテンソルの次元に最初に単位が追加され、その後、要素ごとの最大値が結果のテンソルの次元を決定しました。

キャッチはインプレース操作です。 初期テンソルのサイズが変わらない場合にのみ、ブロードキャストが許可されます。

 >>> x = torch.FloatTensor(5, 3, 4, 1) >>> y = torch.FloatTensor( 3, 1, 1) >>> (x.add_(y)).size() torch.Size([5, 3, 4, 1]) 

 >>> x=torch.FloatTensor(1, 3, 1) >>> y=torch.FloatTensor(3, 1, 7) >>> (x.add_(y)).size() 

 RuntimeError: The expanded size of the tensor (1) must match the existing size (7) at non-singleton dimension 2. 

2番目のケースでは、テンソルは明らかにブロードキャスト可能ですが、インプレース操作は許可されません。これは、その間にxがサイズ変更されるためです。

Numpyから戻って

torch.from_numpy(n)およびx.numpy()を使用して、あるライブラリのテンソルを別のライブラリのテンソルに変換できます。

この場合、テンソルは同じ内部ストレージを使用するため、データのコピーは行われません。

 >>> import torch >>> import numpy as np >>> a = np.random.rand(3, 3) >>> a array([[ 0.3191423 , 0.75283128, 0.31874139], [ 0.0077988 , 0.66912423, 0.3410516 ], [ 0.43789109, 0.39015864, 0.45677317]]) >>> b = torch.from_numpy(a) >>> b 0.3191 0.7528 0.3187 0.0078 0.6691 0.3411 0.4379 0.3902 0.4568 [torch.DoubleTensor of size 3x3] >>> b.sub_(b) 0 0 0 0 0 0 0 0 0 [torch.DoubleTensor of size 3x3] >>> a array([[ 0., 0., 0.], [ 0., 0., 0.], [ 0., 0., 0.]]) 

これに関して、私は考慮されたテンソルライブラリPyTorchのすべての主要な点を考慮することを提案します。 読者が、PyTorchで任意の関数の直接パスを実装することは、NumPyでそれを行うことより難しくないことを理解したことを願っています。 操作をインプレースし、主要な関数の名前を覚えておく必要があります。 たとえば、softmaxアクティベーション機能を備えたラインレイヤー：

 def LinearSoftmax(x, w, b): s = x.mm(w).add_(b) s.exp_() s.div_(s.sum(1)) return s 

クーダ

ここではすべてが単純です。テンソルは、「プロセッサ上」または「ビデオカード上」のどちらでも使用できます。 確かに、彼らは非常に細心の注意を払っており、Nvidiaのビデオカードでのみライブし、最も古いものではありません。 デフォルトでは、テンソルはCPU上に作成されます。

 x = torch.FloatTensor(1024, 1024).uniform_() 

ビデオカードのメモリが空です。

 0MiB / 4036MiB 

1回の呼び出しで、テンソルをGPUに移動できます。

 x = x.cuda() 

同時に、 nvidia-smiは、 pythonプロセスがビデオメモリの一部をnvidia-smiことを示します。

 205MiB / 4036MiB 

x.is_cudaプロパティは、テンソルxが現在どこにあるかを理解するのに役立ちます。

 >>> x.is_cuda True 

実際には、 x.cuda()はテンソルのコピーを返しますが、移動しません。

ビデオメモリ内のテンソルへのすべての参照が消えると、PyTorchはそれを即座に削除しません。 代わりに、次に割り当てられるときに、ビデオメモリのこのセクションを再利用するか、クリアします。

複数のビデオカードがある場合、 x.cuda(device=None)関数x.cuda(device=None)は、テンソルをオプションの引数として配置するビデオカードの番号を喜んで受け入れ、 x.get_device()関数はxテンソルが配置されているデバイスを表示します。 x.cpu()関数は、ビデオカードからプロセッサにテンソルをコピーします。

当然、異なるデバイスにあるテンソルを使用して操作を実行することはできません。

ここでは、たとえば、ビデオカードで2つのテンソルを乗算し、結果をRAMに戻す方法を示します。

 >>> import torch >>> a = torch.FloatTensor(10000, 10000).uniform_() >>> b = torch.FloatTensor(10000, 10000).uniform_() >>> c = a.cuda().mul_(b.cuda()).cpu() 

そして、これらはすべてインタープリターから直接利用できます！ 同じTensorFlowコードを想像してください。ここでは、グラフ、セッションを作成し、グラフをコンパイルし、変数を初期化し、セッションでグラフを実行する必要があります。 PyTorchを使用すると、1行のコードでビデオカードのテンソルを並べ替えることもできます。

テンソルはビデオカードにコピーできるだけでなく、直接作成することもできます。 これを行うには、 torch.cudaモジュールを使用します。

Tensor = FloatTensorという省略形torch.cudaません。

torch.cuda.device(device)コンテキストマネージャーを使用すると、指定されたビデオカードで定義されたすべてのテンソルを作成できます。 他のデバイスからのテンソルに対する操作の結果は、本来あるべき場所に残ります。 x.cuda(device=None)れるx.cuda(device=None) 、コンテキストマネージャーが指示する値よりも高くなっています。

 x = torch.cuda.FloatTensor(1) # x.get_device() == 0 y = torch.FloatTensor(1).cuda() # y.get_device() == 0 with torch.cuda.device(1): a = torch.cuda.FloatTensor(1) # a.get_device() == 1 b = torch.FloatTensor(1).cuda() # a.get_device() == b.get_device() == 1 c = a + b # c.get_device() == 1 z = x + y # z.get_device() == 0 d = torch.FloatTensor(1).cuda(2) # d.get_device() == 2 

CPUのテンソルでのみ使用可能なx.pin_memory()関数は、テンソルをページロックされたメモリ領域にコピーします。 その特徴は、プロセッサーの関与なしに、GPUからのデータをGPUに迅速にコピーできることです。 x.is_pinned()メソッドは、テンソルの現在のステータスを表示します。 テンソルがページロックメモリに格納されx.cuda(device=None, async=False) 、名前付きパラメーターasync=Trueをx.cuda(device=None, async=False)関数にx.cuda(device=None, async=False) 、ビデオカードに非同期でテンソルをロードするように要求できます。 そのため、コードはコピーが完了するのを待たずに、この間に何か役に立つことをするかもしれません。

x.is_pinned() == False場合、 asyncパラメーターは効果がありません。 これによりエラーも発生しません。

ご覧のとおり、ビデオカードでのコンピューティングに任意のコードを適応させるには、すべてのテンソルをビデオメモリにコピーするだけです。 テンソルが同じデバイス上にある場合、ほとんどの操作はテンソルの位置を気にしません。

自動差別化

torch.autogradモジュールに含まれる自動差別化メカニズムは、メインではありませんが、間違いなくライブラリの最も重要なコンポーネントであり、それなしではすべての意味を失います。

特定のポイントでの関数の勾配の計算は、最適化手法の中心的な操作であり、最適化手法はすべてのディープラーニングに基づいています。 ここで学ぶことは最適化と同義です。 ポイントで関数の勾配を計算する主な方法は3つあります。

1. 有限差分法による数値。
2. 象徴的に。
3. 自動微分の手法を使用します。

最初の方法は、精度が低いため、結果を検証するためにのみ使用されます。 導関数の記号計算は、紙と鉛筆を使用して手動で行うのと同等であり、規則のリストを記号ツリーに適用することにあります。 自動差別化については、次の段落で説明します。 CaffeやCNTKなどのライブラリは、事前に計算された関数のシンボリック導関数を使用します。 TheanoとTensorFlowは、方法2と3の組み合わせを使用します。

自動微分（AD）は、関数の勾配を計算するためのかなり単純で非常に明白な手法です。 インターネットを使用せずに、特定の時点で機能を差別化する問題を解決しようとすると、間違いなくADになります。

これがADの仕組みです。 私たちにとって興味のある関数は、いくつかの基本関数の合成として表現することができ、その派生関数は私たちに知られています。 次に、複雑な関数の微分のルールを使用して、目的の導関数に到達するまで次第に高くなります。 たとえば、2つの変数の関数を考えます

$$

$$f（x_1、x_2）= x_1 x_2 + x_1 ^ 2.$$

再指定

$$

$$w_1 = x_1、$$

$$

$$w_2 = x_2、$$

$$

$$w_3 = w_1 w_2、$$

$$

$$w_4 = w_1 ^ 2、$$

$$

$$w_5 = w_3 + w_4$$

— .

,

$$

$$\dfrac{\partial{f(x_1^*, x_2^*)}}{\partial{x_1}}.$$

$$

$$\dfrac{\partial{f}}{\partial{x_1}} = \dfrac{\partial{f}}{\partial{w_5}} \dfrac{\partial{w_5}}{\partial{x_1}} = \dfrac{\partial{f}}{\partial{w_5}} \Big[ \dfrac{\partial{w_5}}{\partial{w_4}} \dfrac{\partial{w_4}}{\partial{x_1}} + \dfrac{\partial{w_5}}{\partial{w_3}} \dfrac{\partial{w_3}}{\partial{x_1}} \Big] = \cdots$$

— — . . , — .

$$

$$\dfrac{\partial{w_1(x_1^*, x_2^*)}}{\partial{x_1}} = 1$$

$$

$$\dfrac{\partial{w_2(x_1^*, x_2^*)}}{\partial{x_1}} = 0$$

$$

$$\dfrac{\partial{w_3(x_1^*, x_2^*)}}{\partial{x_1}} = \dfrac{\partial{w_1(x_1^*, x_2^*)}}{\partial{x_1}} w_2 + \dfrac{\partial{w_2(x_1^*, x_2^*)}}{\partial{x_1}} w_1 = x_2^*$$

$$

$$\dfrac{\partial{w_4(x_1^*, x_2^*)}}{\partial{x_1}} = 2 w_1\dfrac{\partial{w_1(x_1^*, x_2^*)}}{\partial{x_1}} = 2 x_1^*$$

$$

$$\dfrac{\partial{w_5(x_1^*, x_2^*)}}{\partial{x_1}} = \dfrac{\partial{w_3(x_1^*, x_2^*)}}{\partial{x_1}} + \dfrac{\partial{w_4(x_1^*, x_2^*)}}{\partial{x_1}} = x_2^* + 2 x_1^*$$

$$

$$\dfrac{\partial{f(x_1^*, x_2^*)}}{\partial{x_1}} = \dfrac{\partial{f(x_1^*, x_2^*)}}{\partial{w_5}} \dfrac{\partial{w_5(x_1^*, x_2^*)}}{\partial{x_1}} = x_2^* + 2 x_1^*$$

. , . , — , . , — .

AD, 20 Python! . .

 class Varaible: def __init__(self, value, derivative): self.value = value self.derivative = derivative 

, , .

  def __add__(self, other): return Varaible( self.value + other.value, self.derivative + other.derivative ) 

  def __mul__(self, other): return Varaible( self.value * other.value, self.derivative * other.value + self.value * other.derivative ) def __pow__(self, other): return Varaible( self.value ** other, other * self.value ** (other - 1) ) 

x1 .

 def f(x1, x2): vx1 = Varaible(x1, 1) vx2 = Varaible(x2, 0) vf = vx1 * vx2 + vx1 ** 2 return vf.value, vf.derivative print(f(2, 3)) # (10, 7) 

Variable torch.autograd . , , , PyTorch . , , . 例を見てみましょう。

 >>> from torch.autograd import Variable >>> x = torch.FloatTensor(3, 1).uniform_() >>> w = torch.FloatTensor(3, 3).uniform_() >>> b = torch.FloatTensor(3, 1).uniform_() >>> x = Variable(x, requires_grad=True) >>> w = Variable(w) >>> b = Variable(b) >>> y = w.mv(x).add_(b) >>> y Variable containing: 0.7737 0.6839 1.1542 [torch.FloatTensor of size 3] >>> loss = y.sum() >>> loss Variable containing: 2.6118 [torch.FloatTensor of size 1] >>> loss.backward() >>> x.grad Variable containing: 0.2743 1.0872 1.6053 [torch.FloatTensor of size 3] 

: Variable , . x.backward() , requires_grad=True . x.grad . x.data .

, Variable .

x.requires_grad , . : , .

, inplace . , , Variable , . : , immutable . mutable . : PyTorch -, .

例

FaceResNet-1337 . PyTorch, , , . , .

, Deep Function Machines: Generalized Neural Networks for Topological Layer Expression . . , . , , , . :

$$

$$V_n(v) = \int_n^{n+1} (u - n) w_l(u, v) d \mu(u)$$

$$

$$Q_n(v) = \int_n^{n+1} w_l(u, v) d \mu(u)$$

$$

$$W_{n,j} = Q_n(j) - V_n(j) + V_{n-1}(j)$$

$$

$$W_{N, j} = V_{N-1}(j)$$

$$

$$W_{1,j} = Q_1(j) - V_1(j)$$

. w — , W — , . W , - , , w . ? PyTorch — . .

 import numpy as np import torch from torch.autograd import Variable def kernel(u, v, s, w, p): uv = Variable(torch.FloatTensor([u, v])) return s[0] + w.mv(uv).sub_(p).cos().dot(s[1:]) 

.

 def integrate(fun, a, b, N=100): res = 0 h = (b - a) / N for i in np.linspace(a, b, N): res += fun(a + i) * h return res 

.

 def V(v, n, s, w, p): fun = lambda u: kernel(u, v, s, w, p).mul_(u - n) return integrate(fun, n, n+1) def Q(v, n, s, w, p): fun = lambda u: kernel(u, v, s, w, p) return integrate(fun, n, n+1) def W(N, s, w, p): Qp = lambda v, n: Q(v, n, s, w, p) Vp = lambda v, n: V(v, n, s, w, p) W = [None] * N W[0] = torch.cat([Qp(v, 1) - Vp(v, 1) for v in range(1, N + 1)]) for j in range(2, N): W[j-1] = torch.cat([Qp(v, j) - Vp(v, j) + Vp(v, j - 1) for v in range(1, N + 1)]) W[N-1] = torch.cat([ Vp(v, N-1) for v in range(1, N + 1)]) W = torch.cat(W) return W.view(N, N).t() 

.

 s = Variable(torch.FloatTensor([1e-5, 1, 1]), requires_grad=True) w = Variable(torch.FloatTensor(2, 2).uniform_(-1e-5, 1e-5), requires_grad=True) p = Variable(torch.FloatTensor(2).uniform_(-1e-5, 1e-5), requires_grad=True) 

.

 data_x_t = torch.FloatTensor(100, 3).uniform_() data_y_t = data_x_t.mm(torch.FloatTensor([[1, 2, 3]]).t_()).view(-1) 

.

 alpha = -1e-3 for i in range(1000): data_x, data_y = Variable(data_x_t), Variable(data_y_t) Wc = W(3, s, w, p) y = data_x.mm(Wc).sum(1) loss = data_y.sub(y).pow(2).mean() print(loss.data[0]) loss.backward() s.data.add_(s.grad.data.mul(alpha)) s.grad.data.zero_() w.data.add_(w.grad.data.mul(alpha)) w.grad.data.zero_() p.data.add_(p.grad.data.mul(alpha)) p.grad.data.zero_() 

. .

. 3d matplotlib , . , , , 15 . . TensorFlow… , TensorFlow. PyTorch . , PyTorch . , PyTorch , .

.

 data_x, data_y = Variable(data_x_t), Variable(data_y_t) 

, . - , , : .

 loss.backward() 

, , .

 s.data.add_(s.grad.data.mul(alpha)) 

(), . .

 s.grad.data.zero_() 

backward() , .

, : PyTorch , , , Keras.

おわりに

PyTorch: , cuda . PyTorch .

, PyTorch . , . : PyTorch , . , Caffe, DSL TensorFlow. PyTorch , , .

, , torch.nn torch.optim . torch.utils.data . torchvision . .

PyTorch . . - . , . .

読んでくれてありがとう！ , , , . .