地形がオープンスペースでのほとんどのコンピューターゲームの不可欠な部分であると主張するのは困難です。 プレーヤーの周囲の表面のレリーフの変更を実装する従来の方法は次のとおりです-平面であるメッシュ(メッシュ)を取得し、このグリッド内の各プリミティブに対して、このプリミティブに固有の値でこの平面の法線に沿ってシフトします。 簡単に言えば、256 x 256ピクセルの単一チャネルテクスチャと平面グリッドがあります。 各プリミティブについて、平面上の座標により、テクスチャから値を取得します。 ここで、取得した値によって、平面に垂直なプリミティブの座標を単純にシフトします(図1)
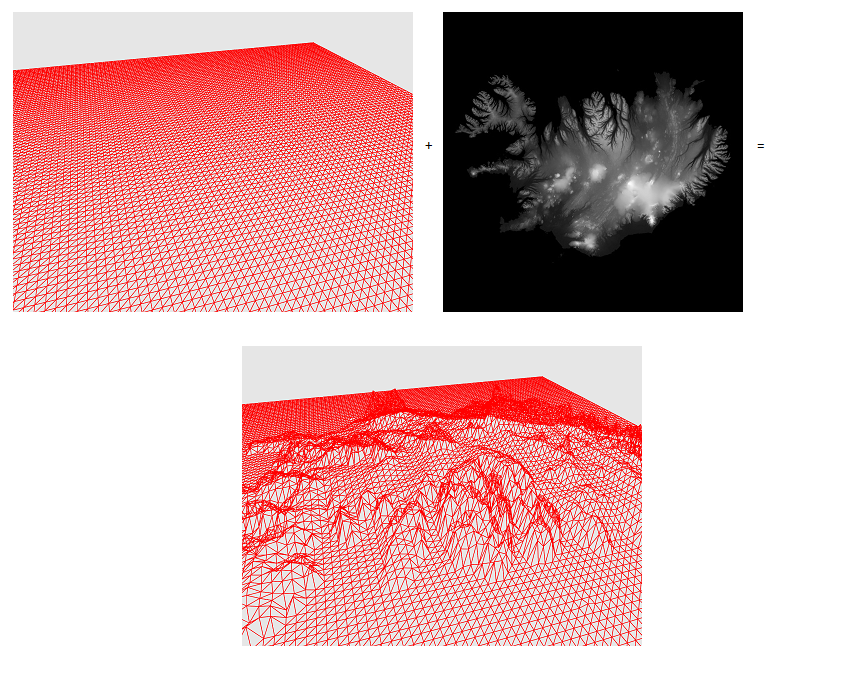 図1標高マップ+平面=地形
図1標高マップ+平面=地形なぜ機能するのですか? プレーヤーが球の表面にあり、この球の半径がプレーヤーのサイズに比べて非常に大きいと想像すると、表面の曲率は無視され、平面が使用されます。 しかし、私たちが球体にいるという事実を無視しないとどうなりますか? この記事では、そのようなランドスケープを構築した経験を読者と共有したいと思います。
1.セクター
明らかに、球体全体のランドスケープをすぐに構築することは賢明ではありません-そのほとんどは表示されません。 したがって、特定のプリミティブの空間の特定の最小限の領域を作成する必要があります。そのプリミティブの球体の可視部分のレリーフが構成されます。 彼のセクターに名前を付けます。 どうやって手に入れますか? したがって、図2aを見てください。 緑のセルは私たちのセクターです。 次に、6つのグリッドを作成します。各グリッドは立方体の面です(図2b)。 次に、グリッドを形成するプリミティブの座標を正規化します(図2c)。
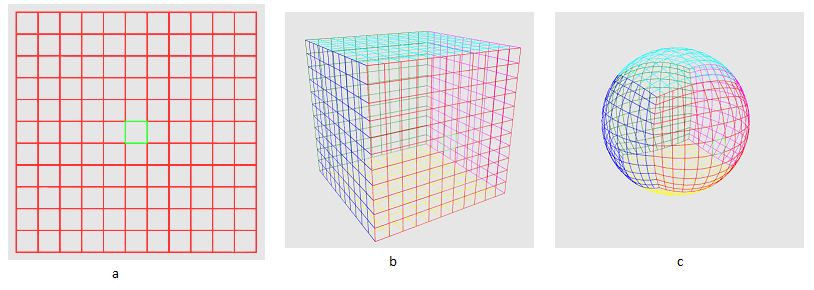 図2
図2その結果、球体に投影された立方体が得られました。ここで、セクターはその面の1つの領域です。 なぜ機能するのですか? グリッド上の任意の点を原点からのベクトルと考えてください。 ベクトル正規化とは何ですか? これは、与えられたベクトルを同じ方向のベクトルに変換しますが、単位長は同じです。 プロセスは次のとおりです。最初に、ピタゴラスの定理に従ってユークリッドメトリックでベクトルの長さを見つけます。

次に、ベクトルの各コンポーネントをこの値で除算します

今、自問してください、球とは何ですか? 球体は、与えられた点から等距離にある点の集合です。 球のパラメトリック方程式は次のようになります
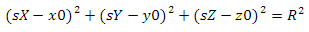
ここで、x0、y0、z0は球の中心の座標、Rはその半径です。 この例では、球体の中心が原点であり、半径は単一です。 既知の値を置き換えて、方程式の2つの部分のルートを取得します。 次のことがわかります

文字通り、最後の変換は次のことを示しています。「球に属するためには、ベクトルの長さは1に等しくなければなりません。」 これが正規化によって達成されたものです。
しかし、球体の中心と半径が任意の場合はどうでしょうか? 次の式を使用して、それに属するポイントを見つけることができます
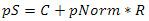
ここで、pSは球上の点、Cは球の中心、pNormは以前に正規化されたベクトル、Rは球の半径です。 簡単な言葉で言えば、ここでは次のことが起こります。「球の中心から距離Rのグリッド上の点に向かって移動します」。 結果として、各ベクトルには単位長があるため、結果として、すべての点は球の中心からその半径の距離だけ等距離になり、球の方程式が真になります。
2.管理
視点から潜在的に見えるセクターのグループを取得する必要があります。 しかし、それを行う方法は? ある点を中心とする球体があるとします。 また、球体にあるセクターと、球体に近い空間にあるポイントPもあります。 次に、2つのベクトルを作成します。1つは球の中心からセクターの中心に向けられ、もう1つは球の中心から視点に向けられます。 図3をご覧ください-これらのベクトル間の角度の絶対値が90度未満の場合にのみ、セクターを見ることができます。
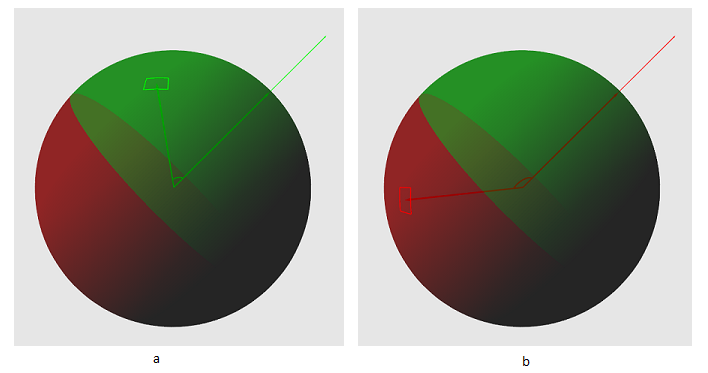 図3 a-90度未満の角度-セクターが潜在的に見える。 b-90度より大きい角度-セクターは表示されません
図3 a-90度未満の角度-セクターが潜在的に見える。 b-90度より大きい角度-セクターは表示されませんこの角度を取得する方法は? これを行うには、ベクトルのスカラー積を使用します。 3次元の場合、次のように計算されます。

スカラー積には分布プロパティがあります。

先ほど、ベクトルの長さの方程式を定義しました-今では、ベクトルの長さは、このベクトル自体のスカラー積のルートに等しいと言えます。 またはその逆-ベクトル自体のスカラー積はその長さの2乗に等しくなります。
それでは、コサインの法則を見てみましょう。 2つの定式化の1つは次のようになります(図4)。

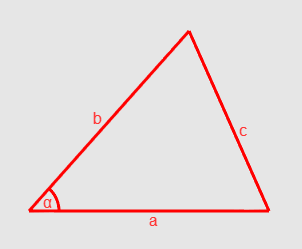 図4コサインの法則
図4コサインの法則ベクトルの長さをaとbとしてとると、角度アルファが探しています。 しかし、どのようにして価値を得るのでしょうか? 見てください:bからaを引くと、aからbに向かうベクトルが得られます。ベクトルは方向と長さだけで特徴付けられるので、ベクトルaの終わりにその開始点をグラフィカルに見つけることができます。 これに基づいて、cはベクトルb-aの長さに等しいと言えます。 だから、私たちは成功しました
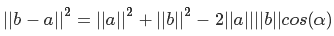
長さの二乗をスカラー積として表現する
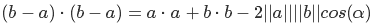
分布プロパティを使用して括弧を開きます
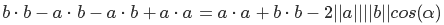
少し切る

そして最後に、方程式の両方の名誉をマイナス2で割ると、
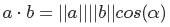
これは、スカラー積のもう1つのプロパティです。 この場合、ベクトルの長さが1になるようにベクトルを正規化する必要があります。 角度を計算する必要はありません-コサイン値で十分です。 ゼロ未満の場合、このセクターは私たちに興味がないと安全に言えます
3.グリッド
プリミティブを描画する方法について考える時が来ました。 先ほど言ったように、セクターは私たちのスキームの主要なコンポーネントであるため、潜在的に見えるセクターごとにグリッドを描き、そのプリミティブがランドスケープを形成します。 各セルは、2つの三角形を使用して表示できます。 各セルには隣接する面があるため、三角形のほとんどの頂点の値は2つ以上のセルに対して繰り返されます。 頂点バッファーのデータを複製しないように、インデックスバッファーを埋めます。 インデックスが使用される場合、グラフィックパイプラインはそれらの助けを借りて、頂点バッファー内のどのプリミティブを処理するかを決定します。 (図5)選択したトポロジは、三角形のリスト(D3D11_PRIMITIVE_TOPOLOGY_TRIANGLELIST)です。
 図5インデックスとプリミティブの視覚表示
図5インデックスとプリミティブの視覚表示セクターごとに個別の頂点バッファーを作成すると、費用がかかりすぎます。 グリッド空間の座標で1つのバッファーを使用する方がはるかに効率的です。つまり、xが列で、yが行です。 しかし、それらからどのようにして球体のポイントを得るのでしょうか? セクターは、特定のポイントSで始まる正方形の領域です。すべてのセクターの顔の長さは同じです。SLenと呼びましょう。 グリッドはセクターの全領域をカバーし、行と列の数も同じです。したがって、セル面の長さを見つけるために、次の方程式を構築できます。
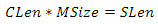
ここで、Lenはセルの面の長さ、MSizeはグリッドの行または列の数です。 両側をMSizeで割り、CLenを取得します

さらに進みます。 セクターが属する立方体の面の空間は、単位長さの2つのベクトルの線形結合として表すことができます-V1およびV2と呼びます。 次の方程式があります(図6を参照)。
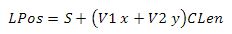
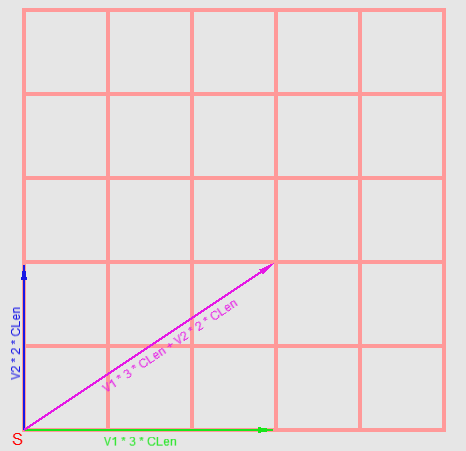 図6グリッド上の点の形成の視覚表示
図6グリッド上の点の形成の視覚表示球上の点を取得するために、先に導出した方程式を使用します
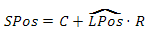
4.高さ
この瞬間に達成したことはすべて、ほとんど風景に似ていません。 高さの違い-それを可能にする何かを追加する時が来ました。 原点を中心とする単位半径の球体と、この球体にある多くのポイント{P0、P1、P2 ... PN}があると想像してください。 これらの各点は、原点からの単位ベクトルとして表すことができます。 ここで、値のセットがあり、それぞれが特定のベクトルの長さであると想像してください(図7)。

これらの値を2次元のテクスチャに保存します。 ピクセルテクスチャの座標と球上の点ベクトルの関係を見つける必要があります。 始めましょう。
デカルト座標に加えて、球体上の点は、球座標系を使用して記述することもできます。 この場合、座標は、方位角、極角、原点からポイントまでの最短距離の値の3つの要素で構成されます。 方位角は、X軸と、原点からXZ平面上の点へのビームの投影との間の角度です。 0〜360度の値を取ることができます。 極角-Y軸と原点から点までの光線との間の角度。 対空または通常と呼ばれることもあります。 0〜180度の値を取ります。 (図8を参照)
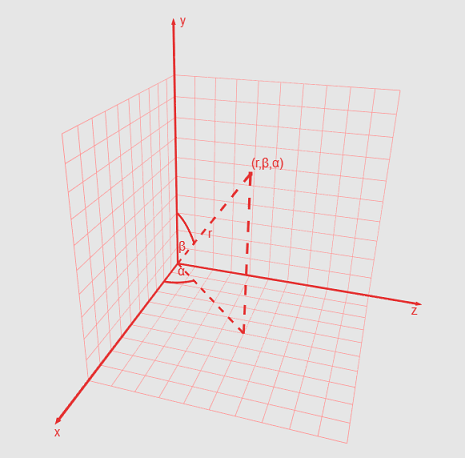 図8球面座標
図8球面座標デカルト系から球面に移動するには、次の式を使用します(Y軸が上向きであると仮定します)。

ここで、dはポイントまでの距離、aは極角、bは方位角です。 パラメータdは、「方程式からわかるように」「原点から点までのベクトルの長さ」として説明することもできます。 正規化された座標を使用すると、極角を見つけるときに分割を回避できます。 実際、なぜこれらの角度が必要なのでしょうか? それぞれを最大範囲で除算して、0から1までの係数を取得し、それらを使用してシェーダーのテクスチャから選択します。 極角の係数を取得する場合、角度が位置する四分の一を考慮する必要があります。 「しかし、xがゼロの場合、式z / xの値は定義されません」と言います。 zがゼロに等しい場合、xの値に関係なく角度はゼロになります。
これらの値に特別なケースを追加しましょう。 正規化された座標(通常)-いくつかの条件を追加します:法線のX値がゼロでZ値がゼロより大きい場合、係数は0.25、XがゼロでZがゼロより小さい場合は0.75になります。 Zの値がゼロでXがゼロより小さい場合、この場合、係数は0.5になります。 これらはすべて、サークルで簡単に確認できます。 しかし、ZがゼロでXがゼロより大きい場合はどうなりますか?その場合、0と1の両方が正しいでしょうか? 1を選択したことを想像してください。まあ、最小方位角0から最大90度のセクターを考えてみましょう。 次に、このセクターが表示するグリッドの最初の行にある最初の3つの頂点を検討します。 最初の頂点については、条件を満たし、テクスチャ座標Xを1に設定します。明らかに、この条件は次の2つの頂点には当てはまりません。 0.1)。 ただし、同じ行の最後の3つの頂点の角度が270〜360のセクターでは、すべてが正しくなります。最後の頂点の条件が機能し、セット(0.9、0.95、1.0)が取得されます。 結果としてゼロを選択すると、セット(0.0、0.05、0.1)と(0.9、0.95、0.0)が得られます-いずれの場合でも、これはかなり顕著な表面の歪みにつながります。 それでは、次を適用しましょう。 セクターの中心を取り、その中心を正規化して、球体に移動します。 次に、ベクトル(0、0、1)によって正規化された中心のスカラー積を計算します。 正式に言えば、このベクトルはXY平面に垂直であり、セクターの中心の正規化されたベクトルとそのスカラー積を計算したので、中心が平面のどちら側にあるかを理解できます。 ゼロより小さい場合、セクターは平面の後ろにあり、値1が必要です。スカラー積がゼロより大きい場合、セクターは平面の前にあるため、境界値は0になります(図9を参照)。
 図9テクスチャ座標に0〜1を選択する問題
図9テクスチャ座標に0〜1を選択する問題以下は、球面からテクスチャ座標を取得するためのコードです。 注意してください-計算のエラーのため、ゼロと等しいかどうかの正常値を確認することはできません。代わりに、それらの絶対値を特定のしきい値(たとえば、0.001)と比較する必要があります
//norm - , //offset - , norm //zeroTreshold - (0.001) float2 GetTexCoords(float3 norm, float3 offset) { float tX = 0.0f, tY = 0.0f; bool normXIsZero = abs(norm.x) < zeroTreshold; bool normZIsZero = abs(norm.z) < zeroTreshold; if(normXIsZero || normZIsZero){ if(normXIsZero && norm.z > 0.0f) tX = 0.25f; else if(norm.x < 0.0f && normZIsZero) tX = 0.5f; else if(normXIsZero && norm.z < 0.0f) tX = 0.75f; else if(norm.x > 0.0f && normZIsZero){ if(dot(float3(0.0f, 0.0f, 1.0f), offset) < 0.0f) tX = 1.0f; else tX = 0.0f; } }else{ tX = atan(norm.z / norm.x); if(norm.x < 0.0f && norm.z > 0.0f) tX += 3.141592; else if(norm.x < 0.0f && norm.z < 0.0f) tX += 3.141592; else if(norm.x > 0.0f && norm.z < 0.0f) tX = 3.141592 * 2.0f + tX; tX = tX / (3.141592 * 2.0f); } tY = acos(norm.y) / 3.141592; return float2(tX, tY); }
頂点シェーダーの中間バージョンを提供します
//startPos - //vec1, vec2 - //gridStep - //sideSize - //GetTexCoords() - VOut ProcessVertex(VIn input) { float3 planePos = startPos + vec1 * input.netPos.x * gridStep.x + vec2 * input.netPos.y * gridStep.y; float3 sphPos = normalize(planePos); float3 normOffset = normalize(startPos + (vec1 + vec2) * sideSize * 0.5f); float2 tc = GetTexCoords(sphPos, normOffset); float height = mainHeightTex.SampleLevel(mainHeightTexSampler, tc, 0).x; posL = sphPos * (sphereRadius + height); VOut output; output.posH = mul(float4(posL, 1.0f), worldViewProj); output.texCoords = tc; return output; }
5.照明
風景の色の照明依存性を実現するために、次の式を使用します。

ここで、Iはポイントの色、Ldは光源の色、Kdは照明された表面の材料の色、aは光源のベクトルと照明された表面の法線との間の角度です。 これは、ランバートのコサインの法則の特別な場合です。 ここにあるものとその理由を見てみましょう。 LdとKdの乗算は、色の成分ごとの乗算、つまり(Ld.r * Kd.r、Ld.g * Kd.g、Ld.b * Kd.b)を意味します。 次の状況を想像すると、意味を理解しやすくなる場合があります。オブジェクトを緑色の光源で照らしたい場合、オブジェクトの色は緑色のグラデーションになると想定します。 結果(0 * Kd.r、1 * Kd.g、0 * Kd.b)は(0、Kd.g、0)-まさに必要なものを与えます。 さらに進みます。 前述のように、正規化されたベクトル間の角度の余弦は、それらのスカラー積です。 私たちの観点からその最大値と最小値を考えてみましょう。 ベクトル間の角度の余弦が1の場合、この角度は0です。したがって、両方のベクトルは同一直線上にあります(同じ線上にあります)。
同じことがコサイン-1の値にも当てはまります。この場合のみ、ベクトルは反対方向を指します。 法線ベクトルと光源へのベクトルが共線性状態に近いほど、法線が属する表面の照明係数が高くなることがわかります。 また、その法線が光源への方向に対して反対方向を向いている場合、表面を照らすことはできないと想定されています。そのため、正のコサイン値のみを使用します。
私はパラレルソースを使用しているため、その位置は無視できます。 考慮すべき唯一のことは、光源にベクトルを使用することです。 つまり、光線の方向(1.0、-1.0、0)であれば、ベクトル(-1.0、1.0、0)を使用する必要があります。 私たちにとって難しいのは、法線ベクトルだけです。 平面の法線を計算するのは簡単です-それを記述する2つのベクトルのベクトル積を生成する必要があります。 ベクトル積は反可換であることに注意することが重要です-因子の順序を考慮する必要があります。 この場合、次のように、グリッド空間内の頂点の座標を知って、三角形の法線を取得できます(pxとpyの境界ケースを考慮していないことに注意してください)
float3 p1 = GetPosOnSphere(p); float3 p2 = GetPosOnSphere(float2(px + 1, py)); float3 p3 = GetPosOnSphere(float2(px, py + 1)); float3 v1 = p2 - p1; float3 v2 = p3 - p1; float3 n = normalzie(cross(v1, v2));
しかし、それだけではありません。 ほとんどのグリッド頂点は、一度に4つの平面に属します。 許容できる結果を得るには、次のように平均法線を計算する必要があります。
Na = normalize(n0 + n1 + n2 + n3)
GPUでこのメソッドを実装するのは非常に高価です。法線とその平均化を計算するには2つのステップが必要です。 さらに、有効性は低いです。 これに基づいて、別の方法を選択しました-法線マップを使用します(図10)。
 図10法線マップ
図10法線マップこれを使用する原理は、高さマップと同じです-メッシュ頂点の球座標をテクスチャに変換し、選択を行います。 このデータを直接使用することはできません-球体を使用しており、頂点には独自の法線があり、これを考慮する必要があります。 したがって、法線マップデータを基底のTBN座標として使用します。 根拠は何ですか? 以下に例を示します。 あなたが宇宙飛行士であり、宇宙のどこかにある灯台に座っていると想像してください。 MCCから「ビーコンから1メートル左、2メートル上、3メートル前方に移動する必要があります」というメッセージが表示されます。 これはどのように数学的に表現できますか? (1、0、0)* 1 +(0、1、0)* 2 +(0、0、1)* 3 =(1,2,3)。 行列形式では、この方程式は次のように表現できます。
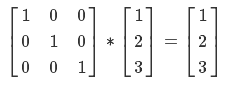
今、あなたが灯台にも座っていると想像してみてください。MCCからあなたに書かれたのは、「方向ベクトルを送信しました。最初のベクトルで1メートル、2番目で2メートル、3番目で3メートル進む必要があります」。 新しい座標の方程式は次のようになります。
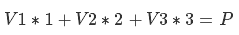
展開されたエントリは次のようになります。
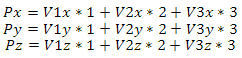
またはマトリックス形式で:

したがって、ベクトルV1、V2、およびV3の行列は基底であり、ベクトル(1,2,3)はこの基底の空間内の座標です。
一連のベクトル(基底M)があり、ビーコンに対する相対的な位置(ポイントP)がわかっていることを想像してください。 この基礎の空間での座標を知る必要があります-同じ場所にいるためにこれらのベクトルに沿ってどれだけ前進する必要があるか。 目的の座標を想像してください(X)
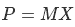
P、M、およびXが数値の場合、単純に方程式の両側をMで分離しますが、悲しいかな...逆行列のプロパティに従って、逆になります。
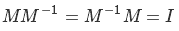
ここで、Iは単位行列です。 私たちの場合、このように見えます

これにより何が得られますか? この行列にXを掛けると、
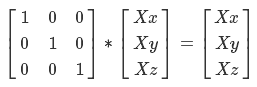
また、行列の乗算には結合性の特性があることを明確にする必要があります。

ベクトルを3行1列の行列として非常に正しく考えることができます。
上記のすべてを考えると、式の右側にXを取得するために、正しい順序で両側に逆M行列を乗算する必要があると結論付けることができます

今後この結果が必要になります。
問題に戻りましょう。 正規直交基底を使用します-これは、V1、V2、およびV3が互いに直交(90度の角度を形成)し、単位長さを持つことを意味します。 接線ベクトルは、V1、V2-二重接線ベクトル、V3-法線として機能します。 従来のDirectX転置ビューでは、マトリックスは次のようになります。
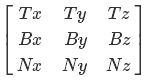
ここで、Tは接線ベクトル、Bは両接線ベクトル、Nは法線です。 それらを見つけましょう。 通常、最も簡単な方法は、実際、これらはポイントの正規化された座標です。 Bitangentベクトルは、法線ベクトル積と接線ベクトルに等しくなります。 最も難しいのは、接線ベクトルを使用することです。 これは、ある点での円の接線の方向に等しくなります。 この瞬間を見てみましょう。 まず、ある角度aについてXZ平面の単位円上の点の座標を見つけます
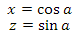
この点での円の接線の方向は、2つの方法で見つけることができます。 円上の点へのベクトルと接線ベクトルは直交します-したがって、関数sinとcosは周期的であるため、単純にpi / 2を角度aに追加して、目的の方向を取得できます。 pi / 2のoffsetプロパティによると:
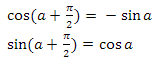
次のベクターがあります。

微分を使用することもできます-詳細については、付録3を参照してください。したがって、図11で、各頂点の基底が構築される球体を見ることができます。 青いベクトルは法線、赤は接線ベクトル、緑は両方向ベクトルです。
 図11各頂点にTBNベースを持つ球。 赤-接線ベクトル、緑-二方向ベクトル、青ベクトル-通常
図11各頂点にTBNベースを持つ球。 赤-接線ベクトル、緑-二方向ベクトル、青ベクトル-通常基礎を理解しました-さて、法線マップを取得しましょう。 これを行うには、Sobelフィルターを使用します。 Sobelフィルターは、各ポイント(大まかに言えば、輝度変化ベクトル)で画像の輝度勾配を計算します。 フィルターの原理は、「コア」と呼ばれる特定の値のマトリックスを、このマトリックスの次元内の各ピクセルとその隣接ピクセルに適用する必要があるということです。 カーネルKでピクセルPを処理するとします。画像の境界にない場合、左上、上、右上などの8つの隣接ピクセルがあります。 それらをtl、t、tb、l、r、bl、b、brと呼びます。 したがって、このピクセルにKカーネルを適用することは次のとおりです。
Pn = tl * K(0、0)+ t * K(0,1)+ tb * K(0,2)+
&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbspl * K(1、0)+ P * K(1,1)+ r * K(1,2)+
&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbspbl * K(2、0)+ b * K(2,1)+ br * K(2,2)
このプロセスは「畳み込み」と呼ばれます。 Sobelフィルターは2つのコアを使用して、垂直方向と水平方向の勾配を計算します。 それらをKxおよびKとして示します。
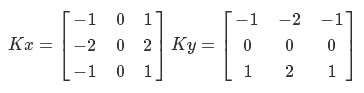
基礎があります-実装を開始できます。 まず、ピクセルの明るさを計算する必要があります。 PALシステムでは、RGBカラーモデルからYUVモデルへの変換を使用します。
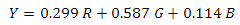
ただし、画像は元々グレースケールであったため、この手順は省略できます。 ここで、KxおよびKyカーネルを使用して元のイメージを「縮小」する必要があります。 したがって、XおよびYグラデーションのコンポーネントを取得します。 このベクトルの法線値も非常に有用です-使用しませんが、正規化された勾配法線の値を含む画像にはいくつかの有用な用途があります。 正規化とは、次の方程式を意味します

ここで、Vは正規化する値、VminとVmaxはこれらの値の範囲です。 この場合、最小値と最大値は生成プロセス中に追跡されます。 Sobelフィルターの実装例は次のとおりです。
float SobelFilter::GetGrayscaleData(const Point2 &Coords) { Point2 coords; coords.x = Math::Saturate(Coords.x, RangeI(0, image.size.width - 1)); coords.y = Math::Saturate(Coords.y, RangeI(0, image.size.height - 1)); int32_t offset = (coords.y * image.size.width + coords.x) * image.pixelSize; const uint8_t *pixel = &image.pixels[offset]; return (image.pixelFormat == PXL_FMT_R8) ? pixel[0] : (0.30f * pixel[0] +
ソーベルフィルターには線形分離性の特性があるため、この方法を最適化できると言わなければなりません。
難しい部分は終わりました-法線マップのピクセルのRチャンネルとGチャンネルの勾配方向のX座標とY座標を書き留める必要がありますZ座標には1つ使用します。 また、3次元の係数ベクトルを使用してこれらの値を調整します。 以下は、コメント付きの法線マップを生成する例です。
次に、シェーダーで法線マップを使用する例を示します。
6.詳細レベル
さて、今私たちの風景がライトアップされています! 月に飛ぶことができます-高さマップを点灯し、マテリアルの色を設定し、セクターをロードし、グリッドサイズを{16、16}に設定します...はい、何かが足りません-{256、256}を入れます-ああ、何かが遅くなります、そしてなぜ遠方セクターでの詳細度が高いのですか? さらに、観測者が惑星に近ければ近いほど、見ることができるセクターは少なくなります。 はい...まだやるべきことがたくさんあります! 最初に、余分なセクターをカットする方法を見つけましょう。 ここで決定する値は、惑星の表面からの観測者の高さです-高いほど、より多くのセクターを見ることができます(図12)
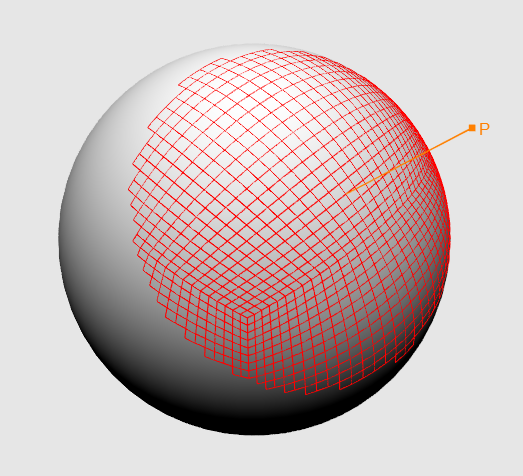 図12観測者の身長の処理済みセクター数への依存性
図12観測者の身長の処理済みセクター数への依存性次のように高さを見つけます-球体の中心にある観測者の位置からベクトルを構築し、その長さを計算して、球体の半径の値をそこから減算します。 前に、オブザーバーによるベクトルとセクターの中心によるベクトルのスカラー積がゼロ未満である場合、このセクターは関心がありません-今ではゼロではなく、高さに線形に依存する値を使用します。 まず、変数を決定しましょう。スカラー積の最小値と最大値、および高さの最小値と最大値を取得します。 次の方程式系を構築します
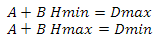
2番目の方程式でAを表現する
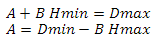
2番目の方程式のAを最初の方程式に代入します
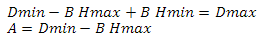
最初の方程式からBを表現する
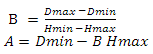
最初の方程式のBを2番目の方程式に代入します
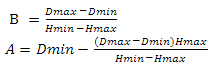
次に、関数の変数を置き換えます

そして得る
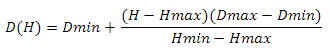
ここで、HminとHmaxは高さの最小値と最大値、DminとDmaxはスカラー積の最小値と最大値です。 この問題は別の方法で解決できます-付録4を参照してください。
次に、詳細レベルを理解する必要があります。 それぞれがスカラー積の範囲を決定します。 擬似コードでは、特定のレベルでセクターのメンバーシップを決定するプロセスは次のようになります。
,
各レベルの値の範囲を計算する必要があります。 まず、2つの方程式のシステムを構築します
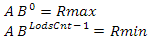
それを解決して、私たちは得る
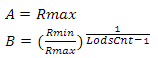
これらの係数を使用して、関数を定義します

ここで、Rmaxはスカラー積のドメイン(D(H)-Dmin)、Rminはレベルによって決定される最小領域です。 0.01の値を使用します。 次に、Dmaxから結果を減算する必要があります

この関数を使用して、すべてのレベルのエリアを取得します。 以下に例を示します。
const float dotArea = dotRange.maxVal - dotRange.minVal; const float Rmax = dotArea, Rmin = 0.01f; float lodsCnt = lods.size(); float A = Rmax; float B = powf(Rmin / Rmax, 1.0f / (lodsCnt - 1.0f)); for(size_t g = 0; g < lods.size(); g++){ lods[g].dotRange.minVal = dotRange.maxVal - A * powf(B, g); lods[g].dotRange.maxVal = dotRange.maxVal - A * powf(B, g + 1); } lods[lods.size() - 1].dotRange.maxVal = 1.0f;
これで、セクターがどの詳細レベルに属するかを判断できます(図13)。
 図13詳細レベルに応じたセクターの色の区別
図13詳細レベルに応じたセクターの色の区別次に、グリッドのサイズを把握する必要があります。 レベルごとにグリッドを維持するのは非常に高価です。テッセレーションを使用して1つのグリッドの詳細をオンザフライで変更する方がはるかに効率的です。 これを行うには、通常の頂点とピクセルに加えて、ハルシェーダーとドメインシェーダーも実装する必要があります。 ハルシェーダーの主なタスクは、ブレークポイントを準備することです。 これは、メイン関数とコントロールポイントのパラメーターを計算する関数の2つの部分で構成されています。 次の属性の値を必ず指定してください。
ドメイン
分割
出力トポロジー
出力制御点
patchconstantfunc
三角測量用のハルシェーダーの例を次に示します。
struct PatchData { float edges[3] : SV_TessFactor; float inside : SV_InsideTessFactor; }; PatchData GetPatchData(InputPatch<VIn, 3> Patch, uint PatchId : SV_PrimitiveID) { PatchData output; flloat tessFactor = 2.0f; output.edges[0] = tessFactor; output.edges[1] = tessFactor; output.edges[2] = tessFactor; output.inside = tessFactor; return output; } [domain("tri")] [partitioning("integer")] [outputtopology("triangle_cw")] [outputcontrolpoints(3)] [patchconstantfunc("GetPatchData")] VIn ProcessHull(InputPatch<VIn, 3> Patch, uint PointId : SV_OutputControlPointID, uint PatchId : SV_PrimitiveID) { return Patch[PointId]; }
ご覧のとおり、主な作業はGetPatchData()で行われます。 そのタスクは、テッセレーション係数を確立することです。 後で説明しますが、今度はドメインシェーダーに進みます。 ハルシェーダーから制御点を受け取り、テッセレーターから座標を受け取ります。 三角形の場合の位置またはテクスチャ座標の新しい値は、次の式を使用して計算する必要があります
N = C1 * Fx + C2 * Fy + C3 * Fz
ここで、C1、C2、およびC3は制御点の値、Fはテッセレータの座標です。 また、ドメインシェーダーでは、Hullシェーダーで指定された値に対応する値を持つドメイン属性を設定する必要があります。 ドメインシェーダーの例を次に示します。
cbuffer buff0 : register(b0) { matrix worldViewProj; } struct PatchData { float edges[3] : SV_TessFactor; float inside : SV_InsideTessFactor; }; [domain("quad")] PIn ProcessDomain(PatchData Patch, float3 Coord : SV_DomainLocation, const OutputPatch<VIn, 3> Tri) { float3 posL = Tri[0].posL * Coord.x + Tri[1].posL * Coord.y + Tri[2].posL * Coord.z; float2 texCoords = Tri[0].texCoords * Coord.x + Tri[1].texCoords * Coord.y + Tri[2].texCoords * Coord.z; PIn output; output.posH = mul(float4(posL, 1.0f), worldViewProj); output.normalW = Tri[0].normalW; output.texCoords = texCoords; return output; }
この場合の頂点シェーダーの役割は最小限に抑えられています-私にとっては、データを次の段階に「投げる」だけです。
次に、同様のものを実装する必要があります。 私たちの主なタスクは、テッセレーション係数を計算することです。より正確には、オブザーバの身長への依存性を構築します。 再び方程式系を構築します
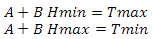
以前と同じ方法で解決すると、
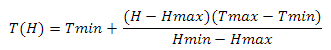
ここで、TminとTmaxはテッセレーション係数の最小値と最大値、HminとHmaxは観測者の高さの最小値と最大値です。 私の最小テッセレーション係数は1です。 最大値はレベルごとに個別に設定されます
(例:1、2、4、16)。
将来的には、因子の成長を最も近い2のべき乗に制限する必要があります。
つまり、2〜3の値の場合、値を2に設定します。4〜7の値の場合、4を設定します。8〜15の値の場合、係数は8になります。要因6についてこの問題を解きましょう。まず、次の方程式を解き ます。対数の
ます。対数の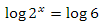 特性に従って方程式の2つの部分の10進数の対数を取り
特性に従って方程式の2つの部分の10進数の対数を取り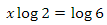 ます。両方の部分をlog(2)
ます。両方の部分をlog(2)
しかし、それだけではありません。
Xは約2.58です。次に、小数部分をリセットし、デュースを結果の数値のべき乗する必要があります。詳細レベルのテッセレーション係数計算コードは次のとおりです float h = camera->GetHeight(); const RangeF &hR = heightRange; for(LodsStorage::Lod &lod : lods){
7.ノイズ
高さマップのサイズを変更せずに、ランドスケープのディテールを増やす方法を見てみましょう。次のことが思い浮かびます-高さの値をグラデーションノイズテクスチャから取得した値に変更します。サンプリングする座標は、メイン座標のN倍になります。フェッチするとき、アドレス指定のミラータイプ(D3D11_TEXTURE_ADDRESS_MIRROR)が使用されます(図14を参照)。 図14高さマップのある球+ノイズマップのある球=全高のある球この場合、高さは次のように計算されます。
図14高さマップのある球+ノイズマップのある球=全高のある球この場合、高さは次のように計算されます。
これまでのところ、周期的な性質は大幅に表現されていますが、照明とテクスチャリングの追加により、状況はより良く変化します。そして、グラデーションノイズテクスチャとは何ですか?大まかに言って、これはランダムな値の格子です。ラティスのサイズをテクスチャのサイズに合わせる方法を見てみましょう。サイズ256 x 256ピクセルのノイズテクスチャを作成するとします。グリルの寸法がテクスチャのサイズと一致する場合、それは簡単です-テレビでホワイトノイズのようなものが得られます。しかし、グリッドに2 x 2の次元がある場合はどうでしょうか?答えは簡単です-補間を使用します。線形補間の定式化の1つは次のとおりです。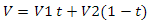 これは最速ですが、同時に私たちにとっては最適なオプションではありません。コサインベースの補間を使用することをお勧めします。
これは最速ですが、同時に私たちにとっては最適なオプションではありません。コサインベースの補間を使用することをお勧めします。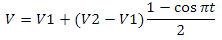 ただし、対角線の端(セルの左下隅と右上隅)に沿って値を単純に補間することはできません。この場合、補間を2回適用する必要があります。格子のセルの1つを紹介しましょう。彼女には4つのコーナーがあります。それらをV1、V2、V3、V4と呼びましょう。また、このセル内には独自の2次元座標系があり、ポイント(0、0)はV1に対応し、ポイント(1、1)はV3に対応します(図15aを参照)。座標(0.5、0.5)で値を取得するには、最初にV1とV4の間、V2とV3の間の2つのX補間値を取得し、最後にこれらの値の間でYに補間する必要があります(図15b)。
ただし、対角線の端(セルの左下隅と右上隅)に沿って値を単純に補間することはできません。この場合、補間を2回適用する必要があります。格子のセルの1つを紹介しましょう。彼女には4つのコーナーがあります。それらをV1、V2、V3、V4と呼びましょう。また、このセル内には独自の2次元座標系があり、ポイント(0、0)はV1に対応し、ポイント(1、1)はV3に対応します(図15aを参照)。座標(0.5、0.5)で値を取得するには、最初にV1とV4の間、V2とV3の間の2つのX補間値を取得し、最後にこれらの値の間でYに補間する必要があります(図15b)。以下に例を示します。
float2 coords(0.5f, 0.5f) float4 P1 = lerp(V1, V4, coords.x); float4 P2 = lerp(V2, V3, coords.x); float4 P = lerp(P1, P2, coords.y)
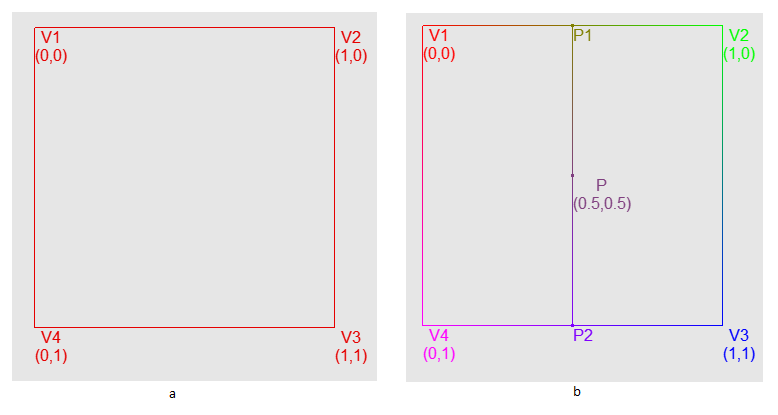 図15a-座標V1、V2、V3、V4の格子セルの画像。b-セルの例での2つの補間のシーケンス、次を実行しましょう-ノイズテクスチャのピクセルごとに、2x4グリッドの補間値を取得し、4x4グリッドの補間値を0.5倍してから、8x4グリッドの0.25倍などを追加します。 q一定の制限-これはオクターブの追加と呼ばれます(図16)。
図15a-座標V1、V2、V3、V4の格子セルの画像。b-セルの例での2つの補間のシーケンス、次を実行しましょう-ノイズテクスチャのピクセルごとに、2x4グリッドの補間値を取得し、4x4グリッドの補間値を0.5倍してから、8x4グリッドの0.25倍などを追加します。 q一定の制限-これはオクターブの追加と呼ばれます(図16)。式は次のとおりです。

 図16オクターブを追加する例以下に実装例を示します。
図16オクターブを追加する例以下に実装例を示します。 for(int32_t x = 0; x < size.width; x++) for(int32_t y = 0; y < size.height; y++){ float val = 0.0f; Vector2 normPos = {(float)x / (float)(sideSize - 1), (float)y / (float)(sideSize - 1)}; for(int32_t o = 0; o < octavesCnt; o++){ float frequency = powf(2.0f, (float)(startFrequency + o)); float intencity = powf(intencityFactor, (float)o); Vector2 freqPos = normPos * frequency; Point2 topLeftFreqPos = Cast<Point2>(freqPos); Point2 btmRightFreqPos = topLeftFreqPos + Point2(1, 1); float xFrac = freqPos.x - (float)topLeftFreqPos.x; float yFrac = freqPos.y - (float)topLeftFreqPos.y; float iVal = GetInterpolatedValue(topLeftFreqPos, btmRightFreqPos, xFrac, yFrac); val += iVal * intencity; } noiseValues[y * size.width + x] = val; }
また、V1、V2、V3、およびV4の場合、次のように値自体とその近傍から合計を取得できます。 float GetSmoothValue(const Point2 &Coords) { float corners = (GetValue({Coords.x - 1, Coords.y - 1}) + GetValue({Coords.x + 1, Coords.y - 1}) + GetValue({Coords.x - 1, Coords.y + 1}) + GetValue({Coords.x + 1, Coords.y + 1})) / 16.0f; float sides = (GetValue({Coords.x - 1, Coords.y}) + GetValue({Coords.x + 1, Coords.y}) + GetValue({Coords.x, Coords.y - 1}) + GetValue({Coords.x, Coords.y + 1})) / 8.0f; float center = GetValue(Coords) / 4.0f; return center + sides + corners; }
これらの値を補間に使用します。コードの残りは次のとおりです。 float GetInterpolatedValue(const Point2 &TopLeftCoord, const Point2 &BottomRightCoord, float XFactor, float YFactor) { Point2 tlCoords(TopLeftCoord.x, TopLeftCoord.y); Point2 trCoords(BottomRightCoord.x, TopLeftCoord.y); Point2 brCoords(BottomRightCoord.x, BottomRightCoord.y); Point2 blCoords(TopLeftCoord.x, BottomRightCoord.y); float tl = (useSmoothValues) ? GetSmoothValue(tlCoords) : GetValue(tlCoords); float tr = (useSmoothValues) ? GetSmoothValue(trCoords) : GetValue(trCoords); float br = (useSmoothValues) ? GetSmoothValue(brCoords) : GetValue(brCoords); float bl = (useSmoothValues) ? GetSmoothValue(blCoords) : GetValue(blCoords); float bottomVal = Math::CosInterpolation(bl, br, XFactor); float topVal = Math::CosInterpolation(tl, tr, XFactor); return Math::CosInterpolation(topVal, bottomVal, YFactor); }
サブセクションの終わりに、ここまで説明してきたことはすべて、Perlinのノイズの実装が標準的な実装とは少し異なることを言いたいと思います。高さを計算しました。次に、法線の処理方法を見てみましょう。メインの高さマップの場合と同様に、ノイズテクスチャから法線マップを生成する必要があります。次に、シェーダーで、メインカードの法線とノイズテクスチャの法線を追加します。これは完全に正しいわけではありませんが、受け入れられる結果をもたらすと言わなければなりません。以下に例を示します。
8.ハードウェアのインスタンス化
最適化をしましょう。擬似コードでセクターを描画するサイクルは次のようになります S V1 V2
このアプローチのパフォーマンスは非常に小さいです。いくつかの最適化オプションがあります-各セクターのスカラー積を計算しないように、キューブの各プレーンにクアッドツリーを構築できます。 V1とV2の値は、各セクターではなく、それらが属するキューブの6つの平面に対しても更新できます。 3番目のオプション-Instancingを選択しました。それが何であるかについて簡単に説明します。森を描きたいとしましょう。ツリーモデルがあり、ツリーの位置、可能なスケーリングまたは回転-変換マトリックスのセットもあります。ワールドスペースに変換されたすべてのツリーの最上部を含む1つのバッファを作成できます-これは良いオプションです。フォレストはマップ上で実行されません。しかし、変換を実装する必要がある場合はどうでしょうか-たとえば、風に揺れる木。これを行うことができます-モデルの頂点のデータをN回1つのバッファーにコピーし、ツリーインデックス(0からN)を頂点データに追加します。次に、変換行列の配列を更新し、変数としてシェーダーに渡します。シェーダーで、ツリーインデックスによって目的のマトリックスを選択します。データの重複をどのように回避できますか?最初に、これらの頂点がいくつかのバッファから収集できるという事実に注意を喚起したいと思います。頂点を記述するには、D3D11_INPUT_ELEMENT_DESC構造体のInputSlotフィールドにソースインデックスを指定する必要があります。これは、モーフィングフェイシャルアニメーションを実装するときに使用できます。2つのフェース状態を含む2つの頂点バッファーがあり、これらの値を線形に補間するとします。トップを説明する方法は次のとおりです。次に、変換行列の配列を更新し、変数としてシェーダーに渡します。シェーダーで、ツリーインデックスによって目的のマトリックスを選択します。データの重複をどのように回避できますか?最初に、これらの頂点がいくつかのバッファから収集できるという事実に注意を喚起したいと思います。頂点を記述するには、D3D11_INPUT_ELEMENT_DESC構造体のInputSlotフィールドにソースインデックスを指定する必要があります。これは、モーフィングフェイシャルアニメーションを実装するときに使用できます。2つのフェース状態を含む2つの頂点バッファーがあり、これらの値を線形に補間するとします。トップを説明する方法は次のとおりです。次に、変換行列の配列を更新し、変数としてシェーダーに渡します。シェーダーで、ツリーインデックスによって目的のマトリックスを選択します。データの重複をどのように回避できますか?最初に、これらの頂点がいくつかのバッファから収集できるという事実に注意を喚起したいと思います。頂点を記述するには、D3D11_INPUT_ELEMENT_DESC構造体のInputSlotフィールドにソースインデックスを指定する必要があります。これは、モーフィングフェイシャルアニメーションを実装するときに使用できます。2つのフェース状態を含む2つの頂点バッファーがあり、これらの値を線形に補間するとします。トップを説明する方法は次のとおりです。頂点を記述するには、D3D11_INPUT_ELEMENT_DESC構造体のInputSlotフィールドにソースインデックスを指定する必要があります。これは、モーフィングフェイシャルアニメーションを実装するときに使用できます。2つのフェース状態を含む2つの頂点バッファーがあり、これらの値を線形に補間するとします。トップを説明する方法は次のとおりです。頂点を記述するには、D3D11_INPUT_ELEMENT_DESC構造体のInputSlotフィールドにソースインデックスを指定する必要があります。これは、モーフィングフェイシャルアニメーションを実装するときに使用できます。2つのフェース状態を含む2つの頂点バッファーがあり、これらの値を線形に補間するとします。トップを説明する方法は次のとおりです。 D3D11_INPUT_ELEMENT_DESC desc[] = { {"POSITION", 0, DXGI_FORMAT_R32G32B32_FLOAT, 0, 0, D3D11_INPUT_PER_VERTEX_DATA, 0}, {"NORMAL", 0, DXGI_FORMAT_R32G32B32_FLOAT, 0, 12, D3D11_INPUT_PER_VERTEX_DATA, 0}, {"TEXCOORD", 0, DXGI_FORMAT_R32G32B32_FLOAT, 0, 24, D3D11_INPUT_PER_VERTEX_DATA, 0}, {"POSITION", 1, DXGI_FORMAT_R32G32B32_FLOAT, 1, 0, D3D11_INPUT_PER_VERTEX_DATA, 0}, {"NORMAL", 1, DXGI_FORMAT_R32G32B32_FLOAT, 1, 12, D3D11_INPUT_PER_VERTEX_DATA, 0}, {"TEXCOORD", 1, DXGI_FORMAT_R32G32B32_FLOAT, 1, 24, D3D11_INPUT_PER_VERTEX_DATA, 0} }
シェーダーでは、頂点を次のように記述する必要があります。 struct VIn { float3 position1 : POSITION0; float3 normal1 : NORMAL0; float2 tex1 : TEXCOORD0; float3 position2 : POSITION1; float3 normal2 : NORMAL1; float2 tex2 : TEXCOORD1; }
次に、値を補間するだけです float3 res = lerp(input.position1, input.position2, factor);
なぜこれをしているのですか?
木の例に戻りましょう。2つのソースから頂点を収集します。最初のソースにはローカル空間の位置、テクスチャ座標、法線が含まれ、2番目のソースには4つの4次元ベクトルの形式の変換マトリックスが含まれます。頂点の説明は次のようになります。 D3D11_INPUT_ELEMENT_DESC desc[] = { {"POSITION", 0, DXGI_FORMAT_R32G32B32_FLOAT, 0, 0, D3D11_INPUT_PER_VERTEX_DATA, 0}, {"NORMAL", 0, DXGI_FORMAT_R32G32B32_FLOAT, 0, 12, D3D11_INPUT_PER_VERTEX_DATA, 0}, {"TEXCOORD", 0, DXGI_FORMAT_R32G32B32_FLOAT, 0, 24, D3D11_INPUT_PER_VERTEX_DATA, 0}, {"WORLD", 0, DXGI_FORMAT_R32G32B32A32_FLOAT, 1, 0, D3D11_INPUT_PER_INSTANCE_DATA, 1}, {"WORLD", 1, DXGI_FORMAT_R32G32B32A32_FLOAT, 1, 16, D3D11_INPUT_PER_INSTANCE_DATA, 1}, {"WORLD", 2, DXGI_FORMAT_R32G32B32A32_FLOAT, 1, 32, D3D11_INPUT_PER_INSTANCE_DATA, 1}, {"WORLD", 3, DXGI_FORMAT_R32G32B32A32_FLOAT, 1, 48, D3D11_INPUT_PER_INSTANCE_DATA, 1}, }
2番目の部分では、InputSlotClassフィールドはD3D11_INPUT_PER_INSTANCE_DATAであり、InstanceDataStepRateフィールドは1であることに注意してください(InstanceDataStepRateフィールドの簡単な説明については、付録1を参照してください)。この場合、コレクターは、タイプD3D11_INPUT_PER_INSTANCE_DATAのソースからの各要素に対して、タイプD3D11_INPUT_PER_VERTEX_DATAのソースからのバッファー全体のデータを使用します。シェーダーでは、これらの頂点は次のように記述できます。 struct VIn { float3 posL : POSITION; float3 normalL : NORMAL; float2 tex : TEXCOORD; row_major float4x4 world : WORLD; };
属性D3D11_USAGE_DYNAMICおよびD3D11_CPU_ACCESS_WRITEで2番目のバッファーを作成することにより、CPU側から更新できます。この種のジオメトリを描画するには、DrawInstanced()またはDrawIndexedInstanced()を呼び出す必要があります。DrawInstancedIndirect()およびDrawIndexedInstancedIndirect()への呼び出しもあります-それらについては、付録2を参照してください。バッファの設定とDrawIndexedInstanced()関数の使用例は次のとおりです。
最後に、トピックに戻りましょう。セクターが属する平面上の点と、この平面を記述する2つのベクトルを使用して、セクターを手動で記述します。したがって、ピークは2つのソースで構成されます。1つ目はグリッド空間の座標、2つ目はセクターデータです。頂点の説明は次のようになります。 std::vector<D3D11_INPUT_ELEMENT_DESC> meta = {
座標をグリッド空間に格納するために、3次元ベクトルを使用していることに注意してください(z座標は使用されません)9.錐台カリング
もう1つの重要な最適化コンポーネントは、Frustumカリングです。可視性のピラミッドは、カメラが「見る」シーンの領域です。構築方法 まず、ポイントは4つの座標系(ローカル、ワールド、ビュー、投影の各座標系)にある可能性があることに注意してください。それらの間の遷移は、マトリックス、世界、種、および投影マトリックスによって実行され、変換は、ローカルから世界、世界から種、そして最後に種から投影空間に順番に行われなければなりません。これらの行列を乗算することにより、これらのすべての変換を1つにまとめることができます。透視投影法を使用します。これは、いわゆる「均一除算」を意味します。ベクトル(Px、Py、Pz、1)に投影行列を乗算した後、その成分をこのベクトルのW成分に分割します。投影空間への移行と均一な分割の後、ポイントはNDC空間に表示されます。NDC空間は3つの座標x、y、zのセットです。xとyは[-1、1]に属し、zは[0,1]に属します(OpenGLではパラメーターが多少異なると言わなければなりません)。それでは、問題の解決に取りかかりましょう。私の場合、ピラミッドはビューポートにあります。それを記述する6つの平面が必要です(図17a)。平面は、法線とこの平面に属する点を使用して記述できます。まず、ポイントを取得しましょう-これのために、NDC空間で次の座標セットを取得します。 std::vector<Point4F> pointsN = { {-1.0f, -1.0f, 0.0f, 1.0f}, {-1.0f, 1.0f, 0.0f, 1.0f}, { 1.0f, 1.0f, 0.0f, 1.0f}, {1.0f, -1.0f, 0.0f, 1.0f}, {-1.0f, -1.0f, 1.0f, 1.0f}, {-1.0f, 1.0f, 1.0f, 1.0f}, { 1.0f, 1.0f, 1.0f, 1.0f}, {1.0f, -1.0f, 1.0f, 1.0f} };
最初の4点でzの値は0です-これは、それらが近いクリッピング平面に属し、最後の4点でzが1-それらが遠いクリッピング平面に属することを意味します。次に、これらのポイントをビューポートに変換する必要があります。しかし、どのように?宇宙飛行士についての例を覚えておいてください-そして、これは同じことです。点に逆投影行列を掛ける必要があります。確かに、この後、それぞれを座標Wで割る必要があります。その結果、必要な座標を取得します(図17b)。ここで、法線を扱いましょう-それらはピラミッド内に向けられるべきなので、ベクトル積の計算に必要な順序を選択する必要があります。 Matrix4x4 invProj = Matrix4x4::Inverse(camera->GetProjMatrix()); std::vector<Point3F> pointsV; for(const Point4F &pN : pointsN){ Point4F pV = invProj.Transform(pN); pV /= pV.w; pointsV.push_back(Cast<Point3F>(pV)); } planes[0] = {pointsV[0], pointsV[1], pointsV[2]};
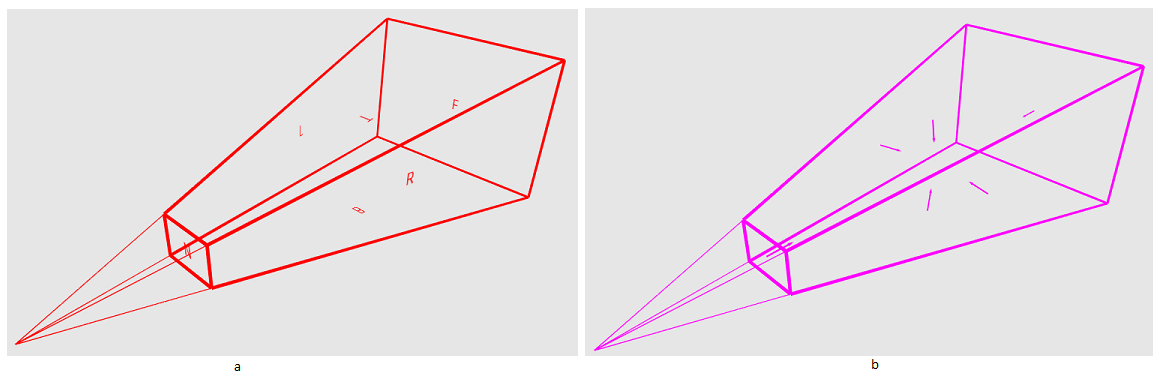 図17可視性のピラミッドピラミッドは構築されています-使用する時が来ました。ピラミッド内に収まらないセクターは描画しません。セクターが可視性のピラミッド内にあるかどうかを判断するために、このセクターの中心にある境界球を確認します。これでは正確な結果は得られませんが、この場合、いくつかの余分なセクターが描画されるという事実に問題はありません。球の半径は次のように計算されます。
図17可視性のピラミッドピラミッドは構築されています-使用する時が来ました。ピラミッド内に収まらないセクターは描画しません。セクターが可視性のピラミッド内にあるかどうかを判断するために、このセクターの中心にある境界球を確認します。これでは正確な結果は得られませんが、この場合、いくつかの余分なセクターが描画されるという事実に問題はありません。球の半径は次のように計算されます。 ここで、TRはセクターの右上隅、BLは左下隅です。すべてのセクターは同じ面積を持っているため、半径を一度計算すれば十分です。セクターを記述する球体が可視性ピラミッド内にあるかどうかをどのように判断しますか?まず、球体が平面と交差するかどうかを判断する必要があります。そうでない場合は、球体のどちら側からであるかを判断します。球の中心にあるベクトルを取得しましょう
ここで、TRはセクターの右上隅、BLは左下隅です。すべてのセクターは同じ面積を持っているため、半径を一度計算すれば十分です。セクターを記述する球体が可視性ピラミッド内にあるかどうかをどのように判断しますか?まず、球体が平面と交差するかどうかを判断する必要があります。そうでない場合は、球体のどちら側からであるかを判断します。球の中心にあるベクトルを取得しましょう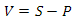 ここで、Pは平面上の点、Sは球の中心です。次に、法線平面でこのベクトルのスカラー積を計算します。方向は、スカラー積の符号を使用して決定できます。前述のように、正の場合、球は平面の前にあり、負の場合、球は後ろにあります。球が平面と交差するかどうかを判断するために残っています。 N(法線ベクトル)とVの2つのベクトルを取りましょう。NからVへのベクトルを作成しましょう。Kと呼びましょう。したがって、Kと正式に90度の角度を形成するような長さNを見つける必要があります。 Kは直交していました)。さてドック、図18aを見てください-直角三角形のプロパティから
ここで、Pは平面上の点、Sは球の中心です。次に、法線平面でこのベクトルのスカラー積を計算します。方向は、スカラー積の符号を使用して決定できます。前述のように、正の場合、球は平面の前にあり、負の場合、球は後ろにあります。球が平面と交差するかどうかを判断するために残っています。 N(法線ベクトル)とVの2つのベクトルを取りましょう。NからVへのベクトルを作成しましょう。Kと呼びましょう。したがって、Kと正式に90度の角度を形成するような長さNを見つける必要があります。 Kは直交していました)。さてドック、図18aを見てください-直角三角形のプロパティから 、コサインを見つける必要があることがわかります。前述のスカラー積プロパティを使用して、
、コサインを見つける必要があることがわかります。前述のスカラー積プロパティを使用して、 両側を| V | * | N |で除算します。そして得る
両側を| V | * | N |で除算します。そして得る この結果を使用します:
この結果を使用します: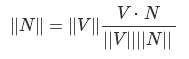 から| V | V | |それは上のカットバックすることが可能で、ちょうど数だし、我々が得る
から| V | V | |それは上のカットバックすることが可能で、ちょうど数だし、我々が得る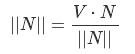 ベクトルNが正規化されているので、結果の値によって、我々は単に乗算それ最後のステップを、それ以外のベクトルが正規化されなければならない-この場合には、このような最終方程式ルックス:
ベクトルNが正規化されているので、結果の値によって、我々は単に乗算それ最後のステップを、それ以外のベクトルが正規化されなければならない-この場合には、このような最終方程式ルックス: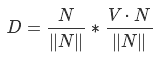 どこでDこれが新しいベクターです。このプロセスは「ベクトル投影」と呼ばれます(図18b)。しかし、なぜこれが必要なのでしょうか?我々は、ベクトルの長さと方向によって決定され、その位置から変化しないことを知っている-我々はそれがSを指摘するようにDを配置する場合、その長さは、平面(ris.18s)へSから最小距離に等しいことは、この手段を
どこでDこれが新しいベクターです。このプロセスは「ベクトル投影」と呼ばれます(図18b)。しかし、なぜこれが必要なのでしょうか?我々は、ベクトルの長さと方向によって決定され、その位置から変化しないことを知っている-我々はそれがSを指摘するようにDを配置する場合、その長さは、平面(ris.18s)へSから最小距離に等しいことは、この手段を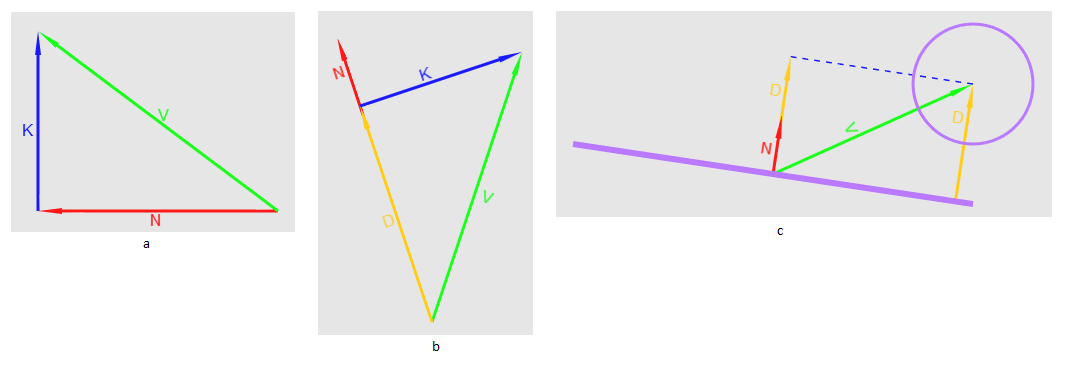 図.18 a NのVへの投影、bポイントに適用される投影Nの長さの視覚的表現、s視覚的表現
図.18 a NのVへの投影、bポイントに適用される投影Nの長さの視覚的表現、s視覚的表現
Sを中心とする球に適用される投影Nの長さ投影ベクトルは必要ないので、長さを計算するだけで十分です。 Nが単位ベクトルである場合、Vのスカラー積をNだけで計算する必要があります。すべてをまとめると、球の中心と平面の法線とのベクトルのスカラー積の値がゼロより大きく半径より小さい場合、球は最終的に平面と交差すると結論付けることができますこの球。球体が可視性のピラミッドの内側にあると主張するためには、それが平面の1つと交差するか、各平面の前にあることを確認する必要があります。友だちに質問することができます-球体が交差せず、少なくとも1つの飛行機の背後にある場合、それは間違いなく可視性のピラミッドの外側にあります。だからやる。球体の中心を、ピラミッドが配置されているのと同じ空間、つまりビューの空間に変換することに注意してください。 bool Frustum::TestSphere(const Point3F &Pos, float Radius, const Matrix4x4 &WorldViewMatrix) const { Point3F posV = WorldViewMatrix.Transform(Pos); for(const Plane &pl : planes){ Vector3 toSphPos = posV - pl.pos; if(Vector3::Dot(toSphPos, pl.normal) < -Radius) return false; } return true; }
10.クラック
解決しなければならないもう1つの問題は、詳細レベルの境界での亀裂です(図19)。 図19景観亀裂のデモンストレーションまず、詳細レベルの境界にあるセクターを特定する必要があります。一見、これはリソース集約型のタスクのようです-各レベルのセクターの数は絶えず変化しているためです。ただし、隣接データを使用する場合、ソリューションは大幅に簡素化されます。隣接データとは何ですか?各セクターには4つの近隣があります。それらへの参照のセット-ポインターまたはインデックス-隣接データです。彼らの助けを借りて、どのセクターが国境にあるかを簡単に判断できます-隣人がどのレベルに属しているかを確認するだけです。さて、各セクターの隣人を見つけましょう。繰り返しますが、すべてのセクターをループする必要はありません。グリッド空間のX座標とY座標を持つセクターで作業していると想像してください。立方体の端に触れない場合、その隣の座標は次のようになります:上からの隣人-(X、Y-1)下からの隣人-(X、Y + 1)左からの隣人-(X-1、Y)右からの隣人-(X + 1、Y)セクターがrib骨に触れる場合、その特別な容器を入れます。6つの面すべてを処理した後、キューブのすべての境界セクターが含まれます。このコンテナでは、整理する必要があります。事前に、各セクターのエッジを計算します。
図19景観亀裂のデモンストレーションまず、詳細レベルの境界にあるセクターを特定する必要があります。一見、これはリソース集約型のタスクのようです-各レベルのセクターの数は絶えず変化しているためです。ただし、隣接データを使用する場合、ソリューションは大幅に簡素化されます。隣接データとは何ですか?各セクターには4つの近隣があります。それらへの参照のセット-ポインターまたはインデックス-隣接データです。彼らの助けを借りて、どのセクターが国境にあるかを簡単に判断できます-隣人がどのレベルに属しているかを確認するだけです。さて、各セクターの隣人を見つけましょう。繰り返しますが、すべてのセクターをループする必要はありません。グリッド空間のX座標とY座標を持つセクターで作業していると想像してください。立方体の端に触れない場合、その隣の座標は次のようになります:上からの隣人-(X、Y-1)下からの隣人-(X、Y + 1)左からの隣人-(X-1、Y)右からの隣人-(X + 1、Y)セクターがrib骨に触れる場合、その特別な容器を入れます。6つの面すべてを処理した後、キューブのすべての境界セクターが含まれます。このコンテナでは、整理する必要があります。事前に、各セクターのエッジを計算します。 struct SectorEdges { CubeSectors::Sector *owner; typedef std::pair<Point3F, Point3F> Edge; Edge edges[4]; }; std::vector<SectorEdges> sectorsEdges;
次はバストそのものです for(SectorEdges &edgs : sectorsEdges) for(size_t e = 0; e < 4; e++) if(edgs.owner->adjacency[e] == nullptr) FindSectorEdgeAdjacency(edgs, (AdjacencySide)e, sectorsEdges);
FindSectorEdgeAdjacency()関数は次のようになります void CubeSectors::FindSectorEdgeAdjacency(SectorEdges &Sector, CubeSectors::AdjacencySide Side, std::vector<SectorEdges> &Neibs) { SectorEdges::Edge &e = Sector.edges[Side]; for(SectorEdges &edgs2 : Neibs){ if(edgs2.owner == Sector.owner) continue; for(size_t e = 0; e < 4; e++){ SectorEdges::Edge &e2 = edgs2.edges[e]; if((Math::Equals(e.first, e2.first) && Math::Equals(e.second, e2.second)) || (Math::Equals(e.second, e2.first) && Math::Equals(e.first, e2.second))) { Sector.owner->adjacency[Side] = edgs2.owner; edgs2.owner->adjacency[e] = Sector.owner; return; } } } }
2つのセクターの隣接データを更新することに注意してください-目的の(セクター)と見つかった隣接。次に、隣接データを使用して、詳細レベルの境界に属するセクターのエッジを見つける必要があります。そのような計画-レンダリングする前に、境界セクターを見つけます。次に、各セクターのインスタンスバッファーに、主な情報に加えて、隣接セクターのテッセレーション係数とテッセレーション係数の4次元ベクトルを書き込みます。頂点の説明は次のようになります。 std::vector<D3D11_INPUT_ELEMENT_DESC> meta = {
詳細レベルでセクターを割り当てた後、各セクターの隣接テッセレーション係数を決定します。 for(LodsStorage::Lod &lod : lods){ const std::vector<Sector*> §ors = lod.GetSectors(); bool lastLod = lod.GetInd() == lods.GetCount() - 1; for(Sector *s : sectors){ int32_t tessFacor = s->GetTessFactor(); s->GetBorderTessFactor() = { GetNeibTessFactor(s, Sector::ADJ_BOTTOM, tessFacor, lastLod), GetNeibTessFactor(s, Sector::ADJ_LEFT, tessFacor, lastLod), GetNeibTessFactor(s, Sector::ADJ_TOP, tessFacor, lastLod), GetNeibTessFactor(s, Sector::ADJ_RIGHT, tessFacor, lastLod) }; } }
隣接するテッセレーション係数を検索する関数: float Terrain::GetNeibTessFactor(Sector *Sec, Sector::AdjacencySide Side, int32_t TessFactor, bool IsLastLod) { Sector *neib = Sec->GetAdjacency()[Side]; int32_t neibTessFactor = neib->GetTessFactor(); return (neibTessFactor < TessFactor) ? (float)neibTessFactor : 0.0f; }
ゼロを返す場合、サイド側の隣人は私たちにとって関心がありません。先に進み、テッセレーション係数が大きいレベルの側面から亀裂を除去する必要があると言います。シェーダーに渡しましょう。まず、テッセレータの座標を使用してグリッド座標を取得する必要があることを思い出させてください。次に、これらの座標が立方体の端の点に変換され、この点が正規化されます-これで、球上の点ができました。 float3 p = Tri[0].netPos * Coord.x + Tri[1].netPos * Coord.y + Tri[2].netPos * Coord.z; float3 planePos = Tri[0].startPos + Tri[0].vec1 * px * gridStep.x + Tri[0].vec2 * py * gridStep.y; float3 sphPos = normalize(planePos);
まず、頂点がグリッドの最初または最後の行に属しているか、最初または最後の列に属しているかを調べる必要があります。この場合、頂点はセクターの端に属します。しかし、これでは十分ではありません。頂点が詳細レベルの境界に属しているかどうかを判断する必要があります。これを行うために、隣接セクターに関する情報、またはむしろそれらのテセレーションレベルを使用します。 float4 bTf = Tri[0].borderTessFactor; bool isEdge = (bTf.x != 0.0f && py == 0.0f) ||
現在、主な段階は実際には亀裂の除去です。図20をご覧ください。赤い線は、2番目の詳細レベルに属するピークのエッジです。 2本の青い線-3番目の詳細レベルの境界。 V3は赤い線に属している必要があります-つまり、第2レベルの危機にonしています。高さV1とV2は両方のレベルで等しいため、V3はそれらの間の線形補間によって見つけることができます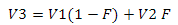
 図20線の形で亀裂を形成する面のデモンストレーションこれまでのところ、V1とV2も係数Fもありません。まず、ポイントV3のインデックスを見つける必要があります。つまり、グリッドのサイズが32 x 32で、テッセレーション係数が4の場合、このインデックスは0〜128(32 * 4)になります。グリッド空間pにはすでに座標があります-この例のフレームワークでは、たとえば(15.5、16)になります。インデックスを取得するには、座標pの1つにテッセレーション係数を乗算します。また、顔の始まりとその終わりへの方向、つまりセクターのコーナーの1つも必要です。
図20線の形で亀裂を形成する面のデモンストレーションこれまでのところ、V1とV2も係数Fもありません。まず、ポイントV3のインデックスを見つける必要があります。つまり、グリッドのサイズが32 x 32で、テッセレーション係数が4の場合、このインデックスは0〜128(32 * 4)になります。グリッド空間pにはすでに座標があります-この例のフレームワークでは、たとえば(15.5、16)になります。インデックスを取得するには、座標pの1つにテッセレーション係数を乗算します。また、顔の始まりとその終わりへの方向、つまりセクターのコーナーの1つも必要です。 float edgeVertInd = 0.0f; float3 edgeVec = float3(0.0f, 0.0f, 0.0f); float3 startPos = float3(0.0f, 0.0f, 0.0f); uint neibTessFactor = 0; if(bTf.x != 0.0f && py == 0.0f){
次に、V1とV2のインデックスを見つける必要があります。数字の3があるとします。2の倍数である2つの最も近い数字を見つける必要があります。これを行うには、3を2で割った余りを計算します(1に等しい)。次に、この剰余を3に減算または加算して、目的の結果を取得します。また、インデックスでは、2つではなく、詳細レベルのテッセレーション係数の比率があります。つまり、3番目のレベルの係数が16で、2番目のレベル2の係数が8の場合、比率は8になります。ここで、高さを取得するには、まず球の対応するポイントを取得し、エッジのポイントを正規化する必要があります。リブの始点と方向はすでに準備されています。V1からV2までのベクトルの長さを計算することは残っています。元のメッシュセルのエッジの長さはgridStep.xであるため、必要な長さはgridStep.x / Tri [0] .tessFactorです。次に、前述のように、球体のポイントで高さを取得します。 float GetNeibHeight(float3 EdgeStartPos, float3 EdgeVec, float VecLen, float3 NormOffset) { float3 neibPos = EdgeStartPos + EdgeVec * VecLen; neibPos = normalize(neibPos); return GetHeight(neibPos, NormOffset); } float vertOffset = gridStep.x / Tri[0].tessFactor; uint tessRatio = (uint)tessFactor / (uint)neibTessFactor; uint ind = (uint)edgeVertInd % tessRatio; uint leftNeibInd = (uint)edgeVertInd - ind; float leftNeibHeight = GetNeibHeight(startPos, edgeVec, vertOffset * leftNeibInd, normOffset); uint rightNeibInd = (uint)edgeVertInd + ind; float rightNeibHeight = GetNeibHeight(startPos, edgeVec, vertOffset * rightNeibInd, normOffset);
さて、最新のコンポーネントは係数Fです。除算の残りを係数の比(ind)で除算し、係数の比(tessRatio)で除算することで得られます。 float factor = (float)ind / (float)tessRatio;
最終段階-高さの線形補間と新しい頂点の取得 float avgHeight = lerp(leftNeibHeight, rightNeibHeight, factor); posL = sphPos * (sphereRadius + avgHeight);
セクターの境界が1または0に等しいエッジのテクスチャ座標にある場所にも亀裂が発生する場合があります。この場合、2つの座標の高さの平均値を取得します。 float GetHeight(float2 TexCoords) { float2 texCoords2 = TexCoords * texCoordsScale; float mHeight = mainHeightTex.SampleLevel(mainHeightTexSampler, TexCoords, 0).x; float dHeight = distHeightTex.SampleLevel(distHeightTexSampler, texCoords2, 0).x; return (mHeight + dHeight) * maxTerrainHeight; } float GetHeight(float3 SphPos, float3 NormOffset) { float2 texCoords1 = GetTexCoords(SphPos, NormOffset); float height = GetHeight(texCoords1); if(texCoords1.x == 1.0f){ float height2 = GetHeight(float2(0.0f, texCoords1.y)); return lerp(height, height2, 0.5f); }else if(texCoords1.x == 0.0f){ float height2 = GetHeight(float2(1.0f, texCoords1.y)); return lerp(height, height2, 0.5f); }else return height; }
11. GPUでの処理
セクターの処理をGPUに転送しましょう。 2つのコンピュートシェーダーがあります。1つ目は可視性ピラミッドを切り取り、詳細レベルを決定し、2つ目は境界テッセレーション係数を受け取ってクラックを除去します。 CPUの場合のように、切断するまでセクターの隣接を正しく判断できないため、2段階に分ける必要があります。両方のシェーダーは詳細レベルのデータを使用し、セクターを処理するため、セクターとロッドの2つの一般的な構造を導入しました。 struct Sector { float3 vec1, vec2; float3 startPos; float3 normCenter; int adjacency[4]; float borderTessFactor[4]; int lod; }; struct Lod { RangeF dotRange; float tessFactor; float padding; float4 color; };
入力(セクターに関する初期情報を含む)、中間(最初の段階の結果として取得されたセクターのデータを含む)、最終(レンダリングに転送されます)の3つのメインバッファーを使用します。入力バッファーのデータは変更されないため、D3D11_BUFFER_DESC構造体のUsageフィールドに値D3D11_USAGE_IMMUTABLEを使用するのが合理的です。すべてのセクターのデータを書き込むだけで、隣接データにはセクターポインターではなくセクターインデックスを使用します。詳細レベルのインデックスとテッセレーションの境界係数には、ゼロ値を設定します。 static const size_t sectorSize = sizeof(Vector3) +
次に、中間バッファについて少し説明します。最初のシェーダーの出力と2番目のシェーダーの入力という2つの役割を果たします。したがって、BindFlagsフィールドをD3D11_BIND_UNORDERED_ACCESSに設定します。D3D11_BIND_SHADER_RESOURCE。また、シェーダーが作業結果を書き込むことができるUnorderedAccessViewと、バッファーを入力として使用するShaderResourceViewの2つのディスプレイを作成します。そのサイズは、以前に作成された入力バッファと同じになります UINT miscFlags = D3D11_BIND_UNORDERED_ACCESS | D3D11_BIND_SHADER_RESOURCE; intermediateData = Utils::DirectX::CreateBuffer( sectors.GetSectors().size() * sectorSize,
次に、最初のシェーダーの主な機能を示します。 StructuredBuffer<Sector> inputData : register(t0); RWStructuredBuffer<Sector> outputData : register(u0); [numthreads(1, 1, 1)] void Process( int3 TId : SV_DispatchThreadID ) { int ind = TId.x; Sector sector = inputData[ind]; float dotVal = dot(toWorldPos, sector.normCenter); if(dotVal < dotRange.minVal || dotVal > dotRange.maxVal){ outputData[ind] = sector; return; } if(!IsVisible(sector.normCenter)){ outputData[ind] = sector; return; } for(int l = 0; l < 4; l++){ Lod lod = lods[l]; if(dotVal >= lod.dotRange.minVal && dotVal <= lod.dotRange.maxVal) sector.lod = l + 1; } outputData[ind] = sector; }
スカラー積を計算した後、セクターが潜在的に見える領域にあるかどうかを確認します。次に、前に示したFrustum :: TestSphere()呼び出しと同一のIsVisible()呼び出しを使用して、その可視性の事実を明確にします。関数の操作は、変数worldView、sphereRadius、frustumPlanesPosV、およびfrustumPlanesNormalsVに依存します。これらの値は、事前にシェーダーに渡す必要があります。次に、詳細レベルを決定します。単一からのレベルインデックスを示していることに注意してください。これは、第2段階で詳細レベルがゼロのセクターを破棄するために必要です。次に、第2段階のバッファーを準備する必要があります。 Computeシェーダーの出力とテッセレーターの入力としてバッファーを使用します-このため、BindFlagsフィールドで値D3D11_BIND_UNORDERED_ACCESSを指定する必要があります| D3D11_BIND_VERTEX_BUFFER。バッファデータを直接操作する必要があるため、MiscFlagsフィールドに値D3D11_RESOURCE_MISC_BUFFER_ALLOW_RAW_VIEWSを指定します。このようなバッファを表示するには、FlagsフィールドにDXGI_FORMAT_R32_TYPELESS値を使用し、NumElementsフィールドに4つのバッファすべてを示します size_t instancesByteSize = instanceByteSize * sectors.GetSectors().size(); outputData = Utils::DirectX::CreateBuffer(instancesByteSize, D3D11_BIND_UNORDERED_ACCESS | D3D11_BIND_VERTEX_BUFFER, D3D11_USAGE_DEFAULT, 0, D3D11_RESOURCE_MISC_BUFFER_ALLOW_RAW_VIEWS, 0); D3D11_BUFFER_UAV uavParams = {0, instancesByteSize / 4, D3D11_BUFFER_UAV_FLAG_RAW}; outputUAW = Utils::DirectX::CreateUnorderedAccessView(outputData, uavParams, DXGI_FORMAT_R32_TYPELESS);
カウンターも必要になります。これを使用して、シェーダーのメモリをアドレス指定し、DrawIndexedInstanced()呼び出しのinstanceCount引数でその最終値を使用します。カウンターをサイズが16バイトのバッファーとして実装しました。また、D3D11_BUFFER_UAVフィールドのFlagsフィールドに表示を作成するときに、値D3D11_BUFFER_UAV_FLAG_COUNTERを使用しました counter = Utils::DirectX::CreateBuffer(sizeof(UINT), D3D11_BIND_UNORDERED_ACCESS, D3D11_USAGE_DEFAULT, 0, D3D11_RESOURCE_MISC_BUFFER_STRUCTURED, 4); D3D11_BUFFER_UAV uavParams = {0, 1, D3D11_BUFFER_UAV_FLAG_COUNTER}; counterUAW = Utils::DirectX::CreateUnorderedAccessView(counter, uavParams);
2番目のシェーダーコードを使用します StructuredBuffer<Sector> inputData : register(t0); RWByteAddressBuffer outputData : register(u0); RWStructuredBuffer<uint> counter : register(u1); [numthreads(1, 1, 1)] void Process( int3 TId : SV_DispatchThreadID ) { int ind = TId.x; Sector sector = inputData[ind]; if(sector.lod != 0){ sector.borderTessFactor[0] = GetNeibTessFactor(sector, 0);
GetNeibTessFactor()関数のコードは、対応するCPUとほぼ同じです。唯一の違いは、近隣へのポインタではなく近隣のインデックスを使用することです。outputDataバッファーはRWByteAddressBuffer型であるため、Storeメソッド(uintアドレス、uint値)を使用して操作します。dataSize変数の値は、D3D11_INPUT_PER_INSTANCE_DATAクラスの頂点データのサイズと等しく、頂点の説明はセクション10にあります。一般に、これはC / C ++のポインターを使用した従来の作業です。2つのシェーダーを実行した後、outputDataをInstanceBufferとして使用できます。レンダリングプロセスは次のようになります Utils::DirectX::SetPrimitiveStream({vb, outputData}, ib, {vertexSize, instanceByteSize}, D3D11_PRIMITIVE_TOPOLOGY_3_CONTROL_POINT_PATCHLIST); DeviceKeeper::GetDeviceContext()->CopyStructureCount(indirectArgs, 4, counterUAW); Shaders::Apply(terrainShaders, [&]() { DeviceKeeper::GetDeviceContext()->DrawIndexedInstancedIndirect(indirectArgs, 0); }); Utils::DirectX::SetPrimitiveStream({nullptr, nullptr}, nullptr, {0, 0});
DrawIndexedInstancedIndirect()およびCopyStructureCount()メソッドの詳細については、付録2を参照してください。12.カメラ
簡単なFPS(ファーストパーソンシューター)カメラをモデル化する方法はご存じでしょう。私はこのシナリオに従って行動します:- 1. 2つの角度から方向ベクトルを取得します
- 2.方向ベクトルとベクトル(0、1、0)を使用して、基底を取得します
- 3.手順2で取得した方向ベクトルと右のベクトルに従って、カメラの位置を変更します
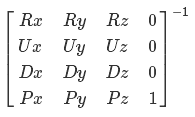 私たちの場合、状況はやや複雑です-最初に、惑星の中心に対して移動する必要があり、2番目に、ベクトル(0、1、0)の代わりに基底を構築するときに、現在の点で球の法線を使用する必要があります。望ましい結果を達成するために、2つのベースを使用します。前者によれば、位置が変わり、後者はカメラの向きを説明します。基底は相互依存していますが、最初に位置の基底を計算するため、それから始めます。初期位置ベース(pDir、pUp、pRight)と、距離を移動する方向ベクトルvDirがあるとします。まず、vDirの投影をpDirおよびpRightで計算する必要があります。それらを追加すると、更新された方向ベクトルが得られます(図21)。
私たちの場合、状況はやや複雑です-最初に、惑星の中心に対して移動する必要があり、2番目に、ベクトル(0、1、0)の代わりに基底を構築するときに、現在の点で球の法線を使用する必要があります。望ましい結果を達成するために、2つのベースを使用します。前者によれば、位置が変わり、後者はカメラの向きを説明します。基底は相互依存していますが、最初に位置の基底を計算するため、それから始めます。初期位置ベース(pDir、pUp、pRight)と、距離を移動する方向ベクトルvDirがあるとします。まず、vDirの投影をpDirおよびpRightで計算する必要があります。それらを追加すると、更新された方向ベクトルが得られます(図21)。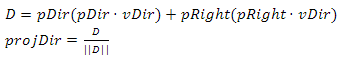
 図21 projDirを取得するための視覚的なプロセス次に、このベクトル
図21 projDirを取得するための視覚的なプロセス次に、このベクトル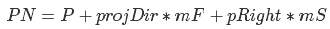 に沿って移動します。Pはカメラの位置、mFとmSは係数です。これは、前方または側方に移動する必要がある量を意味します。PNは球体に属さないため、PNを新しいカメラ位置として使用することはできません。代わりに、ポイントPNで球の法線を見つけ、この法線はベクトルupの新しい値になります。今、私たちは更新された基礎を形成することができます
に沿って移動します。Pはカメラの位置、mFとmSは係数です。これは、前方または側方に移動する必要がある量を意味します。PNは球体に属さないため、PNを新しいカメラ位置として使用することはできません。代わりに、ポイントPNで球の法線を見つけ、この法線はベクトルupの新しい値になります。今、私たちは更新された基礎を形成することができます Vector3 nUp = Vector3::Normalize(PN - spherePos); Vector3 nDir = projDir Vector3 nRight = Vector3::Normalize(Vector3::Cross(pUp, pDir))
ここで、spherePosは球の中心です。各ベクトルを他の2つのベクトルに直交させる必要があります。ベクトル積の特性に従って、nRightはこの条件を満たします。 nUpとnDirで同じことを達成するために残っています。これを行うには、nDirをnUpに投影し、結果のベクトルをnDirから減算します(図22)。図22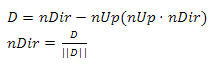
 nUpに対するnDirの直交化nUpでも同じことができますが、方向が変わるため、この場合は受け入れられません。次に、nDirを正規化し、方向の更新された正規直交基底を取得します。2番目の重要なステップは、オリエンテーションの基礎を構築することです。主な問題は、方向ベクトルを取得することです。最も適切な解決策は、極角a、方位角b、および原点からの距離が1に等しい点を球面座標からデカルト座標に変換することです。極角がゼロに等しいポイントに対してこのような遷移を行う場合にのみ、ベクトルが見上げられます。角度をインクリメントし、そのようなベクトルが前方を向くと仮定するため、これは私たちには完全に適していません。 90度の通常の角度シフトで問題は解決しますが、角度シフトルールを使用するとよりエレガントに
nUpに対するnDirの直交化nUpでも同じことができますが、方向が変わるため、この場合は受け入れられません。次に、nDirを正規化し、方向の更新された正規直交基底を取得します。2番目の重要なステップは、オリエンテーションの基礎を構築することです。主な問題は、方向ベクトルを取得することです。最も適切な解決策は、極角a、方位角b、および原点からの距離が1に等しい点を球面座標からデカルト座標に変換することです。極角がゼロに等しいポイントに対してこのような遷移を行う場合にのみ、ベクトルが見上げられます。角度をインクリメントし、そのようなベクトルが前方を向くと仮定するため、これは私たちには完全に適していません。 90度の通常の角度シフトで問題は解決しますが、角度シフトルールを使用するとよりエレガントに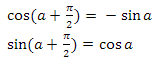 なります。その結果、次
なります。その結果、次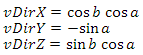 が得られます。ここで、aは極角、bは方位角です。この結果は、私たちに完全に適しているわけではありません-位置に基づいて方向ベクトルを構築する必要があります。 vDirの方程式を書き直しましょう。
が得られます。ここで、aは極角、bは方位角です。この結果は、私たちに完全に適しているわけではありません-位置に基づいて方向ベクトルを構築する必要があります。 vDirの方程式を書き直しましょう。 宇宙飛行士のようなものはすべて、この方向に非常に多く、その方向に非常に多くのものを持っています。ここで、標準基底のベクトルをpDir、pUp、およびpRightに置き換えると、必要な方向が得られることは明らかです。
宇宙飛行士のようなものはすべて、この方向に非常に多く、その方向に非常に多くのものを持っています。ここで、標準基底のベクトルをpDir、pUp、およびpRightに置き換えると、必要な方向が得られることは明らかです。このように
 同じことを行列乗算の形で想像できますが、
同じことを行列乗算の形で想像できますが、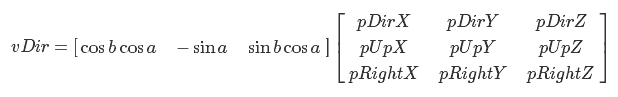 ベクトルvUpは最初はpUpと等しくなります。 vUpとvDirのベクトル積を計算することでvRightを取得し、vUpを
ベクトルvUpは最初はpUpと等しくなります。 vUpとvDirのベクトル積を計算することでvRightを取得し、vUpを 残りの基底ベクトルに直交させます。原理はnDirを使用するときと同じで
残りの基底ベクトルに直交させます。原理はnDirを使用するときと同じで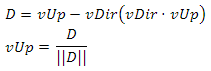 、ベースを見つけました-カメラの位置を計算するために残っています。これは
、ベースを見つけました-カメラの位置を計算するために残っています。これは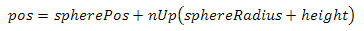 、spherePosが球体の中心、sphereRadiusが球体の半径、heightが球体の表面からの高さである場合に行われます。説明したカメラのコードを示します。
、spherePosが球体の中心、sphereRadiusが球体の半径、heightが球体の表面からの高さである場合に行われます。説明したカメラのコードを示します。 float moveFactor = 0.0f, sideFactor = 0.0f, heightFactor = 0.0f; DirectInput::GetInsance()->ProcessKeyboardDown({ {DIK_W, [&](){moveFactor = 1.0f;}}, {DIK_S, [&](){moveFactor = -1.0f;}}, {DIK_D, [&](){sideFactor = 1.0f;}}, {DIK_A, [&](){sideFactor = -1.0f;}}, {DIK_Q, [&](){heightFactor = 1.0f;}}, {DIK_E, [&](){heightFactor = -1.0f;}} }); if(moveFactor != 0.0f || sideFactor != 0.0f){ Vector3 newDir = Vector3::Normalize(pDir * Vector3::Dot(pDir, vDir) + pRight * Vector3::Dot(pRight, vDir)); Point3F newPos = pos + (newDir * moveFactor + pRight * sideFactor) * Tf * speed; pDir = newDir; pUp = Vector3::Normalize(newPos - spherePos); pRight = Vector3::Normalize(Vector3::Cross(pUp, pDir)); pDir = Vector3::Normalize(pDir - pUp * Vector3::Dot(pUp, pDir)); pos = spherePos + pUp * (sphereRadius + height); angles.x = 0.0f; } if(heightFactor != 0.0f){ height = Math::Saturate(height + heightFactor * Tf * speed, heightRange); pos = spherePos + pUp * (sphereRadius + height); } DirectInput::MouseState mState = DirectInput::GetInsance()->GetMouseDelta(); if(mState.x != 0 || mState.y != 0 || moveFactor != 0.0f || sideFactor != 0.0f){ if(mState.x != 0) angles.x = angles.x + mState.x / 80.0f; if(mState.y != 0) angles.y = Math::Saturate(angles.y + mState.y / 80.0f, RangeF(-Pi * 0.499f, Pi * 0.499f)); vDir = Vector3::Normalize(pRight * sinf(angles.x) * cosf(angles.y) + pUp * -sinf(angles.y) + pDir * cosf(angles.x) * cosf(angles.y)); vUp = pUp; vRight = Vector3::Normalize(Vector3::Cross(vUp, vDir)); vUp = Vector3::Normalize(vUp - vDir * Vector3::Dot(vDir, vUp)); } viewMatrix = Matrix4x4::Inverse({{vRight, 0.0f}, {vUp, 0.0f}, {vDir, 0.0f}, {pos, 1.0f}});
位置の基準を更新した後、angles.xをゼロにすることに注意してください。これは重要です。視野角を同時に変更し、球体の周りを移動することを想像してみましょう。まず、方向ベクトルをpDirとpRightに投影し、オフセット(newPos)を取得して、それに基づいて位置の基底を更新します。2番目の条件も機能し、オリエンテーションベースの更新を開始します。しかし、pDirとpRightはvDirに応じてすでに変更されているため、方位角(angles.x)をリセットせずに、回転はより「クール」になります。おわりに
読者が記事に興味を持ってくれたことに感謝します。その中に含まれている情報が彼にとって利用可能であり、興味深く有用であったことを願っています。あなたは私に電子メールalexwin32@mail.ruで提案やコメントを送るか、コメントの形で私を残すことができます。成功を祈っています!付録1InstanceDataStepRate , D3D11_INPUT_PER_VERTEX_DATA D3D11_INPUT_PER_INSTANCE_DATA. — . « ?» — . . — , 99 . :
UINT colorsRate = 99 / 3; std::vector<D3D11_INPUT_ELEMENT_DESC> meta = { {"POSITION", 0, DXGI_FORMAT_R32G32B32_FLOAT, 0, 0, D3D11_INPUT_PER_VERTEX_DATA, 0}, {"NORMAL", 0, DXGI_FORMAT_R32G32B32_FLOAT, 0, 12, D3D11_INPUT_PER_VERTEX_DATA, 0}, {"TEXCOORD", 0, DXGI_FORMAT_R32G32_FLOAT, 0, 24, D3D11_INPUT_PER_VERTEX_DATA, 0}, {"WORLD", 0, DXGI_FORMAT_R32G32B32A32_FLOAT, 1, 0, D3D11_INPUT_PER_INSTANCE_DATA, 1}, {"WORLD", 1, DXGI_FORMAT_R32G32B32A32_FLOAT, 1, 16, D3D11_INPUT_PER_INSTANCE_DATA, 1}, {"WORLD", 2, DXGI_FORMAT_R32G32B32A32_FLOAT, 1, 32, D3D11_INPUT_PER_INSTANCE_DATA, 1}, {"WORLD", 3, DXGI_FORMAT_R32G32B32A32_FLOAT, 1, 48, D3D11_INPUT_PER_INSTANCE_DATA, 1}, {"COLOR", 0, DXGI_FORMAT_R32G32B32A32_FLOAT, 2, 0, D3D11_INPUT_PER_INSTANCE_DATA, colorsRate}, };
, , 33 «». 33 , 33 — .. . , , c D3D11_USAGE_IMMUTABLE. , , GPU , . :
matricesTb = Utils::DirectX::CreateBuffer(sizeof(Matrix4x4) * 99, D3D11_BIND_VERTEX_BUFFER, D3D11_USAGE_DYNAMIC, D3D11_CPU_ACCESS_WRITE); colorsTb = Utils::DirectX::CreateBuffer(colors, D3D11_BIND_VERTEX_BUFFER, D3D11_USAGE_IMMUTABLE, 0);
( — , )
Utils::DirectX::Map<Matrix4x4>(matricesTb, [&](Matrix4x4 *Data) {
,
付録2DrawIndexedInstanced() DrawIndexedInstancedIndirect() , , DrawIndexedInstanced(). D3D11_RESOURCE_MISC_DRAWINDIRECT_ARGS. :
, . これはどのように使用できますか? , GPU. — Compute AppendStructuredBuffer, . CopyStructureCount() «», DrawIndexedInstancedIndirect()
付録3, X a, z — Z :

. , . :
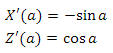
:

? . , ( t >= 0):
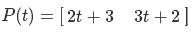
X

Y

, (2, 3),
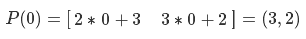
P(t) :

« (3, 2) t (2, 3)». :

X
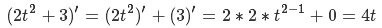
Y
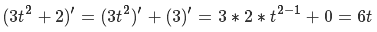
. : « (3, 2), ».