リードソロモンコード。 パート1-簡単な言語理論

こんにちは 私の名前はマキシムです。YADROでは、とりわけ、信頼性の高いデータストレージを担当するサブシステムを開発しています。 リードソロモンコードに関する短い記事シリーズを準備しています。理論的基礎、実用的な実装、および実用的なソフトウェアとハ​​ードウェアの最適化です。 Habréおよびその他のネットワークには、この分野の問題に関する優れた記事がありますが、トピックに慣れていない場合、それらを理解することは困難です。 この記事では、リードソロモンコードを明確に紹介し、次の号ではすべてのプログラミング方法を説明します。

リードソロモンコードを使用する理由

YADROの主要な作業分野の1つは、データストレージシステム（SHD）の開発です。 エンドユーザーの観点から、これらのシステムのどの特性が最も重要であるかを長い間議論できます。 これは、I / Oの速度、システムの所有コスト、エネルギー消費レベルなどです。 ただし、これらの特性はすべて、システムがユーザーが必要とするレベルのデータセキュリティを提供する場合にのみ意味を持ちます。 その結果、そのようなシステムのすべての開発者にとって、データストレージの信頼性を確保するという問題が前面に出てきます。

長い間、RAIDテクノロジーは安全なデータストレージの分野で主要なプレーヤーであり続けました。 このような従来のソリューションには、よく知られている利点とともに、特定の制限があります。 これらには以下が含まれます。

• 比較的低レベルの保護（たとえば、RAID 6は最大2台のドライブの障害をサポートします）
• スペアホイールを保管する必要がある
• 「パリティ」ブロックの分布を制御できない（これは特定のタイプのディスクにとって重要かもしれません）
• 「異種」ディスクのサポートの複雑さ

この点に関して、最近、あらゆる種類の冗長コードに基づく技術が人気を集めています（英語の文献では、このような技術には名前があります-消去符号化）。

現在、私たちのチームはTATLINストレージシステムを開発しています。 システムのアーキテクチャについては、別のシリーズの記事を書く予定です。ここでは、ある時点で、信頼できるデータストレージの独自のシステムを実装するという課題に直面したとのみ言います。 この問題を研究した後、私たちは長年の実績のあるリードソロモンコードについて詳しく調べることにしました。 事前に構築されたライブラリがあります（たとえば、IntelのISA-LやJames S. PlankのJerasureなど ）。 適切なエンコード/デコード手順を実装します。 しかし、ハードウェアプラットフォームがOpenPOWERアーキテクチャに基づいており、システムロジック全体がLinuxカーネルモジュールとして実装されていることを考慮して、システムの機能に合わせて実装を最適化することにしました。

この最初の記事では、ストレージシステムのコンテキストでリードソロモンコードについて話すときに、私たちが話していることを説明しようとします。 解決しようとしている問題の性質をよりよく理解するのに役立つ簡単な例から始めましょう。

失われたものを回復する基本的なタスク

2つの任意の整数があると仮定します $$$A$そして $$$B$。 3番目の数値とこれら2つの数値を一致させるアルゴリズムを開発する必要があります $$$R$、2つの初期番号のいずれかが失われると、それらのいずれかを明確に復元できるようになります。 つまり、ペア（ $$$A$そして $$$R$）または（ $$$B$そして $$$R$）、明確に復元することが可能です $$$B$または $$$A$それに応じて。 そのようなアルゴリズムを実装するための多くのオプションがありますが、おそらく最も簡単なのは、排他的OR（XOR）ビット操作を2つのソース番号に適用するものです。 $$$R = A xor B$。 その後、回復のために $$$A$平等を使用できます $$$A = R xor B$（リカバリー用 $$$B$、 $$$B = R xor A$）

タスクを少し複雑にしましょう。 開始番号が2つではなく、3つであるとします- $$$A$、 $$$B$そして $$$C$。 前と同様に、元の数値の1つが失われた場合に対処するアルゴリズムが必要です。 「Exclusive OR」ビット操作を再び使用することを妨げるものは何もないことに気付くのは簡単です。 $$$R = A xor B xor C$。 回復のために $$$A$平等を使用できます $$$A = R xor B xor C$。

タスクをもう少し複雑にしましょう。 前と同じように、3つの数字があります $$$A$、 $$$B$そして $$$C$しかし、失うために、今回は、1つではなく、2つのうちのいずれかです。 明らかに、排他的OR操作を使用するだけでは失敗します。 失われた番号を回復するには？

写真付きの簡単な例でのリードソロモンコーディングの原理

この問題を解決する方法の1つは、リードソロモンコードの使用です。 この方法の正式な説明はインターネット上で簡単に見つけることができますが、主な問題は、ガロア体から遠く離れた人々にとって、これが実際にどのように機能するかを理解するのが十分に難しいことです。 たとえば、 Wikipediaの定義は次のとおりです。



より直感的なことから始めて、それがどのように機能するかを理解してみましょう。 これを行うには、最後のタスクに戻ります。 3つの任意の整数があり、そのうちの2つが失われる可能性があることを思い出してください。残りから失われた数値を回復する方法を学ぶ必要があります。 これを行うには、「代数」アプローチを適用します。

しかし、最初に、もう1つの重要な点を思い出す必要があります。 データリカバリテクノロジーには、冗長コーディング方式と呼ばれる理由があります。 ソースデータによると、いくつかの「冗長な」データが計算され、失われたデータを回復できます。 詳細には触れませんが、データの損失量が多いほど、「冗長性」が必要になるというのが経験則です。 この場合、2つの数値を復元するには、何らかのアルゴリズムを使用して2つの「冗長な」数値を作成する必要があります。 一般的に、損失を維持する必要がある場合 $$$K$数字、あなたはそれに応じて持っている必要があります $$$K$過剰。

上記の「代数」アプローチは次のとおりです。 特別なタイプのサイズのマトリックスがコンパイルされます $$$5×3$。 この行列の最初の3行は単位行列を形成し、最後の2行はいくつかの数字です。これについては後で説明します。 英語の文学では、この行列は通常ジェネレータ行列と呼ばれ、ロシア語ではいくつかの名前があります;この記事では、生成行列が使用されます。 作成された行列に元の数字で構成されるベクトルを乗算します $$$A$、 $$$B$そして $$$C$。



行列にデータを含むベクトルを乗算した結果、図に示されているように、2つの「冗長」な数値が得られます。 $$$X_0$そして $$$X_1$。 この「冗長な」データの助けを借りて、たとえば失われたデータをどのように回復できるかを見てみましょう。 $$$A$そして $$$B$。

生成行列の「欠損」データに対応する線を消します。 私たちの場合 $$$A$最初の行に対応し、 $$$B$-2番目。 結果の行列にデータを含むベクトルを掛けると、次の式が得られます。



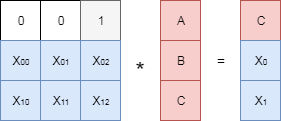
唯一の問題は $$$A$そして $$$B$私たちは失われました、そして、彼らは今私たちに知られていない。 どうやって見つけることができますか？ この問題には非常にエレガントな解決策があります。

生成行列から対応する行を消し、その逆を見つけます。 図では、この逆行列は $$$\ {Y_ {ij} \}$ 。 ここで、元の方程式の左右にこの逆行列を掛けます。



方程式の左側の行列を削減し（逆行列と直接行列の積が単位行列です）、方程式の右側に未知のパラメータがないことを考慮して、目的の式を取得します $$$A$そして $$$B$。



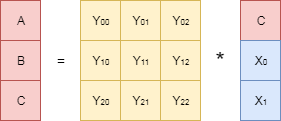
実際、今行ったことは、データストレージシステムで使用されるすべてのタイプのリードソロモンコードの基礎です。 コーディングプロセスが冗長データを検出しています $$$X_0$、 $$$X_1$、デコードプロセスは逆行列を見つけて、「保存された」データのベクトルを掛けます。

考慮されたスキームは、任意の量の「初期」および「冗長」データに一般化できることに気付くのは簡単です。 つまり、元の $$$N$数字を作ることができます $$$K$過剰、および任意の損失を復元することが常に可能です $$$K$から $$$N + K$数字。 この場合、生成行列のサイズは $$$（N + K）×N$、および行列の上部は $$$N×N$シングルになります。

生成行列の構築の問題に戻りましょう。 数字を選べますか $$$X_ {ij}$どうにかして？ 答えはノーです。 それらは、削除する行に関係なく、マトリックスが反転可能なままになるように選択する必要があります。 幸いなことに、私たちが必要とする特性を備えた行列のタイプは、数学で長い間知られていました。 たとえば、 コーシー行列 。 この場合、エンコード方法自体は、しばしばCauchy-Reed-Solomonメソッドと呼ばれます。 同じ目的で、Vandermondeマトリックスが使用されることもあるため、Vandermonde-Reed-Solomonと呼ばれます。

次の問題に移りましょう。 コンピューター内の数値を表すために、固定バイト数が使用されます。 したがって、私たちのアルゴリズムでは、任意の有理数、さらには実数で自由に操作することはできません。 このようなアルゴリズムをコンピューターに実装することはできません。 私たちの場合、生成マトリックスは整数で構成されていますが、このマトリックスを反転すると、有理数が発生する場合があり、コンピューターのメモリで表現するのは困難です。 それで、有名なガロア畑が現場に来たとき、私たちはその場所に着きました。

フィールズガロア

それでは、ガロア体とは何ですか？ 説明用の例からもう一度始めましょう。 私たちは皆、自然数、合理的数、実数などの数を使った操作（加算、減算、乗算、除算など）に慣れています。 ただし、通常の数の代わりに、オブジェクトの任意のセット（有限および/または無限）を検討し、これらのセットに加算、減算などに類似した操作を導入できます。 実際、グループ、リング、フィールドなどの数学的構造は特定の操作が導入されるセットであり、これらの操作の結果は元のセットに属します。 たとえば、自然数のセットでは、加算、減算、乗算の標準操作を導入できます。 結果は再び自然数になります。 しかし、2つの自然数を除算すると、結果は小数になる可能性があります。

フィールドは、加算、減算、乗算、除算の操作が指定されるセットです。 例は、有理数（分数）のフィールドです。 ガロア体-有限体（有限数の要素を含む集合）。 通常、ガロア体は次のように示されます $$$Gf（p）$どこで $$$p$-フィールド内の要素の数。 必要な次元のフィールドを構築するためのメソッドが開発されました（可能な場合）。 このような構成の最終結果は、通常、加算テーブルと乗算テーブルであり、フィールドの3番目の要素をフィールドの2つの要素に関連付けます。

疑問が生じるかもしれません-これをどのように使用するのでしょうか？ コンピューターにアルゴリズムを実装する場合、バイトを使用すると便利です。 アルゴリズムは入力を取ることができます $$$N$ソースデータのバイトとそれらから計算 $$$K$冗長バイト。 1バイトには256の異なる値を含めることができるため、フィールドを作成できます $$$Gf（2 ^ 8）$超過分を計算します $$$K$ガロア体の算術を使用したバイト。 データのエンコード/デコード（生成行列の構築、行列の反転、列による行列の乗算）へのアプローチは以前と同じです。

さて、私たちは基本から学びました $$$N$追加を構成するバイト $$$K$失敗した場合に使用できるバイト。 実際のストレージではどのように機能しますか？ 実際のストレージシステムでは、通常、固定サイズのデータ​​ブロックで動作します（異なるシステムでは、このサイズは数十メガバイトからギガバイトまで変化します）。 この固定ブロックは、 $$$N$フラグメントおよび追加 $$$K$フラグメント。

フラグメントを構築するプロセスは次のとおりです。 それぞれから1バイトを取得します $$$N$オフセット0の初期フラグメント。このデータからK個の追加バイトが生成され、それぞれがオフセット0の対応する追加フ​​ラグメントに移動します。このプロセスは、オフセット-1、2、3、...に対して繰り返されます。異なるドライブ。 これは次のように表すことができます。



1つまたは複数のディスクに障害が発生すると、対応する失われたフラグメントが再構築され、他のディスクに保存されます。

理論的な部分は徐々に終わりに近づいています。リードソロモンコードを使用してデータをエンコードおよびデコードする基本原理が多かれ少なかれ明確になることを期待しましょう。 このトピックに関心がある場合、以下の部分では、ガロア体の計算、特定のハードウェアプラットフォームでのエンコード/デコードアルゴリズムの実装、および最適化手法について詳しく説明することができます。

UPD トピックに関する解説からの参照（ whitedruidに感謝）：
-「コーディングの代数理論」、Berlekamp E.、1971
-「エラー訂正コードの理論」、Mc-Williams F.、Sloan N.J.、1979
-「エラー制御コードの理論と実践」、1986年。
-「ノイズレスコーディングの技術。 メソッド、アルゴリズム、アプリケーション」、Morelos-Zaragoza R.、2005年。
-「デジタル通信システムのエラー訂正を使用したコーディング」、クラークJ.、ケインJ.、1987
-「ボール、グレーティング、グループのパッキング」、Conway J.N.、Sloan N.J.A.、1990
whitedruid ： 比較的最近、「Packing Balls、 Lattices and Groups」 という 本を読みました 。本当に気に入りました。
-「 代数コード入門 」 -MIPTの教師であるYuri Lvovich Sagalovichの講義。本の形でデザインされています。
-「 素人の視点からのリードソロモンコード 」- 簡単な言語で書かれています。
-「 エラーを修正するコード 」- 簡潔に、明確に、写真付きで:)
-「 コーディング理論に関する注意事項 」、A。Romashchenko、A。Rumyantsev、A。Shen、2011年。 -一種の「チートシート」- 簡潔に、容量的に、しかしある程度の準備が必要です。
-また、 「コーディング理論」に関するセミナーを無視することはできません。これは、情報伝送問題研究所のスタッフによって定期的に開催されています。 A.A. ロシア科学アカデミーのハルケビッチ」、モスクワ。 さらに-リンクを介して-コーディングの数学的理論に関連するトピックに関する多くの興味深いトピックを見つけることができます;トピックの問題はこの分野で提起されます。 たとえば、極および拡張リードソロモンコードの順次デコードについて 。 検索エンジンでは、著者による記事をすでに見つけることができます。