
重量スペクトルを計算するプロセス
根本原因
この記事は、ロシア語を話すサポートのWolfram Mathematicaグループで尋ねられたかなり古い質問の 1つに由来しています。 しかし、それに対する答えは大きく成長し、最終的には自立した生活を送り始め、独自の問題さえも抱え始めました。 記事のタイトルから明らかなように、タスクは重みスペクトルの計算に専念しました。つまり、離散数学と線形代数に直接関連しています。 また、Wolfram言語ソリューションのデモも行います。 問題の本質は非常に単純であるという事実にもかかわらず(単純な基本ベクトルの場合は完全に頭の中で解決されます)、重みスペクトルを見つけるためのアルゴリズムを最適化するプロセスは非常に重要です。 著者は、この記事で検討した問題とその解決方法が、Wolframでコンパイルや並列化などの手法を使用する方法を非常によく示していると考えています。 したがって、主な目標は、Mathematicaでコードを高速化する効果的な方法の1つを示すことです。
問題の最初の声明を引用します。
a)ベクトルは、固定長Nのビット列(値0または1)です。つまり、合計2 N個の異なるベクトルが可能です。
b)2つのベクトルを法とする加算演算(演算xor)を導入します。2つのベクトルaとbで、同じ長さNのベクトルa + bを受け取ります。
c)集合A = {a i | 0≤K≤2 N個のベクトルからi∈1..K}。 生成と呼びます:セットAのa iを追加することにより、form i = 1..K b i a iの形式の2 Kベクトルを取得できます。ここで、b iは0または1です。
d)ベクトルの重みは、ベクトルの単位(ゼロ以外)ビットの数です。つまり、重みは0からNまでの自然数です。
ベクトルのセットと数Nの指定されたジェネレーターは、重みによって異なるベクトルの数のヒストグラム(スペクトル)を作成する必要があります。
入力フォーマット:
同じ長さの行のセットからのテキストファイル、行ごとに1つのベクトル(区切り文字なしの文字0および1)。
出力形式:
タブ文字で区切られた重量/数値のペアを含むテキストファイル。1行に1つのペアがあり、数値の重量値でソートされています。
手動ソリューション
最初に、重量スペクトルを計算する原理を理解するために、心の問題を解決してみましょう。 このために、最小長のベクトルを使用します。 次に、任意の数のベクトルと任意の次元のアルゴリズムを拡張する必要があります。 それぞれに2つの要素を持つ2つのベクトルの基底を与えます:
basis = {{0, 1}, {1, 1}}
ベクトルは2つしかないため、可能なすべての線形結合、およびそれに応じて、b iの値の組み合わせは2 Kになります(Kは基底ベクトルの数)。 次の線形結合のうち4つを取得します。
mod2(0 * {0, 1}, 0 * {1, 1}) = {0, 0} mod2(0 * {0, 1}, 1 * {1, 1}) = {1, 1} mod2(1 * {0, 1}, 0 * {1, 1}) = {0, 1} mod2(1 * {0, 1}, 1 * {1, 1}) = {1, 0}
ここでは、モジュロ2加算関数がすでに適切に定義されていると仮定しています。 4つのベクトルが判明し、それぞれの次元は2に等しくなります。 最終的にスペクトルを計算するには、結果の各ベクトルのユニット数を計算するだけです。
sum({0, 0}) = 0 sum({1, 1}) = 2 sum({0, 1}) = 1 sum({1, 0}) = 1
結果の各重みのリストのエントリ数を計算します。 そして、タスクの要件に応じて、結果は次のようになります。
{{0, 1}, {1, 2}, {2, 1}}
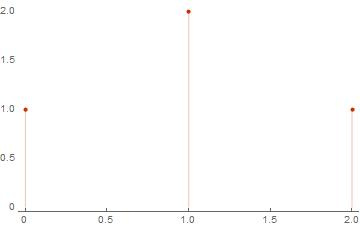
Wolfram Mathematicaでの単純なアルゴリズムの実装
それで、今や心の中で行われていることはすべて、Wolfram言語を使用して記録と自動化を試みます。 最初に、2を法とする加算を実行する関数を作成します(問題ステートメントで述べたように)。
(* *) mod2[b1_Integer, b2_Integer] := Mod[b1 + b2, 2] (* *) mod2[b1_Integer, b2__Integer] := mod2[b1, mod2[b2]] (* - *) Attributes[mod2] := {Listable}
次の関数は、入力としてベクトルのリストと係数b iのリスト(長さが基底内のベクトルの数に等しいベクトル)を取る必要があります。 基底の要素と同じ次元のベクトルを返すことは線形結合です。
(* *) combination[basis: {{__Integer}..}, b: {__Integer}] /; Length[basis] == Length[b] := Apply[mod2, Table[basis[[i]] * b[[i]], {i, 1, Length[b]}]]
次に、係数b iのすべての可能なセットのリストを取得する必要があります。 明らかに、それらの数は2 Kであり、可能なすべてのセットは、バイナリ表現で0から2 K -1までのすべての数の単なる記録です。 次に、すべての可能な線形結合のリストを次のように取得できます。
linearCombinations[basis: {{__Integer}..}] := With[{len = Length[basis]}, Table[combination[basis, IntegerDigits[i, 2, len]], {i, 0, 2^len - 1}] ]
上記の関数の結果は、2 Kベクトルのリストです。 あとは、このリストの各ベクトルの重みを計算し、各重みの会議の数を計算するだけです。
weightSpectrum[basis: {{__Integer}..}] := Tally[Map[Total, lenearCombination[basis]]];
それがどのように機能するかを確認しましょう。 ランダムベクトルのリストから基底を作成し、重みスペクトルを計算します。
(* *) basis = RandomInteger[{0, 1}, {6, 6}] ws = weightSpectrum[basis] ListPlot[ws, PlotTheme -> "Web"] (* Out[..] := {{0, 0, 1, 1, 1, 0}, {1, 0, 0, 0, 0, 1}, {1, 1, 0, 1, 0, 1}, {1, 0, 0, 1, 1, 0}, {1, 0, 0, 0, 1, 1}, {0, 1, 0, 1, 1, 1}} Out[..]:= {{0, 1}, {4, 15}, {3, 20}, {2, 15}, {1, 6}, {5, 6}, {6, 1}} *)
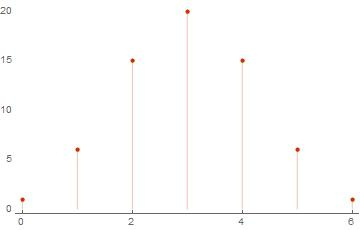
しかし、同じことを計算しようとすると、より多くのベクトルについてはどうなりますか? AbsoluteTiming []関数を使用して、計算時間が基底のサイズにどのように依存するかを確認します。
basisList = Table[RandomInteger[{0, 1}, {i, 10}], {i, 1, 15}]; timeList = Table[ {Length[basis], First[AbsoluteTiming[weightSpectrum[basis]]]}, {basis, basisList} ]; ListPlot[timeList, PlotTheme -> "Web", Joined -> True]
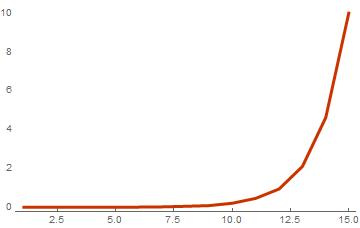
同じ長さのベクトルに対する計算時間の基底のサイズへの依存
結果のグラフでわかるように、計算時間は、基底のベクトルの数を追加すると指数関数的に増加します。 各ベクトルに10個の要素がある15個のベクトルに基づいて、スペクトルの計算は約10秒間続きます。 このような計算時間は非常に長くなりますが、線形結合の数は基底のサイズとともに指数関数的に増加し、したがって同じ数の操作の数が増加すると既に言われているため、これには驚くべきことはありません。 計算速度を低下させるもう1つの要因は、コードが最適ではないことです。 Wolfram言語はインタプリタ型プログラミング言語であるため、最初は十分に高速とは見なされていません。つまり、標準関数では最大のパフォーマンスが得られません。 この問題を解決するために、コンパイルを使用します。
コンパイルされた関数を使用する
この関数の構文は非常に単純で、 Functionに非常に似ています。 その結果、 Compileは常に「オブジェクト」、つまり数値または数値のリストに適用できるコンパイル済み関数を返します。 コンパイルは、文字列、文字、または複合Wolfram言語式( Listで構成される式を除く)の操作をサポートしません。 以下は、コンパイル済み関数の作成例です。
cSqr = Compile[{x}, x^2]; cSqr[2.0] (* Out[..] := 4.0 *) cNorm = Compile[{x, y}, Sqrt[x^2 + y^2]]; cNorm[3.0, 4.0] (* Out[..] := 5.0 *) cReIm = Compile[{{z, _Complex}}, {Re[z], Im[z]}]; cReIm[1 + I] (* Out[..] := {1.0, 1.0} *) cSum = Compile[{{list, _Real, 1}}, Module[{s = 0.0}, Do[s += el, {el, list}]; s]]; cSum[{1, 2, 3.0, 4.}] (* Out[..] := 10.0 *)
使用可能なすべてのオプションと詳細な例は、上記のリンクの公式ドキュメントに記載されています。 次に、重みスペクトルを計算するための関数に直接渡します。
重量スペクトルの計算の編集
単純な場合と同様に、いくつかの単純な関数を作成し、それらを順番に適用して結果を取得できます。 また、1つの関数の本体ですべての操作を実行できます。 それと別の方法の両方を実現できます。 多様性のために、2番目の方法に進みます。
cWeightSpectrumSimple = Compile[ {{basis, _Integer, 2}}, Module[ { k = Length[basis], spectrum = Table[0, {i, 0, Last[Dimensions[basis]]}] }, Do[ With[ { (* 2^k - 1 *) weight = Total[Mod[Total[IntegerDigits[b, 2, k] * basis], 2]] + 1 }, (* spectrum . weight - 1 , . spectrum . , . *) spectrum[[weight]] = spectrum[[weight]] + 1 ], {b, 0, 2^k - 1} ]; Return[Transpose[{Range[0, Last[Dimensions[basis]]], spectrum}]] ] ]
いつものように、この関数の正しい動作の小さなテストを実施します。 同様に、2〜15個のベクトルのサイズを持つランダムなベースのリストを取得します。各ベクトルは10個の要素で構成され、重みスペクトルが計算される時間を計算します。
basisList = Table[RandomInteger[{0, 1}, {i, 10}], {i, 2, 15}]; timeList=Table[{Length[basis],First[AbsoluteTiming[cWeightSpectrumSimple[basis]]]},{basis,basisList}]; ListLinePlot[timeList, PlotTheme -> "Web"]
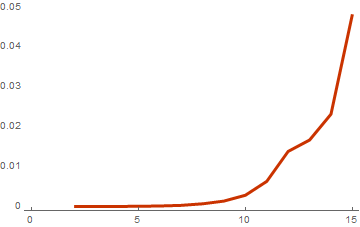
最後のグラフからわかるように、前の部分の結果との違いは非常に大きいです。 最終段階での最適な重量計算とコンパイルの使用という形でアルゴリズムを少し最適化すると、200倍の加速が得られます。 この結果は、一方で、Mathematicaが正しく使用されている場合、かなり高速な言語として表示され、もう一方では、関数の内部動作の複雑さを知らない場合、その解釈可能性のためにMathematicaが低速言語であることをもう一度証明するという点で興味深いです
グレーコード
グレイコードについて
問題を解決する方法を考えながら、簡単な考えが生まれました。 b iの次の値が突然ゼロになった場合、基底ベクトルにこの数値を掛けて加算する必要はありません。 ゼロ値で乗算されたこれらのベクトルは、結果を変更しません。 最初はすばらしい考えのように思えたが、うまくいった。 確かに、リストb iの要素の列挙中に、ベクターの追加操作は単純に出てきました。 その後、次のアイデアが生まれました。 線形結合を計算するときにベクトルを減算および追加することも同じです。 これは、以下が実行可能であることを意味します。
1 * {0, 1} + 0 * {1, 0} + 1 * {1, 1} == {0, 1} + {1, 1} {0, 1} + {1, 1} == {1, 0} -> {1, 0} + {1, 1} == {0, 1}
つまり、小計にベクトルを追加しても、減算と同じです。 そして、すべてが素晴らしいアイデアになりました! リストb iのサイクルで、 b kとb k + 1の表現の違いがほんの数ビットであることが突然判明した場合はどうでしょうか。 次に、番号kの線形結合を取得し、インデックスがkとk + 1の間の異なるビットの番号と一致する基底ベクトルのみに追加します。 結果はk + 1の線形結合です。 しかし、さらに先に進むとどうなりますか? 突然、隣接する線形結合の違いがたった1つのベクトルであることがわかりました。 0から2 N -1の直接シーケンスを作成する場合、これは不可能です。 しかし、これらの数値を他の順序で組み合わせて配置できるとしたらどうでしょうか? これが判明したように、これはグレイコードと呼ばれます-隣人の間の差が1つのカテゴリーにすぎない数字のシーケンス。 ウィキペディアには、無数のコードの1つであるグレーミラーコードとその取得方法が記載されています。 以下は、そのようなシーケンスの例です。
| 小数 | バイナリ | 灰色 | 10進数としての灰色 |
|---|
| 0 | 000 | 000 | 0 |
| 1 | 001 | 001 | 1 |
| 2 | 010 | 011 | 3 |
| 3 | 011 | 010 | 2 |
| 4 | 100 | 110 | 6 |
| 5 | 101 | 111 | 7 |
| 6 | 110 | 101 | 5 |
| 7 | 111 | 100 | 4 |
コンパイル済み関数で使用
コンパイルを使用すると、すでに重みスペクトルの計算が大幅に高速化されています。次に、グレーコードを使用して線形結合ベクトルの追加を最適化してみましょう。 各ステップで変更されたビットの位置を計算する方法を理解する必要があります。 幸いなことに、この本の第13章が助けになりました。 線形結合全体は、最初に1回だけカウントする必要があります。 ただし、最初の線形結合がゼロのセットであることは確かにわかっているため、これは必要ありません。 上記に基づいて、重量スペクトルを計算するためのさらに最適化された関数を作成できます。
WeightSpectrumLinearSubspaceGrayCodeEasy = Compile[{{basevectors, _Integer, 2}}, Module[{ n = Dimensions[basevectors][[-1]], k = Length[basevectors], s = Table[0, {n + 1}], currentVector = Table[0, {n}], (* {0, 0, ..}*) m = 0, l = 0 }, (* , 0 1 *) s[[1]] = 1; Do[ (* *) m = Log2[BitAnd[-1 - b, b + 1]] + 1; (* , *) currentVector = BitXor[currentVector, basevectors[[m]]]; (* *) l = Total[currentVector] + 1; s[[l]] = s[[l]] + 1, {b, 0, 2^k - 2} ]; (* Return *) s ], (* , *) RuntimeOptions -> "Speed", (*CompilationTarget -> "C",*) CompilationOptions -> {"ExpressionOptimization" -> True} ];
次元512の16個のベクトルの基底の結果の例を次に示します。
basis = RandomInteger[{0, 1}, {16, 512}]; ListPlot[WeightSpectrumLinearSubspaceGrayCodeEasy[basis], PlotTheme -> "Web", PlotRange -> All, Filling -> Bottom]
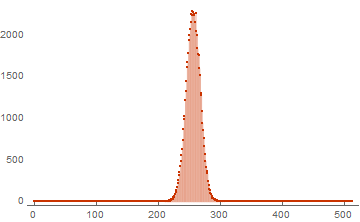
その結果、重みの1次元リストが返されます。 この種のリストは、前の部分から簡単に表示できるため、非常に正確です。 最初の要素は、ゼロの重みベクトルの出現頻度に対応します。 後者は、ユニットのベクトルの発生頻度です。 同じコードを使用してパフォーマンスをテストします。
basisList = Table[RandomInteger[{0, 1}, {i, 10}], {i, 2, 15}]; timeList=Table[{Length[basis],First[AbsoluteTiming[WeightSpectrumLinearSubspaceGrayCodeEasy[basis]]]},{basis,basisList}]; ListLinePlot[timeList, PlotTheme -> "Web"]
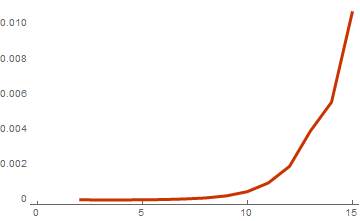
基底のサイズからの計算時間
その結果、15個のベクトルのリストの最後のベースでは、計算速度がさらに5倍に増加しました。 しかし、これは少し誤解を招く結果です。 効率がどれだけ改善されたかを理解するには、最後の2つの関数の計算時間の比率を計算する必要があります。
basisList = Table[RandomInteger[{0, 1}, {i, 10}], {i, 2, 20}]; timeList=Table[{ Length[basis], First[RepeatedTiming[cWeightSpectrumSimple[basis]]] / First[RepeatedTiming[WeightSpectrumLinearSubspaceGrayCodeEasy[basis]]] }, {basis,basisList} ]; ListLinePlot[timeList, PlotTheme -> "Web"]
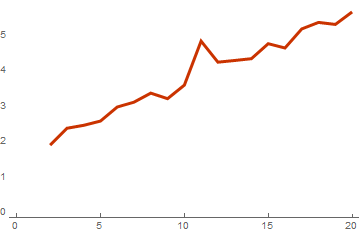
グレイコードを使用した場合と使用しない場合のスペクトル計算の時間の比率
このグラフから、実際にこのアルゴリズムが計算の複雑さを1度削減したことが明らかになります。 そして、これは基底のベクトルの次元が大きいほど顕著で効果的です。 基底が128次元のベクトルで構成される場合の結果は次のとおりです。
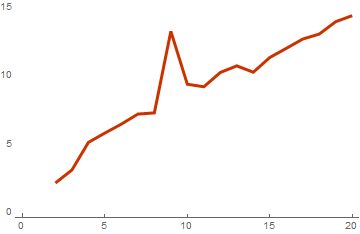
並列化
Mathematicaで何かを並行して計算する方法
Mathematicaには、異なるコアで非同期計算を実行できる小さな関数セットがあります。 今だけ用語で定義する必要があります。 結局、実行中のプロセスは、Mathematicaの仮想マシンに似たものであり、カーネルとも呼ばれます。 カーネル。 数学の中核は、インタプリタモードで動作するインタラクティブランタイムです。 各コアは、システム内の1つのプロセスである必要があります。 通常の意味での言語はフローを実現しません。 したがって、標準使用のコアには共有メモリがないことを理解する必要があります。 基本的に、このタイプのすべての関数はParallelで始まります。 非同期的に何かをカウントする最も簡単な方法:
ParallelTable[i^2,{i, 1, 10}] (*Out[..] := {1, 4, 9, 16, 25, 36, 49, 64, 81, 100}*)
多くの機能が同様に機能します。
ParallelMap 、 ParallelDo 、 ParallelProduct 、 ParallelSum 、...
これが実際に複数のコアで実行されたことを確認するには、いくつかの方法があります。 これは、実行中のすべてのカーネルを取得する方法です。
Kernels[] (* Out[..] := {"KernelObject"[1, "local"], ... , "KernelObject"[N, "local"]} *)
リストには、現在実行中のすべてのプロセスが含まれます。 同時に、タスクマネージャーにも表示される必要があります。

6つのプロセスのうち2つが実行中のセッションを担当し、残りは並列コンピューティングに使用されるローカルカーネルです。 この場合、デフォルトでは、ローカルMathematicaコアの数は物理プロセッサコアの数と一致します。 しかし、だれも大きな数を作成することを気にしません。 これはLaunchKernels [n]を使用して行われます。 その結果、 追加の n個のコアが起動されます。 また、利用可能なプロセッサコアの数は、 $ KernelCount変数で確認できます。
最初にリストされた関数は、プロセス間でタスクを自動的に分散します。 ただし、特定のカーネルで実行するコードを個別に送信する方法があります。 これはParallelEvaluate + ParallelSubmitを使用して行われます。
ParallelEvaluate[$KernelID, Kernels[][[1 ;; 4 ;; 2]]] (* Out[..] := {1, 3}*)
この一連の関数は、重みスペクトルの計算タスクを並列化するのに十分です。
メインサイクルのパーツへの分離
計算が実際に並行して行われるかどうかを確認します。 4つの物理コアの場合、これは4つのコアすべての計算に1つのコアと同じ時間がかかることを意味します。
basis = RandomInteger[{0, 1}, {24, 24}]; AbsoluteTiming[WeightSpectrumLinearSubspaceGrayCodeEasy[basis];][[1]] AbsoluteTiming[ParallelEvaluate[WeightSpectrumLinearSubspaceGrayCodeEasy[basis]];][[1]] (* Out[..] := 6.518... Out[..] := 8.790...*)
時間差はありますが、4倍ではありません。 これで、すべてがうまくいきました。 次のステップは、タスクをいくつかの部分に分割する方法を理解することです。 最も論理的で効果的なのは、各コアで線形結合の一部のみを計算することです。 つまり、結果として、各コアは部分的なスペクトルを返します。 しかし、リストb iを分割する方法。 結局のところ、それは直接的なシーケンスではありません! この場合、インデックスごとにグレイコードシーケンスから値を計算する関数が必要です。 これは次のように行われます。
grayNum[basis_List, index_Integer] := IntegerDigits[BitXor[index, Quotient[index, 2]], 2, Length[basis]] Grid[Table[{i, Row[grayNum[{{0, 0}, {0, 1}, {1, 1}}, i]]}, {i, 0, 7}]]
| インデックス | コード |
|---|
| 0 | 000 |
| 1 | 001 |
| 2 | 011 |
| 3 | 010 |
| 4 | 110 |
| 5 | 111 |
| 6 | 101 |
| 7 | 100 |
次に、線形結合の特定の範囲のインデックス内の部分スペクトルのみを考慮するように、コンパイルされた関数を変更します。
WeightSpectrumLinearSubspaceGrayCodeRange = Compile[{{basis, _Integer, 2}, {range, _Integer, 1}}, Module[{ n = Dimensions[basis][[-1]], k = Length[basis], s = Table[0, {n + 1}], currentVector = Table[0, {i, 1, Length[basis[[1]]]}], m = 0, l = 0 }, (* *) If[range[[1]] =!= 0, currentVector = Mod[Total[basis Reverse[IntegerDigits[BitXor[range[[1]], Quotient[range[[1]] + 1, 2]], 2, k]]], 2]; ]; Mod[Total[basis IntegerDigits[BitXor[range[[1]] - 1, Quotient[range[[1]] - 1, 2]], 2, k]], 2]; s[[Total[currentVector] + 1]] = 1; Do[ m = Log2[BitAnd[-1 - b, b + 1]] + 1; currentVector = BitXor[currentVector, basis[[m]]]; l = Total[currentVector] + 1; s[[l]] = s[[l]] + 1, {b, First[range], Last[range] - 1, 1} ]; (* Return *) s ], (* , *) RuntimeOptions -> "Speed", (*CompilationTarget -> "C",*) CompilationOptions -> {"ExpressionOptimization" -> True} ];
つまり、以前に関数が0〜2 N -1の番号を持つすべての組み合わせをカウントした場合、この範囲は手動で設定できます。 次に、使用可能なコアの数に応じて、この同じ範囲を等しい部分に分割する方法を考えてみましょう。
partition[{i1_Integer, iN_Integer}, n_Integer] := With[{dn = Round[(iN - i1 + 1)/n]}, Join[ {{i1, i1 + dn - 1}}, Table[{dn * (i - 1), i * dn - 1}, {i, 2, n - 1}], {{(n - 1) * dn, iN}} ] ]
ここで、そのような画像の完全なスペクトルを計算するには、各セグメントでそれを計算し、すべての結果を追加する必要があります。 例:
WeightSpectrumLinearSubspaceGrayCodeEasy[{{1, 1}, {1, 1}, {1, 1}}] WeightSpectrumLinearSubspaceGrayCodeRange[{{1, 1}, {1, 1}, {1, 1}}, {0, 3}] WeightSpectrumLinearSubspaceGrayCodeRange[{{1, 1}, {1, 1}, {1, 1}}, {4, 7}] (* Out[..] := {4, 0, 4} = Out[..] := {2, 0, 2} + Out[..] := {2, 0, 2} *)
最後のステップは、これらの計算を異なるカーネルに送信することです。
WeightSpectrumLinearSubspaceGrayCodeParallel[basis: {{__Integer}..}] := With[{ kernels = (If[Kernels[] === {}, LaunchKernels[]]; Kernels[]), parts = partition[{0, 2^Length[basis] - 1}, Length[Kernels[]]] }, Total[WaitAll[Table[ ParallelEvaluate[ParallelSubmit[WeightSpectrumLinearSubspaceGrayCodeRange[basis, parts[[$KernelID]]]], kernel], {kernel, kernels} ]]] ]
ここで明確にする必要があります。 このようなバンドルは、どのカーネルがコードのどの部分で実行されるかを手動で制御するためのParallelEvaluate + ParallelSubmitです。 一般的な場合のParallelEvaluateは、非同期コードを正しく実行する方法を理解できず、結果として1つのスレッドで実行します。 また、一般的なケースのParallelSubmitでは、正確なカーネルを指定することはできませんが、自動的に選択します。
この機能が機能するかどうかを確認します。
ListPlot[WeightSpectrumLinearSubspaceGrayCodeParallel[RandomInteger[{0, 1}, {16, 128}]], PlotRange -> All, PlotTheme -> "Web", Filling -> Bottom]
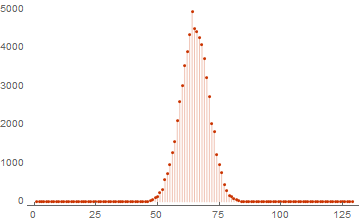
そしていつものように、計算速度の違いを見てみましょう。 4コアプロセッサを搭載したラップトップが使用されるため、加速は約4倍になると予想されます。 さらに、タスクを分割して最終結果を合計する時間を考慮する必要があります。
basis = RandomInteger[{0, 1}, {20, 1024}]; AbsoluteTiming[WeightSpectrumLinearSubspaceGrayCodeEasy[basis];] AbsoluteTiming[WeightSpectrumLinearSubspaceGrayCodeParallel[basis];] (* Out[..] := {5.02..., Null} Out[..] := {1.5....., Null} *)
当然、プロセッサコアの数が多くなると、違いはより顕著になります。 それでは、基底のスペクトルをさらに計算してみましょう。 どのくらい時間がかかるのだろうか? 1つの計算を完了するのに1分以上かかるまで、基底のサイズを大きくすると仮定します。
spectrums = Block[{i = 1, basis, res}, Reap[ While[True, i++; basis = RandomInteger[{0, 1}, {i, i}]; Sow[res = AbsoluteTiming[WeightSpectrumLinearSubspaceGrayCodeParallel[basis]]]; If[res[[1]] > 60, Break[]] ] ][[-1, -1]]] ListPlot[spectrums[[-1, -1]], PlotLabel->Row[{"basis len: ", Length[spectrums] + 1, "; time: ", Round[spectrums[[-1, 1]], 0.01], " sec"}], Filling->Bottom,PlotTheme->"Web",PlotRange->All]
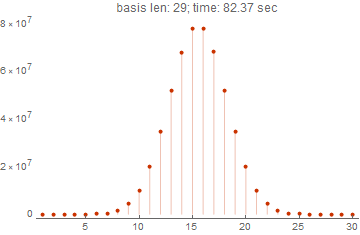
この図は、関数が29のベクトルに基づいてスペクトルを1分半で計算できることを明確に示しています。 これは、コンパイルを使用しない最初のオプションであるグレイコード(並列化)が妥当な時間内に同じことを完了することができないため、非常に良い結果です。 10次元の15個のベクトルでさえ計算に10秒以上かかった場合、計算時間は数千倍になります。
おわりに
誰が、どこで記事に記載されているすべてのものを適用するのかわかりません。 ウィキペディアによると、グレイコードには実用的な目的があるとのことです。 また、スペクトルの計算は、暗号化や線形代数の他の問題に関連していることが多いことも知っています。 , , : , . , .
PS , .