独自の物理2Dエンジンを作成します。 パート1：力パルスの基礎と分解能

さまざまな理由で、独自の物理エンジンの作成を開始できます。まず、数学、物理学、プログラミングの新しい知識の開発と同化。 次に、独自の物理エンジンが、作成者が作成できる技術的効果を処理できます。 この入門記事では、独自の物理エンジンをゼロから作成する方法を紹介します。

物理学はプレイヤーにゲームに没頭するための途方もない機会を与えます。 物理エンジンをマスターすることは、プログラマーにとって非常に役立つスキルになると思います。 エンジンの内部操作をより深く理解するために、いつでも最適化や特殊な機能を作成できます。

チュートリアルのこのパートでは、次のトピックについて説明します。

• 簡単な衝突検出
• 単純な品種の生成
• インパルス分解能を強制する

ここに小さなデモがあります：


注：このチュートリアルはC ++で書かれていますが、ほぼすべてのゲーム開発環境で同じ手法と概念を使用できます。

---

必要な知識

この記事を理解するには、数学と幾何学に関する十分な知識が必要であり、プログラミング自体はそれほど重要ではありません。 特に、次のものが必要です。

• ベクトル数学の基本の基本的な理解
• 代数計算を実行する機能

---

衝突認識

インターネットには衝突認識に関する十分な記事とチュートリアルがありますので、このトピックを詳細に検討することはしません。

座標軸に合わせた境界矩形

座標軸に揃えられた境界ボックス（Axis Aligned Bounding Box、AABB）は、4つの軸が配置されている座標系に揃えられた長方形です。 これは、長方形が回転できず、常に90度の角度にあることを意味します（通常は画面に合わせて配置されます）。 AABBは他のより複雑な形状を制限するために使用されるため、通常は「境界ボックス」と呼ばれます。


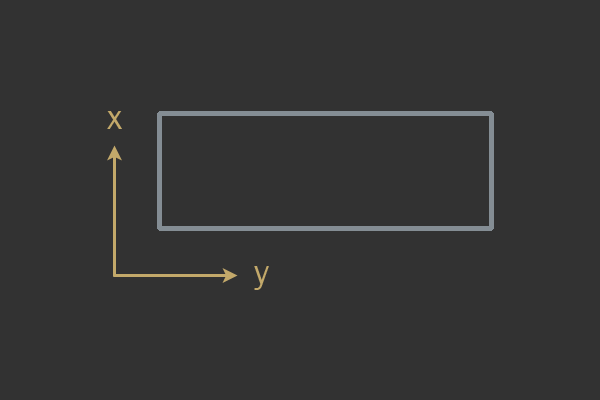AABBの例。

複雑なAABBは、より複雑なフォームがAABB内で交差できるかどうかを確認するための簡単なチェックとして使用できます。 ただし、ほとんどのゲームの場合、AABBは基本的な形式として使用され、実際には何も制限しません。 AABBの構造は非常に重要です。 AABBを指定する方法はいくつかありますが、ここに私のお気に入りを示します。

struct AABB { Vec2 min; Vec2 max; }; 

この形式では、2つのポイントでAABBを指定できます。 ポイントminはx軸とy軸に沿った下限を示し、maxは上限を示します。つまり、左上隅と右下隅を示します。 2つのAABBが交差するかどうかを判断するには、分離軸定理（SAT）の基本的な理解が必要です。

以下は、SATを使用するChristopher Erickson リアルタイム衝突検出サイトからの簡単なチェックです。

 bool AABBvsAABB( AABB a, AABB b ) { //   ,      if(a.max.x < b.min.x or a.min.x > b.max.x) return false if(a.max.y < b.min.y or a.min.y > b.max.y) return false //    ,         return true } 

サークル

円は、半径と点によって定義されます。 円構造は次のようになります。

 struct Circle { float radius Vec position }; 

2つの円の交差を確認するのは非常に簡単です。2つの円の半径を取得して追加し、円の2つの中心間の距離の合計が大きいかどうかを確認します。

平方根演算子を取り除くための重要な最適化：

 float Distance( Vec2 a, Vec2 b ) { return sqrt( (ax - bx)^2 + (ay - by)^2 ) } bool CirclevsCircleUnoptimized( Circle a, Circle b ) { float r = a.radius + b.radius return r < Distance( a.position, b.position ) } bool CirclevsCircleOptimized( Circle a, Circle b ) { float r = a.radius + b.radius r *= r return r < (ax + bx)^2 + (ay + by)^2 } 

一般に、乗算は値の平方根を取得するよりもはるかに安価な演算です。

---

インパルス解像度を強制する

インパルス解決は、特定のタイプの衝突解決戦略です。 衝突解決は、交差する2つのオブジェクトを取得して変更し、交差しないようにするアクションです。

一般的な場合、物理エンジン内のオブジェクトには、3つの基本的な自由度 （2次元）があります。xy平面内の動きと回転です。 この記事では、意図的に回転を制限し、円のあるAABBのみを使用するため、考慮する必要がある唯一の自由度はxy平面内の動きです。

検出された衝突を解決するプロセスでは、オブジェクトが互いに交差できないように、移動にこのような制限を課します。 力の衝動を解決する基本的な考え方は、力の衝動（速度の瞬間的な変化）を使用して、衝突が認識されるオブジェクトを分離することです。 これを行うには、何らかの方法で各オブジェクトの位置と速度を考慮する必要があります。衝突時に小さなオブジェクトと交差する大きなオブジェクトが少し移動し、小さなオブジェクトがそれらから飛び出すようにします。 また、無限の質量を持つオブジェクトがまったく動かないようにしたいと考えています。


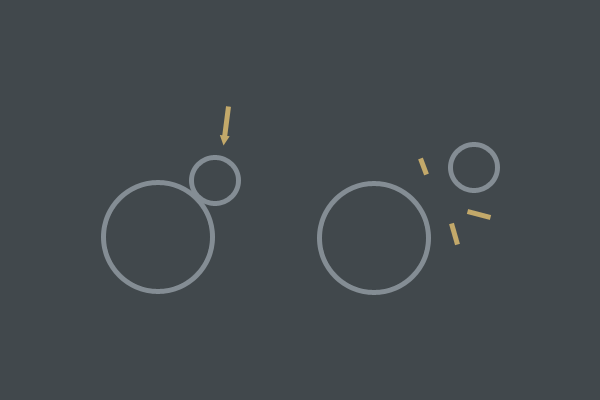力の衝動を解決することで達成できることの簡単な例。

この効果を達成すると同時に、オブジェクトの振る舞いの直感的な理解に従うために、ソリッドと少しの数学を使用します。 ソリッドは、ユーザー（つまり、開発者）によって定義された単純なフォームであり、変形不能として明確に定義されています。 この記事のAABBと円の両方は変形不能であり、常にAABBまたは円のいずれかになります。 すべての圧縮とストレッチは禁止されています。

ソリッドを使用すると、一連の計算を大幅に簡素化できます。 それがゲームでソリッドがよく使用される理由です。したがって、この記事ではソリッドを使用します。

オブジェクトが衝突しました-次は何ですか？

2つの物体の衝突が見つかったとします。 それらを分離する方法は？ 衝突認識は、2つの重要な特性を提供すると想定しています。

• 衝突法線
• 浸透深さ

力の勢いを両方のオブジェクトに適用し、それらを互いに押し離すには、どの方向にどれだけ反発されるかを知る必要があります。 衝突法線とは、力のインパルスが適用される方向です。 浸透の深さは（他のいくつかのパラメーターと一緒に）使用される力の衝撃の大きさを決定します。 つまり、計算する必要があるのは、力の運動量の大きさだけです。

次に、力の運動量の大きさを計算する方法を詳しく見てみましょう。 交差点が検出された2つのオブジェクトから始めましょう。

式1

$$

$$V ^ {AB} = V ^ B-V ^ A$$

位置Aから位置Bへのベクトルを作成するには、 endpoint - startpoint実行する必要があることに注意してください。 $$$V ^ {AB}$ AからBへの相対速度です。この方程式は、衝突の法線を基準にして表現できます。 $$$n$ 、つまり、衝突の法線の方向に沿ったAからBまでの相対速度を知りたい：

式2

$$

$$V ^ {AB} \ cdot n =（V ^ B-V ^ A）\ cdot n$$

ここで、 スカラー積を使用します 。 スカラー積は、コンポーネントごとの積の単純な合計です。

式3

$$

$$V_1 = \ begin {bmatrix} x_1 \\ y_1 \ end {bmatrix}、V_2 = \ begin {bmatrix} x_2 \\ y_2 \ end {bmatrix} \\ V_1 \ cdot V_2 = x_1 * x_2 + y_2 * y_2$$

次のステップは、弾性係数の概念を導入することです。 弾性は、弾性を意味する概念です。 物理エンジンの各オブジェクトには弾力性があり、10進数値で表されます。 ただし、力の運動量の計算には1つの小数値のみが使用されます。

目的の弾力性を選択するには $$$e$ 、「イプシロン」）、直感的に予想される結果を満たしているため、関連する最小の弾性を使用する必要があります。

 //    A  B e = min( A.restitution, B.restitution ) 

受け取ったこと $$$e$ 、力の運動量の大きさを計算するための式に代入することができます。

ニュートンの復元の法則は次のように読みます。

式4

$$

$$V '= e * V$$

衝突後の速度は、衝突前の速度に一定の定数を掛けたものに等しいというだけです。 この定数は「反発係数」を表します。 これを知っていれば、現在の方程式で弾性を簡単に置き換えることができます。

式5

$$

$$V ^ {AB} \ cdot n = -e *（V ^ B-V ^ A）\ cdot n$$

ここに負の値が表示されていることに注意してください。 ここでマイナス記号を導入したことに注目してください。 ニュートンの回復の法則による $$$V '$ 、反発後の結果のベクトルは、実際にはVとは反対の方向に進みます。では、方程式で反対の方向をどのように表現するのでしょうか。 マイナス記号を入力します。

次に、力のインパルスの影響下でこれらの速度を表現する必要があります。 ベクトルをスカラーの運動量力に変更するための簡単な方程式を次に示します $$$j$ 特定の方向に $$$n$ ：

式6

$$

$$V '= V + j * n$$

この方程式は非常に重要なので理解してください。 単位ベクトルがあります $$$n$ 方向を示します。 スカラーもあります $$$j$ ベクトルの長さを示す $$$n$ 。 スケーリングされたベクトルを合計する場合 $$$n$ と $$$V$ 私たちは得る $$$V '$ 。 これは単純に2つのベクトルを加算したものです。この小さな方程式を使用して、1つのベクトルの力の運動量を別のベクトルに適用できます。

ここで、やるべきことが少しあります。 正式には、勢いの勢いは勢いの変化として定義されます。 運動量は * です。 これを知って、次のように正式な定義に従って衝動を表現できます。

式7

$$

$$インパルス=質量*速度\\速度= \ frac {Impulse} {mass} \したがってV '= V + \ frac {j * n} {mass}$$

三角形の形状の3つの点（ $$$\したがって$ ）「したがって」と読むことができます。 この指定は、前のものから次のものの真理を推測するために使用されます。

順調です！ ただし、力の勢いを次のように表現する必要があります。 $$$j$ 2つの異なるオブジェクトに関連します。 オブジェクトAとオブジェクトBの衝突中、オブジェクトAはBとは反対方向に反発されます。

式8

$$

$$V '^ A = V ^ A + \ frac {j * n} {mass ^ A} \\ V' ^ B = V ^ B-\ frac {j * n} {mass ^ B}$$

これらの2つの方程式は、単位方向ベクトルに沿ってBからAをはじきます $$$n$ 力の運動量のスカラーごと（量 $$$n$ ） $$$j$ 。

これはすべて、式8と5を組み合わせるために必要です。最終的な式は次のようになります。

式9

$$

$$（V ^ A-V ^ V + \ frac {j * n} {mass ^ A} + \ frac {j * n} {mass ^ B}）* n = -e *（V ^ B-V ^ A ）\ cdot n \\ \したがって\\（V ^ A-V ^ V + \ frac {j * n} {mass ^ A} + \ frac {j * n} {mass ^ B}）* n + e * （V ^ B-V ^ A）\ cdot n = 0$$

覚えている場合、元の目標は値を分離することでした。なぜなら、衝突を解決する必要がある方向がわかっているためです（衝突の認識によって決定されます）。この方向の値を決定するだけです。 私たちの場合、未知の値 $$$j$ ; 強調する必要があります $$$j$ 彼女の方程式を解きます。

式10

$$

$$（V ^ B-V ^ A）\ cdot n + j *（\ frac {j * n} {mass ^ A} + \ frac {j * n} {mass ^ B}）* n + e *（V ^ B-V ^ A）\ cdot n = 0 \\ \したがって\\（1 + e）（（V ^ B-V ^ A）\ cdot n）+ j *（\ frac {j * n} {mass ^ A} + \ frac {j * n} {mass ^ B}）* n = 0 \\ \したがって\\ j = \ frac {-（1 + e）（（V ^ B-V ^ A）\ cdot n）} {\ frac {1} {mass ^ A} + \ frac {1} {mass ^ B}}$$

うわー、非常に多くのコンピューティング！ しかし、それだけです。 左側の式10の最終形では、 $$$j$ （値）、および右側のすべてがすでに認識されています。 これは、数行のコードを記述してスカラーの運動量力を計算できることを意味します $$$j$ 。 そして、このコードは数学表記よりもはるかに読みやすいです！

 void ResolveCollision( Object A, Object B ) { //    Vec2 rv = B.velocity - A.velocity //       float velAlongNormal = DotProduct( rv, normal ) //   ,    if(velAlongNormal > 0) return; //   float e = min( A.restitution, B.restitution) //     float j = -(1 + e) * velAlongNormal j /= 1 / A.mass + 1 / B.mass //    Vec2 impulse = j * normal A.velocity -= 1 / A.mass * impulse B.velocity += 1 / B.mass * impulse } 

このコード例には2つの重要な側面があります。 最初に、 if(VelAlongNormal > 0) 、10行目を見てください。 このチェックは非常に重要です。オブジェクトが互いに向かって移動する場合にのみ衝突を許可します。


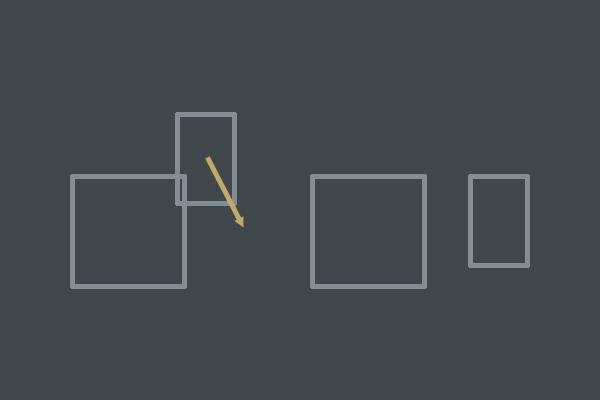2つのオブジェクトが衝突しましたが、速度が次のフレームでそれらを分離します。 このタイプの衝突は許可されません。

オブジェクトが互いに反対方向に移動する場合、何もしません。 このため、実際に衝突しないオブジェクトの衝突は解決しません。 これは、オブジェクトが相互作用するときに何が起こるかについての直感的な期待を満たすシミュレーションを作成するために重要です。

第二に、逆質量が何の理由もなく計算されることは注目に値します。 各オブジェクト内に逆質量を保持し、同時に事前計算するのが最善です。

 A.inv_mass = 1 / A.mass 

多くの物理エンジンでは、未処理の質量は実際には保存されません。 多くの場合、物理エンジンは質量の逆数のみを保存します。 ほとんどの数学的計算では、 1/形式の質量が使用されます。

最後に注意すべきことは、スカラーの勢いをインテリジェントに分散させる必要があるということです。 $$$j$ 2つのオブジェクトに。 大きなオブジェクトから大きなオブジェクトから小さなオブジェクトを飛び去らせたい $$$j$ 、大きなオブジェクトの速度はごくわずかな割合で変化します $$$j$ 。

これを行うには、次のことを実行できます。

 float mass_sum = A.mass + B.mass float ratio = A.mass / mass_sum A.velocity -= ratio * impulse ratio = B.mass / mass_sum B.velocity += ratio * impulse 

このコードは上記のResolveCollision()関数の例に似ていることに注意することが重要です。 上で説明したように、バックマスは物理エンジンで非常に役立ちます。

沈没物

すでに記述されたコードを使用すると、オブジェクトは衝突し、互いに飛び去ります。 これは素晴らしいことですが、オブジェクトの1つに無限の質量がある場合はどうなりますか？ シミュレーションで無限質量を定義する便利な方法が必要になります。

無限質量としてゼロを使用することをお勧めします-ただし、質量がゼロのオブジェクトの逆質量を計算しようとすると、ゼロで除算されます。 相互質量の計算におけるこの問題の解決策は次のとおりです。

 if(A.mass == 0) A.inv_mass = 0 else A.inv_mass = 1 / A.mass 

「ゼロ」の値は、力パルスを解決するときに正しい計算につながります。 それは私たちに合っています。 オブジェクトが沈む問題は、あるオブジェクトが重力によって別のオブジェクトに「沈み始める」ときに発生します。 低弾性の物体が無限の質量の壁にぶつかり、沈み始めることがあります。

このdrれは、浮動小数点計算エラーが原因で発生します。 各浮動小数点の計算中に、ハードウェアの制限により小さなエラーが追加されます。 （詳細については、Googleの[浮動小数点エラーIEEE754]を参照してください。）時間が経つにつれて、このエラーはポジショニングエラーに蓄積され、相互にオブジェクトがownれてしまいます。

この位置決め誤差を修正するには、それを考慮する必要があるため、「線形投影」と呼ばれる方法を紹介します。 わずかな割合での線形投影により、2つのオブジェクトの相互への浸透が減少します。 力インパルスの適用後に実行されます。 位置の修正は非常に簡単です：各オブジェクトを法線に沿って衝突に移動します $$$n$ 浸透率による：

 void PositionalCorrection( Object A, Object B ) { const float percent = 0.2 //   20%  80% Vec2 correction = penetrationDepth / (A.inv_mass + B.inv_mass)) * percent * n A.position -= A.inv_mass * correction B.position += B.inv_mass * correction } 

penetrationDepthをシステムの総質量にスケーリングpenetrationDepthことに注意してください。 これにより、質量に比例した位置補正が行われます。 小さなオブジェクトは重いオブジェクトよりも速く反発します。

ただし、この実装には小さな問題があります。位置決めエラーを常に解決する場合、オブジェクトは互いの上にある間、常に震えます。 ジッタを除去するには、小さな許容値を設定する必要があります。 侵入が特定の任意のしきい値を超える場合にのみ修正を実行します。これを「スロップ」と呼びます。

 void PositionalCorrection( Object A, Object B ) { const float percent = 0.2 //   20%  80% const float slop = 0.01 //   0.01  0.1 Vec2 correction = max( penetration - k_slop, 0.0f ) / (A.inv_mass + B.inv_mass)) * percent * n A.position -= A.inv_mass * correction B.position += B.inv_mass * correction } 

これにより、位置補正を行わずにオブジェクトが互いに少し貫通することができます。

---

単純な品種の生成

この記事のこの部分で最後に検討するのは、単純な多様体の生成です。 数学の多様性は、「空間の領域を表す点の集合」のようなものです。 ただし、ここでは「多様性」とは、2つのオブジェクト間の衝突に関する情報を含む小さなオブジェクトを意味します。

標準的な多様体宣言は次のようになります。

 struct Manifold { Object *A; Object *B; float penetration; Vec2 normal; }; 

衝突検出中に、侵入と衝突法線を計算する必要があります。 この情報を決定するには、記事の最初から元の衝突認識アルゴリズムを拡張する必要があります。

サークルサークル

最も単純なコリジョンアルゴリズム、サークルサークルコリジョンから始めましょう。 このチェックはもっと簡単です。 紛争解決の方向性を想像できますか？ これは、円Aから円Bへのベクトルです。位置Aから位置Bを引くことで取得できます。

侵入の深さは、円の半径と円の間の距離に関連しています。 円の面付けは、各オブジェクトまでの距離の半径の合計から減算することで計算できます。

次に、円間衝突多様体生成アルゴリズムの完全な例を示します。

 bool CirclevsCircle( Manifold *m ) { //       Object *A = m->A; Object *B = m->B; //   A  B Vec2 n = B->pos - A->pos float r = A->radius + B->radius r *= r if(n.LengthSquared( ) > r) return false //    ,   float d = n.Length( ) //  sqrt //        if(d != 0) { //  -       m->penetration = r - d //  d,      sqrt  Length( ) //   A  B,     c->normal = t / d return true } //     else { //   ( )  c->penetration = A->radius c->normal = Vec( 1, 0 ) return true } } 

ここでは、次の点に注意する価値があります。平方根計算は実行しませんが、平方根計算なしで実行できます（オブジェクトに衝突がない場合）。円が1点にあるかどうかを確認します。 それらが同じポイントにある場合、距離はゼロになり、 t / d計算するときにゼロで除算しないようにする必要があります。

AABB-AABB

AABB-AABBのテストは、円よりも少し複雑です。 衝突法線は、AからBへのベクトルではなく、エッジの法線になります。 AABBは4つのエッジを持つ長方形です。 各エッジには法線があります。 この法線は、エッジに垂直な単位ベクトルを示します。

2Dの線の一般方程式を調べます。

$$

$$ax + by + c = 0 \\ normal = \ begin {bmatrix} a \\ b \ end {bmatrix}$$

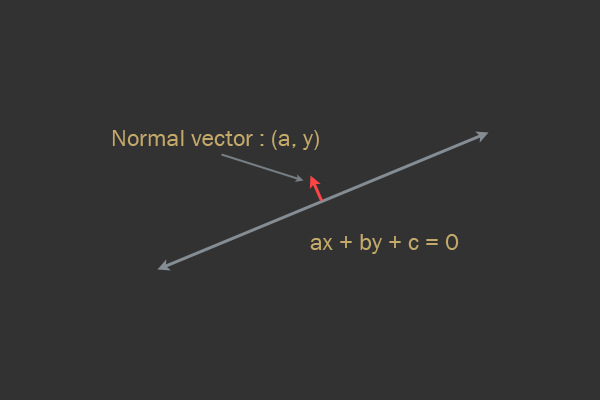
上記の方程式でa 、 bとbはラインの法線ベクトルであり、ベクトル(a, b)は正規化されていると見なされます（ベクトルの長さはゼロです）。 衝突法線（衝突解決の方向）は、法線のエッジの1つに向けられます。

線の一般的な方程式でcが何を表しているか知っていますか？ cは、原点までの距離です。 記事の次の部分で見るように、これはポイントが行のどちら側にあるかを確認するのに非常に便利です。

ここで必要なのは、あるオブジェクトのどのエッジが別のオブジェクトと衝突するかを判断することです。その後、法線を取得します。 ただし、2つの角度が交差する場合など、2つのAABBのいくつかのエッジが交差する場合があります。 これは、最小浸透の軸を決定する必要があることを意味します。


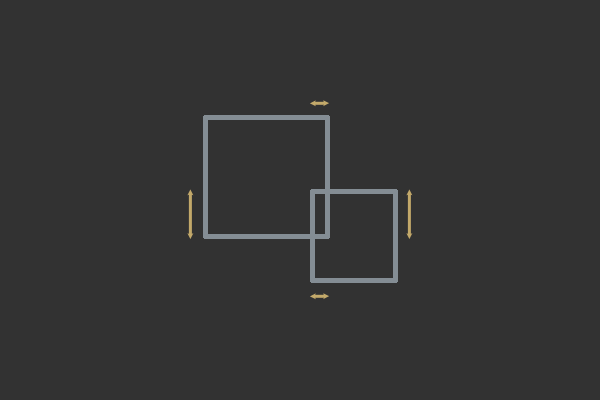貫通の2つの軸。 水平方向のX軸は貫通が最も少ない軸なので、この衝突はX軸に沿って解決する必要があります。

AABB-AABB多様体と衝突認識を生成するための完全なアルゴリズムは次のとおりです。

 bool AABBvsAABB( Manifold *m ) { //        Object *A = m->A Object *B = m->B //   A  B Vec2 n = B->pos - A->pos AABB abox = A->aabb AABB bbox = B->aabb //      x    float a_extent = (abox.max.x - abox.min.x) / 2 float b_extent = (bbox.max.x - bbox.min.x) / 2 //     x float x_overlap = a_extent + b_extent - abs( nx ) //  SAT   x if(x_overlap > 0) { //      y    float a_extent = (abox.max.y - abox.min.y) / 2 float b_extent = (bbox.max.y - bbox.min.y) / 2 //     y float y_overlap = a_extent + b_extent - abs( ny ) //  SAT   y if(y_overlap > 0) { // ,       if(x_overlap > y_overlap) { //    B, ,  n     A  B if(nx < 0) m->normal = Vec2( -1, 0 ) else m->normal = Vec2( 0, 0 ) m->penetration = x_overlap return true } else { //    B, ,  n     A  B if(ny < 0) m->normal = Vec2( 0, -1 ) else m->normal = Vec2( 0, 1 ) m->penetration = y_overlap return true } } } } 

-AABB

最後に検討するテストは、サークルAABBチェックです。ここでのアイデアは、円に最も近いポイントAABBを計算することです。その後、チェックは円と円のチェックのようなものに単純化されます。最も近い点を計算し、衝突を認識した後、法線は円の中心から最も近い点への方向になります。浸透深度は、円に最も近い点までの距離と円の半径の差です。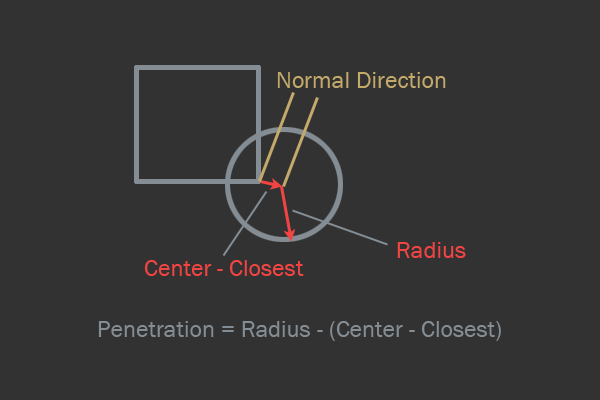


交差点スキームAABBサークル。

トリッキーな特殊なケースが1つあります。円の中心がAABBの内側にある場合は、円の中心をAABBの最も近い端まで切り取り、法線を反映する必要があります。

 bool AABBvsCircle( Manifold *m ) { //        Object *A = m->A Object *B = m->B //   A  B Vec2 n = B->pos - A->pos //    B  A Vec2 closest = n //       float x_extent = (A->aabb.max.x - A->aabb.min.x) / 2 float y_extent = (A->aabb.max.y - A->aabb.min.y) / 2 //    AABB closest.x = Clamp( -x_extent, x_extent, closest.x ) closest.y = Clamp( -y_extent, y_extent, closest.y ) bool inside = false //   AABB,       //    if(n == closest) { inside = true //    if(abs( nx ) > abs( ny )) { //     if(closest.x > 0) closest.x = x_extent else closest.x = -x_extent } //  y  else { //     if(closest.y > 0) closest.y = y_extent else closest.y = -y_extent } } Vec2 normal = n - closest real d = normal.LengthSquared( ) real r = B->radius //   ,       //     AABB if(d > r * r && !inside) return false //  sqrt,      d = sqrt( d ) //     AABB,      //    if(inside) { m->normal = -n m->penetration = r - d } else { m->normal = n m->penetration = r - d } return true } 

---

おわりに

物理シミュレーションについてもう少し理解できたと思います。このチュートリアルは、独自の物理エンジンの作成をゼロから始めるのに十分です。次の部分では、物理エンジンに必要なすべての必要な拡張、つまり以下を検討します。

• コンタクトペアのソートとクリッピング
• 広い位相
• バンドル
• 統合
• バー
• 半空間の交差点
• モジュール性（材料、質量、強度）