ロボットにピザを調理するように教えます。 パート2：ニューラルネットワークの一致

内容

• パート1：データの取得

最後の部分では、ドードーピザのWebサイトを解析し、成分に関するデータをダウンロードしました。最も重要なのは、ピザの写真です。 合計20のピザを自由に使用できました。 もちろん、わずか20枚の画像からトレーニングデータを生成することはできません。 ただし、ピザの軸対称を使用できます。写真を1度ずつ回転させ、垂直に反射させることにより、1枚の写真を720枚の画像のセットに変換できます。 また、十分ではありませんが、それでも試してみてください。

条件付き変分オートエンコーダーをトレーニングしてから、それが何であるか-生成的敵対ネットワーク-に進みましょう。

CVAE-条件付き変分オートエンコーダー

自動エンコーダーの手続きについては、次の優れた記事が役立ちます。

• Keras Auto Encoders、パート3：Variable Variable Auto Encoders（VAE）
• Keras Auto Encoders、パート4：条件付きVAE

読むことを強くお勧めします。
ここでポイントに直行します。

CVAEとVAEの違いは、エンコーダーとデコーダーの両方を入力し、さらに別のラベルを提供する必要があることです。 この場合、ラベルはOneHotEncoderから受け取ったレシピのベクトルになります。

しかし、ニュアンスがあります-そして、どの時点でラベルを提出するのが意味がありますか？

私は2つの方法を試しました：

1. 最後に-すべての畳み込みの後-完全に接続されたレイヤーの前
2. 最初-最初の畳み込みの後-追加のチャネルとして追加されます

原則として、どちらの方法にも存在する権利があります。 ラベルを最後に追加すると、画像の高レベルの機能にラベルが追加されるのは論理的なようです。 また、その逆-最初に追加すると、低レベルの機能に関連付けられます。 両方の方法を比較してみましょう。

レシピは最大9つの材料で構成されていることを思い出してください。 28個ありますが、レシピコードは9x29マトリックスであり、これを拡張すると261次元のベクトルが得られることがわかります。

32x32のサイズの画像の場合、512に等しい隠しスペースのサイズを選択します。
より少ない数を選択することもできますが、後で見られるように、これはよりぼやけた結果につながります。

ラベルを追加する最初の方法を使用したエンコーダーのコードは、すべての畳み込みの後です。

def create_conv_cvae(channels, height, width, code_h, code_w): input_img = Input(shape=(channels, height, width)) input_code = Input(shape=(code_h, code_w)) flatten_code = Flatten()(input_code) latent_dim = 512 m_height, m_width = int(height/4), int(width/4) x = Conv2D(32, (3, 3), activation='relu', padding='same')(input_img) x = MaxPooling2D(pool_size=(2, 2), padding='same')(x) x = Conv2D(16, (3, 3), activation='relu', padding='same')(x) x = MaxPooling2D(pool_size=(2, 2), padding='same')(x) flatten_img_features = Flatten()(x) x = concatenate([flatten_img_features, flatten_code]) x = Dense(1024, activation='relu')(x) z_mean = Dense(latent_dim)(x) z_log_var = Dense(latent_dim)(x) 

ラベルを追加する2番目の方法（最初の畳み込みの後）を追加チャネルとして使用するエンコーダーのコード：

 def create_conv_cvae2(channels, height, width, code_h, code_w): input_img = Input(shape=(channels, height, width)) input_code = Input(shape=(code_h, code_w)) flatten_code = Flatten()(input_code) latent_dim = 512 m_height, m_width = int(height/4), int(width/4) def add_units_to_conv2d(conv2, units): dim1 = K.int_shape(conv2)[2] dim2 = K.int_shape(conv2)[3] dimc = K.int_shape(units)[1] repeat_n = dim1*dim2 count = int( dim1*dim2 / dimc) units_repeat = RepeatVector(count+1)(units) #print('K.int_shape(units_repeat): ', K.int_shape(units_repeat)) units_repeat = Flatten()(units_repeat) # cut only needed lehgth of code units_repeat = Lambda(lambda x: x[:,:dim1*dim2], output_shape=(dim1*dim2,))(units_repeat) units_repeat = Reshape((1, dim1, dim2))(units_repeat) return concatenate([conv2, units_repeat], axis=1) x = Conv2D(32, (3, 3), activation='relu', padding='same')(input_img) x = add_units_to_conv2d(x, flatten_code) #print('K.int_shape(x): ', K.int_shape(x)) # size here: (17, 32, 32) x = MaxPooling2D(pool_size=(2, 2), padding='same')(x) x = Conv2D(16, (3, 3), activation='relu', padding='same')(x) x = MaxPooling2D(pool_size=(2, 2), padding='same')(x) x = Flatten()(x) x = Dense(1024, activation='relu')(x) z_mean = Dense(latent_dim)(x) z_log_var = Dense(latent_dim)(x) 

どちらの場合のデコーダコードも同じです。ラベルは最初に追加されます。

  z = Input(shape=(latent_dim, )) input_code_d = Input(shape=(code_h, code_w)) flatten_code_d = Flatten()(input_code_d) x = concatenate([z, flatten_code_d]) x = Dense(1024)(x) x = Dense(16*m_height*m_width)(x) x = Reshape((16, m_height, m_width))(x) x = Conv2D(16, (3, 3), activation='relu', padding='same')(x) x = UpSampling2D((2, 2))(x) x = Conv2D(32, (3, 3), activation='relu', padding='same')(x) x = UpSampling2D((2, 2))(x) decoded = Conv2D(channels, (3, 3), activation='sigmoid', padding='same')(x) 

ネットワークパラメータの数：

1. 4'221'987
2. 3'954'867

1つの時代の学習速度：

1. 60秒
2. 63秒

研究の40時代後の結果：

1. 損失：-0.3232 val_loss：-0.3164
2. 損失：-0.3245 val_loss：-0.3191

ご覧のとおり、2番目の方法では、ANNのメモリが少なくて済み、より良い結果が得られますが、トレーニングには少し時間がかかります。

結果を視覚的に比較することは残っています。

1. 元の画像（32x32）
2. 作業の結果は最初のメソッドです（latent_dim = 64）
3. 結果は最初のメソッドです（latent_dim = 512）
4. 作業の結果は2番目の方法です（latent_dim = 512）

ここで、ピザが元のレシピでエンコードされ、別のレシピでデコードされる場合、ピザのスタイル転送のアプリケーションがどのように見えるかを見てみましょう。

 i = 0 for label in labels: i += 1 lbls = [] for j in range(batch_size): lbls.append(label) lbls = np.array(lbls, dtype=np.float32) print(i, lbls.shape) stt_imgs = stt.predict([orig_images, orig_labels, lbls], batch_size=batch_size) save_images(stt_imgs, dst='temp/cvae_stt', comment='_'+str(i)) 

スタイル転送の結果（2番目のエンコード方法）：

GAN-生成的敵対ネットワーク

そのようなネットワークの確立されたロシア語の名前を見つけることができませんでした。
オプション：

• 生成的競争ネットワーク
• ライバルネットワークの生成
• 競合するネットの生成

私はそれが好きです：

• 生成的敵対ネットワーク

一連の優れた記事がGANの仕事の理論に役立ちます。

• Keras Auto Encoders、パート5：GAN（Generative Adversarial Networks）およびtensorflow
• Kerasパート6の自動エンコーダー：VAE + GAN

より深く理解するために-ODSの最新ブログ記事： ニューラルネットワークシミュレーションゲーム

しかし、生成ニューラルネットワークを理解し、独立して実装しようとすると、いくつかの困難に直面しました。 例えば、発電機が真にサイケデリックな写真を作成することがありました。

実装の理解に役立つさまざまな例：

ケラスのMNIST生成的敵対モデル （ mnist_gan.py ）、

DCGAN （Deep Convolutional GAN）に関するFacebook調査からの2015年末の記事からのアーキテクチャの推奨事項：

深い畳み込みの生成的敵対ネットワークによる教師なし表現学習

GANを機能させるための一連の推奨事項：

GANをトレーニングする方法は？ GANを機能させるためのヒントとコツ 。

GANデザイン：

 def make_trainable(net, val): net.trainable = val for l in net.layers: l.trainable = val def create_gan(channels, height, width): input_img = Input(shape=(channels, height, width)) m_height, m_width = int(height/8), int(width/8) # generator z = Input(shape=(latent_dim, )) x = Dense(256*m_height*m_width)(z) #x = BatchNormalization()(x) x = Activation('relu')(x) #x = Dropout(0.3)(x) x = Reshape((256, m_height, m_width))(x) x = Conv2DTranspose(256, kernel_size=(5, 5), strides=(2, 2), padding='same', activation='relu')(x) x = Conv2DTranspose(128, kernel_size=(5, 5), strides=(2, 2), padding='same', activation='relu')(x) x = Conv2DTranspose(64, kernel_size=(5, 5), strides=(2, 2), padding='same', activation='relu')(x) x = Conv2D(channels, (5, 5), padding='same')(x) g = Activation('tanh')(x) generator = Model(z, g, name='Generator') # discriminator x = Conv2D(128, (5, 5), padding='same')(input_img) #x = BatchNormalization()(x) x = LeakyReLU()(x) #x = Dropout(0.3)(x) x = MaxPooling2D(pool_size=(2, 2), padding='same')(x) x = Conv2D(256, (5, 5), padding='same')(x) x = LeakyReLU()(x) x = MaxPooling2D(pool_size=(2, 2), padding='same')(x) x = Conv2D(512, (5, 5), padding='same')(x) x = LeakyReLU()(x) x = MaxPooling2D(pool_size=(2, 2), padding='same')(x) x = Flatten()(x) x = Dense(2048)(x) x = LeakyReLU()(x) x = Dense(1)(x) d = Activation('sigmoid')(x) discriminator = Model(input_img, d, name='Discriminator') gan = Sequential() gan.add(generator) make_trainable(discriminator, False) #discriminator.trainable = False gan.add(discriminator) return generator, discriminator, gan gan_gen, gan_ds, gan = create_gan(channels, height, width) gan_gen.summary() gan_ds.summary() gan.summary() opt = Adam(lr=1e-3) gopt = Adam(lr=1e-4) dopt = Adam(lr=1e-4) gan_gen.compile(loss='binary_crossentropy', optimizer=gopt) gan.compile(loss='binary_crossentropy', optimizer=opt) make_trainable(gan_ds, True) gan_ds.compile(loss='binary_crossentropy', optimizer=dopt) 

ご覧のとおり、弁別器は以下を生成する通常のバイナリ分類器です。

1-実際の写真の場合、
0-偽物。

トレーニング手順：

• 実際の写真の一部を取得します
• ノイズを生成し、それに基づいてジェネレーターが画像を生成します
• 実際の画像（ラベル1が割り当てられます）とジェネレーターからの偽物（ラベル0）で構成される弁別器をトレーニングするためのバッチを形成します
• 訓練弁別器
• GANをトレーニングし（判別器トレーニングが無効になっているため、ジェネレーターがトレーニングされます）、入力にノイズを適用し、出力がマーク1になるのを待ちます。

 for epoch in range(epochs): print('Epoch {} from {} ...'.format(epoch, epochs)) n = x_train.shape[0] image_batch = x_train[np.random.randint(0, n, size=batch_size),:,:,:] noise_gen = np.random.uniform(-1, 1, size=[batch_size, latent_dim]) generated_images = gan_gen.predict(noise_gen, batch_size=batch_size) if epoch % 10 == 0: print('Save gens ...') save_images(generated_images) gan_gen.save_weights('temp/gan_gen_weights_'+str(height)+'.h5', True) gan_ds.save_weights('temp/gan_ds_weights_'+str(height)+'.h5', True) # save loss df = pd.DataFrame( {'d_loss': d_loss, 'g_loss': g_loss} ) df.to_csv('temp/gan_loss.csv', index=False) x_train2 = np.concatenate( (image_batch, generated_images) ) y_tr2 = np.zeros( [2*batch_size, 1] ) y_tr2[:batch_size] = 1 d_history = gan_ds.train_on_batch(x_train2, y_tr2) print('d:', d_history) d_loss.append( d_history ) noise_gen = np.random.uniform(-1, 1, size=[batch_size, latent_dim]) g_history = gan.train_on_batch(noise_gen, np.ones([batch_size, 1])) print('g:', g_history) g_loss.append( g_history ) 

バリエーション自動エンコーダーとは異なり、ジェネレーターのトレーニングには実画像は使用されず、弁別器ラベルのみが使用されることに注意してください。 すなわち 発生器は、弁別器からの誤差勾配で訓練されます。

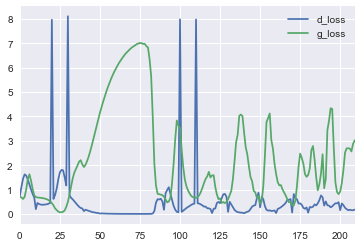
最も興味深いのは、敵対的なネットワークという名前はいい言葉ではないということです。彼らは本当に競争しており、弁別器と発電機の損失の測定値を追跡するのも楽しいです。

損失曲線を見ると、弁別器はジェネレーターによって生成された元のゴミと実際の画像を区別することをすぐに学習しますが、曲線は振動し始めます-ジェネレーターは、ますます適切な画像を生成することを学習します。

1つのピザ（リストの最初のピザはダブルペパロニ）のジェネレーター（32x32）の学習プロセスを示すgif：

予想どおり、GANの結果は、変分エンコーダーと比較して、より鮮明な画像を提供します。

CVAE + GAN-条件付き変分オートエンコーダーおよび生成的敵対ネットワーク

CVAEとGANを組み合わせて、両方のネットワークを最大限に活用します。 ユニオンの基本はシンプルなアイデアです-VAEデコーダーはGANジェネレーターとまったく同じ機能を実行しますが、異なる方法で実行および学習します。

このすべてを一緒に機能させる方法が完全に明確ではなかったという事実に加えて、Kerasでさまざまな損失関数をどのように使用できるかについても明確ではありませんでした。 この問題の検索は、githubの例によって助けられました。

→ Keras VAEおよびGAN

そのため、Kerasのさまざまな損失関数のアプリケーションは、独自のレイヤー（ 独自のKerasレイヤーを記述する）をcall（）メソッドに追加することで実装できます.call（）メソッドでは、必要な計算ロジックをadd_loss（）メソッドへの後続の呼び出しで実装できます。

例：

 class DiscriminatorLossLayer(Layer): __name__ = 'discriminator_loss_layer' def __init__(self, **kwargs): self.is_placeholder = True super(DiscriminatorLossLayer, self).__init__(**kwargs) def lossfun(self, y_real, y_fake_f, y_fake_p): y_pos = K.ones_like(y_real) y_neg = K.zeros_like(y_real) loss_real = keras.metrics.binary_crossentropy(y_pos, y_real) loss_fake_f = keras.metrics.binary_crossentropy(y_neg, y_fake_f) loss_fake_p = keras.metrics.binary_crossentropy(y_neg, y_fake_p) return K.mean(loss_real + loss_fake_f + loss_fake_p) def call(self, inputs): y_real = inputs[0] y_fake_f = inputs[1] y_fake_p = inputs[2] loss = self.lossfun(y_real, y_fake_f, y_fake_p) self.add_loss(loss, inputs=inputs) return y_real 

学習プロセス（64x64）を示すgif：

スタイル移転作業の結果：

そして今、楽しい部分です！

実際には、それがすべてだったもののために-選択した食材のためのピザの世代。

1つの成分からなるレシピ（つまり、1〜27のコード）でピザを見てみましょう。

予想されるように-最も人気のある成分24、20、17（トマト、ペパロニ、モッツァレラ）を含むピザのみが多かれ少なかれ見える-他のすべてのオプションは、丸い形とあいまいな灰色の斑点があり、必要な場合のみあなたは何かを推測しようとすることができます。

おわりに

一般に、実験は部分的に成功したとみなすことができます。 しかし、このようなおもちゃの例でも、「データは新しいオイルです」という哀pathの表現には、特に機械学習に関して存在する権利があると感じることができます。
結局のところ、機械学習に基づくアプリケーションの品質は、主にデータの品質と量に依存します。

ジェネレーティブネットワークは非常に興味深いものであり、近い将来、それらのアプリケーションの多くの異なる例が見られると思います。

ところで、写真に対する権利がその作成者のものである場合、ニューラルネットワークが作成する画像に対する権利は誰が所有しているのでしょうか？

ご清聴ありがとうございました！

NB。 この記事を書いているとき、ピザは1つもヒットしていません。

参照資料

• Keras Auto Encoders、パート3：Variable Variable Auto Encoders（VAE）
• Keras Auto Encoders、パート4：条件付きVAE
• Keras Auto Encoders、パート5：GAN（Generative Adversarial Networks）およびtensorflow
• Kerasパート6の自動エンコーダー：VAE + GAN
• ディープコンボリューショナルGAN（DCGAN）：ディープコンボリューショナル生成的敵対ネットワークによる教師なし表現学習
• GANをトレーニングする方法は？ GANを機能させるためのヒントとコツ
• Keras VAEおよびGAN
• KerasのMNIST生成的敵対モデル （ mnist_gan.py ）
• 生成的敵対ネットワークパート2-Keras 2.0による実装
• Kerasによる生成的敵対ネットワーク
• TensorflowバックエンドでKerasを使用したGANの例
• Deep Convolutional Generative Adversarial Networks（DCGAN）のKeras実装
• OpenAIの生成モデル
• ニューラルネットワークシミュレーションゲーム