🛅 🤒 👂🏾 データジオメトリ3.ペアのスカラー積 👨🏻‍💻 👼🏼 🖐️

要素間の距離の不変量（距離の2乗）は、要素の差をそれ自体ではなく、要素の別の差で乗算すると一般化できます。結果の値は、順序付けられたペアのスカラー積を反映します。

1.シンプレックスとグラフ
2. 2座標および2座標の決定
3.ペアのスカラー積
4.グラフのスペース
5.基底変換
6.星を数える

注文したペア

ベクトルの座標は、要素の座標間の差として取得できますが、逆は当てはまりません。ベクトルの座標からそれを形成する要素の座標を復元することは不可能です。 2つの要素の座標には、ベクトルの座標よりも多くの情報が含まれています。したがって、要素からペアを形成できます-ベクトルの改良された類似体。このような2つの要素のセットは、順序付きペアと呼ばれます。

順序付けられた各ペアは、ベクトル（ペアを形成する要素の差）に関連付けることができます。 2つのベクトルの場合、スカラー積を定義できます。これは、空間の4つの要素の特性と見なすこともできます。

スカラー積

この部分のかさばりを減らすために、小文字の要素を指定します。ペアは、2つの要素の組み合わせです。

（ i 、 j ）

$（i、j）$ 。ペアに対応するベクトルは、ペアの要素の差です。

m a t h b f v_{i j} = j - i q u a d （ 3.1 ）

$\ mathbf {v} _ {ij} = j-i \ quad（3.1）$

要素のノルムは、それ自体とのスカラー積です。

n_{i} = i c d o t i q u a d （ 3.2 ）

$n_i = i \ cdot i \ quad（3.2）$

同じ定義をペアのベクトルに使用できます。これは、ご存じのとおり、ペアの要素間の距離の2乗を反映しています。

q_{i j} e q u i v n_{i j} = （ j - i ） c d o t （ j - i ） q u a d （ 3.3 ）

$q_ {ij} \ equiv n_ {ij} =（j-i）\ cdot（j-i）\ quad（3.3）$

2つの異なるペアが指定されている場合

（ i 、 j ）

$（i、j）$ そして

（ k 、 l ）

$（k、l）$ 、その後、対応するベクトル間のスカラー積を決定できます。

g_{i j 、 k l} = （ j - i ） c d o t （ l - k ） = m a t h b f v_{i j} c d o t m a t h b f v_{k l} q u a d （ 3.4 ）

$g_ {ij、kl} =（j-i）\ cdot（l-k）= \ mathbf {v} _ {ij} \ cdot \ mathbf {v} _ {kl} \ quad（3.4）$

指数

i j

$ij$ 1つのペアとインデックスを設定します

k l

$kl$ -別の。

式（3.4）は、4つの要素の相対位置に応じてスカラーを定義します。このスカラーは、要素間の距離で表現できることが重要です

q_{i j}

$q_ {ij}$ 。

ご存知のように、要素間の距離は、要素間のスカラー積に関連付けられています。

q_{i j} = n_{i} - 2 g_{i j} + n_{j} q u a d （ 3.5 ）

$q_ {ij} = n_i-2 g_ {ij} + n_j \ quad（3.5）$ 。

（3.5）を考慮して製品（3.4）を開くと、以下が得られます。

g_{i j 、 k l} = （ q_{i l} + q_{j k} - q_{i k} - q_{j l} ） / 2 q u a d （ 3.6 ）

$g_ {ij、kl} =（q_ {il} + q_ {jk}-q_ {ik}-q_ {jl}）/ 2 \ quad（3.6）$

これは、ペアのスカラー積の一般式です。インデックスの順序は重要です—対応するベクトルのペアと方向を設定します。

（3.6）のような表現は、数学のさまざまな場所でしばしば発生します。これは、この公式の結論の一般性によるものです。代数式の最も一般的なプロパティのみを使用したことに注意してください。したがって、製品操作が定義されているオブジェクトを要素として使用できます。アイデンティティは彼らにとって真実であり、一般的な形では次のようになります。

（ A - B ） c d o t （ C - D ） = （ （ A - D ）^{2} + （ B - C ）^{2} - （ A - C ）^{2} - （ B - D ）^{2} ） / 2 q u a d （ 3.6.1 ）

$（A-B）\ cdot（C-D）=（（A-D）^ 2 +（B-C）^ 2-（A-C）^ 2-（B-D）^ 2）/ 2 \ quad（3.6.1）$

共通のトップとのペア-隣接ペア

ペアに共通の頂点がある場合

（ k e q u i v l ）

$（k \ equiv l）$ 、次に式（3.6）が簡略化されます。

g_{k i 、 k j} = （ q_{i k} + q_{j k} - q_{i j} ） / 2 q u a d （ 3.7 ）

$g_ {ki、kj} =（q_ {ik} + q_ {jk}-q_ {ij}）/ 2 \ quad（3.7）$

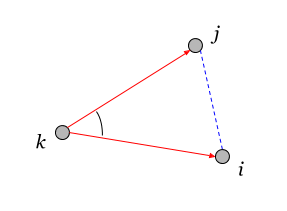
式（3.7）は、三角形の余弦定理です。ここで、相互ノルムが決定されるペアは、共通の要素k- 隣接ペアを持ちます。

3つの頂点で、3つのスカラー積を定義できます。それらの合計は、頂点間の距離の合計で表されます。

g_{k i 、 k j} + g_{i k 、 i j} + g_{j i 、 j k} = （ q_{j k} + q_{i k} + q_{i j} ） / 2 q u a d （ 3.8.1 ）

$g_ {ki、kj} + g_ {ik、ij} + g_ {ji、jk} =（q_ {jk} + q_ {ik} + q_ {ij}）/ 2 \ quad（3.8.1）$

3つの頂点でのスカラー積の正方形は、それらによって形成される三角形の面積と接続されます

s_{i j k}

$s_ {ijk}$ （ヘロンの式）：

4 s_{i j k}^{2} = q_{i k} q_{j k} - （ g_{i k 、 j k} ）^{2} q u a d （ 3.8.2 ）

$4 s_ {ijk} ^ 2 = q_ {ik} q_ {jk}-（g_ {ik、jk}）^ 2 \ quad（3.8.2）$

独立したカップル-4つの異なるピーク

一般的な場合、ペアの頂点は同じ平面にない場合があります。したがって、スカラー積の定義を考えると、方向間の角度の余弦を一致させることが常に可能とは限りません。

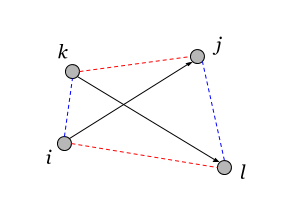
スカラー積のプロパティをリストします（3.6）。

1）ペアの順列に依存しません：

g_{i j 、 k l} = g_{k l 、 i j} q u a d （ 3.9.1 ）

$g_ {ij、kl} = g_ {kl、ij} \ quad（3.9.1）$

2）ペアの要素の順列に対して非対称

i j

$ij$ または

k l

$kl$ ：

g_{i j 、 k l} = - g_{j i 、 k l} = - g_{i j 、 l k} q u a d （ 3.9.2 ）

$g_ {ij、kl} = -g_ {ji、kl} = -g_ {ij、lk} \ quad（3.9.2）$

3）4つの要素の場合、同一性によるペアの独立したスカラー積は2つのみです。

g_{i j 、 k l} + g_{i k 、 l j} + g_{i l 、 j k} = 0 q u a d （ 3.9.3 ）

$g_ {ij、kl} + g_ {ik、lj} + g_ {il、jk} = 0 \ quad（3.9.3）$

数学者は、式（3.9.3）で最初のビアンキ恒等式を見ます。このことから、曲率テンソル（リーマン）の構造とペアのスカラー積は類似していると結論付けることができます。

4）独立ペアのノルムは、隣接ペアのノルムの差で表現できます。

g_{i j 、 k l} = g_{i j 、 i l} - g_{i j 、 i k} q u a d （ 3.9.4 ）

$g_ {ij、kl} = g_ {ij、il}-g_ {ij、ik} \ quad（3.9.4）$

このIDは次の記事で使用します。

5）要素間の距離

i

$i$ そして

j

$j$ は、隣接する独立したペアのスカラー積で表現できます。

q_{i j} = g_{i j 、 i k} - g_{i j 、 j k} = g_{i l 、 i k} + g_{j l 、 j k} - g_{i l 、 j k} - g_{j l 、 i k} q u a d （ 3.9.5 ）

$q_ {ij} = g_ {ij、ik}-g_ {ij、jk} = g_ {il、ik} + g_ {jl、jk}-g_ {il、jk}-g_ {jl、ik} \ quad（ 3.9.5）$

基本要素のペア

ペアを構成する要素として、基底の頂点を選択できます。次に、ペアのスカラー積がテンソルになります-与えられた基底の要素のすべての可能なペア間のスカラー積のセット。テンソルとスカラーを区別するために、最初のテンソルに大文字を使用します。つまり、スカラーの代わりに

g_{i j 、 k l}

$g_ {ij、kl}$ 基底要素については、テンソルを取得します

G_{i j 、 k l}

$G_ {ij、kl}$ 。

ラプラシアンのスカラー積と補因子

基底要素によって形成されるペアのスカラー積は、基底のラプラシアンの特性に関して表現できます。

2組の頂点が与えられた場合

（ i 、 j ）

$（i、j）$ そして

（ k 、 l ）

$（k、l）$ 、そのスカラー積の値は、2次補因子を除算することにより取得できます

U_{i j 、 k l} （ L ）

$U_ {ij、kl}（L）$ ラプラシアンのスカラーポテンシャルについて

u （ L ）

$u（L）$ ：

G_{i j 、 k l} = U_{i j 、 k l} （ L ） / u （ L ） q u a d （ 3.10.1 ）

$G_ {ij、kl} = U_ {ij、kl}（L）/ u（L）\ quad（3.10.1）$

コファクター

U_{i j 、 k l}

$U_ {ij、kl}$ （符号を考慮して）正方行列のマイナーの行列式と呼ばれます。スカラーポテンシャル

u （ L ）

$u（L）$ ラプラシアンの1次補因子です（最初の記事の（1.12）を参照）。

したがって、1つのベクトルに対応する列をラプラシアン行列から削除する必要があります（式では、

i 、 j

$i、j$ 列）、および別の行に対応する行（

k 、 l

$k、l$ ）、結果のマイナーの行列式をスカラーポテンシャルに分割します

u （ L ） = d e t^{'} （ L ）

$u（L）= det '（L）$ 。ラプラシアンの削除された列と行が同じ場合、ノード間の距離の値を取得します。

グラフ上のペアのスカラー積

グラフの頂点のペア間で、それらの相互ノルム（スカラー積）を決定できます。グラフは通常ラプラシアンによって与えられるため、計算には式（3.10.1）を使用できます。

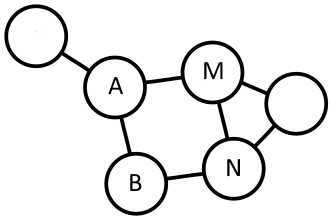
たとえば、2つのペアの生成頂点として選択します。

A 、 B

$A、B$ そして

M 、 N

$M、N$ 。次に、これらのペア間のスカラー積は式（3.6）で与えられます。

G_{A B 、 M N} = （ Q_{A N} + Q_{B M} - Q_{A M} - Q_{B N} ） / 2

$G_ {AB、MN} =（Q_ {AN} + Q_ {BM}-Q_ {AM}-Q_ {BN}）/ 2$

電気回路を表すグラフの場合、スカラー積の値は、電気回路の一般化抵抗の概念を反映しています。この（「見かけの」）抵抗を測定するには、電流源（電圧）を一方のノード（ AおよびB ）に印加し、もう一方（ MおよびN ）間の電位差を測定します。外部電位差が測定されたペアの電位差につながらない場合、ペアの相互ノルム（スカラー積）はゼロに等しくなります。

グラフは離散的である必要はありません-土壌は、選択された要素間のスカラー積を測定することができる連続（連続）グラフの例です。

抵抗法による研究用の設置図：AおよびB-電源の接地。 MおよびN-接地の測定。 1-測定装置（「電気探査」の本、ヤクボブスキーユ。B.、M.、1980年より）。

図は、ペアのスカラー積の測定スキームを示しています

（ A 、 B ）

$（A、B）$ そして

（ M 、 N ）

$（M、N）$ 地面に。

次の記事では、ノードの電位の与えられた測定差と測定された差の比がペアのスカラー積に関連することが判明した理由をより詳しく調べます。

マイナーラプラシアンの変換

対の相互ノルム（スカラー積）の値の部分行列は、ラプラシアンのマイナーを逆にすることによって取得できます。ラプラシアンを表す

a

$a$ 番目の行と

b

$b$ 番目の列のような

L^{i （ a ） 、 j （ b ）}

$L ^ {i（a）、j（b）}$ 。次に、アイデンティティが保持されます。

G_{j b 、 i a} = （ L^{i （ a ） 、 j （ b ）} ）^{- 1} q u a d （ 3.10.2 ）

$G_ {jb、ia} =（L ^ {i（a）、j（b）}）^ {-1} \ quad（3.10.2）$

マトリックスで

G_{j b 、 i a}

$G_ {jb、ia}$ 欠席している

b

$b$ 番目の行と

a

$a$ 番目の列。

ペアのスカラー積の行列が既知の場合

G_{j b 、 i a}

$G_ {jb、ia}$ 、その後、リモートマトリックスを復元できます

Q_{i j}

$Q_ {ij}$ 距離変換に基づきます。最初にサブマトリックスを展開します

G_{j b 、 i a}

$G_ {jb、ia}$ 行がありません

b

$b$ と列

a

$a$ 値がゼロ。結果のマトリックスに、距離変換を適用します。

D i s t_{i j} （ X ） = X_{i i} + X_{j j} - X_{i j} - X_{j i}

$Dist_ {ij}（X）= X_ {ii} + X_ {jj}-X_ {ij}-X_ {ji}$

私たちの場合、アイデンティティ（3.9.5）の形式を取ります。

Q_{i j} = G_{i b 、 i a} + G_{j b 、 j a} - G_{i b 、 j a} - G_{j b 、 i a} q u a d （ 3.10.3 ）

$Q_ {ij} = G_ {ib、ia} + G_ {jb、ja}-G_ {ib、ja}-G_ {jb、ia} \ quad（3.10.3）$

式（3.10.2）と（3.10.3）の組み合わせは、特定のラプラシアンから距離行列を取得する方法の1つです。ラプラシアンからノードの1つを削除します（

a

$a$ ）と描画します。ペアのスカラー積の行列を取得します

G_{i a 、 j a}

$G_ {ia、ja}$ （他の名前は基本的なマトリックスです。次の部分を参照してください）。インデックス値

a

$a$ 固定-ベース頂点。マトリックス内

G_{i a 、 j a}

$G_ {ia、ja}$ ペアの最初の頂点はベースノードにあります

a

$a$ 、2番目は基底の残りの頂点を通り抜けます。

次に、行列に適用します

G_{i a 、 j a}

$G_ {ia、ja}$ 距離変換（3.10.3）。

スカラー積の平方、ヤコビ行列

グラフでエッジ（ラプラシアンの要素）の導電率の値を変更すると、頂点間のすべての距離も変更されることは明らかです（ベクトルのノルム）

Q_{i j}

$Q_ {ij}$ 。導電率が増加すると、距離は減少します（減少します）。神の贈り物は、距離の変化を定性的にだけでなく定量的にも評価できることです。ラプラシアンに関する距離行列の導関数を

Y_{i j 、 k l} = \部 分 的 な Q_{i j} / \部 分 的 な L^{k l} q u a d （ 3.11.1 ）

$Y_ {ij、kl} = \部分的なQ_ {ij} / \部分的なL ^ {kl} \ quad（3.11.1）$

テンソル

Y_{i j 、 k l}

$Y_ {ij、kl}$ ヤコビ行列、つまり距離行列の値の変化の表現

Q_{i j}

$Q_ {ij}$ ラプラシアンの値を変更するとき

L^{k l}

$L ^ {kl}$ 。このテンソルは、ペアのスカラー積の2乗で表されることがわかります。

Y_{i j 、 k l} = （ G_{i j 、 k l} ）^{2} = （ Q_{i l} + Q_{j k} - Q_{i k} - Q_{j l} ）^{2} / 4 q u a d （ 3.11.2 ）

$Y_ {ij、kl} =（G_ {ij、kl}）^ 2 =（Q_ {il} + Q_ {jk}-Q_ {ik}-Q_ {jl}）^ 2/4 \ quad（3.11.2 ）$

つまり、ノードの接続の大きさの変化

i 、 j

$i、j$ ノード間の距離の変化につながる

k 、 l

$k、l$ ペアのスカラー積に比例

（ i 、 j ）

$（i、j）$ そして

（ l 、 k ）

$（l、k）$ 。

頂点の四重テンソル

スカラー積平方テンソル

Y_{i j 、 k l}

$Y_ {ij、kl}$ リバーシブル。式（3.11）を次の同等の形式で表します。

p a r t i a l Q_{i j} = Y_{i j 、 k l} s p a c e p a r t i a l L^{k l} q u a d （ 3.11.3 ）

$\ partial Q_ {ij} = Y_ {ij、kl} \ space \ partial L ^ {kl} \ quad（3.11.3）$

この式は応答として解釈できます。

\部 分 的 な Q_{i j}

$\部分的なQ_ {ij}$ 衝撃で

\部 分 的 な L^{k l}

$\部分的なL ^ {kl}$ 。テンソル

Y_{i j 、 k l}

$Y_ {ij、kl}$ 伝達関数の役割を果たします（露出への応答）。

影響と対応が逆転する逆の状況も可能です。順方向と逆方向

Y^{i j 、 k l}

$Y ^ {ij、kl}$ 伝達関数は比率で関連付けられます。

Y_{i j 、 k l} Y^{k l 、 m n} = d e l t a_{i j}^{m n} q u a d （ 3.12 ）

$Y_ {ij、kl} Y ^ {kl、mn} = \ delta_ {ij} ^ {mn} \ quad（3.12）$

グッドラックアゲイン-テンソル

Y^{i j 、 k l}

$Y ^ {ij、kl}$ ラプラシアンで表現できます：

Y^{i j 、 k l} = \部 分 的 な L^{i j} / \部 分 的 な Q_{k l} = （ L^{i l} L^{j k} + L^{i k} L^{j l} ） / 2 \ク ワ ッ ド （ 3.13 ）

$Y ^ {ij、kl} = \部分的なL ^ {ij} / \部分的なQ_ {kl} =（L ^ {il} L ^ {jk} + L ^ {ik} L ^ {jl}）/ 2 \クワッド（3.13）$

テンソル値

Y^{i j 、 k l}

$Y ^ {ij、kl}$ クワッド接続を呼び出します。

二次テンソルのプロパティ

テンソル値は、4つの頂点のラプラシアンの値によって決定されます。これらの頂点をグラフの頂点と見なします。 4つの頂点がすべて異なると仮定します。

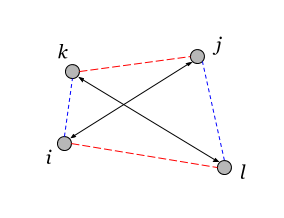
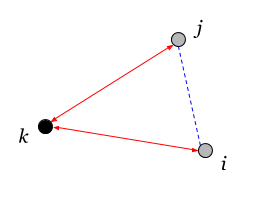
ここで、ベクトルは、2次接続性が考慮される頂点のペアを示します。ペアは、頂点がペアワイズ接続されている場合にのみ、非ゼロのquadconnectednessを持ちます（必要な接続は図で同じ色で示されています）。グラフ内のすべての接続が正の場合、異なる頂点間のクワッド接続も常にゼロ以上になります。

ペアに共通の頂点がある場合、クワッド接続の意味が変更されます。これは、ラプラシアンの対角要素が（距離行列のように）ゼロに等しくないが、ノードの一般的な接続性（導電率）を反映しているという事実によるものです。

Y^{k i 、 k j} = （ L^{k i} L^{k j} + L^{k k} L^{i j} ） / 2 q u a d （ 3.13.1 ）

$Y ^ {ki、kj} =（L ^ {ki} L ^ {kj} + L ^ {kk} L ^ {ij}）/ 2 \ quad（3.13.1）$

頂点のペアは一致する場合があります-二次接続テンソルの対角要素。

Y^{i j} = Q^{i j 、 i j} = （ L^{i i} L^{j j} + （ L^{i j} ）^{2} ） / 2 q u a d （ 3.13.2 ）

$Y ^ {ij} = Q ^ {ij、ij} =（L ^ {ii} L ^ {jj} +（L ^ {ij}）^ 2）/ 2 \ quad（3.13.2）$

ここに

Y^{i j}

$Y ^ {ij}$ 2つのノードiとjの接続を特徴付けます。これは、それらの総伝導率（頂点の程度）の積の合計と見なされます

L^{i i} L^{j j}

$L ^ {ii} L ^ {jj}$ ノード間の接続の二乗

（ L^{i j} ）^{2}

$（L ^ {ij}）^ 2$ 。

正式にテンソルのためにという事実にもかかわらず

Y^{i j 、 k l}

$Y ^ {ij、kl}$ フォームの要素を計算できます

Y^{i j 、 l l}

$Y ^ {ij、ll}$ （ペアの1つが縮退している）、これらの（縮退した）要素は線形に残りに依存しています。これらは、ペアのインデックスの1つを使用してテンソルの合計から計算できます。

Y^{i j 、 l l} = - Y^{i j 、 k l} 1_{k} q u a d （ 3.13.3 ）

$Y ^ {ij、ll} = -Y ^ {ij、kl} 1_k \ quad（3.13.3）$

___
まとめると。すべての点で有用な要素のペアのスカラー積の概念が考慮されます。次の記事では、グラフの部分空間を操作します-それが何であり、そのプロパティが何であるか。

データジオメトリ3.ペアのスカラー積

注文したペア

スカラー積

共通のトップとのペア-隣接ペア

独立したカップル-4つの異なるピーク

基本要素のペア

ラプラシアンのスカラー積と補因子

グラフ上のペアのスカラー積

マイナーラプラシアンの変換

スカラー積の平方、ヤコビ行列

頂点の四重テンソル

二次テンソルのプロパティ

More articles: