カスタムクラスタリング4：自己組織化マップ、微妙さ、改善、t-SNEとの比較

パート1-アフィニティ伝播
パート2-DBSCAN
パート3-時系列クラスタリング
パート4-自己組織化マップ（SOM）
パート5-成長中の神経ガス（GNG）

自己組織化マップ（SOM、Kohonen自己組織化マップ）はおなじみの古典的なデザインです。 彼らは、機械学習コースでソースを覚えていることがよくあります。「そして、ニューラルネットワークはそのようにできます」。 SOMは、1990年から2000年の離陸を生き延びました。その後、彼らは素晴らしい未来を予測し、新しい修正を作成しました。 ただし、21世紀には、SOMは徐々に背景に向かっています。 自己組織化マップの分野での新しい開発はまだ進行中ですが（主にフィンランドのコホネンの発祥地）、地図データのネイティブな視覚化とクラスタリングの分野でも、コホネンはt-SNEよりも劣っています。

SOMの複雑さを理解し、それらが当然忘れられているかどうかを調べてみましょう。

アルゴリズムの重要なアイデア

手短に言えば、標準のSOM学習アルゴリズムを思い出します[1]。 以下 $$$X$（ $$$d \回N$）入力データを含む行列です。ここで、 $$$N$-データセット内の要素の数、および $$$d$-データディメンション。 $$$W$-重みの行列（ $$$d \回M$）、ここで $$$M$-マップ内のニューロンの数。 $$$\ eta$-学習速度、 $$$\シグマ$-協力係数（下記参照）、 $$$E$-時代の数。

$$$D$（ $$$M \回M$）は、レイヤー内のニューロン間の距離のマトリックスです。 最後の行列は次と同じではないことに注意してください $$$\左\ | \ vec {w_i}-\ vec {w_j} \右\ |$。 ニューロンには2つの距離があります ：レイヤー内の距離（ $$$D$）および値の差。

また、ニューロンは正方形グリッド上に「張られている」かのように便宜上描かれていることが多いが、これはニューロンがテンソルとして格納されることを意味するものではないことに注意してください $$$\ sqrt {M} \回\ sqrt {M} \回d$。 グリッドは $$$D$。

すぐに紹介します $$$\ガンマ$そして $$$\ alpha$-学習率の減衰と協力の減衰の指標。 厳密に言えばそれらは義務ではありませんが、それらなしではまともな結果を得るのはほとんど不可能です。

アルゴリズム1（標準SOM学習アルゴリズム）：
ログイン： $$$X$、 $$$\ eta$、 $$$\シグマ$、 $$$\ガンマ$、 $$$\ alpha$、 $$$E$

1. 初期化するには $$$W$
2. $$$E$回：
   
   
   1. インデックスリストをランダムに並べ替えます：= shuffle（ $$$[0、1、\ドット、N-2、N-1]$）
   2. それぞれについて $$$idx$注文から：
      
      1. $$$\ vec {x}：= X [idx]$// Xからランダムなベクトルを取得します
      2. $$$i：= \ arg \ min_j {\ left \ | \ vec {x}-\ vec {w_j} \ right \ |}$//最も近いニューロンの番号を見つけます
      3. $$$\ forall j：h_ {ij}：= e ^ {D_ {ij} / \ sigma ^ 2}$//グリッド内のニューロンの近接係数を見つけます。 に注意してください $$$h_ {ii}$常に1
      4. $$$\ forall j：\ vec {w_j}：= \ vec {w_j} + \ eta h_ {ij}（\ vec {x}-\ vec {w_j}）$
   3. $$$\ eta$：= $$$\ガンマ$$$$\ eta$
   4. $$$\シグマ$：= $$$\ alpha$$$$\シグマ$

学習の各エポックでは、入力データセットの要素を調べます。 各要素について、それに最も近いものを見つけます。 $$$x$ニューロン、次にその重みと、レイヤー内のすべての近傍の重みを、距離に応じて更新します $$$x$協力係数について $$$\シグマ$。 以上 $$$\シグマ$、より多くのニューロンが各ステップで効果的に重みを更新します。 次の図は、次の場合のステップA1.2.2.1〜A1.2.2.4のグラフィカルな解釈です。 $$$\シグマ$同じ学習速度と最も近いベクトルでの大きい（1）および小さいとき（2）。


最初の場合 $$$h_ {ij}$団結に近く、そして $$$\ vec {x}$最も近いベクトルが移動するだけでなく、その最初の隣接、さらにはわずかに小さい2番目の隣接も移動します。 2番目のケースでは、同じ隣人がかなり移動します。 どちらの場合も、同じ4番目のベクトル $$$\左\ | \ vec {w_i}-\ vec {w_j} \右\ |$最も近いベクトルから、ただしはるかに大きい $$$D_ {ij}$動かない。

わかりやすくするためにコホーネンマップを学習するいくつかの時代：


アルゴリズムについて簡単に思い出せなかった場合は、 この記事を読んでください。A1の手順について詳しく説明しています。

したがって、SOMの主なアイデア：

• ニューロン間の特定の順序の強制挿入。 $$$D$に優しく転送 $$$W$データスペースに。
• 勝者はすべての戦略（WTA）を取ります。 トレーニングの各ステップで、最も近い「勝つ」ニューロンを決定し、この知識に基づいて重みを更新します。
• 協力は利己主義に発展する $$$\右矢印$グローバルな近似チューニングは、厳密なローカルチューニングに成長します。 さようなら $$$\シグマ$大きくて目立つ部分が更新されます $$$W$WTA戦略は次の場合にはあまり見えません $$$\シグマ$ゼロになる傾向がある $$$w$一度に1つずつ更新されます。

いくつかの些細な変更がすぐに示唆されます：

• 計算にガウスを使用する必要はありません $$$h_ {ij}$ステップA1.2.2.3で。 代替案の最初の候補はコーシー分布です。 ご存知のように、尾がより重いため、協調の段階でより多くのニューロンが変化します。
• 減衰 $$$\ eta$そして $$$\シグマ$指数関数である必要はありません。 シグモイドまたはガウス分岐の形の減衰曲線は、アルゴリズムに大まかなチューニングの時間を与えることができます。
• サイクルで回転する必要はありません $$$E$回。 Wの値が複数の時代にわたって変化しない場合、反復を終了できます。
• トレーニングは通常のSGDに似ています。 このプロセスが最適化するエネルギー関数がないため、「思い出してください」[2]。 厳密な数学はステップA1.2.2.1を台無しにします-最も近いベクトルを取得します。 SOMには修正がありますが、まだエネルギーが残っていますが、詳細を説明します。 重要なのは、これにより、ステップA1.2.2.4で、Nesterovの運動量などの通常の重みの更新の代わりに使用することを妨げないということです。
• 勾配への小さなランダム摂動の追加は、従来の多層ニューラルネットワークの場合ほど有用ではありませんが、still点を回避するための有用な手法であると思われます[3]。
• 自己組織化マップは、バッチトレーニングをサポートします[1]。 彼らのアプリケーションは、トレーニングが悪い構成をより速くスムーズにスキップすることを可能にします $$$W$
• 一部の機能が他の機能よりも重要であることがわかっている場合は、入力値の正規化と入力変数の重みのベクトルの使用を忘れないでください。

ニューロントポロジー

自己組織化カードのやや目立たない変更で、その強さと一意性は構成されていますが、常に忘れているのは初期化フェーズにあります $$$W$そして $$$D$。 例のKohonenレイヤーは常にグリッドとして描かれていますが、これは決して必要ではありません。 それどころか、ニューロンの相互配置を微調整することを強くお勧めします（ $$$D$）データ層。

少なくとも、通常のグリッドの代わりに、六角形のグリッドを使用することをお勧めします。正方形のグリッドは、直線を優先して結果を歪め、六角形のグリッドよりも見た目が悪くなります。 データが周期的であると想定される場合、初期化する価値があります $$$D$ニューロンがテープ上またはトーラス上にあるかのように（下図の番号1を参照）。 明らかにハイパーフォールディングに適合しない3D SOM 3次元データに適合させようとする場合、「フリースカーペット」構造を使用する必要があります（2）。 一部のクラスターが他のクラスターから遠く離れていることがわかっている場合は、「花弁」層構造を試してください（3）。 データに何らかの階層があることがわかっている場合は非常に便利です。 $$$D$この階層のグラフの距離行列を取得できます（4）。

一般的に $$$D$あなたの想像力、データの知識、それに続くニューロンの視覚化の利便性に限定されます。 後者の要因のため、たとえばコホネンの立方体層を行う価値はありません。 ニューロン間の適切な順序を確立することは強力なツールですが、構造が複雑になるほど $$$D$、初期重みを初期化することがより困難です $$$W$そして、出力のKohonen層にいわゆるキンクを取得する可能性が高くなります。 ねじれは、次の場合の学習障害です $$$W$世界的に一貫した $$$D$レイヤーがねじれたり、不自然に引き伸ばされたり、2つのクラスター間で分割されたりする特別なポイントを除き、データ。 同時に、SOM学習アルゴリズムは、既に確立された構造を破壊せずにこの状態から抜け出すことはできません。 ねじれは、通常のニューラルネットワークのトレーニングにおける深い局所的最小値の類似物であることが容易にわかります。

古典的なねじれの抽象的な例：

長い曲線をクラスターに適合させようとするときの合成データのねじれの例。 左上と右の花びらは信じられそうに見えますが、割り当てられたスペースは順序を台無しにします。

レイヤーの重みをランダムに初期化することにより、出力結果が悪いことを実際に保証します。 構築する必要がある $$$W$特定の各領域でニューロンの密度がデータ密度にほぼ一致するようにします。 残念ながら、超感覚能力やデータセットに関する追加情報がなければ、これを行うのは非常に困難です。

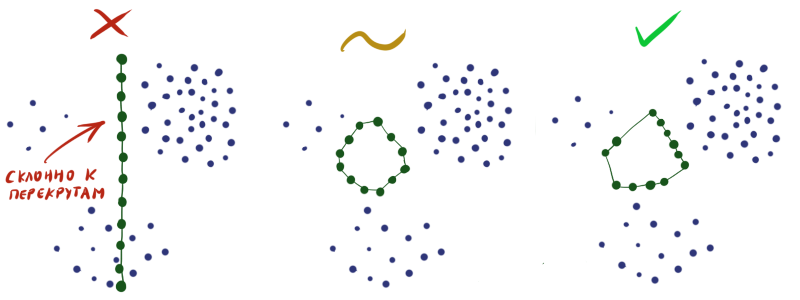
したがって、多くの場合、ニューロンが交差せずにデータ空間全体に単純に均一に分散することを確認する必要があります（中央の図のように）。

勝者の緩和/勝者の強化

このアイデアは、もともとコホネンによって提案され[1]、その後彼の信者によって一般化されました[4]。 勝者ニューロンの更新を削除したり、隣接ニューロンの更新を追加したりするとどうなりますか？ 数学的には、次のようになります。勝者ニューロンのステップA1.2.2.4は、

$$

$$\ vec {w_i}：= \ vec {w_i} + \ eta（（\ vec {x}-\ vec {w_i}）+ \ lambda \ sum_ {j \ neq i} {h_ {ij}（\ vec { x}-\ vec {w_j}）}）$$

どこで $$$\ラムダ$-緩和パラメーター。 残りのニューロンの更新は変更されないままであるか、リラックス期間の一部が追加されます。 それは奇妙に聞こえます。 それが判明した場合 $$$\ラムダ<0$ニューロンには多くの隣人がいるので、そこからロールバックすることさえできます $$$\ vec {x}$？ ベクトルの長さに上からの制限を適用しない場合、次のようになります。

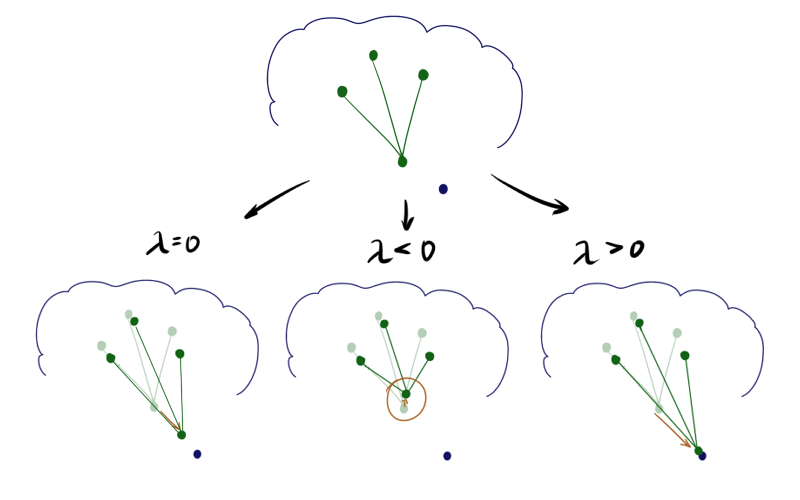
負の $$$\ラムダ$ニューロンは、いわば隣人を自分自身に引き寄せますが、ニューロンが正であれば、反対に、環境から飛び出そうとします。 違いは、トレーニングの開始時に特に顕著です。 同じ初期構成と負、ゼロ、正の最初の時代の後のSOMの状態の例を次に示します $$$\ラムダ$したがって：



上記の影響のため $$$\ラムダ<0$ニューロンはより広いファンから飛び、 $$$\ lambda> 0$-引き出されます。 したがって、最初の場合はコーティングがより均一になり、2番目の場合は小さな孤立したクラスターと放出がより大きな効果を発揮します。 後者の場合、ねじれの可能性もチャートの上部に表示されます。 文献は助言する $$$\ lambda \ in [-1; 1]$、しかし、より大きなモジュロ値でも良い結果が得られることがわかりました。 追加された用語には、 $$$h_ {ij}$順番に依存します $$$\シグマ$。 したがって、上記の手法は、トレーニングの開始時-協力の段階で大きな役割を果たします。

クラスターの洗練段階

アルゴリズムのメインサイクルの後、SOMニューロンが何かに接続されていても、クラスター上のそれらの密度がクラスターがない場所の密度に非常に匹敵することが判明することがよくあります。 そのような状況で分析することはかなり困難です。 Narni Manukyanとチーム[5]は、かなり単純なソリューションを提供します。メインアルゴリズムの後、別のニューロンフィッティングサイクルを開始します。

アルゴリズム2、クラスター調整フェーズ（クラスター調整フェーズ）：
ログイン： $$$X$、 $$$\ eta_ {CR}$、 $$$\ sigma_ {CR}$、 $$$\ gamma_ {CR}$、 $$$\ alpha_ {CR}$、 $$$E_ {CR}$

1. $$$E_ {CR}$回：
   
   
   1. インデックスリストをランダムに並べ替えます：= shuffle（ $$$[0、1、\ドット、N-2、N-1]$）
   2. それぞれについて $$$idx$注文から：
      
      
      1. $$$\ vec {x}：= X [idx]$// Xからランダムなベクトルを取得します
      2. $$$\ forall j：h_ {ij}：= e ^ {\ left \ | \ vec {x}-\ vec {w_j} \ right \ | / \ sigma_ {CR} ^ 2}$//選択したデータ要素に対するニューロンの近接係数を見つけます
      3. $$$\ forall j：\ vec {w_j}：= \ vec {w_j} + \ eta_ {CR} h_ {ij}（\ vec {x}-\ vec {w_j}）$
   3. $$$\ eta_ {CR}$：= $$$\ gamma_ {CR}$$$$\ eta_ {CR}$
   4. $$$\ sigma_ {CR}$：= $$$\ alpha_ {CR}$$$$\ sigma_ {CR}$

アルゴリズムは見た目もA1と非常に似ていますが、現在は最も近いニューロンを探しているのではなく、すべてのニューロンを $$$x$。 相互作用のため $$$\ vec {x}-\ vec {w_j}$A2.2.2.2で指数的に、重みを更新する段階で、実際には、特定のリングにあるニューロンのみが $$$\ vec {x}$。 明確にするために、調整の5つの時代を見てみましょう。

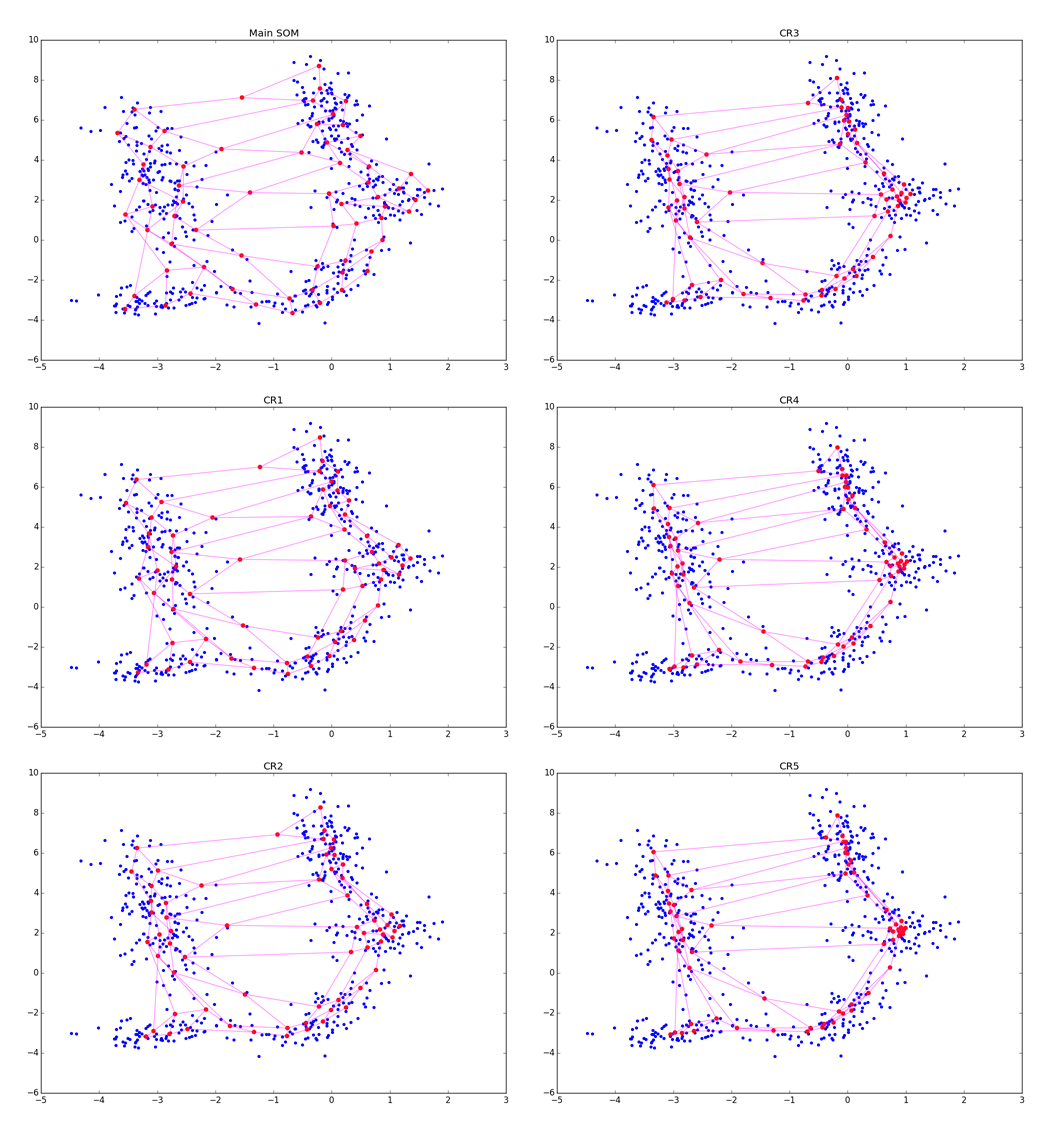
より正確に：CRフェーズでの調整が強いほど、クラスターはよく見えますが、クラスターの形状に関するより多くのローカル情報が失われます。 いくつかの時代の後、血餅の伸びに関するデータのみが残っています。 CRは近くにあるいくつかの折り目を折りたたむことができ、大きすぎる場合 $$$\ sigma_ {CR}$、次の図のように、メインステップで取得した構造を台無しにするだけです。

ただし、指数の代わりに何らかの関数を使用することにより、最後の問題を回避できます。指数は、特定の最大値の後に0になります。

記事の著者は同じを使用することを助言します $$$\ sigma_ {CR}$しかし、これは率直に機能しません：if $$$\ sigma_ {CR}$大きい場合（1のオーダー）、アルゴリズムは行商です。小さい場合（0.01）、何も更新されません。 奇妙なことに、彼らはいくつかの良いデータや変数の重要性の適合ベクトルを持っているのでしょうか？

可視化、SOMの修正

これまでのところ、SOMを使用したデータクラスタリングについて一言も述べていません。 で構築 $$$D$そして $$$W$グリッドは楽しい視覚化ですが、それ自体ではクラスターの数については何も言いません。 さらに、リクエストに応じてグーグルにすることができる美しいマルチカラーのグリッド「SOM視覚化」は、本当に便利なものよりもプレスリリースや人気のある記事の可能性が高いとさえ言えます。

フォールド内のデータクランプの数を判断する最も簡単な方法は、いわゆるU-matrixを注意深く検討することです。 これは、Kohonenマップの一種の視覚化であり、ニューロンの値とともに、ニューロン間の距離が表示されます。 したがって、クラスターが接触している場所と境界が通過する場所を簡単に判断できます。

より興味深い方法は、結果の行列の上で実行することです $$$W$他のクラスタリングアルゴリズム。 たとえば、 DBSCANは 、特に上記のSOM CR修正とともに適しています。 2番目のアルゴリズムの距離関数は、レイヤーのグリッドに沿った距離から結合する必要があります（ $$$D$）およびニューロン間の実際の距離（ $$$\左\ | \ vec {w_i}-\ vec {w_j} \右\ |$）フォールドに関するトポロジ情報を失わないようにします。

しかし、より高度なのは、メインアルゴリズムの操作中に関連するクラスター情報を蓄積することです。 Eren GolgeとPinar Daigulu [6]は、メインアルゴリズムの各エポックにニューロンがアクティブ化された回数を記憶することを提案します（つまり、ニューロンが勝者であるか、ニューロンが勝者に近いため、その重みが更新されます）。ニューロンがクラスターを表すか、空のスペースでハングするか。

アルゴリズム3、SOMの修正（A1に変更あり）：
ログイン： $$$X$、 $$$\ eta$、 $$$\シグマ$、 $$$\ガンマ$、 $$$\ alpha$、 $$$E$

1. 初期化するには $$$W$
2. 初期化するには $$$ES = \ vec {0}$//興奮スコア-ニューロン興奮の合計スコア
3. $$$E$回：
   
   
   1. 初期化するには $$$WC = \ vec {0}$//勝利数-現在の時代のニューロンの興奮の説明
   2. インデックスリストをランダムに並べ替えます：= shuffle（ $$$[0、1、\ドット、N-2、N-1]$）
   3. それぞれについて $$$idx$注文から：
      
      1. $$$\ vec {x}：= X [idx]$// Xからランダムなベクトルを取得します
      2. $$$i：= \ arg \ min_j {\ left \ | \ vec {x}-\ vec {w_j} \ right \ |}$//最も近いニューロンの番号を見つけます
      3. $$$\ forall j：h_ {ij}：= e ^ {D_ {ij} / \ sigma ^ 2}$//グリッド内のニューロンの近接係数を見つけます。 に注意してください $$$h_ {ii}$常に1
      4. $$$\ forall j：\ vec {w_j}：= \ vec {w_j} + \ eta h_ {ij}（\ vec {x}-\ vec {w_j}）$
      5. $$$\ forall j：WC_ {j}：= WC_ {j} + h_ {ij}$//現在のアクティベーションアカウントを更新します
   4. $$$\ eta$：= $$$\ガンマ\イータ$
   5. $$$\シグマ$：= $$$\ alpha \ sigma$
   6. $$$\ forall j：ES：= ES + WC / \ eta$//合計スコアを累積します

ニューロンが勝者である頻度が高いほど、それはクラスターの厚さのどこかであり、その外側ではありません。 総ニューロン数は乗数で累積することに注意してください $$$1 / \イータ$：学習速度が遅いほど、WCの重みが大きくなります。 これは、サイクルの最後のエポックが最初のエポックよりも大きく貢献するように行われます。 これは他の方法でも実行できるため、この特定のフォームに軽くアタッチしてください。

ESは無次元の量であり、その絶対値にはあまり意味がありません。 単純に、値が大きいほど、ニューロンが意味のある何かに結び付けられる可能性が高くなります。 A3の終了後、結果のベクトルを何らかの方法で正規化する必要があります。 ESをニューロンに適用すると、次のようになります。

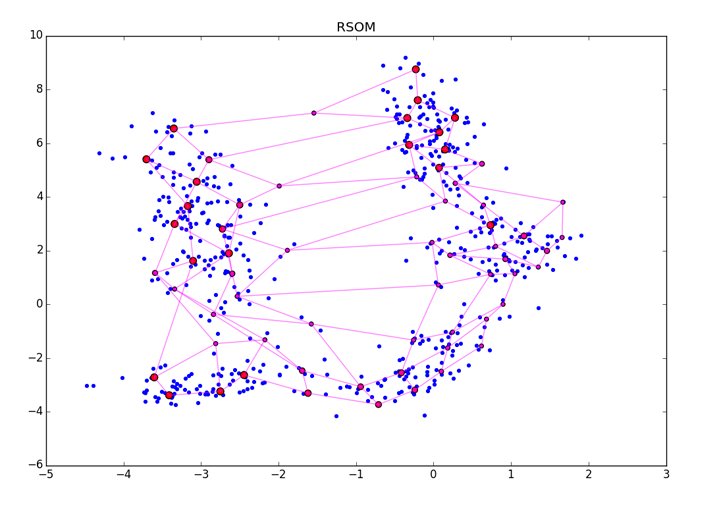
大きな赤い点は励起数が多いニューロン、小さな赤紫は小さいニューロンを表します。 RSOMは、ESの最終処理方法およびデータ内の異なる密度のクラスターに敏感であることに注意してください（図の右下隅を参照）。 ESが正確な値を正確に蓄積できるように、アルゴリズムの収束に必要以上の時代を指定するようにしてください。

もちろん、RSOMと追加のクラスター化ツールの両方を最上部に適用し、視覚化を目で見ることをお勧めします。

その他

レビューに含まれていません。

• カテゴリデータ[7]、シーケンス、画像、およびその他の非ネイティブSOMデータ型[1]を操作するためのSOMの変更。
• グリッドに沿ったニューロンの近接機能の時間的非対称性に関連する作品。
  著者は、これによりねじれと戦うことができると主張している[8]。
• ニューロンによるデータカバレッジの度合いの制御に関する研究（データセットの端での歪みとの戦い）[9]。
• 特定の入力の重要性に関する情報の蓄積[10]。
• SOM [1]を使用したデータのエンコード。
• 初期化の難しい方法 $$$W$[11] [12]。
• 追加の弾性項を追加する機能。 弾力性は、従来のニューラルネットワークにおける正則化の類似物として機能し、混乱を招く構成を禁止します。
• 外れ値の検出。 かなり単純なアイデア：ある時代の後、マップが多かれ少なかれ収束したら、地図からの距離が $$$x$最も近いニューロンへ。 いくつかの時代において、距離が指定されたパラメーターよりも大きく、変化しない場合、サンプルデータを外れ値としてマークできます（オプションとして、更新ステージから除外することもできます）。 マイナス：データセットの「外部」でのみ放出を検出し、その厚さでは検出しません。
• 他の多くの興味深いが、あまりにも特別なもの。

SOMとt-SNEの比較

	ソム	t-SNE
難易度	$$$O（dENM）$	kNN最適化を使用したBarnes-Hut t-SNE- $$$O（dEN \ log {N}）$、しかし、他の実装は、より計算的に集中する可能性があります。 $$$O（dEN ^ 2）$
ハイパーパラメーターの数	3〜5、おそらくニューロンのはるかに+距離行列。 必須の時代数、学習率、協力の初期係数。 学習率の減衰と協調係数もしばしば示されますが、問題はほとんど発生しません。	3〜4、データに関するもっと多くのメトリック。 必要な時代の数、学習率、困惑は、しばしば初期の誇張に遭遇しました。 困惑は非常に魔法であり、間違いなくそれをいじる必要があります。
結果の可視化解像度	ニューロン以外の要素はありません（ $$$M$）	データセットの要素よりも多くの要素はありません（ $$$N$）
可視化トポロジ	いずれにしても、ニューロン間の距離の行列を提供するだけです	通常の平面または3次元空間のみ
さらなる教育、構造の拡大	はい、実装するのは非常に簡単です	いや
追加の変換レイヤーのサポート	はい、Kohonenレイヤーの前に好きなだけ密に接続されたレイヤーまたは畳み込みレイヤーを配置し、通常のバックプロップでトレーニングすることができます	いいえ、手動のデータ変換と機能エンジニアリングのみ
優先クラスタータイプ	デフォルトでは、2次元の折り畳みとエキゾチックなクラスターの形でクラスターを表示します。 次元が2より大きい井戸構造を視覚化するには、トリックが必要です。	ハイパーボールを著しく表示します。 ハイパーフォールディングとエキゾチックはわずかに悪く、距離関数に大きく依存しています。
優先データスペースディメンション	それはデータに依存しますが、もっと悪いです。 アルゴリズムは、 $$$d \ geq 4$、ニューロンによって形成されるハイパーフォールドの自由度が多すぎるため。	任意、次元の呪いが影響し始めるまで
初期データの問題	ニューロンの重みを初期化する必要があります。 ( «»)	いや
	,	,
	SOM
	いや
視覚化におけるクラスター間隔	セマンティックロードを運ぶ	しばしば何も意味しない
視覚化におけるクラスター密度	通常、セマンティックロードがありますが、初期化が不十分な場合は誤解を招く可能性があります	しばしば何も意味しない
視覚化におけるクラスター形状	セマンティックロードを運ぶ	カンニングするかもしれない
クラスタリングの品質を評価することの難しさ	非常に難しい:(	非常に難しい:(

SOMは計算の複雑さで勝つように見えますが、見ずに前もって喜ばないでください。 $$O-bigの下の N 2。$N^2$$$は、自己組織化マップの望ましい解像度に依存します。これは、データの広がりと不均一性に依存し、その結果、暗黙的に依存します$M$$$$N$ そして $$$d$。 現実には、複雑さは次のようなものです $$$O(dN^{\frac{3}{2}}E)$。

この表は、SOMとt-SNEの長所と短所を示しています。自己組織化マップが他のクラスタリング手法に取って代わった理由を理解するのは簡単です：Kohonenマップを使用した視覚化の方が意味がありますが、新しいニューロンを構築し、ニューロンに目的のトポロジを設定できます。$$は、現代のデータサイエンスにおけるSOMの関連性を大きく損ないます。さらに、t-SNE視覚化をすぐに使用できる場合、自己組織化カードには後処理および/または追加の視覚化の努力が必要です。追加のマイナス要因-初期化の問題$d$$$およびねじれ。これは、自己組織化マップが過去のデータサイエンスにあるということですか？$W$

そうでもない。いいえ、いや、時にはあまり多次元でないデータを処理する必要があります-このため、SOMを使用することはかなり可能です。視覚化は本当にきれいで壮観です。アルゴリズムに洗練を適用するのが面倒ではない場合、SOMはハイパーフォールド上のクラスターを完全に検出します。

ご清聴ありがとうございました。私の記事が、誰かが新しいSOMビジュアライゼーションを作成するきっかけになることを願っています。githubから、記事で提案されている主な最適化を含む最小限のSOMの例を含むコードをダウンロードし、アニメーション化されたマップトレーニングを見ることができます。次回は、競争トレーニングにも基づいた「神経ガス」アルゴリズムを検討します。

[1]：自己組織化マップ、本。 Teuvo Kohonen
[2]：自己組織化マップのエネルギー関数。トム・ヘスケサ、理論財団SNN、ナイメーヘン大学
[3]：bair.berkeley.edu/blog/2017/08/31/saddle-efficiency
[4]：勝者リラックス型自己組織化マップ、Jens Christian Claussen
[5]：まばらに一致した自己組織化マップでのデータ駆動型クラスター強化と可視化。 Narine Manukyan、Margaret J. Eppstein、およびDonna M. Rizzo
[6]：Web画像からの自動概念学習のための自己組織化マップの修正。 Eren Golge＆Pinar Duygulu
[7]：バイナリおよびカテゴリー自己組織化マップの代替アプローチ。 Alessandra Santana、Alessandra Morais、Marcos G. Quiles
[8]：複数勝者の自己組織化マップでのシーケンス処理をサポートする一時的非対称学習
[9]：自己組織化マップおよび神経ガスでの拡大制御。 Thomas Villmann、Jens Christian Claussen
[10]：自己組織化マップにおけるニューロン選択のための埋め込み情報強化。上村亮太郎、上村多恵子
[11]：自己組織化マップの初期化問題。Iren Valova、George Georgiev、Natacha Gueorguieva、Jacob Olsona
[12]：自己組織化マップの初期化。Mohammed Attik、Laurent Bougrain、Frederic Alexandre