大小のグラフ：プレゼンテーション選択の問題に対するインテリジェントなソリューション

（プログラマ向けのエチュードまたは新しいタイプのインターネット検索のリクエスト）



フライから象を作成するプログラム （以下、MSプログラムと呼びます）は、指定された文字数の名詞の無向グラフには数千の頂点が含まれていますが、 完全なグラフに対してかなり「細い」（つまり、エッジが比較的少ない）ことを示しました彼は遠く離れています（例1を参照）。 著書 『 Etudes for Programmers 』の著者であるCharles Wetherellに続き、彼はそのようなグラフを表現 するさまざまな方法を提示するためにエチュードのジャンルを選択しました。 （そして、これから結論を引き出して、プレゼンテーションの選択を自動化します-おそらく新しいタイプのインターネット検索に至るまで）。

Start for word length 8
6016 words loaded from dictionary file: ..\Dictionary\ORF3.txt
Graph was made: edges number = 871

例1. 8文字の名詞グラフの特性。

控えめに言っても、「パフォーマンスの提示」は荒いように聞こえますが、私の意見では、そのような粗さはエチュードのジャンルと最も一致しており、いくつかの異なるバリエーションの概要を示しています（Weserellによる）。 考えられるすべてのケースに対して設計を行いますが、最終的な完全なソリューションは提供しません。 実装の二次的な純粋に技術的な詳細にこだわるつもりはありません。そして、それらを使って調査を過負荷にしないために、本質のために最も重要なコードの断片のみを引用します。 前述のMSプログラムのように（コードの再利用の理由を含む）、古いOO Pascal Delphi-7を使用します。このようなシンプルで広く知られている言語が読みやすく、必要に応じて、より現代的なユニバーサル言語に簡単に翻訳できることを願っていますプログラミング。 グラフ理論の基礎については触れません-それらは、以下で使用される他のものと同様に、ウィキペディアで概念と用語を明確にすることができます-場合によってはリンクを提供します。 しかし同時に、私はwiki記事の正確性に対する責任を完全に拒否します。各記事には、Wikiルールに従って、信頼できるソースへのリンクがあり、これらのソースは最終的な説明に使用されるべきです。

また、説明する「スキニー」グラフは、単語ゲームだけでなく、より深刻なタスクにも必要であることに注意してください。 たとえば、 コンピューター（数学）有機化学では、化学分子は、頂点が原子に対応し、化学結合がエッジに対応するグラフとして表されます。 このような表現（正式な論理的アプローチと呼ばれることもあります）は、伝統的に構造式とボールロッドモデルを使用する有機化学の古典的な構造理論に対応しています 。 そして、現代のすべての化学者は、原子がボールのようなものではなく、原子間の結合がロッドのようなものではないことを確実に知っていますが、これらのモデルは化学において広く成功裏に適用され続けています。 有機分子の骨格は主に四価炭素で構成されているため、それらを表すグラフの頂点の次数は4を超えません。 確かに、例外は可能です。たとえば、 フェロセン分子のグラフでは、鉄原子に対応する頂点の次数は10です。完全なグラフはシクロプロパンの炭素骨格のみで、残りは非常に不完全です。 このスケッチは、グラフを使用した一定の大量作業には役立ちそうにありませんが、ゲームなどの状況問題を解決するのに役立つことを願っています。 いずれにしても、この簡単な例により、プレゼンテーションの選択（AIの使用を含む）の問題に対する知的解決策のアイデアを説明できます。

MSプログラムの場合と同様に、各表現では、グラフの頂点の特定のペア間の最短パスを検索します。 TGraphクラスを定義することから始めましょう。

  TGraph = class(TObject) protected procedure initA (vNum, eNum : integer); virtual; abstract; procedure addEdgeA (v,u : integer); virtual; abstract; function isEdgeA (v,u : integer) : Boolean; virtual; abstract; private vertNum : integer; //   edgeNum : integer; //   adjMatrix : array of array of Boolean; //   degVector : array of integer; //    predV : array of integer; //        path : array of integer; //  pathLen : integer; //   (    1) public testPairV1, testPairV2 : integer; //   constructor create; destructor free; function getVertNum : integer; //    function getEdgeNum : integer; //    function deg (v : integer) : integer; //    procedure init (vNum, eNum : integer); //   procedure addEdge (v,u : integer); //   (v,u) function isVertex (v : integer) : Boolean; // true,  0<=v< vertNum function isEdge (v,u : integer) : Boolean; // true,    (v,u)   procedure make (eNum,maxDeg : integer); //    procedure copy (g : TGraph); //     g function BFSsp(v,u : integer) : Boolean; //     BFS procedure getShortestPath (v,u : integer); //     path function pathToStr {(v : integer)} : string; //   path    string function getShortestPathStr (v,u :integer) : string; //    function findTestPair : string; //     end; 

子孫からの置換には、保護された（保護された）抽象メソッドが必要です。 例：

  procedure TGraph.addEdge (v,u : integer); begin addEdgeA (v,u); end; 

使用される動的配列では、インデックス付けはゼロから始まりますが、グラフ理論に関する多くの本では、頂点とエッジの番号付けは1から始まります。 グラフを接続する必要がないため、入力するとき（これについては後で説明します）、デフォルトで孤立したゼロの頂点を許可し、本の最初の頂点からグラフを入力できます。

隣接行列（adjMatrix）を使用したグラフ表現は、おそらく最も一般的で普遍的な表現の1つです。 一般的な場合、この行列は、エッジ（v、u）が要素adjMatrix [v、u] = true（初期化中にfalseがすべての要素に書き込まれる）に対応する有向グラフとして表すことができます。 このようなグラフは次のように定義できます。

  TDirectedGraph = class(TGraph) protected procedure initA (vNum,eNum : integer); override; procedure addEdgeA (v,u : integer); override; function isEdgeA (v,u : integer) : Boolean; override; end; 

同じクラスを無向グラフに使用できます。 この場合、頂点のペア（v、u）に入射する無向グラフのエッジは、有向グラフのエッジ（v、u）および（u、v）に対応します。 これが私たちがやることです。 したがって、エッジの追加メソッド（addEdgeA）は次のように定義されます。

  procedure TDirectedGraph.addEdgeA (v,u : integer); var i,j : integer; begin if not adjMatrix [v,u] then begin adjMatrix [v,u] := true; adjMatrix [u,v] := true; inc (edgeNum); //   1   inc(degVector [v]); //   1   v inc(degVector [u]); //   1   u end; end; 

エッジが比較的少ない場合、隣接行列は疎になります。 このような行列の使用については、 S。Pissanetski、Sparse Matrix Technology、M .: Mir、1988の本で詳しく説明されています。 ここでは、ここで説明されているかなり洗練された手法を適用しようとはせず、下三角サブマトリックスのみを使用してこのマトリックスを単純に「半分」にします。 ループのあるグラフは考慮しないため、メインの対角線は必要ありません。 別のクラスを定義します。

  TUndirectedGraph = class(TGraph) protected procedure initA (vNum,eNum : integer); override; procedure addEdgeA (v,u : integer); override; function isEdgeA (v,u : integer) : Boolean; override; public procedure clear; end; 

次の初期化メソッドを使用できます。

  procedure TUndirectedGraph.initA (vNum, eNum : integer); var i,j : integer; begin degVector := nil; predV := nil; path := nil; vertNum := vNum; setLength (adjMatrix,vertNum-1); setLength (degVector,vertNum); for i:=0 to vertNum-2 do begin degVector [i] := 0; setLength (adjMatrix [i], i+1); for j := 0 to i do adjMatrix [i,j] := false; end; degVector [vertNum-1] := 0; end; 

この場合、エッジの追加メソッド（addEdgeA）は、有向グラフの場合とは異なります。

 procedure TUndirectedGraph.addEdgeA (v,u : integer); var i,j : integer; begin if v>u then begin i := v-1; // i := max (v,u)-1; j := u; // j := min (v,u); end else if v<u then begin i := u-1; j := v; end else exit; if not adjMatrix [i,j] then begin adjMatrix [i,j] := true; inc (edgeNum); inc(degVector [i]); inc(degVector [j]); end; end; 

同様に、isEdgeAメソッドの実装方法は異なります。

 function TDirectedGraph.isEdgeA (v,u : integer) : Boolean; begin Result := adjMatrix [v,u]; end; function TUndirectedGraph.isEdgeA (v,u : integer) : Boolean; begin if u<v then Result := adjMatrix [v-1,u] else if u>v then Result := adjMatrix [u-1,v] else Result := false; end; 

では、非常に大きなグラフ、たとえば100万個の頂点を処理する方法について考えてみましょう。 -このようなサイズの三角形の隣接行列でさえ、大きすぎる場合があります！ 以下の定義を作成します。

 TEdgeRec = record v1,v2 : integer; end; TBigUndirectedGraph = class(TGraph) protected procedure initA (vNum,eNum : integer); override; procedure addEdgeA (v,u : integer); override; function isEdgeA (v,u : integer) : Boolean; override; private edgeIndex : integer; edges : array of TEdgeRec; nbVertex : array of integer; //  nbStart : array of integer; //        nbCount : array of integer; //    public destructor free; procedure calcNb; //   end; 

エッジが比較的少ないスキニーグラフで作業していることを考えると、エッジエッジベクトルのエッジに付随する頂点のペアを覚えています。

 procedure TBigUndirectedGraph.addEdgeA (v,u : integer); begin with edges [edgeIndex] do begin v1 := v; v2 := u; end; inc (edgeIndex); inc(degVector [v]); inc(degVector [u]); end; 

このアプローチは、隣接リストの形式でのグラフの最も経済的な表現の1つに対応します。 特に、グラフを手動で入力するのに非常に便利です。 次の形式を使用して、エッジを記録できます。

vu

ここで、v、uはエッジに付随する頂点です。

エントリは文字列で作成され、カンマで区切られます。 単純な場合でも、行を入力する方が便利です。

1-2,2-3,3-1

3x3隣接行列を入力するよりも。

ただし、よくあることですが、プログラムがエッジベクトルエッジを直接操作する場合、メモリ量を節約することは時間の浪費になる可能性があります。 実際、isEdgeAメソッドでは、すべてのエッジを反復処理する必要がある場合があります。 もちろん、このベクトルを並べ替えて半分に分割して検索することもできますが、各頂点の角度を小さくすると、より高速な方法を使用できます。 ベクトルnbVertexには、各頂点の近傍を書き込みます。 頂点の近傍の数はその次数に対応するため、頂点がゼロの近傍は次のように記述されます。

NbVertex [0], …, nbVertex[deg(0)-1]

次に、最初の頂点の近傍なども同様に記述されます 各頂点の最初の各近傍のインデックスは、nbStartベクトルに保存されます。

nbStart[0]=0, nbStart[1]= deg(0),…

このようなインデックスは、補助ベクトルnbCountを使用するメソッドによって実行されます。

 procedure TBigUndirectedGraph.calcNb; var i,n : integer; begin n := 0; for i:=0 to vertNum-1 do begin nbStart [i] := n; nbCount [i] := n; inc (n, degVector [i]); end; for i:=0 to edgeNum-1 do begin nbVertex [nbCount[edges [i].v1]] := edges [i].v2; inc (nbCount[edges [i].v1]); nbVertex [nbCount[edges [i].v2]] := edges [i].v1; inc (nbCount[edges [i].v2]); end; end; 

頂点のペア（v、u）のisEdgeAメソッドは、最大でdeg（v）nbVertex要素の列挙を必要とします。

 function TBigUndirectedGraph.isEdgeA (v,u : integer) : Boolean; var i,n,d : integer; begin d := deg (v); if d>0 then begin n := nbStart [v]; for i:=0 to d-1 do begin Result := nbVertex[n+i]=u; if Result then exit; end; end else Result := false; end; 

このような検索は、指定された制限内の複数の位置から独立して実行できるため、非常に大きなグラフで大きなパワーを持つ頂点が見つかった場合、検索を簡単に並列化できます。 一部のアルゴリズムでは、エッジの追加と削除が必要になる場合があります。 これは上記の表現では簡単にできますが、後者の場合はそうではなく、明らかにマイナスです。 ただし、目的のために-最短パスを見つける-エッジを追加および削除する必要はありません。

最短経路を見つけましょう。 使用されているBFSアルゴリズムは古典的であり、Wikipediaで再販された多くの本で詳しく説明されているため、その説明を省略して実装を示します。

 function TGraph.BFSsp(v,u : integer) : Boolean; //     BFS var Qu : array of integer; first, last : integer; i,p : integer; newV : array of Boolean; begin p := v; setLength (predV,vertNum); setLength (newV,vertNum); for i:= 0 to vertNum-1 do newV [i] := true; setLength (Qu,vertNum); first := 0; last := 1; Qu [last] := p; newV [p] := false; while (first<last) and (p<>u) do begin inc (first); p := Qu [first]; for i:=0 to vertNum-1 do if isEdge (p,i) and newV [i] then begin inc (last); Qu [last] := i; newV [i] := false; predV [i] := p; end; end; Result := p = u; Qu := nil; newV := nil; end; // BFSsp procedure TGraph.getShortestPath (v,u : integer); var i,p : integer; begin setLength (path,vertNum); p := u; i := 0; path [0] := p; while p<>v do begin inc (i); p := predV [p]; path [i] := p; end; // inc (i); pathLen := i+1; setLength (path,pathLen); end; // getShortestPath 

3つの異なるグラフ表現の記述されたクラスは、プログラムが作成されたデバッグとテスト（およびこの調査のデモンストレーション）のために別のモジュールに実装されました-プログラムTと呼びましょう。このプログラムのウィンドウのスクリーンショットを図に示します。



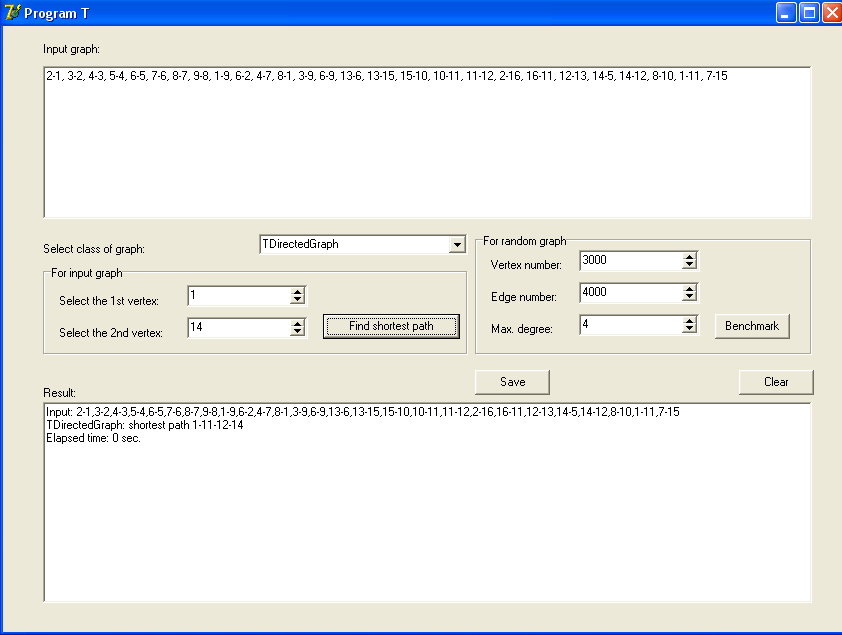
[入力グラフ]フィールドに、グラフの隣接のリストを上記の形式で入力できます。 [結果]フィールドに、プログラムはメッセージと作業結果を表示します。 この出力は、[保存]ボタンを使用してテキストファイルに保存でき、[クリア]ボタンを使用してフィールドをクリアできます。 [グラフのクラスを選択]ドロップダウンリストを使用すると、説明されているビューのいずれかを選択できます。 それらの数は少なく、開発中（設計時）に手動で入力することも可能ですが、将来他のビューが追加される可能性があるため、実行時に（実行時に）リストにデータを追加します。 これを行うには、メインフォームを作成するための次の簡単なイベントハンドラーを作成します。

 procedure TMainForm.FormCreate(Sender: TObject); begin dg := TDirectedGraph.create; ug := TUndirectedGraph.create; bg := TBigUndirectedGraph.create; ComboBoxClass.AddItem(dg.ClassName,dg); ComboBoxClass.AddItem(ug.ClassName,ug); ComboBoxClass.AddItem(bg.ClassName,bg); ComboBoxClass.ItemIndex := 0; end; 

ここで作成されたグラフ（dg、ug、bg）を使用すると、プログラムは引き続き動作します。 隣接リストの解析とブロードキャストは簡単なため、読者の説明に読者の注意を無駄にさせません。 プログラムの2番目のメインテストに進みましょう。ユーザー定義のパラメーターを使用して、ランダムグラフ内の頂点のランダムペア（テスト頂点）間の最短パスを見つけます。 このようなグラフを生成するには、親クラスに次の簡単なメソッドを追加します。 メソッドパラメータ-頂点の数と頂点の最大次数：

 procedure TGraph.make (eNum, maxDeg : integer); var n,i,j : integer; begin randomize; n := 0; repeat i := random (vertNum); // 1-   j := random (vertNum); // 2-   if (i<>j)and (deg(i)<maxDeg) and (deg(j)<maxDeg) then begin addEdge (i,j); inc (n); end; until n= eNum; end; 

生成されたグラフをコピーするには、次の簡単な方法を使用できます。

 procedure TGraph.copy (g : TGraph); //     g var i,j : integer; begin for i:=1 to vertNum-1 do for j := 0 to i-1 do if g.isEdge (i,j) then addEdge (i,j); end; 

テスト頂点の検索も複雑になりませんでした（インターネットでの詳細な非研究の研究では、ランダムグラフを生成するための多くの優れた手順を見つけることができます）。

 function TGraph.findTestPair : string; var i,j,maxV1,maxV2 : integer; maxLen : integer; begin maxLen := 0; maxV1 := 0; maxV2 := 0; for i := 1 to maxGen do begin testPairV1 := random (vertNum); // 1-   j := 0; repeat testPairV2 := random (vertNum); // 2-   inc (j); until ((testPairV1<>testPairV2) and (not isEdge (testPairV1, testPairV2))) or (j=maxGen); if BFSsp(testPairV1, testPairV2) then begin getShortestPath (testPairV1, testPairV2); if pathLen > maxLen then begin maxLen := pathLen; maxV1 := testPairV1; maxV2 := testPairV2; end; path := nil; end end; testPairV1 := maxV1; testPairV1 := maxV2; Result := 'Test vertex pair '+intToStr(testPairV1)+', '+ intToStr(testPairV2)+' Path length '+ intToStr(maxLen); end; 

10に等しいmaxGen定数を使用しましたが、運が良ければ、すべての世代が適切であるとは限りません。 典型的な結果の1つを示します。

--- Benchmark ---------
Vertex number: 3000 Edge number: 4000 Max degree: 4
TDirectedGraph: Test vertex pair 2671, 853 Path length 12
TDirectedGraph: shortest path 2671-2629-2646-1658-499-2625-354-1027-626-733-2641-853
Elapsed time: 0.0160002149641514 sec.
TUndirectedGraph: shortest path 2671-2629-2646-1658-499-2625-354-1027-626-733-2641-853
Elapsed time: 0.030999630689621 sec.
TBigUndirectedGraph: shortest path 2671-2629-2646-1658-499-2625-354-1027-626-733-2641-853
Elapsed time: 0.0470004742965102 sec.

他の問題では、時間差はさらに小さくなりますが、全体的に傾向があります

$$

$$t_ {TDirectedGraph} \ leqslant t_ {TUndirectedGraph} \ leqslant t_ {TBigUndirectedGraph}、$$

どこで $$$t$-時間。

したがって、一方では、（使用されているものから）プレゼンテーションの変更は特に速度に影響を与えないかもしれませんが、一方では、特定のタスクおよび予想されるタイプのグラフでは、異なるビューを試す価値があります。 彼は「提案」という言葉を特に強調しました。 示されている結果は、カテゴリ別の推奨事項にはあまりにも緩いものです。 別のタスクでは、質的に異なる結果が表示される場合があります。 おそらく、すべての場合に1つの表現を選択することはできません。 これに関連して、次の考えが現れます。 通常、説明されているTプログラムなどのプログラムは、ライブラリの開発と最終テストの段階で使用されますが、ユーザーには届きません。 同時に、多くの大規模なライブラリでは、同じことを行う関数を見つけることができますが、異なる構造と異なるメソッドのデータを使用します。 このような場合、開発者がツールを使用して、ライブラリが意識的かつ十分な情報に基づいた選択を行えるようにすると非常に役立つと思います。 次の段階的なステップは、必要なテストを生成するためのユーザーパラメーターを受け取り、これらのテストの結果に基づいてアルゴリズムとデータ構造を選択し、ライブラリリソースの使用に関するユーザーへの推奨事項を提供するプログラムです。 タスクとサポート機能に応じて、テストを生成できるだけでなく、ローカルデータベース、サポートサイトから、またはインターネットでのグローバル検索の結果としてダウンロードすることもできます。 テストサンプルでは、​​顧客には明らかでない機能を備えたグラフが表示される場合があります。 テストでは、このような機能が自動的に考慮されます。 これは、このスケッチのタイトルに記載されている表現を選択する問題に対する知的（AI、おそらくAI +自然知能）ソリューションになります。

もっともっと。 ここで、必要なライブラリを見つけるために、「グラフ内の最短パスを見つける」などの検索エンジンに入力します。 次に、数十万のリンクから私たちのケースに最適なものを見つけるのに役立つ奇跡を期待しています。 ライブラリに標準化されたネットワークプロトコル（おそらく新しいプロトコルが必要になる）を備えたTプログラムが装備されている場合、ユーザーは一連のテストを検索エンジンに送信し、Tプログラムサーバーがこれらのテストを実行します。 検索エンジンは結果を分析し、このケースに最適なライブラリへの要求リンクに応答して提供します。 同時に、クエリを送信するときに、検索エンジンは以前の同様のクエリの結果を考慮することができます。 これは、新しいタイプの検索になります。 現在、ライブラリはダウンロード数ごとに評価を受け取り、そのような検索の場合、ユーザーのテストタスクを満足させるための評価を受け取ります。 格付けは大幅に差別化されます。1つの要求グループには最大パフォーマンスの優先順位があり、もう1つにはメモリの節約があり、3番目には無料ライブラリへのリンクのみの追加要件がある場合があります。 もちろん、異なるサーバーで得られた結果を比較することは、サーバーの計算能力に補正係数を使用しても、非常に近似します。 事前に選択したオプションの最終比較は、クライアントコンピューターで行う必要があります。

今、インターネット上で、あらゆる種類のオンライン計算機とファイル形式コンバーターの束を見つけることができます-だから、オンラインで何でも数えて変換できるようです。 しかし、これは結果に反対の焦点を当てたサービスであり、その後のオフライン使用の選択ではありません。

結論として、グラフの表現は上記のものよりもはるかに多いことに注意する価値があります。たとえば、リンクを使用したバイナリツリー（非常に「細い」グラフ）の表現は、Wirthの古典的な作品で詳細に説明されています。以下を定義することにより、容量を8倍に増やすことができます。

 adjMatrix : array of array of Byte; 

各エッジは1ビットに対応するため、8つのエッジが1バイトにパックされます。マニュアルでは、最大のパフォーマンスはCardinalタイプ（4バイト）によって提供されるため、そのようなデータ構造が適切である可能性があると述べています。

 adjMatrix : array of array of Cardinal; 

そのようなアプローチの例は、Komosko LF、Batsyn MV、ビット演算を使用したグラフの色付けの問題を解決するための高速アルゴリズム、第38回会議「情報技術とシステム-2014」、N。Novgorod：IPPI RAS、2014、C.432。 bsf（ビットスキャンフォワード）CPU命令を使用したグラフのビット表現により、ほぼ17倍の平均プログラムアクセラレーションを取得できました。多くの多様なグラフ表現がGPUに使用されます（例を参照）。

別の重要なトピックは、セットを使用したグラフの表現です。

 adjMatrix : array [1..maxVertNum] of set of 1.. maxVertNum; 

実際、多数の概念は現代の数学の基本であり、プログラミングで同じように広く使用するのが自然でしょう。グラフを含む。ただし、ここでは困難が発生します。たとえば、Delphiでは、セットの最大出力（maxVertNum）は非常に制限されています。したがって、大きなグラフの場合、大きなセットを表すための特別な手法が必要です。さらに、示された要素に続くセットを選択するための便利で効果的な手順はありません。この欠陥はWirth Pascal以来存在しており、OS 360/370の絶望的に古くなったPascal 8000でのみ拡張が行われたようです-ループ演算子forall：

forall i in aSet do

この演算子はセットの列挙要素の標準的なかさばる構造を置き換えることを許可しました：

 for i:=minI to maxI do if i in aSet then 

セットが非常に小さい場合は、テーブル実装で次の要素を選択できます。セットが大きい場合は、簡単なアセンブリ手順を実行できます。