はじめに
自動制御システム(ACS)の正常性に必要な条件は、その安定性です。 安定性により、システムの特性を理解して、その影響が終了した後、妨害要因の影響下で派生した平衡状態を復元するのが慣例です[1]。
問題の声明
産業用ロボットおよびマニピュレーターの性能の前提条件である自動制御システムの安定性を計算する問題を解決するための、シンプルで明確でアクセス可能なツールを入手します。
理論はシンプルで簡潔です
ミハイロフ法によるシステムの安定性の分析は、閉システムの特性多項式(伝達関数の分母)、複素周波数関数(特性ベクトル)の構築に帰着します。
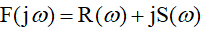
(1)
どこで
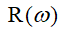
そして
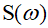
-それぞれ、伝達関数の分母の実数部と虚数部。その形式により、システムの安定性を判断できます。
閉じた自走砲は、複素周波数関数が

で始まる
矢印は原点であり、連続してn象限を通過します。ここで、nはシステムの特性方程式の次数です。
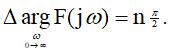
(2)
図1.ミハイロフ基準の振幅位相特性(ホドグラフ):a)-安定したシステム。 b)-不安定なシステム(1、2)および安定境界上のシステム(3)
自走砲電動マニピュレーター産業用ロボット(MPR)
図2-MPR電気駆動を備えた自走砲の構造図
この自走砲の伝達関数は次の式を持ちます[2]:
(3)
ここで、kyは増幅器のゲイン、kmはアーマチュアの電圧に対するエンジン速度の比例係数、Tyは増幅器の電磁時定数、Tmは負荷慣性を考慮したエンジンの電気機械的時定数です(動的特性の観点から、エンジンは慣性の伝達関数であり、積分リンク)、kds-速度センサーの入力値と出力値の間の比例係数、K-ゲイン ニアメイン回路:
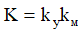
。
伝達関数の式の数値は次のとおりです。
K = 100 deg /(V∙s); kds = 0.01 V /(deg s); Ty = 0.01秒; Tm = 0.1s。
次に、閉じたシステムの特性多項式を書きます

sを
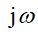
:

(4)
Pythonソリューション
ここで、Pythonでそのような問題を解決した人はいませんでした。 これは、複素数を処理する能力が制限されていたためです。 SymPyの登場により、次のことができるようになりました。
from sympy import * T1,T2,w =symbols('T1 T2 w',real=True) z=factor ((T1*w*I+1)*(T2*w*I+1)*w*I+1) print (" -\n%s"%z)
ここで、Iは虚数単位、wは循環周波数、T1 =T= 0.01、T2 = Tm = 0.1
多項式の展開式を取得します。
閉じたシステムの特性多項式は
-I * T1 * T2 * w ** 3-T1 * w ** 2-T2 * w ** 2 + I * w + 1多項式が3次であることがすぐにわかります。 次に、シンボリックマッピングの虚数部と実数部を取得します。
zr=re(z) zm=im(z) print(" Re= %s"%zr) print(" Im= %s"%zm)
取得するもの:
実部
Re = -T1 * w ** 2-T2 * w ** 2 + 1虚数部
Im = -T1 * T2 * w ** 3 + wすぐに実部の2次と3次の虚数が表示されます。 ミハイロフのホドグラフを作成するためのデータを準備します。 T1とT2の数値を導入し、0.1のステップで周波数を0から100に変更し、グラフを作成します。
from numpy import arange import matplotlib.pyplot as plt x=[zr.subs({T1:0.01,T2:0.1,w:q}) for q in arange(0,100,0.1)] y=[zm.subs({T1:0.01,T2:0.1,w:q}) for q in arange(0,100,0.1)] plt.plot(x, y) plt.grid(True) plt.show()

グラフからは見えませんが、ホドグラフは実際の正の軸から始まります。 軸のスケールを変更する必要があります。 プログラムの完全なリストを提供します。
from sympy import * from numpy import arange import matplotlib.pyplot as plt T1,T2,w =symbols('T1 T2 w',real=True) z=factor((T1*w*I+1)*(T2*w*I+1)*w*I+1) print(" -\n%s"%z) zr=re(z) zm=im(z) print(" Re= %s"%zr) print(" Im= %s"%zm) x=[zr.subs({T1:0.01,T2:0.1,w:q}) for q in arange(0,100,0.1)] y=[zm.subs({T1:0.01,T2:0.1,w:q}) for q in arange(0,100,0.1)] plt.axis([-150.0, 10.0, -15.0, 15.0]) plt.plot(x, y) plt.grid(True) plt.show()
取得するもの:
閉システムの特性多項式
--I * T1 * T2 * w ** 3-T1 * w ** 2-T2 * w ** 2 + I * w + 1実部
Re = -T1 * w ** 2-T2 * w ** 2 + 1虚数部
Im = -T1 * T2 * w ** 3 + w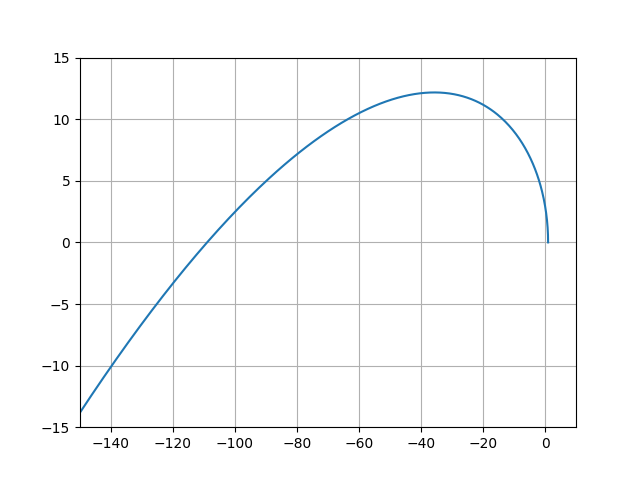
ホドグラフが実際の正の軸から始まることが明らかになりました。 自走砲は安定しており、n = 3であり、ホドグラフは最初の図に示したものと一致します。
さらに、プログラムにw = 0の次のコードを追加することで、ホドグラフが実際の軸で開始することを確認できます。
print(" (%s,%s)"%(zr.subs({T1:0.01,T2:0.1,w:0}),zm.subs({T1:0.01,T2:0.1,w:0})))
取得するもの:
開始点M(1.0)自走砲
溶接ユニット(NSU)の先端は、車体のさまざまな場所に運ばれ、迅速かつ正確に必要なアクションを実行します。 NSUの位置決めにより、自走砲のミハイロフ基準により安定性を判断する必要があります。
図3. NSUを配置する自走砲の構造図
この自走砲の特性方程式は[1]のようになります。
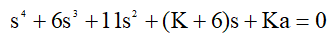
ここで、Kはシステムの可変ゲイン、aは明確な正の定数です。 数値:K = 40; a = 0.525。
次に、sを
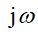
、ミハイロフ関数を取得します。
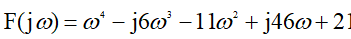
(5)
Pythonソリューション
rom sympy import * from numpy import arange import matplotlib.pyplot as plt w =symbols(' w',real=True) z=w**4-I*6*w**3-11*w**2+I*46*w+21 print(" -\n%s"%z) zr=re(z) zm=im(z) print(" (%s,%s)"%(zr.subs({w:0}),zm.subs({w:0}))) print(" Re= %s"%zr) print(" Im= %s"%zm) x=[zr.subs({w:q}) for q in arange(0,100,0.1)] y=[zm.subs({w:q}) for q in arange(0,100,0.1)] plt.axis([-10.0, 10.0, -50.0, 50.0]) plt.plot(x, y) plt.grid(True) plt.show()
取得するもの:
閉システムの特性多項式は、
w ** 4-6 * I * w ** 3-11 * w ** 2 + 46 * I * w + 21です。開始点
M(21.0)実数部
Re = w ** 4-11 * w ** 2 + 21虚数部
Im = -6 * w ** 3 + 46 * w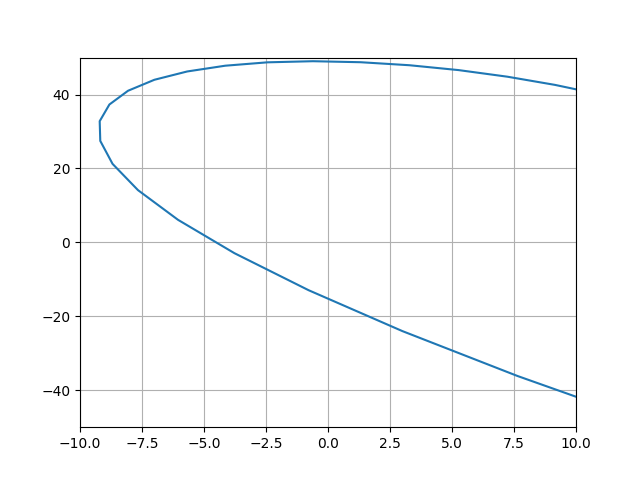
実際の正の軸(M(21.0))から始まるミハイロフの構築されたホドグラフは、原点を正方向に回り、4つの象限を連続して通過します。これは特性方程式の次数に対応します。 そのため、この自走砲はNSIを位置決めします-安定しています。
結論
SymPy Pythonモジュールを使用して、産業用ロボットおよびマニピュレーターの性能の前提条件である自動制御システムの安定性を計算する問題を解決するためのシンプルで直感的なツールが得られました。
参照資料
- Dorf R.現代の制御システム/ R. Dorf、R。Bishop。 -M .: 2002年基礎知識研究所。-832 p。
- ユレビッチE.I. Robotics 2nd Editionの基礎/ E.I. ユレビッチ。 -サンクトペテルブルク:BHV-Petersburg、2005。-416 p。