フラクタル、マルチンゲール、ランダム積分について。 パート1

私の意見では、確率計算は、数式が詩と出会う高等数学の壮大なセクションの1つです（トポロジーと複雑な分析とともに）。 これは、彼らが美を見つける場所、芸術的創造の範囲が始まる場所です。 記事「 ウィーナーカオス」または 「 コインを弾く別の方法」という記事を読んだ人の多くは、たとえ少し理解していても、この理論の素晴らしさを理解できました。 今日は数学の旅を続け、ランダムプロセス、自明でない統合、金融数学、さらには関数型プログラミングの少しの世界に飛び込みます。 私たちは深刻な会話をしているので、警戒します。


ところで、別の記事を読むことに興味があるなら、突然、

$$

$$dX ^ 2 \ neq 2X \ cdot dX、$$

投票を残すことができる投票を以下に追加しました。

フラクタルの隠れた脅威

簡単な機能を想像してください $$$f（t）$ ある間隔で $$$[t、t + \ Delta t]$ 。 提示？ 標準的な数学的分析では、この間隔のサイズが十分に長く減少すると、与えられた関数は非常にスムーズに動作し始め、直線、極端な場合は放物線で近似できるという事実に慣れています。 1715年に英国の科学者ブルックテイラーによって定式化された関数分解定理のおかげです。

$$

$$f（t + \ Delta t）= f（t）+ f '（t）\ cdot \ Delta t + \ frac {1} {2} f' '（t）\ cdot（\ Delta t）^ 2 + \ cdots$$

この定理は現代の数学者、エンジニアによって巧みに処理され、数値計算のためにすべてを一列に近似します。 しかし、フラクタルではそのようなスキームは失敗します。

ブノワマンデルブロが「フラクタル」という概念を思いついた頃には、多くの世界の科学者が100年間眠ることができませんでした。 フラクタルが評判を傷つけた最初の人の一人は、アンドレ・マリー・アンペアでした。 1806年、科学者は、任意の関数を連続関数の区間に分割できるというかなり説得力のある「証明」を提案しました。 そして彼の同時代の数学者の多くは彼に同意した。 一般に、アンペアは、この一見かなり粗雑なミスのせいにすることはできません。 19世紀初頭の数学者は、現在の数学的分析の基本概念を連続性と微分可能性としてやや曖昧に定義しており、その結果、彼らの証明は非常に誤っている可能性があります。 ガウス、フーリエ、コーシー、ルジャンドル、ガロアなどの著名な科学者も例外ではありませんでした。当時のあまり有名でない数学者は言うまでもありませんでした。

それにも関わらず、1872年、カール・ワイエルシュトラスは、どこでも微分可能で微分不可能な世界初のフラクタルモンスターを提示することにより、連続関数の派生物の存在の仮説に反論しました。

ここで、例えば、同様の機能がどのように設定されるか：

$$

$$f（t）= \ sum_ {n = 0} ^ \ infty \ frac {\ sin（2 ^ n t）} {2 ^ n}$$

ブラウン運動にも同じ特性があります（ちなみに、何らかの理由で、それはBrではなく Unovskyです。姓はイギリスですが、それでも）。 ブラウン運動は連続的なランダムプロセスです $$$B（t）$ すべての増分が独立しており、正規分布を持つように：

$$

$$B（T）-B（t）\ sim \ mathcal {N}（0、T-t）、\ quad t <T。$$

ブラウン運動の軌跡はフラクタル関数であり、どこでも連続的で滑らかではありません。 しかし、ワイエルシュトラス関数が単なる反例である場合、たとえそれが歴史全体で最も明るい数学的分析の1つであったとしても、ブラウン運動は確率論の基礎になると約束されており、どうにかしてそれを扱う方法を学ぶことが必要でした。

ブラウン運動の無限の変化

もう一度関数を想像してみましょう $$$f（t）$ 間隔で $$$t \ in [0、T]$ この間隔を多くの $$$n$ ばらばらの部分区間：

$$

$$\ Pi = \ {0 = t_0 <t_1 <\ dots <t_n = T \}。$$

ポイントがどのように分配されるかは気にしません $$$t_0、\ドット、t_n$ 、この間隔を分割すると、最大ステップのサイズはさらに興味深いものになります。 $$$\ | \ Pi \ | = \ max_ {i = 1、\ドット、n}（t_ {i} -t_ {i-1}）$ 数量を呼び出します

$$

$$V _ {[0、T]} ^ f = \ lim _ {\ | \ Pi \ | \右矢印0} \ sum_ {i = 1} ^ n | f（t_ {i}）-f（t_ {i-1}）|$$

（第一種）関数のバリエーション $$$f（t）$ （一般的なバリエーションとも呼ばれます）。 もし $$$V _ {[0、T]} ^ f <\ infty$ それから私たちはそれを言う $$$f（t）$ 有限のバリエーションがあります。 たとえば、十分に「滑らかな」関数のバリエーション

究極になります。 どちらの場合、私たちはそれほど確信が持てませんか？ たとえば、関数には最終的なバリエーションはありません

$$

$$f（t）= 1_ \ mathbb {Q}（t）、$$

帰る $$$1$ すべての合理的な $$$t$ そして $$$0$ すべての不合理な。 同様のロジックをランダム関数に拡張できます。 聞かせて $$$X（t）$ ランダムなプロセスです。 バリエーションは同じように設定されます：

$$

$$V _ {[0、T]} ^ X（\ omega）= \ lim _ {\ | \ Pi \ | \右矢印0} \ sum_ {i = 1} ^ n | X（t_ {i}）-X（t_ {i-1}）|（\ omega）。$$

唯一の違いは、バリエーションもランダムになることです（パラメーター $$$\オメガ$ 便宜上省略できますが、彼はここで、ランダムプロセスからの変動がランダムイベントの空間からのマッピングであることを示唆しています $$$\オメガ$ で $$$\ mathbb {R}$ ）

Haskellのバリエーションのかなり単純な実装は次のようになります。

-- | 'totalVariation' calculates total variation of the sample process X(t) totalVariation :: [Double] -- process trajectory X(t) -> Double -- V(X(t)) totalVariation x@(_:tx) = sum $ zipWith (\x xm1 -> abs $ x - xm1) tx x 

現実の世界では、ランダムプロセスはどこで発生しますか？ 今日の最も有名な例の1つは、金融市場、つまり通貨、株式、オプション、さまざまな証券の価格の動きです。 聞かせて $$$X（t）$ Appleシェアの価値です。 ある時点で、購入することにしました $$$f（t_0）$ 株価 $$$X（t_0）$ 、そして一定期間後、価格は変化し、等しくなりました $$$X（t_1）$ 。 その結果、あなたは $$$f（t_0）\ cdot \ Delta X（t_1）$ 純利益/損失、ここで $$$\デルタX（t_i）= X（t_i）-X（t_ {i-1}）$ 。 株式の一部を売買することを決定し、現在保有しています $$$f（t_1）$ 証券。 しばらくすると、あなたの収入/損失は $$$f（t_0）\ cdot \ Delta X（t_1）+ f（t_1）\ cdot \ Delta X（t_2）$ など 最後に、あなたが稼ぐ/失うことになります

$$

$$I（T）= \ sum_ {i = 1} ^ n f（t_ {i-1}）\ cdot \ Delta X（t_i）$$

すべてが非常に簡単ですが、ここにキャッチがあります：株式の価格を変更するプロセスは、それを売買するプロセス（いわゆる高頻度取引）のように、非常に迅速に移動できます。 私はこれらの計算を継続的なプロセスに拡張し、私たちの収入を $$$I（T）= \ int_0 ^ T f（t）dX（t）。$ 問題は、ランダムなプロセスとその軌跡を積分する方法がまだわからないことです。 しかし、標準のルベーグ積分（-Stieltjes）がどの原理で決定されるかを覚えています。 通常、最初に適切なメジャーを設定する必要があります。 減少しないプロセスをとる $$$X（t）$ 、簡単にするため、ゼロから始めます。 $$$X（0）= 0$ 、およびその増分に対応する非負のメジャー

$$

$$\ mu_X（a、b]：= X（b）-X（a）。$$

関数が $$$f（t）$ 限定的かつ測定可能（機能解析を思い出してください）、間隔で積分を決定できます $$$[0、T]$ 形で

$$

$$\ int_0 ^ T f（t）dX（t）= \ int _ {[0、T]} f（t）\ mu_X（dt）。$$

一般的なケースでは、ランダムプロセスの軌跡が単調でない場合、2つの非減少プロセスに分割できます。 $$$X（t）= X ^ +（t）-X ^-（t）、$ そして、ルベーグ積分を次のように定義します

$$

$$\ int_0 ^ T f（t）dX（t）= \ int _ {[0、T]} f（t）\ mu_ {X ^ +}（dt）-\ int _ {[0、T]} f（t ）\ mu_ {X ^-}（dt）。$$

そのような積分の存在の必要条件は、存在です $$$V _ {[0、T]} ^ X$ 。 実際、プロセスが2つの非減少プロセスの差で構成される場合、有限のばらつきがあります（2行目では、三角形の不等式を使用しました）。

$$

$$\ begin {aligned} V _ {[0、T]} ^ X＆= \ lim _ {\ | \ Pi \ | \右矢印0} \ sum_ {i = 1} ^ n | X（t_ {i}）-X（t_ {i-1}）| \\＆\ leq \ lim _ {\ | \ Pi \ | \ rightarrow 0} \ Big（\ sum_ {i = 1} ^ n | X ^ +（t_ {i}）-X ^ +（t_ {i-1}）| + \ sum_ {i = 1} ^ n | X ^-（t_ {i}）-X ^-（t_ {i-1}）| \ Big）\\＆= X ^ +（T）+ X ^-（T）<\ infty。 \ end {aligned}$$

ところで、この条件は逆方向にも機能します：プロセスがある場合 $$$X（t）$ 有限の変動で、次に決定できます $$$X ^ +（t）= \ frac {1} {2}（| X（t）| + X（t））$ そして $$$X ^-（t）= \ frac {1} {2}（| X（t）| -X（t））$ 。 単調さと平等 $$$X = X ^ +-X ^-$ 簡単に証明できます。

これで、簡単に何かを統合できます。 連続的なランダムプロセスの軌跡を取り、それを呼び出します $$$g（t）$ 。 ラグランジュ平均定理を使用して、連続関数について $$$g（t）$ 変動は等しくなります $$$V _ {[0、T]} ^ g = \ int_0 ^ T | g '（t）| dt$ 。 この積分が存在する場合、上記の有界性と測定可能性の条件下で $$$f（t）$ 私たちは数えることができます

$$

$$\ int_0 ^ Tf（t）dg（t）= \ int_0 ^ Tf（t）g '（t）dt。$$

これは本当に簡単です。 フラクタル、Weierstrassモンスターのような軌跡はどうですか？ 結局のところ、それらは存在しません $$$g '（t）$ 。



だから問題は：ブラウン運動のルベーグの意味で積分を取ることは可能か？ 変動を計算し、それが有限であれば、問題はないはずです。 いわゆる二次変動の側面から見てみましょう。

$$

$$[B]（T）= \ lim _ {\ | \ Pi \ | \右矢印0} \ sum_ {i = 1} ^ n \ big（B（t_ {i + 1}）-B（t_i）\ big）^ 2$$

この制限は何に等しいと思いますか？ 確率変数を考えます $$$[B]（T）-T$ そして、その分散がゼロであることを示します。

$$

$$\ begin {aligned} \ sum_ {i = 1} ^ n \ big（B（t_ {i + 1}）-B（t_i）\ big）^ 2-T＆= \ sum_ {i = 1} ^ n \ Big（\ big（B（t_ {i + 1}）-B（t_i）\ big）^ 2-（t_ {i + 1} -t_i）\ Big）\\＆= \ sum_ {i = 1} ^ n（Z_i ^ 2-1）（t_ {i + 1} -t_i）、\ end {aligned}$$

どこで

$$

$$Z_i = \ frac {B（t_ {i + 1}）-B（t_i）} {\ sqrt {t_ {i + 1}-t_i}} \ sim \ mathcal {N}（0,1）$$

標準正規分布値。 特に、すべての $$$Z_i ^ 2$ 独立しており、次数1のカイ二乗分布を持っているため、簡単に計算できます

$$

$$\ mathbb {E} [（Z_i ^ 2-1）^ 2] = \ operatorname {Var}（Z_i ^ 2）= 2$$

だから

$$

$$\ begin {aligned} \ mathbb {E} \ bigg [\ Big（\ sum_ {i = 1} ^ n \ big（B（t_ {i + 1}）-B（t_i）\ big）^ 2 -T \ Big）^ 2 \ bigg]＆= \ sum_ {i = 1} ^ n \ mathbb {E} [（Z_i ^ 2-1）^ 2（t_ {i + 1} -t_i）^ 2] \\＆ = 2 \ sum_ {i = 1} ^ n（t_ {i + 1} -t_i）^ 2 \\＆\ leq \ | \ Pi \ | \ cdot 2 \ sum_ {i = 1} ^ n（t_ {i + 1} -t_i）\右矢印0. \ end {aligned}$$

言い換えれば、

$$

$$[B]（T）=T。$$

この式を覚えておいてください！ これは確率的分析の基礎であり、中心極限定理の特異な局所類似体であり、他のすべての定理は明示的および暗示的にそれを中心に展開します。

に注意してください $$$[B]（T）= \ operatorname {Var}（B（T））$ ただし、これら2つの量の計算方法は完全に異なります。 ブラウン運動の分散は、確率を考慮して、そのすべての軌道の平均化と見なされます。 二次変動は、それに沿って動きが発生した単一のランダムな軌跡から取得され、確率はここでは役割を果たしません。 分散は理論的にしか計算できませんが、すべての実装の平均化が必要なため、二次実装は明示的に計算できます（十分なデータ離散化を使用）。 上記の式は、定義上、第1種の変動のような2次変動であるという点で特に興味深い $$$V _ {[0、T]} ^ X$ ランダム変数です。 ただし、ブラウン運動の特徴は、運動がどの軌跡をとったかに関係なく 、その二次変動が縮退し、間隔の長さに対応する単一の値のみをとることです。

ランダムプロセスの実装の二次変動を考慮するコードを書きましょう $$$X（t）$ ：

 -- | 'quadraticVariation' calculates quadratic variation of the sample process X(t) quadraticVariation :: [Double] -- process trajectory X(t) -> Double -- [X(t)] quadraticVariation x@(_:tx) = sum $ zipWith (\x xm1 -> (x - xm1) ^ 2) tx x 

これで、関心のある変動の計算に戻る準備ができました。 $$$V _ {[0、T]} ^ B$ 。 わかった

$$

$$\ lim _ {\ | \ Pi \ | \ rightarrow 0} \ sum_ {i = 1} ^ n（B（t_ {i + 1}）-B（t_i））^ 2 = T.$$

つまり、ゼロ以外の値ですが、無限値ではありません。 一方、それは上から壊れたの最大ステップによって区切られます $$$B（t）$ ：

$$

$$\ begin {aligned} \ sum_ {i = 1} ^ n（B（t_ {i + 1}）-B（t_i））^ 2 \ leq \ max \ big \ {| B（t_ {i + 1} ）-B（t_i）| \ビッグ| （t_ {i}、t_ {i + 1}）\サブセット\ Pi \ビッグ\} \ cdot \ sum_ {i = 1} ^ n | B（t_ {i + 1}）-B（t_i）| 。 \ end {aligned}$$

ブラウン運動は連続的なプロセスであり、つまり

$$

$$\ max \ big \ {| B（t_ {i + 1}）-B（t_i）| \ビッグ| （t_ {i}、t_ {i + 1}）\サブセット\ Pi \ビッグ\} \右矢印0$$

しかし $$$\ sum_ {i = 1} ^ n | B（t_ {i + 1}）-B（t_i）| \右矢印V _ {[0、T]} ^ B.$ そして、その結果、

$$

$$V _ {[0、T]} ^ B = \ infty。$$

そうそう...

伊藤インテグラルまたはニューホープ

1827年、英国の植物学者ロバート・ブラウンは、顕微鏡で水中の花粉粒を観察し、その空洞内の粒子が特定の方法で動くことに気付きました。 しかし、その後、彼はこの運動を引き起こしたメカニズムを特定することができませんでした。 1905年、アルバート・アインシュタインは、ブラウンによって観察された動きが、個々の水分子による花粉の動きの結果である方法を詳細に説明する記事を発表しました。 1923年、子供の天才であり「サイバネティックスの父」であるノルベルト・ウィナーは微分可能空間に関する記事を書き、数学の側面からこの動きにアプローチし、軌跡の空間における確率尺度を決定し、ルベーグ積分の概念を使用して、確率的分析の基礎を築きました。 それ以来、数学的コミュニティでは、ブラウン運動はウィーナー過程とも呼ばれています。

1938年、東京大学を卒業した伊藤清は統計局で働き始め、余暇に彼は現代確率理論の創始者アンドレイ・コルモゴロフと当時のブラウン運動のさまざまな特性を研究していたフランスの科学者ポール・レヴィの仕事に精通した。 彼は、レヴィの直感的なビジョンとコルモゴロフの正確な論理を組み合わせようとし、1942年に「確率過程と無限に可分な分布則」について書きます。彼は、確率積分の概念と、関連する確率微分方程式の理論をゼロから再構築しますランダムなイベント。

シンプルなプロセスのための伊藤積分

伊藤は、積分を構築するかなり簡単な方法を開発しました。 まず、単純な区分的定数プロセスの伊藤積分を定義します $$$\デルタ（t）$ そして、この概念をより複雑な被積分関数に拡張します。 もう一度分割しましょう $$$\ Pi = \ {0 = t_0 <t_1 <\ dots <t_n = T \}$ 。 私たちは価値観 $$$\デルタ（t）$ 各間隔で一定 $$$[t_j、t_ {j + 1}）$

想像してみて $$$B（t）$ 当時の金融商品の価値 $$$t$ （ブラウンの動きは負の値を取ることができるため、これは価格の動きの良いモデルではありませんが、今は無視します）。 みましょう $$$t_0、t_1、\ドット、t_ {n-1}$ -これらは取引日です（時間/秒、それは重要ではありません）、そして $$$\デルタ（t_0）、\デルタ（t_1、）、\ドット、\デルタ（t_ {n-1}）$ -これは私たちの立場（手元にある金融商品の数）です。 私たちは $$$\デルタ（t）$ その時点で知られている情報のみに依存する $$$t$ 。 情報とは、この時点までのブラウン運動の軌跡を意味します。 その後、私たちの収入は次のようになります。

$$

$$I（t）= \ sum_ {j = 0} ^ k \ Delta（t_j）[B（t_ {j + 1} -B（t_j）] + \ Delta（t_k）[B（t）-B（t_k ）]。$$

プロセス $$$I（t）$ 単純なプロセスのito積分と呼ばれる $$$\デルタ（t）$ そして、私たちはそれを次の形式で書きます

$$

$$I（t）= \ int_0 ^ t \ Delta（s）dB（s）。$$

この積分にはいくつかの興味深い特性があります。 最初の、そしてかなり明白なこと：最初の瞬間では、任意の点での数学的な期待はゼロです：

$$

$$\ mathbb {E} [I（t）] =0。$$

さらに、伊藤積分はマルチンゲールですが、それについては後で詳しく説明します。

二次モーメント/分散の計算には、すでに追加の計算が必要です。 聞かせて $$$D_j = B（t_ {j + 1}）-B（t_j）$ のために $$$j = 1、\ドット、k-1$ そして $$$D_k = B（t）-B（t_k）$ 。 次に、伊藤積分を次の形式で書き換えます。

$$

$$I（t）= \ sum_ {j = 0} ^ k \ Delta（t_j）D_j$$

という事実を利用して $$$\ mathbb {E} [D_j] = 0$ そしてその事実 $$$D_j$ そして $$$D_i$ 独立した $$$i \ neq j$ 計算できます

$$

$$\ begin {aligned} \ mathbb {E} [I ^ 2（t）]＆= \ mathbb {E} \ Big [\ sum_ {j = 0} ^ k \ Delta ^ 2（t_j）D_j ^ 2 + 2 \ sum_ {0 \ leq i <j \ leq k} \ Delta（t_i）\ Delta（t_j）D_iD_j \ Big] \\＆= \ sum_ {j = 0} ^ k \ mathbb {E} \ Big [\ Delta ^ 2（t_j）D_j ^ 2 \ Big] + 2 \ sum_ {0 \ leq i <j \ leq k} \ mathbb {E} [\ Delta（t_i）\ Delta（t_j）D_iD_j] \\＆= \ sum_ {j = 0} ^ k \ mathbb {E} \ Big [\ Delta ^ 2（t_j）\ Big] \ cdot \ mathbb {E} [D_j ^ 2] + 2 \ sum_ {0 \ leq i <j \ leq k} \ mathbb {E} [\ Delta（t_i）\ Delta（t_j）D_i] \ cdot \ mathbb {E} [D_j] \\＆= \ sum_ {j = 0} ^ {k-1} \ mathbb { E} \ Big [\ Delta ^ 2（t_j）\ Big]（t_ {j + 1} -t_j）+ \ mathbb {E} [\ Delta ^ 2（t_k）]（t-t_k）\\＆= \ sum_ {j = 0} ^ k \ mathbb {E} \ Big [\ int_ {t_j} ^ {t_ {j + 1}} \ Delta ^ 2（s）ds \ Big] + \ mathbb {E} \ Big [ \ int_ {t_k} ^ t \ Delta ^ 2（s）ds \ Big] \\＆= \ mathbb {E} \ Big [\ int_ {0} ^ t \ Delta ^ 2（s）ds \ Big]。 \ end {aligned}$$

平等

$$

$$\ mathbb {E} [I ^ 2（t）] = \ mathbb {E} \ Big [\ int_0 ^ t \ Delta ^ 2（s）ds \ Big]$$

伊藤アイソメと呼ばれる。

そして最後に、二次変動。 最初に各間隔の変動を計算しましょう $$$[t_j、t_ {j + 1}]$ 値 $$$\デルタ（t）$ 定数であり、それらをすべてまとめます。 分割間隔をとる $$$t_j = s_0 <s_1 <\ cdots <s_m = t_ {j + 1}$ そして検討する

$$

$$\ begin {aligned} \ sum_ {i = 0} ^ {m-1} [I（s_ {i + 1}）-I（s_i）] ^ 2＆= \ sum_ {i = 0} ^ {m- 1} [\ Delta（t_j）（B（s_ {i + 1}）-B（s_i））^ 2 \\＆= \ Delta ^ 2（t_j）\ sum_ {t = 0} ^ {m-1} （B（s_ {i + 1}）-B（s_i））^ 2 \\＆\ xrightarrow [m \ rightarrow \ infty] {} \ Delta ^ 2（t_j）（t_ {j + 1} -t_j）\ \＆= \ int_ {t_j} ^ {t_ {j + 1}} \ Delta ^ 2（s）ds。 \ end {aligned}$$

同様に、区間の二次変動が考慮されます $$$[t_k、t]$ 。 これらすべてを要約すると、

$$

$$[I（t）] = \ int_0 ^ t \ Delta ^ 2（s）ds。$$

これで、分散と変動の違いを明確に見ることができます。 プロセスが $$$\デルタ（t）$ 決定的である場合、それらは一致します。 しかし、ブラウン運動が通過した軌道に応じて戦略を変更することにした場合、変動は常に変化し始めますが、分散は常に特定の値に等しくなります。

複雑なプロセスのための伊藤積分

これで、伊藤積分の概念をより複雑なプロセスに拡張する準備ができました。 機能を持ってみましょう $$$h（t）$ 、時間の経過とともに絶えず変化する可能性があり、ギャップもあります。 維持したい唯一の仮定は、二次プロセスの可積分性です。

$$

$$\ mathbb {E} \ Big [\ int_0 ^ T h ^ 2（t）dt \ Big] <\ infty$$

そして適応性 、すなわち 当時 $$$t$ 意味がわかったら $$$B（t）$ 私たちはすでに意味を知っているはずです $$$h（t）$ 。 現実の世界では、明日の株式の価値を最初に見つけてから投資することはできません。

決定するために $$$\ int_0 ^ T h（t）dB（t）$ おおよそ $$$h（t）$ 簡単なプロセス。 以下のグラフは、これを行う方法を示しています。


近似は次のとおりです。パーティションを選択します $$$0 = t_0 <t_1 <t_2 <t_3$ 、次に値が等しい単純なプロセスを作成します $$$h（t_j）$ それぞれについて $$$t_j$ セグメント上で変更しないでください $$$[t_j、t_ {j + 1}）$ 。 パーティションの最大ステップが小さくなると、近似する単純なプロセスが被積分関数に近くなります。

一般に、一連の単純なプロセスを選択することが可能です $$$h_n（t）$ に収束するように $$$h（t）$ 。 収束とは

$$

$$\ lim_ {n \ rightarrow \ infty} \ mathbb {E} \ Big [\ int_0 ^ T | h_n（t）-h（t）| ^ 2 dt \ Big] = 0$$

すべてのプロセスについて $$$h_n（t）$ 伊藤積分は既に定義されており、絶えず変化するプロセスの限界として伊藤積分を定義しています。

$$

$$\ int_0 ^ t h（s）dB（s）= \ lim_ {n \ rightarrow \ infty} \ int_0 ^ th_n（s）dB（s）、\ quad 0 \ leq t \ leq T.$$

一般的な場合の伊藤積分には、次の特性があります。

• その軌跡は連続的です
• それは適応されます。 収入の価値を常に知っていなければならないので、それは論理的です。
• それは線形です： $$$\ int_0 ^ t h（s）dB（s）+ \ int_0 ^ t f（s）dB（s）= \ int_0 ^ t（h（s）+ f（s））dB（s）$
• 彼はマーチンゲールですが、それについては記事の終わり近くで詳しく説明しています。
• 保存されたIso Itometry： $$$\ mathbb {E} [I ^ 2（t）] = \ mathbb {E} \ Big [\ int_0 ^ t h ^ 2（s）ds \ Big]$ 。
• その二次変動： $$$[I（t）] = \ int_0 ^ th ^ 2（s）ds。$

ちょっとしたコメント：伊藤積分の構築をより詳細に研究したい、または一般的に金融数学に興味がある人のために、Steven Shreveの著書「Stochastic Calculus for Finance。 ボリュームII "。

行こう？

次の理由から、伊藤積分をわずかに異なる形式で示します。

$$

$$I（h）= \ int_ {0} ^ T h（s）dB（s）、$$

いくつかのために $$$T$ 。 したがって、伊藤積分は二次的に積分可能な関数の空間から作用するマップであるという考えに備えます $$$L ^ 2（[0、T]）$ ランダムプロセスの確率空間に。 したがって、たとえば、古い表記法から新しい表記法に移行できます。

$$

$$I（t）= \ int_0 ^ T h（s）\ cdot 1 _ {[0、t]}（s）ds = I（h \ cdot 1 _ {[0、t]}）$$

前の記事では、ガウス過程を実装しました。 $$$W：H \右矢印L ^ 2（\ Omega、\ mathcal {F}、\ mathbb {P}）$ 。 ガウス過程はヒルベルト空間から確率空間へのマッピングであり、これは基本的に伊藤積分の一般化されたケースであり、関数の空間からランダムなプロセスの空間へのマッピングです。 確かに

 data L2Map = L2Map {norm_l2 :: Double -> Double} type ItoIntegral = Seed -- ω, random state -> Int -- n, sample size -> Double -- T, end of the time interval -> L2Map -- h, L2-function -> [Double] -- list of values sampled from Ito integral -- | 'itoIntegral'' trajectory of Ito integral on the time interval [0, T] itoIntegral' :: ItoIntegral itoIntegral' seed n endT h = 0 : (toList $ gp !! 0) where gp = gaussianProcess seed 1 (n-1) (\(i, j) -> norm_l2 h $ fromIntegral (min ij + 1) * t) t = endT / fromIntegral n 

itoIntegral関数は、 シードを入力として受け取ります-ランダムジェネレーターのパラメーター、 n-出力ベクトルの次元、 endT-パラメーター $$$T$ そして、被積分関数のノルムを返すnorm_l2関数が定義されているL2Mapクラスの関数h ： $$$t \ mapsto \ int_0 ^ t h ^ 2（s）ds$ 。 出力で、 itoIntegralは、間隔にIto積分の実装を発行します $$$[0、T]$ パラメータnに対応するサンプリングレート。 当然、伊藤積分を実装する同様の方法は、ある意味では行き過ぎです。しかし、それは、あなたがさらなる考察のためにとても必要な機能的思考に同調することを可能にします。 巨大なマトリックスでの作業を必要としない、より高速な実装を作成します。

 -- | 'mapOverInterval' map function f over the interval [0, T] mapOverInterval :: (Fractional a) => Int -- n, size of the output list -> a -- T, end of the time interval -> (a -> b) -- f, function that maps from fractional numbers to some abstract space -> [b] -- list of values f(t), t \in [0, T] mapOverInterval n endT fn = [fn $ (endT * fromIntegral i) / fromIntegral (n - 1) | i <- [0..(n-1)]] -- | 'itoIntegral' faster implementation of itoIntegral' function itoIntegral :: ItoIntegral itoIntegral seed 0 _ _ = [] itoIntegral seed n endT h = scanl (+) 0 increments where increments = toList $ (sigmas hnorms) * gaussianVector gaussianVector = flatten $ gaussianSample seed (n-1) (vector [0]) (H.sym $ matrix 1 [1]) sigmas s@(_:ts) = fromList $ zipWith (\xy -> sqrt(xy)) ts s hnorms = mapOverInterval n endT $ norm_l2 h 

ここで、この関数を使用して、たとえば通常のブラウン運動を実装できます。 $$$B（t）= \ int_0 ^ t dB（s）$ 。 関数hは、そのノルムnorm_l2が $$$t \ mapsto \ int_0 ^ t ds = t$ 同じ機能。

 l2_1 = L2Map {norm_l2 = id} -- | 'brownianMotion' trajectory of Brownian motion aka Wiener process on the time interval [0, T] brownianMotion :: Seed -- ω, random state -> Int -- n, sample size -> Double -- T, end of the time interval -> [Double] -- list of values sampled from Brownian motion brownianMotion seed n endT = itoIntegral seed n endT l2_1 

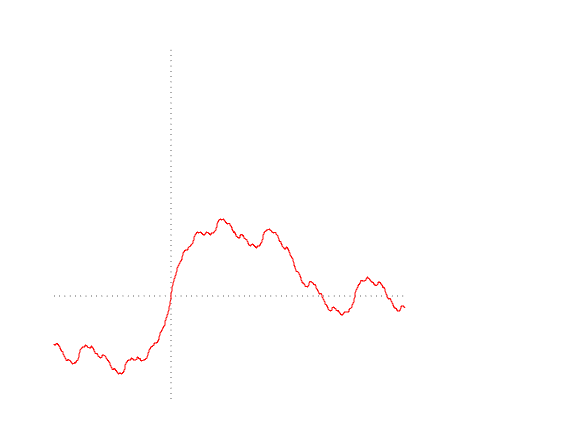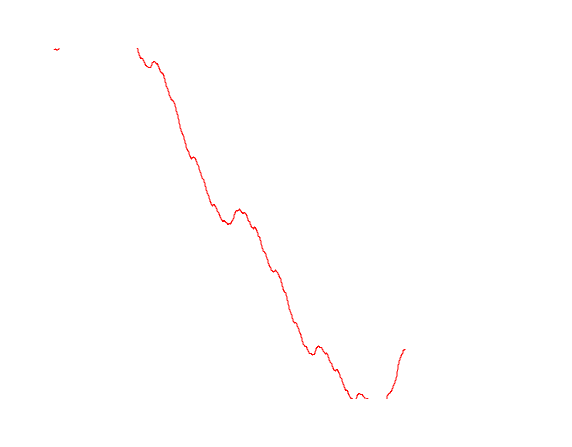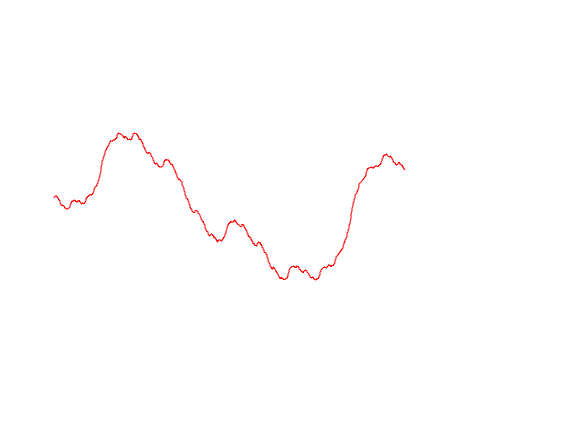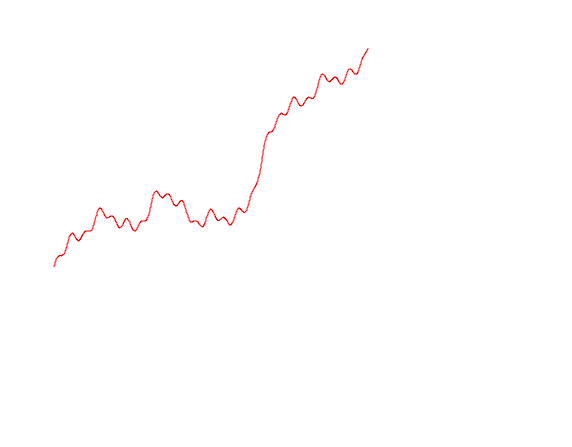
ブラウン運動の軌跡にさまざまなオプションを描画してみましょう

 import Graphics.Plot let endT = 1 let n = 500 let b1 = brownianMotion 1 n endT let b2 = brownianMotion 2 n endT let b3 = brownianMotion 3 n endT mplot [linspace n (0, lastT), b1, b2, b3] 

今度は、以前の計算を再確認します。 区間のブラウン運動軌道の変化を計算しましょう $$$[0、1]$ 。

 Prelude> totalVariation (brownianMotion 1 100 1) 8.167687948236862 Prelude> totalVariation (brownianMotion 1 10000 1) 80.5450335433388 Prelude> totalVariation (brownianMotion 1 1000000 1) 798.2689137110999 

精度を上げると、変動はますます大きな値をとることになりますが、二次変動は $$$T = 1$ ：

 Prelude> quadraticVariation (brownianMotion 1 100 1) 0.9984487348804609 Prelude> quadraticVariation (brownianMotion 1 10000 1) 1.0136583395467458 Prelude> quadraticVariation (brownianMotion 1 1000000 1) 1.0010717246843375 

任意のIto積分の変動の計算を実行して、次のことを確認してください。 $$$[I]（h）= \ int_0 ^ T h ^ 2（s）ds$ 動きの軌跡に関係なく。

マーティンゲールズ

そのようなクラスのランダムプロセス- マルチンゲールがあります。 するために $$$X（t）$ マーチンゲールであった場合、3つの条件を満たしている必要があります。

• それは適応されます
• $$$X（t）$ もちろんほぼどこでも：

  $$

  $$\ mathbb {E} [| X（t）|] <\ infty$$
• 将来価値に対する条件付きの数学的期待 $$$X（t）$ 最後の既知の値に等しい：

  $$

  $$\ mathbb {E} [X（T）| X（t）] = X（t）、\ quad t <T。$$

ブラウン運動-マーチンゲール。 最初の条件の充足は明らかであり、2番目の条件の充足は正規分布の特性に基づいています。 3番目の条件も簡単に確認できます。

$$

$$\ mathbb {E} [B（T）| B（t）] = \ mathbb {E} [（B（T）-B（t））+ B（t）| B（t）] = B（t ）。$$

伊藤積分もマーチンゲールです（練習問題として証明を残しましょう）。 これは何を教えてくれますか？ 金融数学に戻り、選択した株式の価値がブラウン運動であると想像してみましょう（仮定はかなり単純ですが、それでも想像してみてください）。 $$$h（t）$ -これは当社の戦略であり、ポートフォリオの株式数です。 プロセス $$$h（t）$ ランダムである可能性があります：保有する在庫の数を常に事前に把握しているとは限らないため、価格変動から先に進みます $$$B（t）$ 。 しかし、主なことは、このプロセスを適応させることです。つまり、 $$$t$ 在庫数を正確に把握しています。 過去に戻ってこの意味を変えることはできません。 伊藤積分はマルチンゲールなので、どの戦略を選択しても問題ありません $$$h（t）$ 、平均して、私たちの取引からの利益は常にゼロになります。

別の興味深い定理、いわゆるマルチンゲール表現定理があります。マルチンゲールがある場合 $$$M（t）$ その値はブラウン運動によって決定されます。つまり、値に不確実性を導入する唯一のプロセスです。 $$$M（t）$ は $$$B（t）$ このマルチンゲールは次のように表すことができます

$$

$$M(t) = M(0) + \int_0^t H(s)dB(s),$$

さらに、プロセス $$$H(s)$唯一のもの。将来、積分の数を増やし、さらにそれらを非適応プロセスにまで拡張する場合、この定理は私たちに大いに役立ちます。

そしてそれが今日のすべてです。