最大の増加サブシーケンスの長さを見つける問題を解決します

内容：

フィボナッチ数列O（n）
Oのソリューション（n ^ 2）
バイナリ検索O（log n）
Oのソリューション（n * log n）

挑戦する

「配列内の最大の昇順サブシーケンスの長さを見つけます。」

一般に、これは2つのシーケンスの共通要素を見つける問題の特殊なケースです。2番目のシーケンスは同じシーケンスで、ソートされているだけです。

指に

シーケンスがあります：

5、10、6、12、3、24、7、8

サブシーケンスの例を次に示します。

10、3、8
5、6、3

そして、サブシーケンスの増加の例を次に示します。

5、6、7、8
3、7、8

そして、最大長のサブシーケンスを増やす例は次のとおりです。

5、6、12、24
5、6、7、8

はい、多くの上限があります。長さにのみ関心があります。
ここは4です。

問題が定義されたので、フィボナッチ数の計算は（動的なプログラミング）を使用する最も単純なアルゴリズムであるため、フィボナッチ数の計算によって解決し始めます。 DPは個人的には正しい関連付けを引き起こさない用語です。このアプローチは、「同じタスクのより小さな次元の中間結果を保持しながらプログラミングする」と呼びます。 ただし、蒸したカブよりもDPを使用してフィボナッチ数を計算する方が簡単な場合は、次のパートに進んでください。 フィボナッチ数自体はサブシーケンスの元の問題とは関係ありません。DPの原理を示したいだけです。

フィボナッチ数列O（n）

フィボナッチ数列は人気があり、伝説に囲まれています。彼らは可能な限りそれを見ようとします（そして、私たちはそれをなんとかすることができます）。 その原理は単純です。 シーケンスのn番目の要素は、n-1要素とn-2要素の合計です。 それぞれ0と1で始まります。

0、1、1、2、3、5、8、13、21、34 ...

0を取り、1を足します。
1、1を追加-2を取得します。
1を取り、2を足します。わかります、3。

実際に、このシーケンスのn番目の要素を見つけることがタスクになります。 解決策は、このシーケンスのまさに定義にあります。 フィボナッチ数の計算の中間結果を保存する1つの可変配列を作成します。 同じn-1とn-2。

擬似コード：

int numberForIndex(int index) { int[] numbers = [0, 1]; //  ,      for (int i = 2; i < index + 1; i++) { numbers[index] = numbers[i - 1] + numbers[i - 2]; } return numbers[index]; } 

→ Objective-Cのソリューション例

→ テスト

それだけです。この数値配列では、DPソルトはすべて一種のキャッシュ（Cahe）であり、同じタスクの以前の計算結果を小さな次元（n-1およびn-2）でのみ追加します。次元nの解を見つけるための1つのアクション。

このアルゴリズムはO（n）で機能しますが、少し余分なメモリ（配列）を使用します。

最大増加サブシーケンスの長さを見つけることに戻りましょう。

Oのソリューション（n ^ 2）

次のサブシーケンスの増加を検討してください。

5、6、12

次に、シーケンスの最後の要素の後の次の番号を見てみましょう。これは3です。

それは私たちのシーケンスの継続でしょうか？ いや 12未満です。

24はどうですか？

はい、できます。

したがって、シーケンスの長さは3 + 1になり、シーケンスは次のようになります。

5、6、12、24

そこで、以前の計算を再利用します。5、6、12のサブシーケンスがあり、長さは3であり、24を簡単に追加できるようになったことがわかりました。

別の追加の配列（ここではキャッシュ、ここではDP）を取得して、n番目の要素の増加するサブシーケンスのサイズを格納します。

次のようになります。

私たちのタスクは、counts配列に正しい値を入力することです。 各要素自体が最小の増加サブシーケンスであるため、最初はユニットで満たされています。

「どんな神秘的なiとj？」とあなたは尋ねます。 これらは、使用する配列の反復子のインデックスです。 それらは、2つのサイクルを使用して変更されます。 私は常にj未満になります。

jは10を見ています。これは、彼に到達するシーケンスのメンバーの候補です。 私がどこにいるのか見てみましょう、5があります。

10は5より大きく、1 <= 1、カウント[j] <=カウント[i]？ はい、それはカウント[j] =カウント[i] + 1を意味します。最初に私たちの推論を覚えていますか？

これで、テーブルは次のようになります。

シフトj

結果：

この表を目の前に置いて、どのステップを実行する必要があるかを理解すると、これをコードで簡単に実装できます。

 int longestIncreasingSubsequenceLength( int numbers[] ) { if (numbers.count == 1) { return 1; } int lengthOfSubsequence[] = rray.newArrayOfSize(numbers.count, 1); for (int j = 1; j < numbers.count; j++) { for (int k = 0; k < j; k++) { if (numbers[j] > numbers[k]) { if (lengthOfSubsequence[j] <= lengthOfSubsequence[k]) { lengthOfSubsequence[j] = lengthOfSubsequence[k] + 1; } } } } int maximum = 0; for (int length in lengthOfSubsequence) { maximum = MAX(maximum, length); } return maximum; } 

→ Objective-Cでの実装
→ テスト

コード内の2つのネストされたループを見逃すことはできません。また、同じ配列を通過する2つのネストされたループがある場合、2次複雑度O（n ^ 2）があります。

今、あなたがバイリンガルなら、間違いなく「私たちはもっと良くできますか？」と疑問に思うでしょう、普通の人間は「これをもっと短時間で行うアルゴリズムを考え出すことができますか？」

回答：「はい、できます！」

これを行うには、バイナリ検索とは何かを覚えておく必要があります。

バイナリ検索O（log n）

バイナリ検索は、ソートされた配列でのみ機能します。 たとえば、ソートされた配列で番号nの位置を見つける必要があります。
1、5、6、8、14、15、17、20、22

配列が並べ替えられていることを知っているので、配列内の特定の数の右または左に、必要な数を常に指定できます。

この配列の8番の位置を探しています。 アレイの中央からどちら側になりますか？ 14は配列の中央の数字です。 8 <14-したがって8の14の左側。これで、配列の右側の部分に関心がなくなり、8につまずくまでそれをドロップして同じ操作を何度も繰り返すことができます。ご覧のとおり、配列のすべての要素を調べる必要はありません、このアルゴリズムの複雑さは<O（n）であり、O（log n）と等しくなります。

アルゴリズムを実装するには、インデックスに3つの変数、left、middle、rightが必要です。

番号8の位置を探しています。

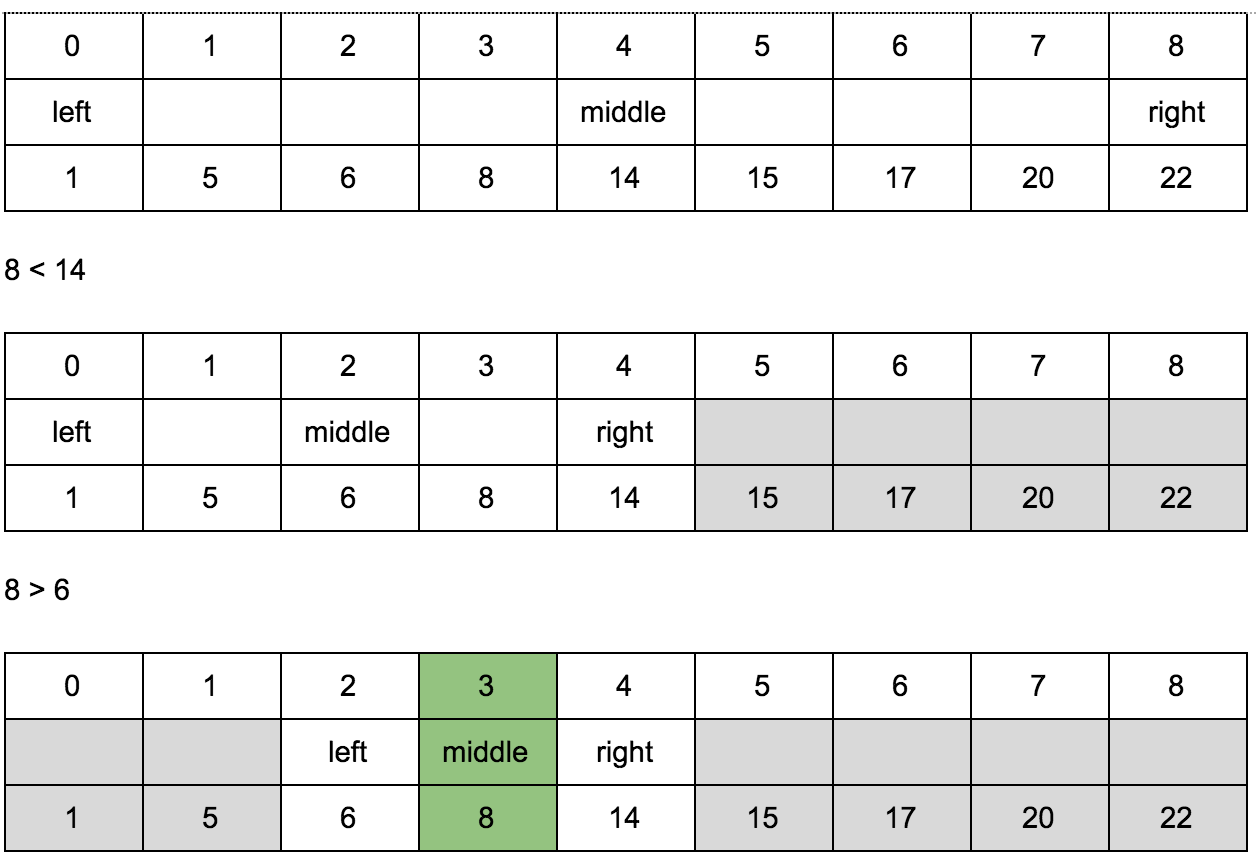
3つの音符から8がどこにあるか推測しました。

 int binarySearch(int list [], int value) { if !list.isEmpty { int left = list.startIndex int right = list.endIndex-1 while left <= right { let middle = left + (right - left)/2 if list[middle] == value{ return middle } if value < list[middle]{ right = middle - 1 } else{ left = middle + 1 } } } return nil } 

Oのソリューション（n * log n）

ここで、元の配列を調べながら、新しい配列に入力します。この配列には、増加するサブシーケンスが格納されます。 このアルゴリズムのもう1つの利点：最大増加サブシーケンスの長さだけでなく、サブシーケンス自体も検出します。

バイナリ検索は、サブシーケンスの配列をどのように取り込むのに役立ちますか？

このアルゴリズムを使用して、補助配列内の新しい要素の場所を探します。ここでは、サブシーケンスの長さごとに、終了できる最小要素を格納します。

要素が配列の最大要素より大きい場合、要素を最後に追加します。 簡単です。

そのような要素が既に配列に存在する場合、実際には何も変わりません。 それも簡単です。

考慮する必要があるのは、次の要素がこの配列の最大値より小さい場合です。 最後に入れることはできないことは明らかであり、正確に最大シーケンスのメンバーである必要はありません。逆もまた同様です。現在持っているサブエレメントで、この新しい要素を含まないサブシーケンスは最大ではない場合があります。

これは混乱を招きますが、今では簡単になり、残りの2つのケースを考慮に入れます。

1. シーケンスの考慮される要素（x）は、配列の最大要素（Nmax）よりも小さいが、最後から2番目の要素よりも大きい。
2. 問題の要素は、配列の中央にあるいくつかの要素よりも小さいです。

ケース1では、単純に配列内にNmaxをスローし、その場所にxを配置できます。 後続の要素がNmaxを超える場合、xを超えることは明らかであるため、単一の要素が失われることはありません。

ケース2：このケースが役立つように、この要素が最大になるサブシーケンスのサイズを格納する別の配列を作成します。 実際、このサイズは、この要素の最初の補助配列内の位置になります。これは、バイナリ検索を使用して検索します。 目的の位置が見つかったら、その右側の要素を確認し、現在の位置が小さい場合は現在の位置に置き換えます（ここでは、最初の場合と同じロジックが機能します）

このテキストの説明からすべてが明確になったわけではない場合、がっかりしないでください。

必要なもの：

1. ソースシーケンス
2. 可変配列を作成し、サブシーケンスの増加要素を保存します
3. 問題の要素が最大になるサブシーケンスサイズの可変配列を作成します。

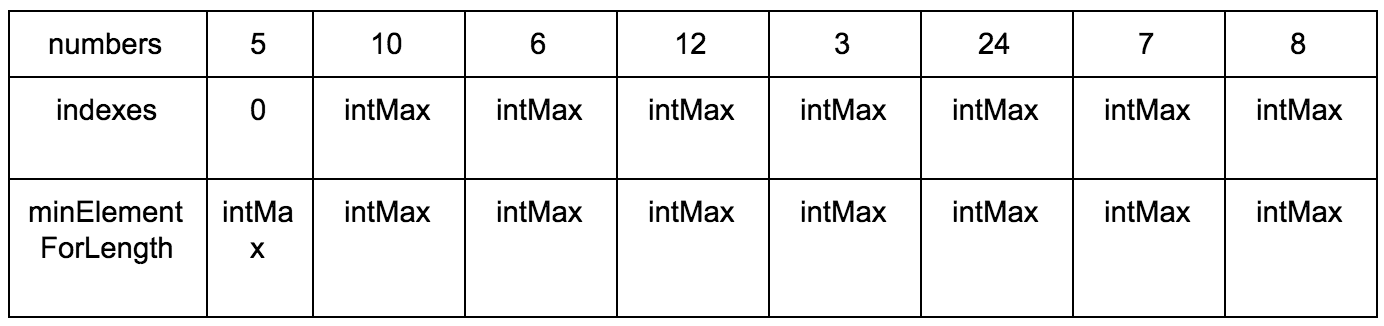
結果：

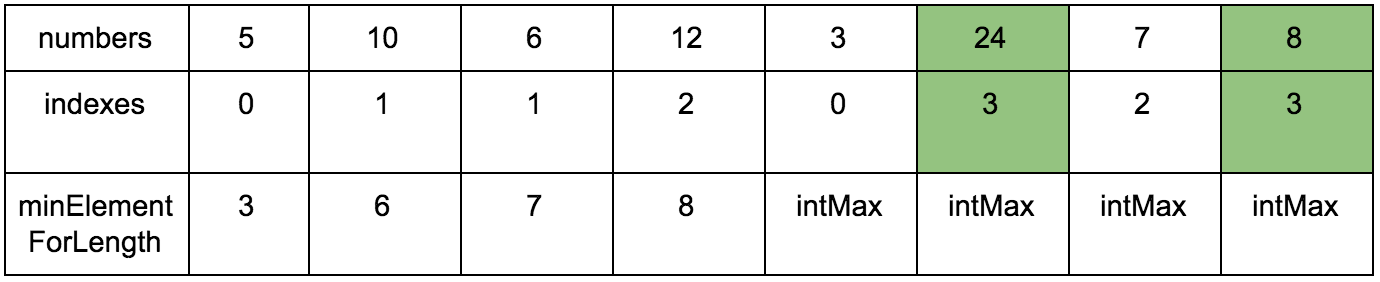
 int longestIncreasingSubsequenceLength(int numbers[]) { if (numbers.count <= 1) { return 1; } int lis_length = -1; int subsequence[]; int indexes[]; for (int i = 0; i < numbers.count; ++i) { subsequence[i] = INT_MAX; subsequence[i] = INT_MAX; } subsequence[0] = numbers[0]; indexes[0] = 0; for (int i = 1; i < numbers.count; ++i) { indexes[i] = ceilIndex(subsequence, 0, i, numbers[i]); if (lis_length < indexes[i]) { lis_length = indexes[i]; } } return lis_length + 1; } int ceilIndex(int subsequence[], int startLeft, int startRight, int key){ int mid = 0; int left = startLeft; int right = startRight; int ceilIndex = 0; bool ceilIndexFound = false; for (mid = (left + right) / 2; left <= right && !ceilIndexFound; mid = (left + right) / 2) { if (subsequence[mid] > key) { right = mid - 1; } else if (subsequence[mid] == key) { ceilIndex = mid; ceilIndexFound = true; } else if (mid + 1 <= right && subsequence[mid + 1] >= key) { subsequence[mid + 1] = key; ceilIndex = mid + 1; ceilIndexFound = true; } else { left = mid + 1; } } if (!ceilIndexFound) { if (mid == left) { subsequence[mid] = key; ceilIndex = mid; } else { subsequence[mid + 1] = key; ceilIndex = mid + 1; } } return ceilIndex; } 

→ Objective-Cでの実装
→ テスト

まとめ

さまざまな複雑さの4つのアルゴリズムを確認しました。 これらは、アルゴリズムを分析するときに常に対処しなければならない困難です。

O（log n）、O（n）、O（n * log n）、O（n ^ 2）

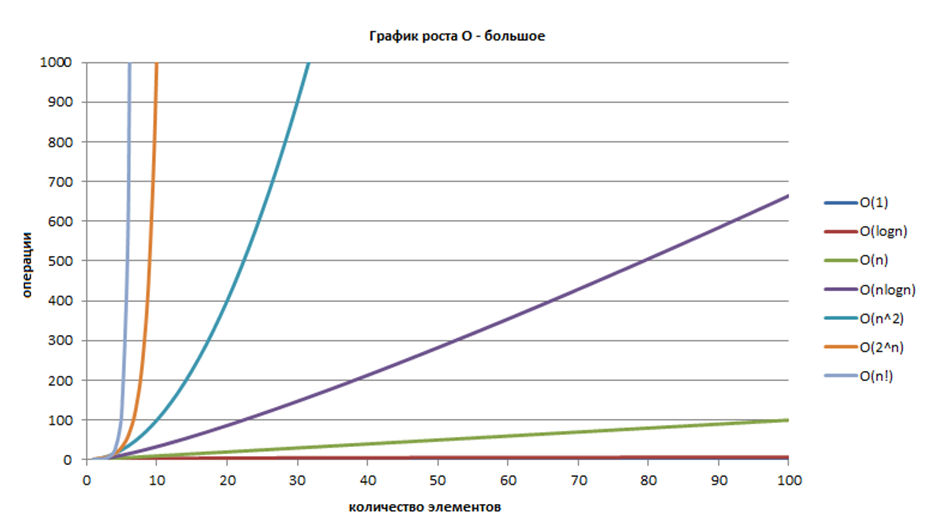
この写真はこの記事からのものです。

また、動的プログラミングの使用例を検討し、アルゴリズムの開発と理解のためのツールを拡張しました。 これらの原則は、他の問題を調査するときに役立ちます。

理解を深めるために、これらの問題を通常の言語で自分でエンコードすることをお勧めします。 また、コメントにあなたの決定へのリンクを投稿することも素晴らしいでしょう。

また、最大のサブシーケンス自体を導出するために、O（n * log n）の最後のアルゴリズムを最終化する方法について考えることを提案します。 コメントに答えを書いてください。

ご清聴ありがとうございました、すぐに会いましょう！

参照：
Stackoverflow.comに関する質問
C ++およびJavaの実装例
説明されたビデオ