インタビューで出会った2つの幾何学的なパズルとそれらが住んでいる場所

アイソメ図形は、同じ面積を持つ図形です。 直線が中心を通る場合、円は半分に分割されることに注意してください。 長方形は、対角線の交点の中心を通る線で半分に分割されます。 まあ、キャプテンは、長方形の図形の中心とカットされた丸い部分を直線で結ぶと、図形の等しい部分が得られることも教えてくれます。 長方形と円の中心が一致しない場合、このような直線は1本です。 図形の中心が一致する場合、線の数は無限になります。 できた

もう一度条件を注意深く読んだ場合、4つのポイントが同じ平面上にないことに注意してください。 この情報は、目的の平面から等距離の条件を満たす点の可能な位置の数を減らします。

1）3つのポイントが問題の平面の片側にあり、4番目がもう一方にあります。
2）平面の両側に2つのポイントがあります。

最初のケースを考えると、3つのポイントを1つの直線に配置する可能性はすぐに除外されます。これは、これらの3つのポイントと4番目のポイントを通る平面を描くことができるためです。 したがって、目的の平面は、選択した3つのポイント（A、B、Cなど）から等距離でなければなりません。つまり、これらのポイントを通る平面ABCに平行でなければなりません。 ただし、目的の平面は点Dから等距離になければならないため、点Dから平面ABCに落とした、垂直DPの中央を通る平面ABCに平行な平面を描きます。



4つのポイントに関して、これらのポイントから等距離にある4つの望ましい平面を取得し、1つのポイントのみがそれらの片側に位置し、残りの3つが他の側にあるようにします。

2番目のケースを検討します。

点AとBが目的の平面の片側にあり、点CとDがもう一方の面にあるとします。 目的の平面は点AおよびBから等距離にあるため、線ABに平行でなければなりません。 また、この平面は点CおよびDから等距離にあるため、直線CDに平行でなければなりません。 点A、B、C、およびDは1つの平面に存在せず、線ABとCDは交差しています。




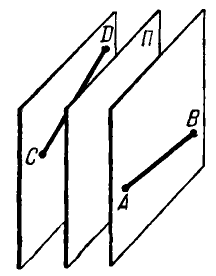
これらの交差した直線を平面に平行に描きます。 目的の平面が問題のポイントから等距離にあるためには、交差する直線を介して構築された平面に平行であり、これらの平面のちょうど中間を通過する必要があります。 また、検討中のこのような各ケースでは、目的のプレーンが一意になります。


したがって、4つのポイントのデータから等距離にある3つの平面があり、一方には4つのポイントのうちの2つがあり、他方には他の2つ（ABとCD、ACとBD、ADとBC）があります。

したがって、これらの4つのポイントから等距離にあるプレーンの合計数は7です（最初のケースを考慮した場合は4つ、2番目のケースを考慮した場合は3つ）。 2番目の問題は解決されました。