オフトップ
記事のタイトルが適合しませんでした-これらの結果は、 Graph500の評価によるとそのように見なされます。 また、調査中に実験的な打ち上げを行うために提供されたリソースについて、IBMとRSCに感謝します。
はじめに
幅優先検索(BFS)は、主要なグラフトラバーサルアルゴリズムの1つであり、多くの高レベルグラフ分析アルゴリズムの基本です。 グラフ全体の検索は、不規則なメモリアクセスと不規則なデータ依存性を持つタスクであり、既存のすべてのアーキテクチャへの並列化を大幅に複雑にします。 この記事では、さまざまなアーキテクチャ(Intel x86、IBM Power8 +、Intel KNL、NVidia GPU)で大規模なグラフを処理するための幅優先検索アルゴリズム( Graph500評価のメインテスト)の実装について説明します。 共有メモリでのアルゴリズムの実装の特徴、およびグラフ変換により、すべてのシングルノードレーティングシステムGraph500およびGreenGraph500でこのアルゴリズムで記録的なパフォーマンスとエネルギー効率の指標を達成できるようになります 。
最近、グラフィックアクセラレータ(GPU)は、非グラフィカルコンピューティングでますます重要な役割を果たしています。 それらの使用の必要性は、それらの比較的高い生産性と低コストによるものです。 ご存知のように、GPUおよび中央処理装置(CPU)では、並列処理が何らかの方法で簡単に区別される構造的な通常のグリッドで問題が十分に解決されます。 ただし、大容量を必要とし、非構造化グリッドまたはデータを使用するタスクがあります。 そのようなタスクの例は次のとおりです。単一の最短ソースパス問題( SSSP )-重み付きグラフ内の特定の頂点から他のすべてへの最短パスを見つけるタスク、幅優先検索タスク(BFS [1])-無向グラフの幅優先探索タスク、最小スパニングツリー(例えば、MST、 外部および私の実装)-強く関連するコンポーネントなどを見つけるタスク。
これらのタスクは、多くのグラフアルゴリズムの基本です。 現在、BFSおよびSSSPアルゴリズムは、Graph500およびGreenGraph500の評価でコンピューターをランク付けするために使用されています。 BFS(幅優先検索または幅優先検索)アルゴリズムは、最も重要なグラフ分析アルゴリズムの1つです。 特定のグラフ内のノード間の接続のプロパティを取得するために使用されます。 基本的に、BFSはリンクとして使用されます。たとえば、接続コンポーネントの検索[2]、最大フローの検索[3]、中心コンポーネントの検索(中間中心性)[4、5]、クラスタリング[6]などのアルゴリズムで使用されます。
BFSアルゴリズムの線形計算の複雑さはO(n + m)です。ここで、nは頂点の数、mはグラフのエッジの数です。 この計算の複雑さは、順次実装に最適です。 ただし、逐次実装(たとえば、 ダイクストラアルゴリズムを使用 )にはデータの依存関係があるため、並列化を妨げるため、この計算の複雑さの評価は並列実装には適用されません。 また、このアルゴリズムのパフォーマンスは、特定のアーキテクチャのメモリパフォーマンスによって制限されます。 したがって、すべてのレベルのメモリを使用して作業を改善することを目的とした最適化が最も重要です。
既存のソリューションとGraph500レーティングの概要
Graph500およびGreenGraph500
Graph500レーティングは、 Top500レーティングの代替として作成されました。 この評価は、後者とは異なり、不規則なメモリアクセスを使用するアプリケーションでコンピューターをランク付けするために使用されます。 Graph500レーティングのテスト対象アプリケーションでは、メモリと通信の帯域幅が最も重要な役割を果たします。 GreenGraph500評価はGreen500評価の代替であり、 Graph500に加えて使用されます。
Graph500はメトリック-グラフの処理されたエッジの1秒あたりの数(TEPS-走査されたエッジ/秒)を使用し、GreenGraph500はメトリック-グラフの処理されたエッジの1秒あたりのワット数を使用します。 したがって、最初の評価ではコンピューターの速度が計算速度でランク付けされ、2番目の評価ではエネルギー効率がランク付けされます。 これらの評価は6か月ごとに更新されます。
既存のソリューション
幅優先の検索アルゴリズムは、50年以上前に作られました。 また、さまざまなデバイスでの効果的な並列実装のための研究が進行中です。 このアルゴリズムは、コンピューターのメモリおよび通信環境での作業がどれだけうまく構成されているかを示します。 x86システム[7-11]およびGPU [12-13]でこのアルゴリズムを並列化する作業は数多くあります。 また、実装されたアルゴリズムの実装の詳細な結果は、Green500およびGreenGraph500の評価で確認できます。 残念ながら、多くの効果的な実装のアルゴリズムは、外国の情報源では公開されていません。
Graph500評価で単一ノードシステムのみを選択した場合、次の表に示されているいくつかのデータが取得されます。 このペーパーで説明する結果は太字でマークされています。 テーブルには、2 25を超える頂点の数を持つグラフが含まれていました。 得られたデータから、現時点では、この記事で提案したよりも1つのノードのみを使用した効率的な実装はないことが明らかです。 より詳細な分析については、「結果の分析」セクションを参照してください。
| 役職 | システム | サイズ2 N | Gteps | ワット |
|---|
| 50 | GPU NVidia Tesla P100 | 26 | 204 | 175 |
| 67 | GPU NVidia GTXタイタン | 25 | 114 | 212 |
| 76 | 4 x Intel Xeon E7-4890 v2 | 32 | 55.9 | 1153 |
| 86 | GPU NVidia Tesla P100 | 30 | 41.7 | 235 |
| 103 | GPU NVidia GTXタイタン | 25 | 17.2 | 233.8 |
| 104 | Intel Xeon E5 2699 v3 | 30 | 16.3 | 145 |
| 106 | 4基のAMD Radeon R9 Nano GPU | 25 | 15.8 | |
| 112 | IBM POWER8 + | 30 | 13.2 | 200 |
グラフ保存形式
非指向RMATグラフは、BFSアルゴリズムのパフォーマンスを評価するために使用されます。 RMATグラフは、ソーシャルネットワーク、インターネットからの実際のグラフをうまくモデル化しています。 この場合、頂点16の平均連結度を持つRMATグラフを検討し、頂点の数は2のべき乗です。 このようなRMATグラフには、1つの大きな接続コンポーネントと、多数の小さな接続コンポーネントまたはぶら下がり頂点があります。 コンポーネントが強力に接続されているため、グラフをキャッシュメモリに収まるサブグラフに分割することはできません。
グラフを作成するには、Graph500評価の開発者によって提供されるジェネレーターが使用されます。 このジェネレーターは、RMAT形式で無向グラフを作成し、出力はグラフエッジのセットとして表示されます。 このような形式は、各頂点の集約情報、つまりどの頂点が与えられた頂点の近傍であるかが必要なため、グラフアルゴリズムの効率的な並列実装にはあまり便利ではありません。 このプレゼンテーションに便利な形式は、CSR(Compressed Sparse Rows)と呼ばれます。
この形式は、疎行列とグラフの保存に広く使用されています。 N個の頂点とM個のエッジを持つ無向グラフの場合、X(隣接する頂点へのポインターの配列)とA(隣接する頂点のリストの配列)の2つの配列が必要です。 配列XのサイズはN + 1で、配列Aは2 * Mです。これは、任意の頂点ペアの無向グラフでは、直接アークと逆アークを保存する必要があるためです。 配列Xは、配列Aにある隣接リストの先頭と末尾を格納します。つまり、頂点Jの隣接リスト全体は、インデックスX [J]からX [J + 1]までの配列Aにあります。 説明のために、下の図は、左側に隣接行列を使用して記述された4つの頂点のグラフと、右側にCSR形式で示されています。
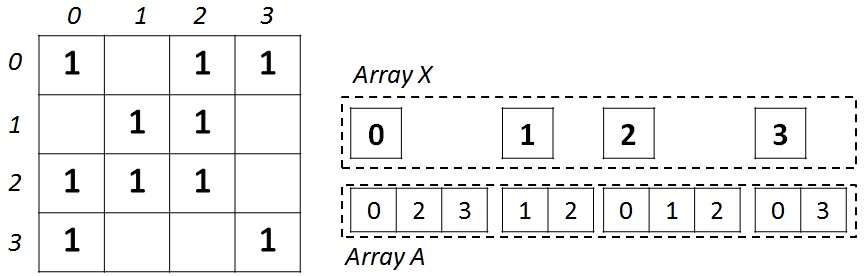
グラフをCSR形式に変換した後、コンピューティングデバイスのキャッシュとメモリの効率を向上させるには、入力グラフでさらに作業を行う必要があります。 以下に説明する変換を実行した後、グラフは同じCSR形式のままですが、実行された変換に関連するいくつかのプロパティを取得します。
導入された変換により、CSR形式のほとんどのグラフトラバーサルアルゴリズムに最適な形式でグラフを構築できます。 グラフに新しい頂点を追加しても、すべての変換が新たに実行されるわけではありません。ルールに従って頂点を追加すれば、頂点の一般的な順序に違反することはありません。
頂点のリストをローカルで並べ替える
各頂点について、隣接リストを増やしてソートします。 並べ替えキーとして、並べ替えられた各頂点の近傍の数を使用します。 この並べ替えを実行した後、各頂点で近傍のリストをクロールすることにより、最初に最も重い頂点(多数の近傍を持つ頂点)を処理します。 このソートは、頂点ごとに独立して並行して実行できます。 このソートを実行した後、メモリ内のグラフの頂点の数は変わりません。
頂点リストのグローバルソート
グラフのすべての頂点のリストについては、昇順で並べ替えます。 キーとして、各頂点の近傍数を使用します。 ローカルソートとは異なり、リスト内の頂点の位置が変わるため、このソートでは結果の頂点の番号を付け直す必要があります。 ソート手順は複雑度O(N * log(N))であり、順番に実行されますが、頂点の番号を変更する手順は並行して実行でき、メモリのあるセクションを別のセクションにコピーするのにかかった時間と速度が同等です。
グラフのすべての頂点の番号を付け直す
最も接続された頂点が最も近い番号を持つように、グラフの頂点に番号を付けます。 この手順は次のように構成されています。 最初に、番号を付け直すためにリストから最初の頂点が取得されます。 番号0を取得します。次に、問題の頂点を持つすべての隣接する頂点が番号を付け直すためにキューに追加されます。 再番号付けリストの次の頂点は、番号1を取得します。 この操作の結果、接続された各コンポーネントで、最大頂点数と最小頂点数の差が最小になり、コンピューティングデバイスの小さなキャッシュサイズを最大限に活用できます。
アルゴリズムの実装
無向グラフの幅優先探索アルゴリズムは、次のように構成されています。 入力では、グラフ内の未定義の頂点の初期頂点(検索のルート頂点)が提供されます。 アルゴリズムは、ルート頂点から開始して、グラフ内の各頂点が位置するレベルを決定する必要があります。 レベルは、ルート頂点からルートとは異なる頂点に到達するために克服しなければならないエッジの最小数を指します。 また、ルートを除く各頂点について、親の頂点を決定する必要があります。 1つの頂点に複数の親頂点を含めることができるため、それらのいずれかが回答として受け入れられます。
幅優先検索アルゴリズムにはいくつかの実装があります。 最も効果的な実装は、レベル同期を使用した反復グラフトラバーサルです。 各ステップは、レベルJの情報がレベルJ + 1に転送されるアルゴリズムの反復です。 シーケンシャルアルゴリズムの擬似コードをここに示します 。
並列実装は、この記事の著者によって提案されたトップダウン(TD)およびボトムアップ(BU)プロシージャで構成されるハイブリッドアルゴリズムに基づいています[11]。 このアルゴリズムの本質は次のとおりです。 TDプロシージャを使用すると、グラフの頂点を直接の順序で移動できます。つまり、頂点を並べ替え、関係を考慮します。 親子として。 2番目の手順BUを使用すると、頂点を逆の順序でバイパスできます。つまり、頂点を並べ替えて、関係を考慮します。 親の子孫として。
TD-BUハイブリッドアルゴリズムの順次実装を検討してください。その擬似コードを以下に示します。 頂点グラフを処理するには、現在のレベルの頂点のセット-Q curr 、および次のレベルの頂点のセット-Q nextを含む2つの追加のキュー配列を作成する必要があります。 キュー内の頂点の存在をより高速にチェックするには、訪問した頂点の配列を入力する必要があります。 しかし、アルゴリズムの作業の結果として、各頂点がどのレベルにあるかについての情報を取得する必要があるため、この配列は、訪問されマークされた頂点のインジケータとしても使用できます。
シリアルBFSハイブリッドアルゴリズム:
void bfs_hybrid(G, N, M, Vstart) { Levels <- (-1); Parents <- (N + 1); Qcurr+=Vstart; CountQ=lvl=1; while (CountQ) { CountQ = 0; vis = 0; inLvl = 0; if (state == TD) foreach Vi in Qcurr foreach Vk in G.Edges(Vi) inLvl++; if (Levels[Vk] == -1) Qnext += Vk; Levels[Vk] = lvl; Parents[Vk] = Vi; vis++; else if (state == BU) foreach Vi in G if (Levels[Vi] == -1) foreach Vk in G.Edges(Vi) inLvl++; if (Levels[Vk] == lvl - 1) Qnext += Vi; Levels[Vi] = lvl; Parents[Vi] = Vk; vis++; break; change_state(Qcurr, Qnext, vis, inLvl, G); Qcurr <- Qnext; CountQ = Qnext.size(); } }
アルゴリズムのメインループは、Q currキュー内の各頂点の順次処理で構成されます。 Q currキューに頂点が残っていない場合、アルゴリズムは停止し、応答が受信されます。
キューには頂点が1つしか含まれていないため、アルゴリズムの最初の段階でTDプロシージャが機能し始めます。 TDプロシージャでは、キューQ currからの各頂点V iについて、この頂点V kの隣接リストを調べ、まだ訪問済みとしてマークされていないものをキューQに追加します。 また、そのような頂点V kはすべて、現在のレベルの番号と親頂点V iを受け取ります。 Q currキューからすべての頂点を表示した後、次の状態を選択する手順が開始されます。これは、次の反復のためにTD手順に残るか、手順をBUに変更することができます。
BUプロシージャでは、Q currキューからではなく、まだマークされていない頂点を調べます。 この情報はレベルの配列に含まれています。 そのような頂点V iがまだラベル付けされていない場合、そのすべての近傍V kを通過し、V iの親であるこれらの頂点が前のレベルにある場合、頂点V iはキューQ nextに入ります。 TDプロシージャとは異なり、このプロシージャでは、親頂点を見つけるだけで十分なので、隣接する頂点V kの表示を中断できます。
TDプロシージャのみで検索する場合、アルゴリズムの最後の反復では、処理する必要のある頂点のリストが非常に大きくなり、マークされていない頂点がかなり多くなります。 したがって、プロシージャは不要なアクションと不要なメモリアクセスを実行します。 BUプロシージャのみで検索する場合、アルゴリズムの最初の反復で未割り当ての頂点が多くなり、TDプロシージャと同様に、追加のアクションと追加のメモリアクセスが実行されます。
最初の手順はBFSアルゴリズムの最初の反復で有効であり、2番目の手順は最後に有効であることがわかります。 両方の手順を使用すると、最大の効果が得られることは明らかです。 あるプロシージャから別のプロシージャに切り替える必要がある時期を自動的に判断するために、この記事の著者によって提案されたアルゴリズム(change_stateプロシージャ)を使用します[11]。 このアルゴリズムは、2つの隣接する反復で処理された頂点の数に関する情報に基づいて、トラバースの動作の性質を理解しようとします。 このアルゴリズムは、処理されたグラフに応じて、1つの手順から別の手順への切り替えを構成できる2つの係数を導入します。
状態遷移手順は、TDをBUに変換するだけでなく、BUをTDに戻すこともできます。 状態の最後の変更は、表示する必要がある頂点の数が非常に少ない場合に役立ちます。 このために、マーク付きピークとマークなしピークの立ち上がりフロントと減衰フロントの概念が導入されています。 以下に示す次の擬似コードは、調整されたアルファおよびベータ係数に応じて、グラフトラバーサルの特定の反復で得られた特性に応じて状態の変更を実行します。 この関数は、 要因に応じて任意の入力グラフで構成できます(要因とは、グラフの頂点の平均接続性を指します)。
状態変更機能:
state change_state(Qcurr, Qnext, vis, inLvl, G) { new_state = old_state; factor = GM / GN / 2; if(Qcurr.size() < Qnext.size())
上記のBFSアルゴリズムのハイブリッド実装の概念は、このようなシステムのCPUとGPUの両方の並列実装に使用されました。 ただし、後で説明するいくつかの違いがあります。
共有メモリ上のCPUでの並列実装
CPUシステム(Power 8 +、Intel KNL、およびIntel x86)の並列実装は、 OpenMPを使用して実行されました。 同じコードが実行に使用されましたが、各プラットフォームにはOpenMPディレクティブの独自の設定がありました。たとえば、スレッド間での負荷分散の異なるモード(スケジュール)が設定されました。 OpenMPを使用してCPUに実装するために、別のグラフ変換を実行できます。つまり、近隣の頂点のリストを圧縮します。
圧縮は、配列Aから各要素の重要でないゼロビットを削除することで構成され、この変換は各範囲[X i 、X i + 1 )に対して個別に行われます。 配列Aの要素は圧縮され、この圧縮により、2 30頂点と2 34エッジのオーダーの大きなグラフの場合、グラフの保存に使用されるメモリ量が約30%削減されます。 小さいグラフの場合、グラフの最大頂点数を占めるビット数が減少するため、このような変換による節約は比例して増加します。
このようなグラフ変換は、頂点処理にいくつかの制限を課します。 まず、すべての隣接する頂点は圧縮され、特定の方法で要素のシーケンスにエンコードされているため、順番に処理する必要があります。 第二に、圧縮要素を解凍するために追加の手順を実行する必要があります。 この手順は簡単ではなく、Power8 + CPUの場合、効果を得ることができませんでした。 その理由は、コンパイラーの最適化が不十分であるか、Intelとは異なるハードウェアである可能性があります。
アルゴリズムの1つの反復を並行して実行するには、OpenMPストリームごとに独自のQ th_nextキューを作成する必要があります。 そして、すべてのループを完了した後、受信したキューをマージします。 また、縮約依存があるすべての変数をローカライズする必要があります。 最適化として、Q currキュー内の頂点の数が所定のしきい値(たとえば、300未満)未満の場合、TDプロシージャはシーケンシャルモードで実行されます。 さまざまなサイズのグラフの場合、およびアーキテクチャにも依存するため、このしきい値にはさまざまな値を設定できます。 TDプロシージャーの場合はループ(QcurrのForeach Vi)、BUプロシージャーの場合は(QcurのVi Foreach)ループの前に並列ディレクティブが配置されました。
GPU並列実装
GPUの並列実装は、 CUDAテクノロジーを使用して実行されました。 特定のプロシージャの実行中にデータにアクセスするためのアルゴリズムが大幅に異なるため、GPUを使用する場合、TDおよびBUプロシージャの実装は大幅に異なります。
TDプロシージャは、 CUDA動的同時実行性を使用して実装されました。 この機能により、負荷分散に関連するいくつかの作業をGPU機器に転送できます。 キューQ currからの各頂点V iには、以前は未知の数のネイバーに対して完全に異なるものを含めることができます。 このため、CUDAでは固定サイズのスレッドのブロックを使用できるため、一連のスレッドでサイクル全体を直接表示すると、強い負荷の不均衡が発生します。
説明されている問題は、動的並行性を使用することで解決されます。 最初に、マスタースレッドが起動されます。 Q currキューにある頂点と同じ数のスレッドがあります。 次に、各マスタースレッドは、頂点V iに隣接するスレッドと同じ数の追加のスレッドを実行します。 したがって、使用されるスレッドの数は、入力データに応じて、プログラムの実行中にダイナミクスで形成されます。
この手順は、動的並列処理を使用する必要があるため、GPUでの実行には不便です。 マスタースレッドから作成する必要があるスレッドの総数が多いと、オーバーヘッドが大きくなります。 したがって、BUプロシージャへの切り替えは、CPUよりも早く実行されます。
追加のデータ変換を行う場合、BUプロシージャはGPUでの実行に適しています。 この手順は、グラフの連続するすべての頂点で通過が実行されるという点で、TD手順とは大きく異なります。 したがって、組織化されたサイクルにより、メモリへの適切なアクセスのためのデータ準備を実行できます。
変換は次のとおりです。 1つのワープの隣接するスレッドが命令を同期的かつ並列に実行することが知られています。 また、効果的なメモリアクセスでは、ワープ内の隣接スレッドがメモリ内の隣接セルにアクセスする必要があります。 たとえば、ワープのスレッド数を2に設定します。各スレッドがループの1つの頂点に関連付けられている場合(GのViごと)、ループ内のネイバーの処理中(GのVkごと。エッジ(Vi))、各スレッドはメモリ領域に移動します、隣接するスレッドがメモリ内の間隔の広いセルを処理するため、パフォーマンスに悪影響を及ぼします。 状況を修正するには、配列Aの要素を混合して、V 0とV 1の最初の2つの隣接要素に最適な方法でアクセスします。隣接要素はメモリ内の隣接セルに配置されます。 さらに、2番目、3番目なども同様にメモリ内にあります。 要素。
この整列ルールは、ワープスレッドのグループ(32スレッド)に適用されます。隣接するスレッドが混合されています。最初の32個の要素が最初に配置され、次に2番目の32個の要素が配置されます。 グラフは近隣の数の降順で並べ替えられているため、隣接する頂点のグループは、近隣の頂点の数がかなり近くなります。
BUプロシージャの操作中、内部ループに早期終了があるため、グラフ全体でこの方法で要素を混在させることはできません。 上記のグローバルおよびローカルの頂点ソートにより、このサイクルをかなり早く終了できます。 したがって、グラフのすべての頂点の40%のみが混合されます。 この変換では、混合グラフを保存するために追加のメモリが必要になりますが、パフォーマンスが大幅に向上します。 以下は、メモリ内の要素の混合配置を使用したBUプロシージャのカーネル擬似コードです。
BU手順の並列カーネル:
__global__ void bu_align( ... ) { idx = blockDim.x * blockIdx.x + threadIdx.x; countQNext = 0; inlvl = 0; for(i = idx; i < N; i += stride) if (levels[i] == 0) start_k = rowsIndices[i]; end_k = rowsIndices[i + N]; for(k = start_k; k < start_k + 32 * end_k; k += 32) inlvl++; vertex_id_t endk = endV[k]; if (levels[endk] == lvl - 1) parents[i] = endk; levels_out[i] = lvl; countQNext++; break; atomicAdd(red_qnext, countQNext); atomicAdd(red_lvl, inlvl); }
結果の分析
テストされたプログラムは、Intel Xeon Phi(Xeon KNL 7250)、Intel x86(Xeon E5 2699 v3)、IBM Power8 +(Power 8+ s822lc)、およびNVidia Tesla P100 GPUの4つの異なるプラットフォームですぐに実行されました。 対象のこれらのデバイスの特性を比較します
下の表。
次のコンパイラが使用されました。 Intel Xeon E5の場合-gcc 5.3、Intel KNLの場合-icc v17、IBMの場合-gccのPowerアーキテクチャー、NVidiaの場合-CUDA 9.0。
| 仕入先 | コア/スレッド | 周波数、GHz | RAM、GB / s | マックス TDP、W | Trans。、Billion |
|---|
| Xeon KNL 7250 | 68/272 | 1.4 | 115/400 | 215 | 〜8 |
| Xeon E5 2699 v3 | 18/36 | 2.3 | 68 | 145 | 〜5.69 |
| Power 8+ s822lc | 10/80 | 3.5 | 205 | 270 | 〜6 |
| テスラP100 | 56/3584 | 1.4 | 40/700 | 300 | 〜15.3 |
最近、メーカーはメモリ帯域幅についてますます考えています。 この結果、RAMへの低速アクセスの問題に対するさまざまな解決策が現れます。 検討中のプラットフォームのうち、2つには2レベルのRAM構造があります。
それらの最初の-インテルKNLは、アクセス速度が約400 GB / sのチップ上の高速メモリと、アクセス速度が115 GB / s以下のより遅いおなじみのDDR4を含んでいます。 高速メモリのサイズはかなり小さく、16GBしかありませんが、通常のメモリは最大384GBです。 テストしたサーバーに96 GBのメモリがインストールされました。 2番目のハイブリッドソリューションプラットフォームは、Power + NVidia Teslaです。 このソリューションは新しいNVlinkテクノロジーに基づいており、通常のメモリへのアクセスは40 GB /秒の速度で、高速メモリへのアクセスは700 GB /秒の速度で実行されます。 高速メモリの量は、Intel KNL-16GBと同じです。
これらのソリューションは、組織の点で似ています-サイズの小さい高速メモリとサイズの大きい低速メモリがあります。 大きなグラフを処理するときに2レベルのメモリを使用するシナリオは明らかです。高速メモリは結果と中間配列を格納するために使用され、そのサイズは入力データに比べて非常に小さく、元のグラフは低速メモリから読み取られます。
実装の観点から、ユーザーは次のツールを使用できます。 Intel KNLの場合、通常のmallocの代わりに他のメモリ割り当て関数hbm_mallocを使用するだけで十分です。 プログラムがmalloc演算子を使用した場合、この機能を使用するには、1つの定義を宣言するだけで十分です。 NVidia Teslaの場合、他のメモリ割り当て関数も使用する必要があります-cudaMallocの代わりにcudaMallocHostを使用します。 これらのコードの修正は十分であり、プログラムの計算部分の修正を必要としません。
実験は、2 25 (4 GB)から2 30 (128 GB)で終わるさまざまなサイズのグラフに対して行われました。 Graph500の評価では、平均的な接続の度合いとグラフの種類はグラフジェネレーターから取得しました。 このジェネレーターは、平均連結度16および係数A = 0.57、B = 0.19、C = 0.19のクロネッカーグラフを作成します。
このタイプのグラフは、評価表のすべての参加者が使用するため、参加者間で実装を正しく比較できます。 パフォーマンス値は、Graph500テーブルのTEPSメトリックとGreenGraph500テーブルのTEPS / wに従って計算されます。 この特性を計算するために、異なる開始頂点からのBFSアルゴリズムの64回の開始が実行され、平均値が取得されます。 アルゴリズムの消費量を計算するために、メモリ消費量を考慮に入れて、アルゴリズム操作時の現在のシステム消費量が取得されます。
次の表は、テストされたすべてのグラフのGTEPSでの結果のパフォーマンスを示しています。 表には2つの値が示されています。各グラフで達成されたパフォーマンスの最小値/最大値です。 また、Intel KNLを使用する場合、アルゴリズムの結果はDDR4メモリのみを使用して取得されました。 残念ながら、すべてのデータ圧縮アルゴリズムを使用する場合でも、提供されたサーバー上のIntel KNLで2 30の頂点を持つグラフを実行することはできませんでした。 しかし、Intelプロセッサーの安定性とIntelコンパイラーのテクノロジーを考えると、グラフサイズが大きくなってもパフォーマンスは変わらないと想定できます(Intel Xeon E5で見られるように)。
GTEPSでの結果のパフォーマンス:
| カウント: | 2 25 | 2 26 | 2 27 | 2 28 | 2 29 | 2 30 |
|---|
| KNL 7250 | 10.7 / 30.6 | 12.9 / 41 | 8.4 / 43.3 | 4.6 / 40.2 | 6.2 / 42.6 | N / a |
| KNL 7250 DDR4 | 6.7 / 25.2 | 4.3 / 27 | 4.9 / 28.4 | 5.7 / 31.6 | 10.8 / 38.8 | N / a |
| E5 2699 v3 | 11 / 16.5 | 11.8 / 17.3 | 12.7 / 18.5 | 13.1 / 18.3 | 12.1 / 18.0 | 12.4 / 21.1 |
| P8 + s822lc | 8.8 / 22.5 | 9.02 / 23.3 | 7.98 / 23.4 | 10.4 / 23.7 | 10.1 / 24.6 | 7.59 / 14.8 |
| テスラP100 | 41/282 | 99/333 | 34/324 | 50/274 | 7.2 / 61 | 6.5 / 52 |
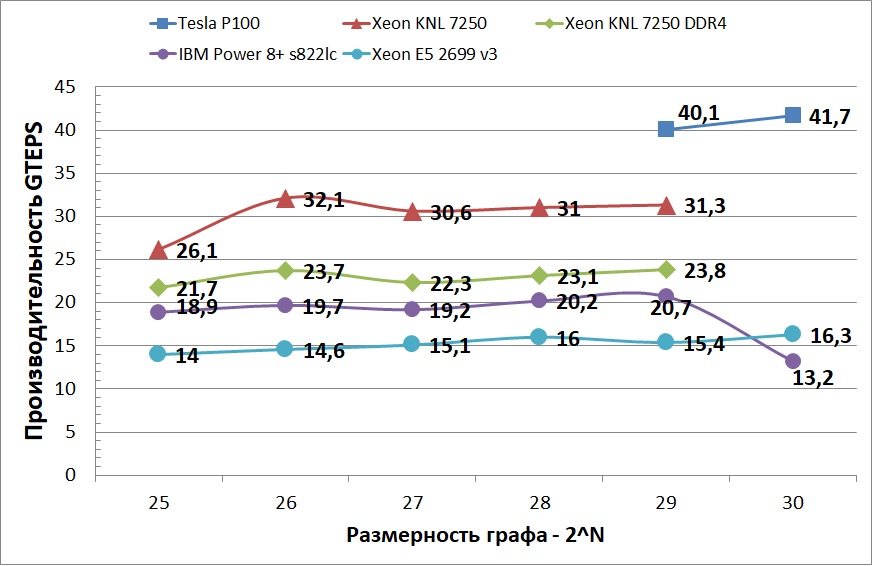
以下のグラフは、テストされたプラットフォームの平均パフォーマンスを示しています。 64 GBから128 GBのグラフに切り替えると、Power 8+の安定性があまり良くないことがわかります。 これはおそらく、2つの類似したプロセッサから2つのソケットを使用し、各プロセッサに128 GBのメモリがあったためです。 また、より大きなグラフを処理する場合、データの一部は、ソケットに属さないメモリに配置されました。 また、最速のCPUデバイスとGPUの差は約10倍であるため、このグラフでは、より小さいグラフでのTesla P100のパフォーマンスは表示されません。 グラフが非常に大きくなりキャッシュに収まらず、NVlinkを介してグラフにアクセスすると、この加速は急激に低下します。 しかし、この制限にもかかわらず、GPUのパフォーマンスは依然としてすべてのCPUデバイスを上回っています。 この動作は、CUDAを使用するとコンピューティングとメモリアクセスをより適切に制御でき、GPUの並列コンピューティングへの適応性が向上するという事実によって説明されます。
以下の表は、テストされたすべてのグラフのGTEPS / wでの結果のパフォーマンスを示しています。 表には、各グラフの平均消費電力と達成された平均パフォーマンスが示されています。 NVidia Tesla P100で列2 28から列2 29に切り替えるときのパフォーマンスとエネルギー効率の急激な低下は、最も頻繁にアクセスされるグラフの整列部分を配置するのに十分な高速メモリがないという事実によって説明されます。 より多くのメモリ(32 GBなど)を使用し、NVlink 2.0 CPUとの通信チャネルを増やすと、大きなグラフの処理効率を大幅に高めることができます。
結果として生じるエネルギー効率はMTEPS / wで表されます。
| グラフサイズ | 2 25 | 2 26 | 2 27 | 2 28 | 2 29 | 2 30 |
|---|
| KNL 7250 | 121.4 | 149.3 | 142.33 | 136.56 | 130.96 | N / a |
| E5 2699 v3 | 95.56 | 98.65 | 100 | 101.9 | 91.12 | 84.46 |
| P8 + s822lc | 93.8 | 97.04 | 93.2 | 95.28 | 92.41 | 53.23 |
| テスラP100 | 1228.57 | 1165.71 | 1235.96 | 1016.57 | 195.61 | 177.45 |
そして最後に
行われた作業の結果として、2つの並列BFSアルゴリズムが、同様のシステムのCPUとGPUに実装されました。 IBM Power8 +、Intel x86、Intel Xeon Phi(KNL)、NVidia Tesla P100などのさまざまなプラットフォームに実装されたアルゴリズムのパフォーマンスとエネルギー効率の調査が行われました。 これらのプラットフォームには、さまざまなアーキテクチャ機能があります。 それにもかかわらず、最初の3つは構造が非常に似ています。 これにより、OpenMPアプリケーションはこれらのプラットフォームで大きな変更なしに起動できます。 それどころか、GPUアーキテクチャは同様のプラットフォームのCPUとは非常に異なり、計算コードを実装するためにCUDAアーキテクチャという異なる概念を使用しています。
Graph500レーティングのジェネレーターの後に取得されたグラフが考慮されました。 2つのデータクラスでの各アーキテクチャのパフォーマンスを調査しました。 最初のクラスには、コンピューターの最速のメモリーに配置されるグラフが含まれます。 2番目のクラスには、全体として高速メモリに配置できない大きなグラフが含まれます。 GreenGraph500メトリックは、エネルギー効率を実証するために使用されました。 ビッグデータクラスのGreenGraph500評価で考慮される最小グラフは、2 30の頂点と2 34のエッジを含み、元の形式で128 GBのメモリを占有します。 2 30 2 34 , , .
Graph500 GreenGraph500 NVidia Tesla P100 ( 220 GTEPS 1235.96 MTEPS/w), ( 41.7 GTEPS 177.45 MTEPS/w). NVLink, IBM Power8+.
NVidia Volta NVlink 2.0, .
, ( =)[1] EF Moore. The shortest path through a maze. In Int. Symp. on Th.
of Switching, pp. 285–292, 1959
[2] Cormen, T., Leiserson, C., Rivest, R.: Introduction to Algorithms. MIT Press,
Cambridge (1990)
[3] Edmonds, J., Karp, RM: Theoretical improvements in algorithmic efficiency for
network flow problems. Journal of the ACM 19(2), 248–264 (1972)
[4] Brandes, U.: A Faster Algorithm for Betweenness Centrality. J. Math. Sociol. 25(2),
163–177 (2001)
[5] Frasca, M., Madduri, K., Raghavan, P.: NUMA-Aware Graph Mining Techniques
for Performance and Energy Efficiency. In: Proc. ACM/IEEE Int. 確認 High Performance
Computing, Networking, Storage and Analysis (SC 2012), pp. 1–11. IEEE
Computer Society (2012)
[6] Girvan, M., Newman, MEJ: Community structure in social and biological networks.
手続き Natl. Acad. Sci. USA 99, 7821–7826 (2002)
[7] DA Bader and K. Madduri. Designing multithreaded algorithms for
breadth-first search and st-connectivity on the Cray MTA-2. In ICPP,
pp. 523–530, 2006.
[8] RE Korf and P. Schultze. Large-scale parallel breadth-first search.
In AAAI, pp. 1380–1385, 2005.
[9] A. Yoo, E. Chow, K. Henderson, W. McLendon, B. Hendrickson, and
U. Catalyurek. A scalable distributed parallel breadth-first search
algorithm on BlueGene/L. In SC '05, p. 25, 2005.
[10] Y. Zhang and EA Hansen. Parallel breadth-first heuristic search on a shared-memory architecture. In AAAI Workshop on Heuristic
Search, Memory-Based Heuristics and Their Applications, 2006.
[11] Yasui Y., Fujisawa K., Sato Y. (2014) Fast and Energy-efficient Breadth-First Search on a Single NUMA System. In: Kunkel JM, Ludwig T., Meuer HW (eds) Supercomputing. ISC 2014. Lecture Notes in Computer Science, vol 8488. Springer, Cham
[12] Hiragushi T., Takahashi D. (2013) Efficient Hybrid Breadth-First Search on GPUs. In: Aversa R., Kołodziej J., Zhang J., Amato F., Fortino G. (eds) Algorithms and Architectures for Parallel Processing. ICA3PP 2013. Lecture Notes in Computer Science, vol 8286. Springer, Cham
[13] Merrill, D., Garland, M., Grimshaw, A.: Scalable GPU graph traversal. In: Proc. 17th ACM SIGPLAN Symposium on Principles and Practice of Parallel Programming (PPoPP 2012), pp. 117–128 (2012)