グループ分極の効果とその数学的モデリング

はじめに

むかしむかし、アメリカの心理学者J.ストーナーは興味深い実験を行いました（当時、人々は非常にひどく免責でm笑される可能性がありました）。 彼は学生のグループを取り、それぞれに（条件付きで）二分した質問を含むアンケートを渡しました。 彼らが答えた後、ストーナーはこれらの問題を一緒に議論するよう彼らを招待しました。 そして議論の後、もう一度同じ質問に答えてください。 彼の偉大な科学的成功にとって、結果は非常に興味深いものでした。

グループでの議論の後、回答は本質的に「危険」になり始めました。 もちろん、「危険」という言葉は、一種のe曲表現であり、イデオロギーの反対者のグループと同じ考えを持つ人々のグループに直面した人々が少し残忍であり、彼らの初期の見解をより積極的に擁護し始めたという事実を隠しています。 この現象は「グループ分極」と呼ばれています。



素朴なことに、科学者たちは（そして今では多くの人たちが）議論がコンセンサスに達するのに役立つと考えています。 いや 二分法の議論は、それが計画されていない場合、コンセンサスに達するのに役立ちません。 議論は、社会が互いに立ち向かうことができない2つのキャンプに分かれるのを助けます。 そして、インターネットの出現とあらゆる機会での無限のインターネット紛争により、このプロセスはさらに野心的になりました 。

しかし、それがどんなに悲しいものであっても、そのようなプロセスの社会的帰結と、このアイデアに対するさまざまな戦闘機の果てしない分極化の叫びは、私をそれほど悩ませません。 しかし、数学の助けを借りてこれをシミュレートする能力に興味があります。

主なアイデア

社会は、各メンバーが-1から1までの数字の形で、特に燃えている問題について自分自身の二分論的な意見を持っているように生成されます。たとえば、赤いズボンや青い服を着ます。 たとえば、図-0.9-に対応する人は赤いズボンが大好きで、0.9-青いズボンが大好きです。 彼のズボンにゼロを持つ男は無関心であり、スカートをはいています。

さらに、各人には一定レベルの保護反応があり、それにより、新しい意見や、何らかの理由で個人的になりたいという願望を受け入れることができなくなります。

繰り返しになると、何らかの社会的行為が発生します。 条件付き-「青いズボンの人が集会に行きました。」 すべてではありませんが、特にイデオロギーです。 集会では、それぞれがランダムな人々と対話します。 彼は、対談者がどれだけ彼と一致しており、人格に転向する傾向がないかに応じて、彼らに同意する場合としない場合があります。
それだけです。

数回繰り返した後、人口全体で異なる色のズボンに対する愛の分布が変化したように見えます。

モデルの説明

「社会」は $$$M$個人。 各個人にはいくつかの特徴があります。

$$$c$-文化的所属。 -1〜1の数値。
$$$d = c + N（0,0.4）$-防衛反応のレベル、と「相関」 $$$c$。 文化に馴染むほど、防御反応は強くなります。 $$$N（0,0.4）$-標準偏差 0.4で0に関して正規分布するランダム変数。
$$$a = U（0,1）$-広告の名声率。 何らかの理由で個人的になりたいという願望。 当然、それが大きければ大きいほど、あなたが異なる見解を持っている人に対する理解が少なくなります。 $$$U（0,1）$-0から1までの均一な分布。

定数：
$$$cs$-文化的文脈を変える基本的なステップ（ズボンの色の愛）。
$$$ds$-保護レベルを変更する基本的なステップ。

反復（公共の社会的行為）：
理想を持つランダムな人々のために $$$c> 0$、乱数と比較することにより、理想の大きさがチェックされます。
もし $$$2c> rand（0,1）$、その人はサンプル全体からランダムに[1：6]人とやり取りします。 そして、不平等があるすべての人にとって。
疑問が生じる場合がある-なぜ $$$2c$しかしではない $$$c$。 配布には、十分に大きなイデオロギーを持つ人々が少なすぎることが判明する可能性があるため、 $$$c$2を掛けます。しかし、一般に、それはすべてから $$$c$依存しないでください。

実際に人々の相互作用：
同じ意見の人なら
当然、問題について口論することはできないため、成功と失敗はチェックされません。 しかし、彼らは互いに同意することで自分自身を主張することができます。 したがって、最初に、彼らが全会一致でどれだけ近いかを見つけます $$$\デルタc = c_1-c_2$そして：

もし $$$p = 1-e ^ {-5（1- \ Delta c）^ 2}> rand（0,1）= r$その後、それぞれ：

$$

$$c = c + sign（c）\ cdot cs \ cdot | p-r |$$

$$

$$d = d + ds \ cdot | p-r |$$

すなわち 彼らは自分の理論をもっと信じており、彼らの理論に関する防御が強化されています。

人々が異なる見解を持っている場合
それから彼ら $$$\デルタc = 0.5（c_1-c_2）$、0.5、ユニットが登らないようにします。 また、同意の確率は次のように考慮されます。

$$

$$p =（1-e ^ {-5（1- \ Delta c）^ 2}）（1-a_1）（1-d_2）$$

ここに $$$a_1$-彼のテキストの相互作用の参加者の性格に行きたいという願望、 $$$d_2$-読者の防御的反応。 当然、パーソナリティへの完全な移行により、理解度が0になり、防御的な反応が強すぎることが保証されます。

通信が成功し、 $$$p$よりランダム $$$r$その後：

$$

$$c_1 = c_1 + sign（c_1）\ cdot cs \ cdot | p-r |、$$

$$

$$c_2 = c_2 + sign（c_1）\ cdot cs \ cdot | p-r |、$$

$$

$$d = d-ds \ cdot | p-r |。$$

知覚者は、視線を参加者に向けます。 両方の防御が落ちます。

通信に失敗した場合、および $$$p$ランダムではない $$$r$その後：

$$

$$c_2 = c_2-sign（c_1）\ cdot cs \ cdot | p-r |、$$

$$

$$d = d + ds \ cdot | p-r |。$$

読む人は参加者から目をそらし、両方の防御力が上がります。
値 $$$c$そして $$$d$-元のサンプルから計算される最大値によって制限されます。

繰り返しますが、保護反応と個人への移行がない場合、同意の可能性のそのような計算に関して疑問が生じる場合があります。 $$$（1-e ^ {-5（1- \ Delta c）^ 2}）$。 しかし、ここではすべてが簡単です $$$（1- \ Delta c）^ 2$-1を超えることのできないメンバー。「5」は経験的に選択するのに適した係数ですが、この場合、プロセスが許容可能な反復回数で収束するように任意に指定されます。

いくつかのモデリングシナリオ

中立社会

1000人 $$$c = N（0,2）$。 150回の繰り返し。


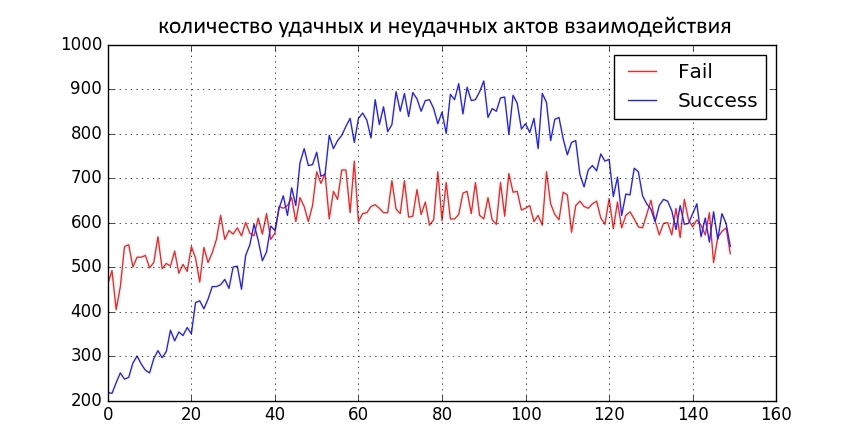上の2つのグラフは、150回の反復にわたるビューの分布がどのように変化したかを示しています。 x軸-ビューの重大度。 y軸上-ビューアーの数（正規化）。 下のグラフは、反復のために反対意見を持つ人々とのやり取りの成功と失敗の回数を示しています。

グラフには何が見えますか？

1. 社会は二分された。
2. 分布の赤い部分は0に「押し込まれ」ましたが、赤のままでした。 すなわち 中程度の赤いズボン愛好家がたくさんいます。
3. 「青」の部分は、中程度のマイナス（赤の部分）になるか、「青」の急進主義にintoいました。
4. 期間中の良好な相互作用の数は増加し、その後減少しました。 これは、青色のものが急進化し、赤色のものが赤のままであるため、予測可能です。
5. 急進化により、より多くの人々がプロモーションに参加し始めました。 その後、分布の青い部分が広がり始め、関与が少なくなりました。

レッドパンツ協会

1000人 $$$c = N（-1,2）$、150回の繰り返し。

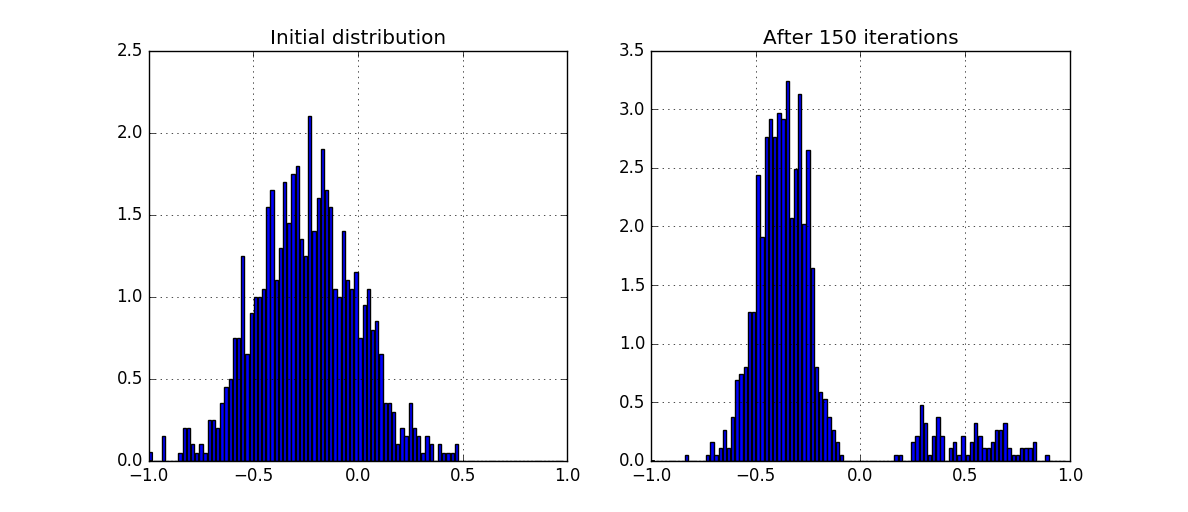
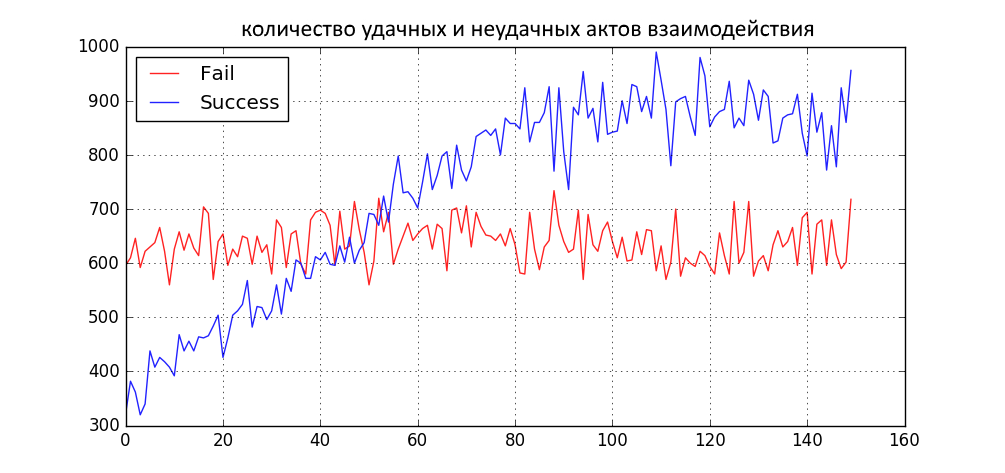
1. 社会は二分された。
2. 「赤い部分」は0に「崩壊」しませんでしたが、このような弱い傾向があります。
3. 青い部分は、ほぼ「均一な」分布に塗りつぶされています。
4. 成功したコミュニケーションとそうでないコミュニケーションの両方の数が増加しました。

二重社会

500人 $$$c = N（-2,2）$、500人 $$$c = N（2,2）$、150個のフラッシュモブ。




状況は最初の状況に近いですが、両方のグループの大きな過激主義によるすぐに大きなレベルの通信障害です。

中立で均質な社会

c = N（0,1）の1000人。 150回の繰り返し。 均一性は、分布が第1の実施形態よりもはるかに狭いという事実にある。 すなわち すべての人々は、自分のズボンの色に最初のナンセンスで非常に近いです。 少しだけ気にしません。 ほんの少し。

1. これは、青いズボンが「勝ち」、赤いズボンが少数派である場合の唯一のオプションです。 これは主に、初期の分布が狭いことに起因します。これは、見解と防御反応に過激主義が少ないため、人々はおそらく呪われていないためです。 パンツの色に無関心な人口は、青いパンツの一般的な採用に移行しています。
2. 肯定的および否定的な相互作用は0になります。同じビューの人々の相互作用では、これらのパラメーターは考慮されないためです。

モデルの制限に関する考慮事項

• 人々が近くのサークルで回転することを考慮していないため、ほとんどの場合、彼らは自分自身と対話します。 しかし。 これは、反対の視点を聞く能力にのみ影響を与えるため、このモデルには相互作用に対してかなり前向きなオプションがあると想定できます。
• サンプルの大部分に直接向かうことができるあらゆる種類のオピニオンリーダーがいることは考慮されていません。
• アクティブな位置は、青いズボンの側面のみです。 彼女だけが「アクション」を保持しています。 ただし、これは設計上の機能であり、バグではありません。
• 天井にはいくつかのオッズがありますが、どこで入手できますか？ 元の実験またはトークショーの投票結果に従ってカスタマイズできます。 見てみましょう。

ミニ出力

このモデルの下では、人々は依然として二分された問題に同意しています。 しかし、彼らが最初に質問について気にしなかった場合にのみ。 これは、人々が質問に興味を持たないか、なじみのないときに「グループ分極」が生じない現象の定性的説明によく適合します。 さらに、モデルから、もし最初に人々が何かについて気にしないなら、彼らが自分の見解として何かを受け入れることははるかに簡単であることがわかります。 問題は、いかに取るに足らないことであり、実際にイデオロギーの深い意見のリーダーによって適用されたことはありません。 人々はすぐに何かを大声で叫び始め、人々がすぐに2つのチームに分かれるようにする必要があります。

記事の著者：Alexander Bespalov、Maxilect、データ分析スペシャリスト