前の章では、機械学習における古典的な判別モデルについて説明し、そのようなモデルの最も単純な例を見てきました。 ここで、より一般的な図を見てみましょう。
人工知能のタスク
人工知能(AI)は、人間と同等以上のレベルの人々が通常解決する問題を解決できるアルゴリズムです。 これには、視覚画像の認識、テキストの理解と分析、メカニズムの制御、論理チェーンの構築があります。 人工知能システムは、こうした問題をすべて一度に効果的に解決できるシステムです。 この問題に対する解決策はまだありませんが、AI問題を解決するための最初のステップと呼ばれるさまざまなアプローチがあります。
20世紀には、ルールベースのアプローチが最も人気がありました。 彼の考えは、世界は、例えば物理学や他の自然科学によって研究されている法則に従うということです。 また、AIで効果的に直接プログラムできない場合でも、十分な数のプログラムされたルールを使用して、コンピューターに基づくAIシステムがこれらのルールに基づいて世界に効果的に存在し、任意の問題を解決できると仮定するのは合理的です。 このアプローチでは、いくつかのイベントの自然確率を考慮していません。 それを考慮するには、ランダムな入力データを条件として、確率的決定を行うためのこのルールのリストに確率モデルを構築する必要があります。
世界を完全に説明するには、非常に多くのルールが必要になるため、それらを手動で設定および保守することはできません。 これにより、現実世界のイベントを十分に観察し、これらの観察から必要なルールを自動的に導出するというアイデアが生まれます。 このアイデアは、いくつかの自然プロセスの実際の確率論と、特定の決定論的プロセスに影響を与える要因が完全にはわからないという事実によって生じる想像上の確率論の両方を即座にサポートします。 観測からのルールの自動導出は、機械学習と呼ばれる数学のセクションによって処理されます。これが現在、AIの最も有望な基盤です。
機械学習AI
前の章では、機械学習の古典的な問題(分類と回帰)と、それらを解決するための古典的な線形手法(ロジスティック回帰と線形回帰)について見てきました。 実際には、非線形モデルは、通常、決定木またはディープ人工ニューラルネットワークに基づいた複雑な問題に使用されます。これらは、高レベルの冗長性を備えた高密度データ(画像、音声、テキスト)の処理よりも優れています。
これらの方法は、観察に基づいてルールを自動的に導出することができ、商用アプリケーションで非常にうまく適用されます。 ただし、AIシステムとして使用するには不十分であるという欠点があります。たとえば、画像内の猫と犬を区別するなど、特定の高度に特殊化された問題を解決するように特別に設計されています。 明らかに、画像を1つの数値に合計するモデルでは、大量のデータが失われます。 画像内の猫を判別するには、猫の本質を理解する必要はありません。この猫の主な兆候を探す方法を学ぶだけで十分です。 画像分類のタスクは、シーンの完全な理解を意味するのではなく、シーン内の特定のオブジェクトの検索のみを意味します。 少なくとも収集およびマークアウトが必要な指数関数的に大量の観測のため、オブジェクトのすべての可能な組み合わせの接続のすべての可能な組み合わせの分類子を決定することはできません。 したがって、特定のタスクが解決される強化を伴う古典的な機械学習問題のアイデアは適切ではありません。 AIの場合、機械学習の問題を定式化するための根本的に異なるアプローチが必要です。
世界を理解する問題の確率論的声明
そのため、一連の観察結果を生成するプロセスを理解するという意味で、観察が必要です。 この問題を確率的言語で再定式化します。 観測を確率変数の実現とする
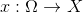
、一連の観測可能なイベントがあります
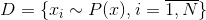
。 その後、イベント全体の多様性の「理解」を、分布を復元するタスクとして定式化できます。

。
この問題を解決するには、いくつかのアプローチがあります。 最も一般的な方法の1つは、潜在変数の導入です。 特定の表現があると仮定します
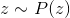
観察

。 このビューは、モデル観察の「理解」について説明します。 たとえば、コンピュータゲームのフレームの場合、そのような理解は、ゲームワールドの関連する状態とカメラの位置になります。 その場合
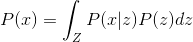
。 修正
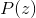
分布のサンプリングが簡単になるように、次のモデルを取得します。
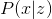
そして

ニューラルネットワークで近似できます。 標準的な深層学習方法でこのモデルを教えることができます

上記の式に従って、その後、確率的推論で使用できます。 そのようなモデルのより正確な定式化は後続の部分で与えられますが、ここでは、そのようなモデルの複雑なバージョンは、複雑な計算不可能な積分の近似を必要とすることに注意する必要があります。 建物

それからサンプルを抽出することは、生成モデリングのタスクと呼ばれます。
別の方法で問題にアプローチできます。 実際、明示的に計算します

、複雑な積分を近似する必要はありません。 1つのアイデアは、モデルが世界を「想像」できる場合、それがどのように機能するかを理解することを意味するということです。 たとえば、人をさまざまなポーズや角度で描くことができる場合、その人体の解剖学と遠近法が一般的にどのように配置されているかがわかります。 モデルによって生成されたオブジェクトを実際のオブジェクトと区別できない場合、モデルは、この現象またはその現象がどのように機能するかを理解し、正直に「理解」することができました。 このアイデアは、暗黙的な生成的モデリングの開発を促します

-有限個の観測値を持ち、それらを一般化し、実際の観測値と区別できない新しい観測値を生成できるモデルの開発。 と仮定する
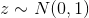
、またはサンプリング用の他の単純な分布。 次に、かなり一般的な条件下で、関数が存在します
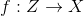
そのような
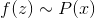
。 この場合、我々は取得しません

明示的にですが、モデルには暗黙的にそれに関する情報が含まれています。 回復の代わりに

復元できる
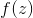
続いてからのサンプル

として入手できます
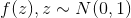
。
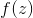
確率的推論に直接使用することはできませんが、第一に、常に必要なわけではありません。第二に、必要な場合は、サンプルを取得するだけのモンテカルロ法を使用できます。 次のパートで学習する生成的敵対ネットワークモデルも、このタイプのメソッドに属します。
主成分分析
単純な生成モデルを見てみましょう。 いくつかの観測可能な量がありましょう
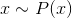
。 たとえば、人の身長やピクセル画像などです。 この値は、隠された(潜在的な)値によって完全に説明されると仮定します。
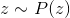
。 私たちの類推では、これは人や物体の重量と画像上での向きです。 今、隠された量のために
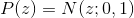
、観測値は通常のノイズに線形に依存します。
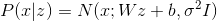
。 このモデルは確率的主成分分析(PPCA)と呼ばれ、実際、古典的
な主成分分析 (PCA)モデルの確率的再定式化です。

潜在変数に線形に依存

ノイズなし。
期待の最大化
期待値最大化(EM)は、潜在変数を持つモデルをトレーニングするためのアルゴリズムです。 詳細は専門文献で見つけることができますが、アルゴリズムの一般的な本質は非常に簡単です:
- パラメーターの初期値でモデルを初期化します。
- E-ステップ。 潜在変数を現在のモデルの期待値で埋めます。
- Mステップ。 潜在変数が固定されたモデルの尤度を最大化します。 たとえば、パラメータの勾配降下。
- 潜在変数の期待値が変化しなくなるまで、(2、3)を繰り返します。
M-ステップが最後まで尤度を最大化せず、最大に向かって一歩しか踏み出さない場合、これは一般化EM(GEM)と呼ばれます。
EMを使用したPCAソリューション
PCA EMモデルの最適なパラメーターの検索にアルゴリズムと最尤法を適用します
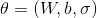
モデル。 観測可能なパラメータと潜在的なパラメータの結合尤度は、次のように記述できます。
どこで
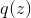
任意の分布です。 次に、式を容易にするためにパラメーター分布の規則を省略します。
大きさはどこですか

呼ばれた
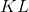
分布間の相違
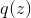
そして

。 価値

エントロピーと呼ばれる
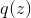
。
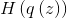
パラメータに依存しない
、最適化中にこの用語を無視できます。
価値
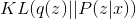
非負でゼロの場合
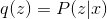
。 この点で、次のEMアルゴリズムを定義しましょう。
- E:
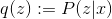 。 これにより、2番目の用語が無効になります
。 これにより、2番目の用語が無効になります 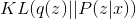 。
。 - M:最初の項を最大化する
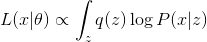 。
。
PPCAは線形モデルであるため、分析的に解決できます。 しかし、代わりに、最大化が最後まで実行されず、勾配上昇が最適に向かって1ステップしかない場合、一般化されたEMアルゴリズムの助けを借りてそれを解決しようとします。 さらに、確率的勾配上昇を使用します。 彼のステップは、平均的にのみ最適化へのステップになります。 データはiidなので、
フォームの式に注意してください
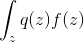
数学的な期待です
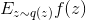
。 それから
単一のサンプルは数学的な期待の公平な推定値であるため、次の等式をほぼ書き留めることができます。
合計、置換
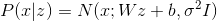
私達は得る:
または
フォーミュラ1. PPCAモデルのデータの尤度に比例する損失関数。
どこで
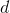
-観測された変数の次元

。 それでは、PPCAのGEMアルゴリズムを書きましょう。
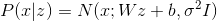
、そして
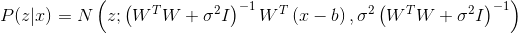
。 GEMアルゴリズムは次のようになります。
- パラメータを初期化する
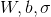 合理的なランダム初期近似。
合理的なランダム初期近似。 - サンプリング
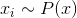 -データからのミニバッチのサンプリング。
-データからのミニバッチのサンプリング。 - 潜在変数の期待値を計算します
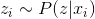 または
または 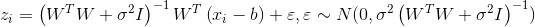 。
。 - 代用
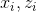 式(1)で
式(1)で 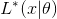 そして、パラメータの勾配上昇のステップを踏みます。 覚えておくことが重要です
そして、パラメータの勾配上昇のステップを踏みます。 覚えておくことが重要です 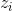 入力として取得し、その内部のエラーの逆伝播を許可しないでください。
入力として取得し、その内部のエラーの逆伝播を許可しないでください。 - データの尤度とコントロールの可視変数の潜在変数の期待値が大きく変わらない場合、トレーニングを停止します。 それ以外の場合は、手順(2)に進みます。
モデルがトレーニングされた後、モデルからサンプルを生成できます。
PCA問題の数値解
標準のSGDを使用してPPCAモデルをトレーニングしましょう。 すべての詳細を理解するために、おもちゃの例を使用してモデルの動作を再度調べます。 完全なモデルコードについては、
こちらをご覧ください 。この記事では、重要な点のみを取り上げます。
置く
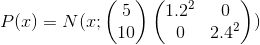
-対角共分散行列を使用した2次元正規分布。
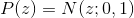
-1次元の通常の潜在表現。
図 1.分布の点の95%が入る中央付近の楕円

。
そのため、最初に行うことはデータの生成です。 サンプルを生成します

:
def normal_samples(batch_size): def example(): return tf.contrib.distributions.MultivariateNormalDiag( [5, 10], [1.2, 2.4]).sample(sample_shape=[1])[0] return tf.contrib.data.Dataset.from_tensors([0.]) .repeat() .map(lambda x: example()) .batch(batch_size)
次に、モデルパラメーターを決定する必要があります。
input_size = 2 latent_space_size = 1 stddev = tf.get_variable( "stddev", initializer=tf.constant(0.1, shape=[1])) biases = tf.get_variable( "biases", initializer=tf.constant(0.1, shape=[input_size])) weights = tf.get_variable( "Weights", initializer=tf.truncated_normal( [input_size, latent_space_size], stddev=0.1))
その後、可視変数のサンプルの潜在表現を取得できます。
def get_latent(visible, latent_space_size, batch_size): matrix = tf.matrix_inverse( tf.matmul(weights, weights, transpose_a=True) + stddev**2 * tf.eye(latent_space_size)) mean_matrix = tf.matmul(matrix, weights, transpose_b=True)
ここでは、tf.stop_gradient(...)に注意する必要があります。 この関数は、入力サブグラフ内のパラメーター値がこれらのパラメーターに関して勾配に影響を与えることを許可しません。 それが必要です
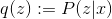
EMアルゴリズムが正しく機能するために必要なMステップの間、固定されたままでした。
損失関数を書きましょう
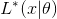
Mステップでの最適化:
sample = dataset.get_next() latent_sample = get_latent(sample, latent_space_size, batch_size) norm_squared = tf.reduce_sum((sample - biases - batch_matmul(weights, latent_sample, batch_size))**2, axis=1) loss = tf.reduce_mean( input_size * tf.log(stddev**2) + 1/stddev**2 * norm_squared) train = tf.train.AdamOptimizer(learning_rate) .minimize(loss, var_list=[bias, weights, stddev], name="train")
したがって、モデルはトレーニングの準備ができています。 モデルの学習曲線を見てみましょう。
図 2.曲線学習モデルPPCA。
モデルはかなり定期的かつ迅速に収束することがわかります。これはモデルの単純さをよく反映しています。 学習した分布パラメーターを見てみましょう。
図 3.原点からのオフセットのグラフ(パラメーター
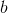
)
それが見られる
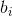
分析値に迅速に収束
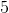
そして

。 オプションを見てみましょう
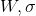
:
図 4.パラメータ変更のスケジュール

。
値が見られます

1.2に収束、つまり 予想どおり、入力分布のより小さい偏差軸に。
図 5.パラメーター変更のグラフ
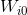
。
、順番に、おおよその値になりました
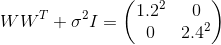
。 これらの値をモデルに代入すると、次のようになります
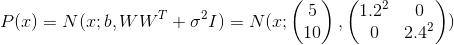
、これはデータの分布を復元したことを意味します。
データの分布を見てみましょう。 潜在変数は1次元であるため、1次元分布として表示されます。 可視変数は2次元ですが、与えられた共分散行列は対角です。つまり、その楕円体は座標軸と整列しています。 したがって、座標軸上の分布の2つの投影として表示します。 これは、与えられ学習された分布がどのように見えるかです

最初の座標軸への投影:
図 6.特定の分布の予測

最初の座標軸上。
図 7.学習した分布の予測
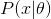
最初の座標軸上。
そして、与えられて学習された分布は次のようになります

2番目の座標軸への投影:
図 8.特定の分布の予測

2番目の座標軸へ。
図 9.学習した分布の予測
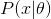
2番目の座標軸へ。
したがって、分析および学習分布は次のようになります
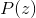
:
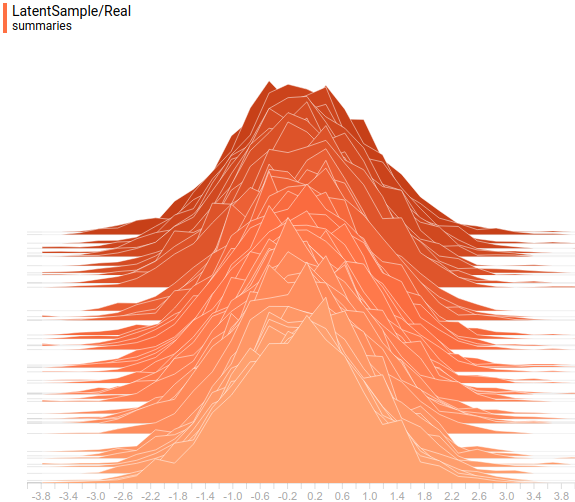
図 10.ターゲット配布
。
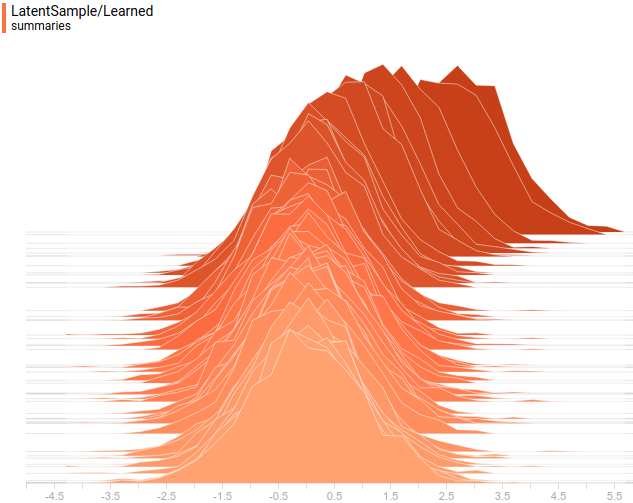
図 11.学習した分布

。
学習されたすべての分布は、タスクによって与えられた分布に非常に類似した分布に収束することがわかります。 これを最終的に確認するために、モデルトレーニングのダイナミクスを見てみましょう。
図 12. PPCAモデルの学習プロセス。学習された分布

データ分布に収束

。
おわりに
指定されたモデルは、線形モデルである古典的なPCAモデルの確率的解釈です。
元の記事の数学を使用し、その上にGEMアルゴリズムを構築し、簡単な例を使用して、結果のモデルが分析解に収束することを示しました。 もちろん、問題がある場合

正常ではありませんでした。モデルはそれほどうまくいかなかったでしょう。 PCAが特定の超平面にないデータを完全に処理しないのと同じように。 分布を近似するより複雑な問題を解決するには、より複雑で非線形のモデルが必要です。 そのようなモデルの1つである生成的敵対ネットワークについては、次の記事で説明します。
謝辞
テキストを
レビューしてくれた
Olga Talanovaに感謝します。 この記事のレイアウトを手伝ってくれた
Andrei Tarashkevichに感謝します。