リチャード・ハミング：第9章N次元空間

こんにちは、Habr。 「You and Your Work」という素晴らしい記事（+219、2222ブックマーク、350k読み取り）を覚えていますか？

そのため、ハミング（はい、はい、自己チェックと自己修正のハミングコード ）には、彼の講義に基づいて書かれた本があります。 男性がビジネスを話しているため、ここで翻訳しています。

この本はITだけでなく、信じられないほどクールな人の思考スタイルに関する本です。 「これは単なる肯定的な思考の責任ではありません。 素晴らしい仕事をする可能性を高める条件を説明しています。」

すでに6（30から）の章を翻訳しています。

第9章N次元空間

（翻訳のおかげで、アレクセイ・フォーキン、「前の章」で私の電話に答えてくれました。）翻訳を手伝いたい人は-個人のメールまたはmagisterludi2016@yandex.ruに書いてください

主に数学研究部門でベル電話研究所で30年間積極的に研究した後、教授になったとき、教授は過去の経験を振り返り、要約する必要があることを思い出しました。 私はテーブルに足を置き、私の過去を熟考し始めました。 初期の頃、私は主にコンピューティングに従事していました。つまり、コンピューティングを必要とする多くの大規模プロジェクトに関与していました。 私が部分的に関与していたいくつかの大規模なエンジニアリングシステムがどのように開発されたかを考えて、私はそれらから少し離れて、それらが多くの共通要素を持っていることを確認し始めました。 時間が経つにつれて、設計タスクがn次元空間にあることに気付き始めました。ここで、nは独立したパラメーターの数です。 はい、3次元のオブジェクトを作成しますが、その設計は多次元空間にあり、各投影パラメーターに対して1次元です。

厳密な詳細なしにさらなる証拠が直感的になるように、多次元空間が必要になります。 したがって、ここでn次元空間を検討します。

あなたは三次元空間に住んでいると思いますが、多くの場合、二次元空間に住んでいます。 たとえば、人生のランダムな過程で、誰かに会った場合、この人に再び会う合理的なチャンスがあります。 しかし、3次元の世界では、このチャンスはありません！ 潜在的に3次元で生きる海の魚を考えてみましょう。 表面または底に沿って移動し、物事を2次元に制限するか、ジャムを形成するか、河口、ビーチ、サルガッソー海などの1つの場所に同時に集まります。 3次元で外洋をさまよいながら、仲間と出会うことは期待できません。 または、たとえば、飛行機を衝突させたい場合は、空港の近くでそれらを収集し、2次元の飛行レベルに配置するか、グループとして送信する必要があります。 本当にランダムなフライトでは、現在発生しているよりもクラッシュが少なくなります！

N次元空間は、設計上の問題を解決するときにそこを歩き回ったときに何が起こるかを理解するために探索する必要がある数学的な構造です。 2次元では、ピタゴラスの定理があります;直角三角形の場合、斜辺の二乗は他の辺の二乗の合計に等しくなります。 三次元では、平行六面体の対角線の長さに興味があります。図 9.1。 それを見つけるには、まず1つの面の対角線を描き、ピタゴラスの定理を適用してから、それを3次元の反対側の側面の1つとして取り、それを垂直にします、そして再びピタゴラスの定理から、対角線の正方形は3つの垂直な辺の平方の合計です 明らかに、この証明と式の必要な対称性から、より高い次元に上っても、対角線の正方形は相互に垂直な辺の正方形の合計に等しくなるということから、



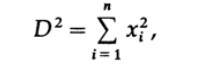
ここで、x _iは、 n次元空間の長方形ブロックの辺の長さです。


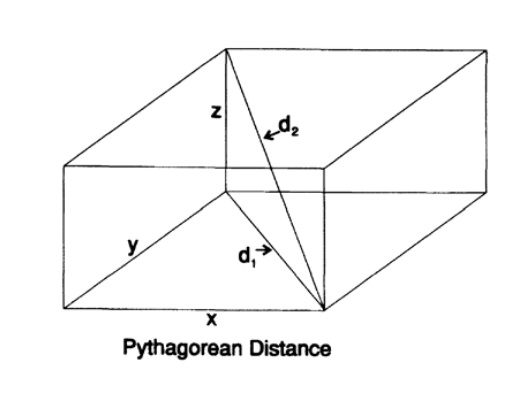図 9.I

幾何学的アプローチを続けると、空間内の平面は単純な線形結合x _iになり、ポイントの周りの球体は、与えられたものから一定の距離にあるすべてのポイントになります。

限られた空間の大きさの概念を理解するには、n次元の球の体積が必要です。 しかし、最初に、n！のスターリングの近似が必要です。これにより、詳細のほとんどを理解し、次のことの正確性を確認し、言葉を受け取らないようにします。

タイプnの製品で！ 処理が難しいため、log n！を使用します。



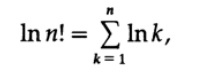
ここで、もちろん、lnはeの底対数です。 合計は、積分に関連していることを思い出させるので、そのような積分から始めます



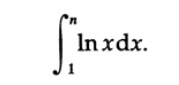
部分ごとの統合を適用します（ln xは代数関数の統合に由来するため、次のステップで除外できることがわかっているため）。 U = ln x、dV = dx、そして



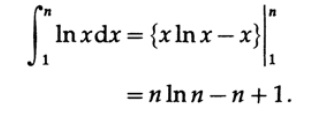
一方、得られた積分ln xに台形公式を適用すると、図を参照してください。 9.II、



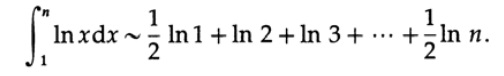
ln 1 = 0なので、等式の両側に（1/2）* ln nを追加すると、最終的に



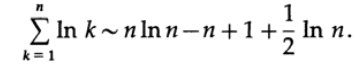
eを両方の部分の累乗に上げることにより、対数を取り除きます。



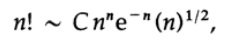
ここで、Cはnに依存しない一定の定数（eに近い）です。台形との積分を近似しているため、nの増加に伴って誤差はますますゆっくりと大きくなります。


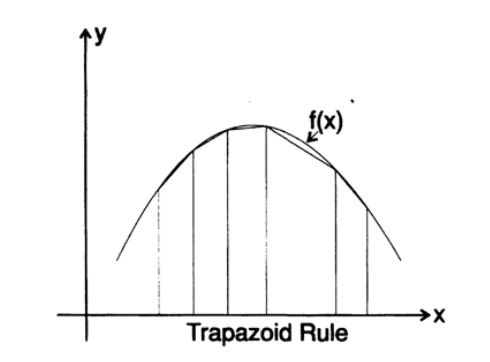図 9.II

ますます、Cには制限があります。 これは、スターリングの公式の最初の形式です。 無限大になる傾向がある定数Cの制限を計算するのに時間を浪費しません。これは√（2 *π）= 2.5066 ...（e = 2.71828 ...）になります。 したがって、最終的に階乗のスターリング公式を取得します



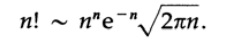
次の表に、n！のスターリング近似の誤差を示します。



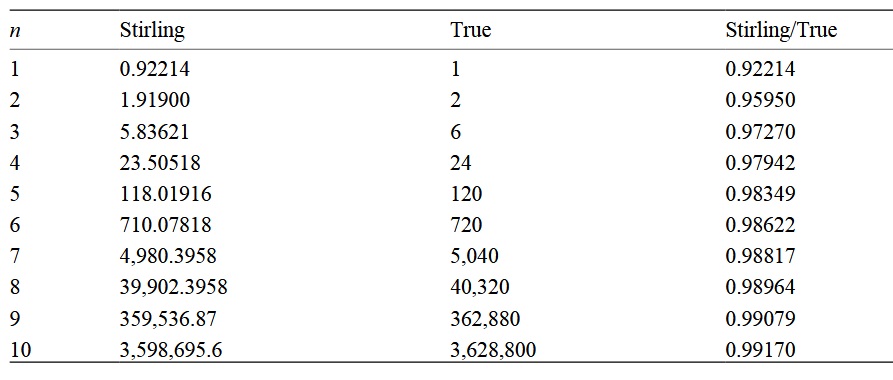
数値が増加すると、係数は1に近づきますが、差はますます大きくなることに注意してください。

2つの機能を検討する場合



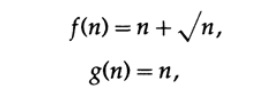
nが無限大になる傾向がある比率f（n）/ g（n）の制限は1ですが、表のように、差



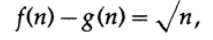
nの増加とともにますます大きくなります。

階乗の概念をすべての正の実数のセットに拡張する必要があります。これのために、積分の形でガンマ関数を導入します



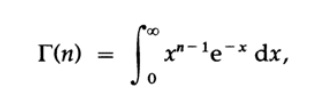
これはすべてのn> 0に存在します。 n> 1の場合、パーツごとに統合します。今回はdV = e ^（-x）dxおよびU = x ^（n-1）を使用します。 2つの制限の場合、積分可能な部分は0であり、次の式があります



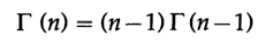
Γ（1）= 1の場合

したがって、ガンマ関数は値（n-1）を取ります！ すべての正の整数nについて、すべてのn> 0に対して積分が存在するため、階乗の概念をすべての正の数に自然に拡張します。

必要になります



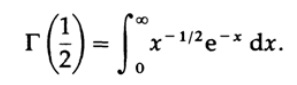
x = t ^ 2、次にdx = 2t * dtを表すと、次のようになります（最後のステップで対称性を使用）



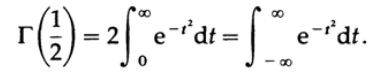
次に、標準的なアプローチを使用して、この積分を計算します。 2つの積分の積を取得します。1つは変数xに関するもので、もう1つは変数yに関するものです。



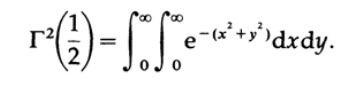
x ^ 2 + y ^ 2は極座標を意味するため、



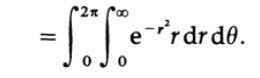
曲線積分（角度積分）は簡単です。 指数関数的統合も簡単になりました。



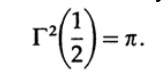
このように



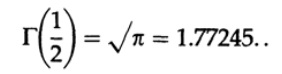
次に、次元球（または必要に応じて超球）のボリュームnに戻ります。 辺xのn次元立方体の体積がx ^ nであることは明らかです。 少し考えてみると、n次元球体の体積の式は次の形式になっているはずです。



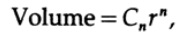
ここで、C _nは対応する定数です。 n = 2の場合、定数はπ、n = 1の場合、2です（考えてみれば）。 3次元の場合、C ₃ = 4 *π/ 3です。

1/2のガンマ関数に使用したのと同じトリックから始めますが、今回はそれぞれが独自の変数x _iを持つn個の積分の積を取ることを除きます。 球の体積は、表面の体積の合計として表すことができます。この合計の各項は、表面積に厚さdrを掛けた値に対応します。 球体の場合、表面積の値は、半径rに対して球体の体積を微分することで取得できます。



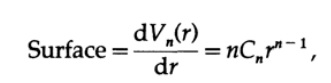
したがって、ボリュームの条件は等しい



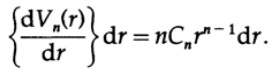
r ^ 2 = tを等式すると、




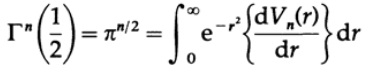
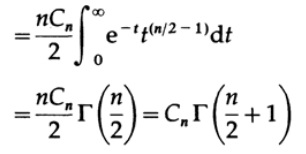
どこから入手しますか。



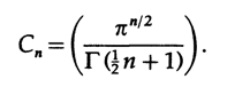
わかりやすい



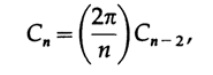
そして、次の表を計算できます。



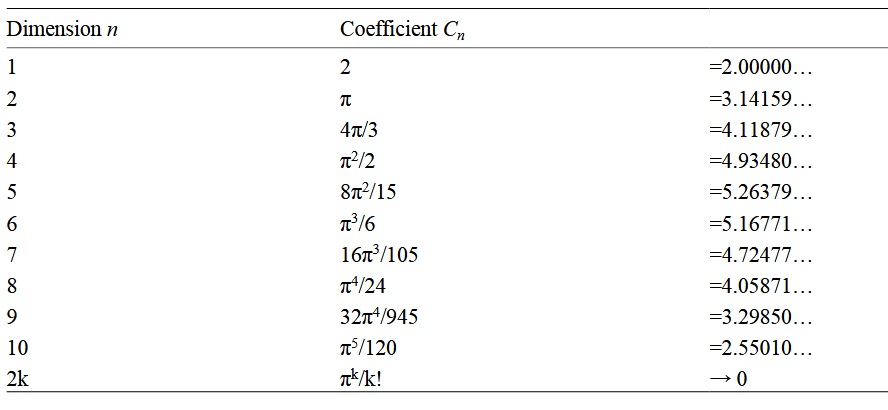
したがって、係数C _nはn = 5に増加し、その後0に減少することがわかります。単位半径の球体の場合、これは球体の体積が次元の増加とともにゼロになる傾向があることを意味します。 半径がrの場合、便宜上、ボリュームに対してn = 2kを示します（nが増えると実数は滑らかに変化し、奇数次元の球は計算が難しくなるため）。


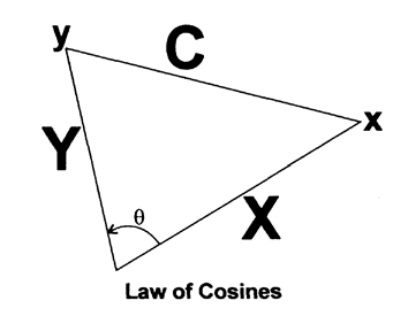図 9.III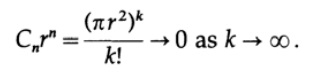



半径rがいくら大きくても、測定回数nを増やすと、球体の体積が任意に小さくなります。

ここで、n次元の球体の表面近くに位置する体積の相対的な量を検討します。 rを球の半径、表面の内側半径をr（1-ε）とすると、表面の相対体積は



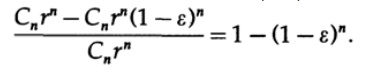
nが大きい場合、その内側の表面が（半径に対して）どんなに薄くても、ほとんど何もありません。 私たちが言うように、ボリュームはほとんどすべて表面にあります。 3次元空間でも、1つの球体は表面の内側に7/8の体積を持ち、厚さは1/2半径です。 n次元空間では、1-（1/2）^ nは表面の半径の半分の内側にあります。

これは設計上重要です。 上記の計算とデータ変換の後、ほぼ確実に最適な設計が表面上にあり、あなたが思うほど深くないことがわかります。 計算手法は通常、多次元空間で最適なものを見つけるのに適していません。 これはまったく奇妙ではありません。 一般的に言えば、最良の設計は、1つまたは複数のパラメーターを極端なものにすることです。設計の可視領域の表面にいるのは明らかです。

次に、n次元の立方体の対角線、つまり、原点から座標（1,1、...、1）を持つ点までのベクトルを考えます。 この線と任意の軸の間の角度のコサインは、この軸への投影の長さの座標値の比として定義によって与えられます。これは明らかにベクトルの長さ√nに対する1です。 だから



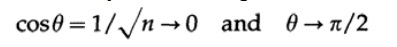
nが大きい場合、対角線は各座標軸にほぼ垂直になります！

座標（±1、±1、...、±1）を持つポイントを考慮すると、すべてが各座標軸にほぼ垂直になるように2n対角線が存在します。 たとえば、n = 10の場合、その数はほぼ垂直な線である1024です。

2つのベクトル間に角度が必要です。これはベクトルのスカラー積であることを覚えているかもしれませんが、何が起こっているかをよりよく理解するために、もう一度印刷することをお勧めします。 [備考; 何が起こっているのかを感じるために、すべての基本的な推論を修正することは、重要な状況で非常に有用であることがわかりました。] 図 9.III。 3点x、yおよび原点の平面に余弦定理を適用すると、次のようになります。



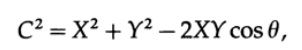
ここで、XとYは、点xとyまでのセグメントの長さです。 ただし、Cは各軸の座標の差を使用して取得できます



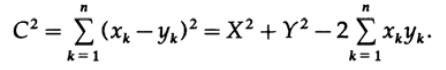
表示される2つの式を等しくする



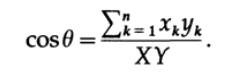
原点から描画された2つのセグメントにこの式を適用し、座標セットのランダムポイントに

（±1、±1、...、±1）

ランダムに取られたこのような2つの要因のスカラー積は再び±1であり、これをn回合計する必要がありますが、各セグメントの長さは√nです（したがって、分母のnに注意）



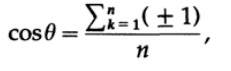
そして、大きな数の弱い法則により、nがほぼ確実に増加するにつれて、これは0になる傾向があります。 しかし、2 ^ n個のランダムなベクトルがあり、与えられたベクトルに対して、残りの2 ^ n個のランダムなベクトルはほぼ確実にこれにほぼ垂直です！ n次元は本当に広大です！

線形代数や他の分野では、多くの垂直軸を見つけて、この座標系で他のすべてを表すことを学びましたが、n次元空間では、相互に垂直なn座標軸を見つけた後、他の方向が2 ^ nあることがわかります見つけたものにほぼ垂直！ 線形代数の理論と実践は完全に異なります！

最後に、n次元空間についての直感があまり良くないことをさらに証明するために、次の章で必要になる別のパラドックスを作成します。 まず、4x4の正方形を4つの単位の正方形で割って、それぞれに単位円を描きます。図 9.IV. 次に、正方形の中心を中心とする円を描き、内側から残りの部分に触れます。 その半径は図からでなければなりません。 9.IV、



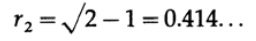
3次元空間には、4x4x4立方体と単位半径の8つの球があります。 中心を結ぶセグメント上にある点で残りの部分に接する内側の球は半径を持ちます



その半径が2次元より大きい理由を考えてください。

n次元に移動すると、4x4x ... x4立方体と2 ^ nの球体があり、それぞれが各コーナーにあり、それぞれが他のn個の隣接する球体に接触しています。 残りの内側から接触する内側の球体には半径があります



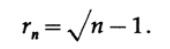
注意深くチェックしてください！ よろしいですか そうでない場合は、なぜですか？ 推論の間違いはどこにありますか？
これが正しいことを確認した後、n = 10測定の場合に適用できます。 内側の球には、半径があります





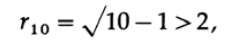
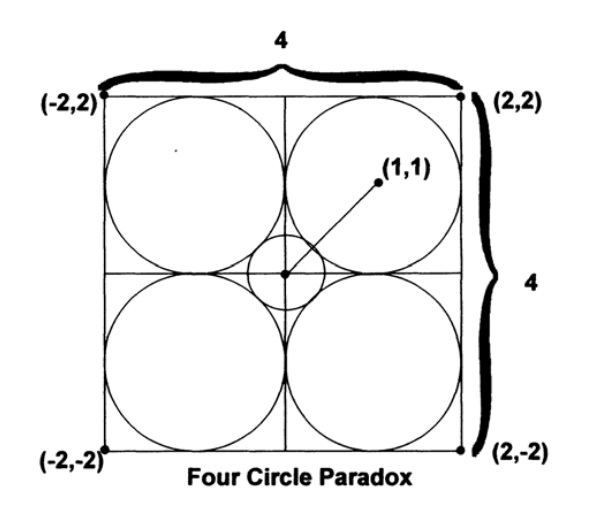図 9.IV

そして、10次元空間では、内側の球体が立方体を超えました。 はい、球体は凸面です、はい、それは内側から残りの1024に触れ、同時に立方体を越えます！

これは、n次元空間についての繊細な直感には多すぎますが、n次元空間は通常、複雑なオブジェクトが設計される場所であることを忘れないでください。 n次元空間をよりよく感じて、今説明したことを考え、それがどのように成り立つのか、あるいはなぜそれが成り立つべきなのかを理解するまで試してみてください。 そうしないと、複雑な設計の問題を解決するときに問題が発生します。 おそらく、異なる次元の半径を再計算し、対角線と座標軸の間の角度に戻り、それがどのようになるかを確認する必要があります。

ここで、ピタゴラス距離を使用して古典的なユークリッド空間でこれをすべて行ったことに厳密に注意する必要があります。ピタゴラス距離では、対応する座標の差の平方の合計は点間の距離の平方に等しくなります。 数学者はこの距離をL ₂と呼びます。

空間L ₁は、座標差の平方の合計ではなく、距離の合計を使用します。まるで、長方形のストリートグリッドのある都市を旅しているようです。 これは、2つのポイント間の差の合計であり、どこまで行かなければならないかを示します。 コンピューティング業界では、後続の章で明らかになる理由から、これを「ハミング距離」と呼ぶことがよくあります。 この空間では、2次元の円は上に立つ正方形のように見えます、図 9.V. 3次元空間では、立方体が上に立っているようなものです。 これで、上記の例の逆説的な内部球がどのように立方体を越えることができるかをよく見ることができます。

_L∞またはチェビシェフ距離と呼ばれる、よく使用される3番目のメトリック（すべてメトリック=距離関数）があります。 ここでは、他の違いに関係なく、距離に対して最大の座標差が取られます。図 9.VI. この空間では、円は正方形、3次元の球体は立方体です。この場合、パラドックスの内側の球体はすべての方向で半径がゼロであることがわかります。

これらはメトリックの例、距離の尺度でした。 2つのポイントxとyの間のメトリックD（x、y）を決定するための条件は次のとおりです。

1. D（x、y）≥0（非負）
2. x = y（恒等式）の場合にのみ、D（x、y）= 0
3. D（x、y）= D（y、x）（対称性）
4. D（x、y）+ D（y、z）≥D（x、z）（三角形の不等式）。



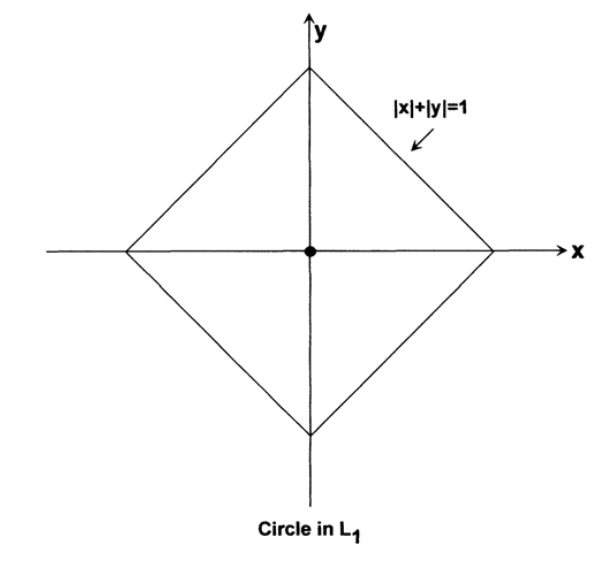図 9.V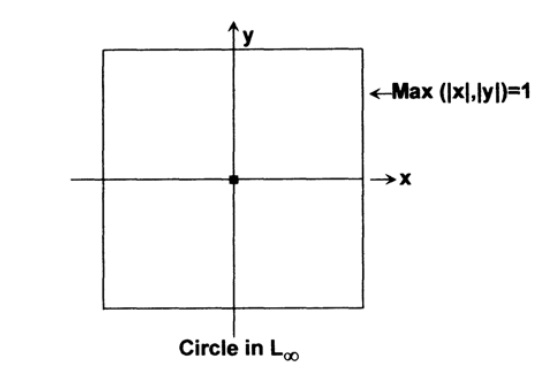



図 9.VI

3つのメトリック_L∞ 、L ₂ 、L ₁ （チェビシェフ、ピタゴラス、ハミング）がすべてこれらの条件を満たすことを確認します。

真実は、さまざまな座標の複雑な設計では、これらのメトリックを組み合わせて使用​​できるため、設計スペースは完全な図ではなく、ピースとパーツの混合であるということです。 L ₂メトリックは明らかに最小二乗に関係しており、他の2つの_L∞とL _1は比較により類似しています。 実生活での比較では、通常、任意の1つの特性の最大差_L∞を2つのオブジェクトを区別するための十分な条件として使用するか、ビット列のように、これは不一致の数であり、これは有意であり、平方和が適合しないことを意味しますそのL ₁メトリックが使用されます。 これは、AIのパターンを識別する場合により当てはまります。

残念ながら、上記のすべてが真実ですが、それがめったに明らかにされません。 誰も私に言ったことはありません！ 次の章で多くの結果が必要になりますが、一般に、このデモンストレーションの後、複雑な設計と、設計が実行されるスペースの徹底的な分析のために、以前よりも準備を整える必要があります。 混乱は基本的にデザインの出番であり、許容できる解決策を見つける必要があります。

L ₁と_L∞はあまり知られ_ていないので、3つの指標についていくつか説明します。 L _2は、物理的測定値からデータを抽出するなど、物理的および幾何学的なケースで使用するための自然な距離関数です。 したがって、物理学ではどこでもL ₂を見つけることができます。 しかし、知的判断に関しては、他の2つの指標がより適切ですが、これはゆっくりと認識されます。そのため、他のより適切な推定値を使用する必要がある場合、明らかにL2の測定値であるカイ2乗推定値を頻繁に使用することがわかります。

継続するには...

誰が翻訳を手伝いたいのか-個人のメールまたはメールに記入してくださいmagisterludi2016@yandex.ru