はじめに

あなたと私が石の飛行よりも深刻な何かをモデル化するのに十分な経験を得たことを願っています。 私はそのような仕事を提案します

球形核を発射する銃は、400 m / sの初期速度を与えます。 地平線に対して35度の角度で発射するときの発射体の軌道を決定します。 重力場は均質であると考えられ、地球の曲率を無視する必要があります。

これは間違った問題の例です。 第一に、私たちが考慮に入れていると言われていない、または空気抵抗を考慮していない。 そして、考慮に入れると、問題には明らかにパラメーターが欠けています。 残念ながら、この種の問題ステートメントは非常に一般的です。 したがって、両方のケースの問題を解決し、必要なパラメーターを自分で入力します。 同時に、新しいことを学びます。 行こう！

1.設計スキーム

過去において、私はあなたの想像力を訓練するための計画を意図的に描きませんでした。 石が垂直に落ちるのは簡単に想像できます。 これで、タスクはより複雑になり、図面なしではできません。



このような図面は、デザインスキームと呼ばれます-プロセスまたはオブジェクトの条件付きグラフィックイメージで、タスクに入力された仮定を考慮して作成されます。

この図は、発射体の任意の位置を示しており、移動の開始からしばらくしてから落下する位置になっていることに注意してください。 ダイナミクスの問題では、力ベクトルの相対位置を想像し、それらを軸方向の投影に正しく分解する方が便利です。 初期位置で示した唯一のものは、初期速度ベクトルです。 これは、初期条件を設定するときに役立ちます。

2.問題の形式化（耐環境性を除く）

すべてが微分方程式のシステムをコンパイルする準備ができています

$$

$$\ begin {align}＆m \、\ ddot x = 0 \\＆m \、\ ddot y = -m \、g \ end {align}$$

空気抵抗は考慮されておらず、力は1つしかありません。x軸にはゼロ、y軸にはマイナスの真の値が投影されます。 結局、重力場は均一であり、地球は平らであるという仮定を受け入れました。 したがって、重力は常に一定であり、垂直下向きに向けられます。 ご覧のとおり、ここでは質量に依存するものはなく、両方の方程式で質量が減少します

$$

$$\ begin {align}＆\ ddot x = 0 \\＆\ ddot y = -g \ end {align}$$

結果の2つの2次方程式のシステム。 彼女をコーシーの形にする必要があります。 それを覚えていますか？ 覚えているなら、ネタバレを見ずに自分でやってみてください

3.オクターブスクリプト、または同じ仕事を二度としない方法

前回 、Octaveコンソールにコマンドを直接入力しました。 まあ、私たちの仕事は小さかった。 そして、もし大きいなら？ そして、あなたが設定を変更したい場合は？ そして、あなたが延期された仕事に戻りたいなら？ そして...要するに、プログラムをOctaveに保存できるのは良いことです。 それでも、不可能なことは何もありません。

画面の下部のコマンドウィンドウの下には、コマンドウィンドウ、エディター、ドキュメントのタブがあります。 [エディター]タブが必要です。 これはm言語のスクリプトエディターです。 このタブを開き、次のテキストを入力します。

%------------------------------------------------------------------------------- % %       %    % %------------------------------------------------------------------------------- function dYdt = f(Y, t) g = 9.81; %    dYdt(1) = Y(3); % dx/dt = vx dYdt(2) = Y(4); % dy/dt = vy dYdt(3) = 0; % dvx/dt = 0 dYdt(4) = -g; % dvy/dt = -g endfunction 

これは、m言語の関数として設計された問題で、発射体の運動の微分方程式系の右側にすぎません。 意味は前回と同じです。 今だけ4つの方程式があります。 さて、通常の大人サイズの自由落下の加速を行います。 このファイルをfmという名前でディスクに保存します

注意！ m言語の各関数は、その名前が関数の名前と一致する独自のファイルに保存する必要があります。 この場合、関数の名前はfです。つまり、ファイルの名前はfです。



「％」で始まる行は何ですか？ そして、これら、アパッチ兄弟はコメントです！ Octaveでこの文字の前にあるテキストは、インタープリターによって無視されます。 コメントするだけでなく、プログラムを使用したい他の人は言うまでもなく、少なくとも自分自身を方向付けるためにプログラムを提供する必要があります。

そこで、オクターブ方程式系を設定します。 新しいファイルを作成し、ballistics.mなどの名前を付けて、以前のファイルを保存したのと同じ場所に保存します。 問題の解決を始めましょう！

 %------------------------------------------------------------------------------- %   %------------------------------------------------------------------------------- %    v0 = 400; %       alpha = 35 * pi / 180; %------------------------------------------------------------------------------- %   %------------------------------------------------------------------------------- x0 = 0; y0 = 0; vx0 = v0 * cos(alpha); vy0 = v0 * sin(alpha); Y0 = [x0; y0; vx0; vy0]; %------------------------------------------------------------------------------- %    %------------------------------------------------------------------------------- %    t0 = 0; %    tend = 10.0; %    deltaT = 0.1; %      t = [t0:deltaT:tend]; %     Y = lsode("f", Y0, t); %     plot(Y(:,1), Y(:,2)); 

ほとんどの操作の意味はコメントから明らかです。 初期条件について個別に説明します。 4つの位相座標があります：発射体の2つのデカルト座標、座標軸上の2つの速度の投影

$$

$$\ begin {align}＆Y（1）\ to x（t）\\＆Y（2）\ to y（t）\\＆Y（3）\ to v_x（t）\\＆Y（4）\ to v_y（ t）\ end {align}$$

位相座標ごとに、それらの初期値を設定する必要があります。 原点に初期位置を設定することは論理的です。 他の2つの変数を振るのは、注意、 xおよびy軸上の速度ベクトルの投影の初期値です 。 次に、軸上の投影を見つけやすいように初期速度ベクトルを描画しました

$$

$$\ begin {align}＆v_x = v_0 \、\ cos \ alpha \\＆v_y = v_0 \、\ sin \ alpha \\ \ end {align}$$

これですべて準備が整いました。 歯車と黄色の三角形のボタンをクリックして、スクリプトを開始します。 応答として、システムはウィンドウを表示します



スクリプトの検索パスにスクリプトが存在するパスを追加するように求められます。 これは、スクリプトをエディターにロードするか、新しいスクリプトを作成した後に一度実行する必要があります。 「追加...」ボタンをクリックして、結果を取得します



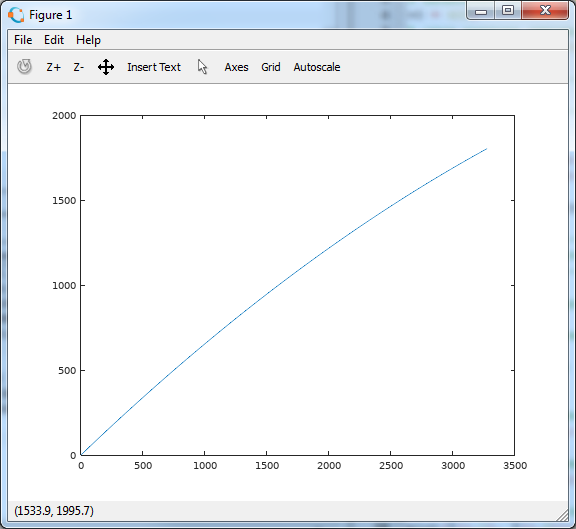
有望に見えます。 10秒という時間では、衣装を着陸させるのに十分ではありません。 傾向値を変更し、同様の画像が得られるまでスクリプトを再度実行します



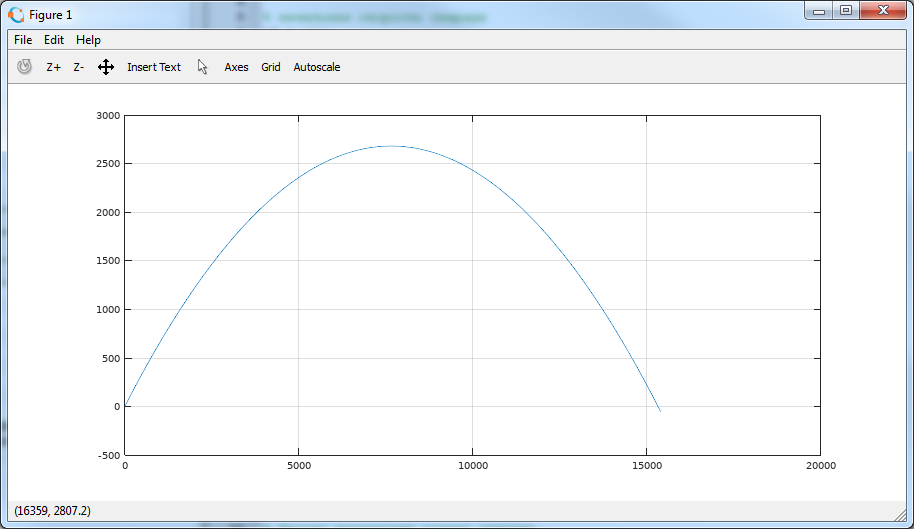
対応する傾向= 47秒。 シミュレーションは終了し、シェルはx軸より下を飛行しましたが、これは正常です。サーフェスとの遭遇をシミュレートできないためです。

4.問題の形式化（媒体の抵抗を考慮に入れる）

シェルの形状としてのボールは、偶然ではありません。 それをねじらないように、それはすべての側面に同じ断面を持っています-円（ところで、ボストーク宇宙船は球形の降下ビークルと同じ形状でした）。 したがって、気流をどのように方向付けても、周りを流れるとき、運動に対する抵抗力は同じで等しくなります

$$

$$R = c_f \、S \、\ frac {\ rho \、v ^ 2} {2}$$

ここで、c _f = 0.47は金型の抗力係数です。 Sは断面積です。 $$$\ rho$ = 1.29 kg / m ³は空気の密度です。 vは入射流の速度、この場合は発射体の速度です。

ドラッグベクトルは常に速度ベクトルに対して向けられます。 したがって、設計スキームを再描画します



どの時点でもベクトルが $$$\ vec R$ スピードに反対？ とても簡単です。 速度ベクトルは軌跡に正接していることがわかります。 ベクターを導入 $$$\ vec \ tau$ 長さが1で、速度が向けられているのと同じ場所に向けられます。 次に、ベクトル $$$\ vec R$ ベクトルの観点から表現できる $$$\ vec \ tau$ および抵抗係数

$$

$$\ vec R =-R \、\ vec \ tau$$

ベクトルを見つける方法 $$$\ vec \ tau$ ？ 非常にシンプルで、座標軸上の投影は等しくなります

$$

$$\ begin {align} \ tau_x = \ frac {v_x} {v} \\ \ tau_y = \ frac {v_y} {v} \ end {align}$$

速度ベクトルのモジュラスは、その投影を通して簡単に表現されます

$$

$$v = \ sqrt {v_x ^ 2 + v_y ^ 2}$$

座標軸上の空気抵抗力ベクトルの投影は計算が簡単です

$$

$$\ begin {align}＆R_x =-R \、\ tau_x = -R \、\ frac {v_x} {v} =-\ frac {1} {2} \、c_f \、S \、\ rho \、v \、v_x \\＆R_y =-R \、\ tau_y = -R \、\ frac {v_y} {v} =-\ frac {1} {2} \、c_f \、S \、\ rho \、v \ 、v_y \\ \ end {align}$$

そしてそれは運動方程式を変える

$$

$$\ begin {align}＆m \、\ ddot x =-\ frac {1} {2} \、c_f \、S \、\ rho \、v \、v_x \\＆m \、\ ddot y =-\ frac {1} {2} \、c_f \、S \、\ rho \、v \、v_y-m \、g \ end {align}$$

今、質量を減らさないのは何ですか？ はい、発射体のダイナミクスは質量に依存します。 しかし、質量による除算を禁止する人はいません。両方の方程式をそれに分けます

$$

$$\ begin {align}＆\ ddot x =-k \、v \、v_x \\＆\ ddot y =-k \、v \、v_y-g \ end {align}$$

どこで

$$

$$k = \ frac {c_f \、S \、\ rho} {2 \、m}$$

発射体の加速に対する抵抗力の寄与を決定する係数。 シェルがボールであることを覚えていれば、大幅に簡素化できます

$$

$$m = \ gamma \、V = \ gamma \、\ frac {4} {3} \、\ pi \、r ^ 3、\ quad S = \ pi \、r ^ 2$$

最初の式はボールの質量であり、ここで $$$\ガンマ$ コアの元となる材料の密度です。rはコアの半径です。 2番目の式は、ボールの断面積です。 これらの式を係数の式に代入し、単純化します

$$

$$k = c_f \、\ rho \ frac {\ pi \、r ^ 2} {\ frac {8} {3} \、\ gamma \、\ pi \、r ^ 3} = \ frac {3} {8 } \、\ frac {c_f \、\ rho} {r \、\ gamma} = \ frac {3} {4} \、\ frac {c_f \、\ rho} {d \、\ gamma}$$

ここで、dはコアの直径、つまり銃の口径です。 この式から、口径が大きく、発射体の材料が濃いほど、空気抵抗の影響が小さくなることがすでにわかっています。

発射物のパラメーターを設定しましょう。 ballistics.mファイルの最後に次の行を追加します

 %------------------------------------------------------------------------------- %   %------------------------------------------------------------------------------- %    global gamma = 7800; %    ( ) global c_f = 0.47; %  global d = 0.1; 

コアを口径100 mmの鋳鉄にします。 各変数の前にどのような単語がグローバルであるか。 したがって、作成された変数はすべてのスクリプトとその中で定義されている関数で使用できる、つまりグローバルであるとシステムに伝えます。

Octaveに対して、関数として構築したモデルを記述する必要があります。それをf_air関数とします。 当然、そのために別のファイルf_air.mを作成する必要があります。 自分でクランクしてみてください。 ヒントを示します。この関数の本体の最初で、グローバルな発射体パラメーターを再度決定する必要がありますが、すでに値はありません。 これは、関数がグローバル変数を見るために必要です。

 global c_f; global gamma; global d; 

非常に難しい場合は、ネタバレをご覧ください。



ここで、運動方程式系を解き、ballistics.mファイルでコマンドを与えます

 Y_air = lsode("f_air", Y0, t); plot(Y_air(:,1), Y_air(:,2)); 

つまり、空気抵抗を考慮せずに問題と同じ初期条件と同じ時間間隔で新しい運動方程式を統合し、軌道のグラフを描画します



うわー、最大飛行高度は非常に大幅に低下しました。 そして、47秒は射程距離が大きすぎるため、発射体はずっと早く地面に落ちます。 時間で遊ぼう



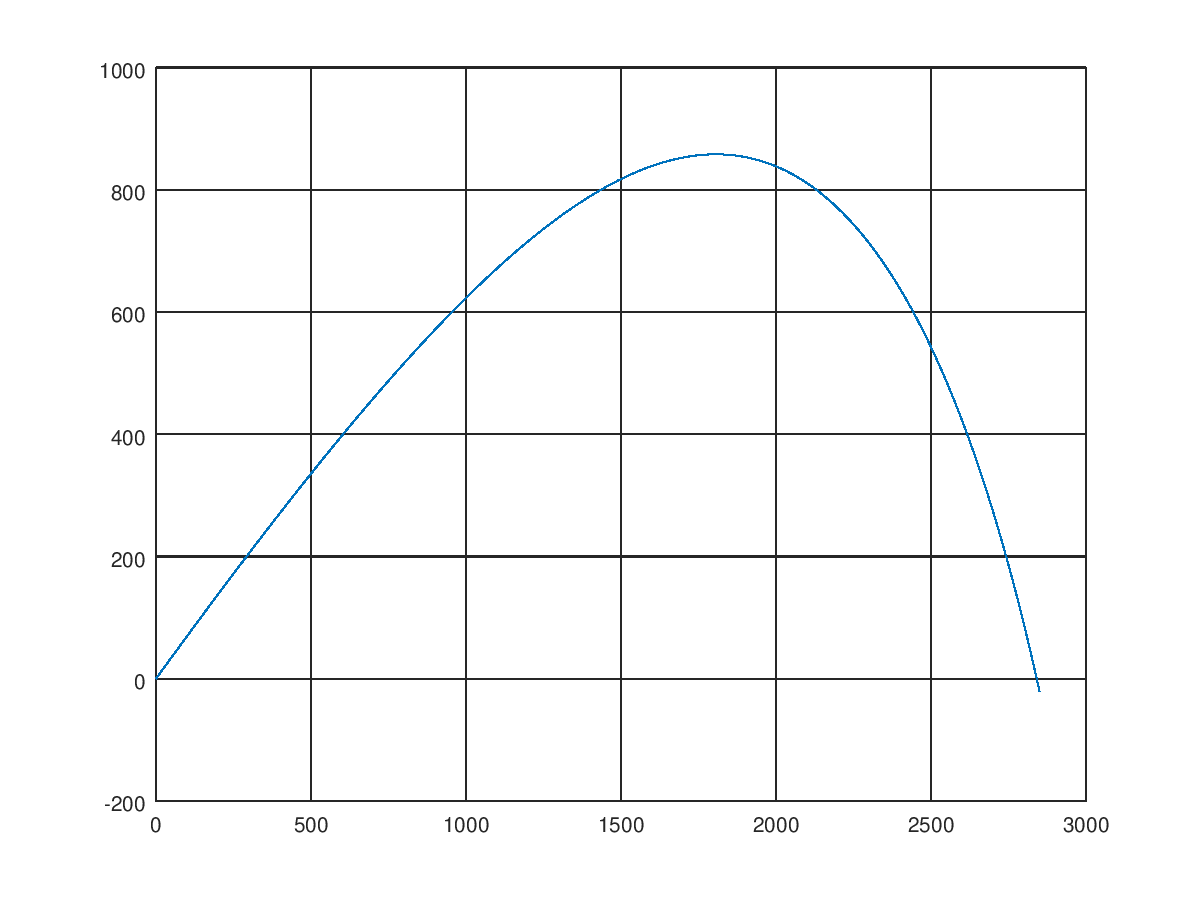
tend = 26秒では、飛行範囲が非常に重要であることがわかります。 空力抵抗が私たちの銃の特性に非常に大きく影響し、実際には無視できないことを見ることができます。 軌道の形状も変化します。上昇セクションではより緩やかで、下降セクションでは急降下し、理想的な放物線にあまり似ていません。

5.発射体の軌跡の比較

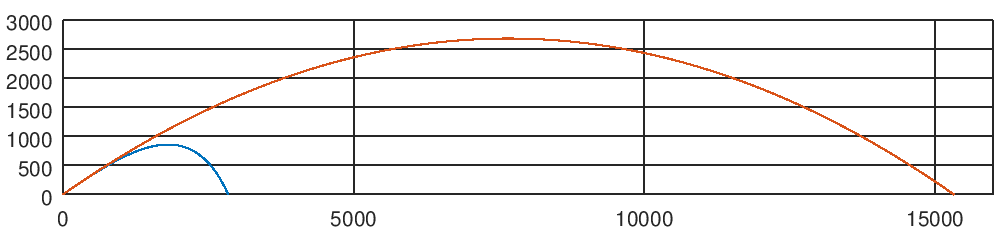
核の飛行をモデル化した結果が異なることはすでにわかりました。 しかし、すべては視覚的な比較で知られています。 2つの軌道を同時に構築します。 できますか はい、簡単です

 %    plot(Y_air(:,1), Y_air(:,2), Y(:,1), Y(:,2)); 

最初に、ある軌跡の横軸と縦座標を示し、次に別の軌跡を示しました。 どうしたの？



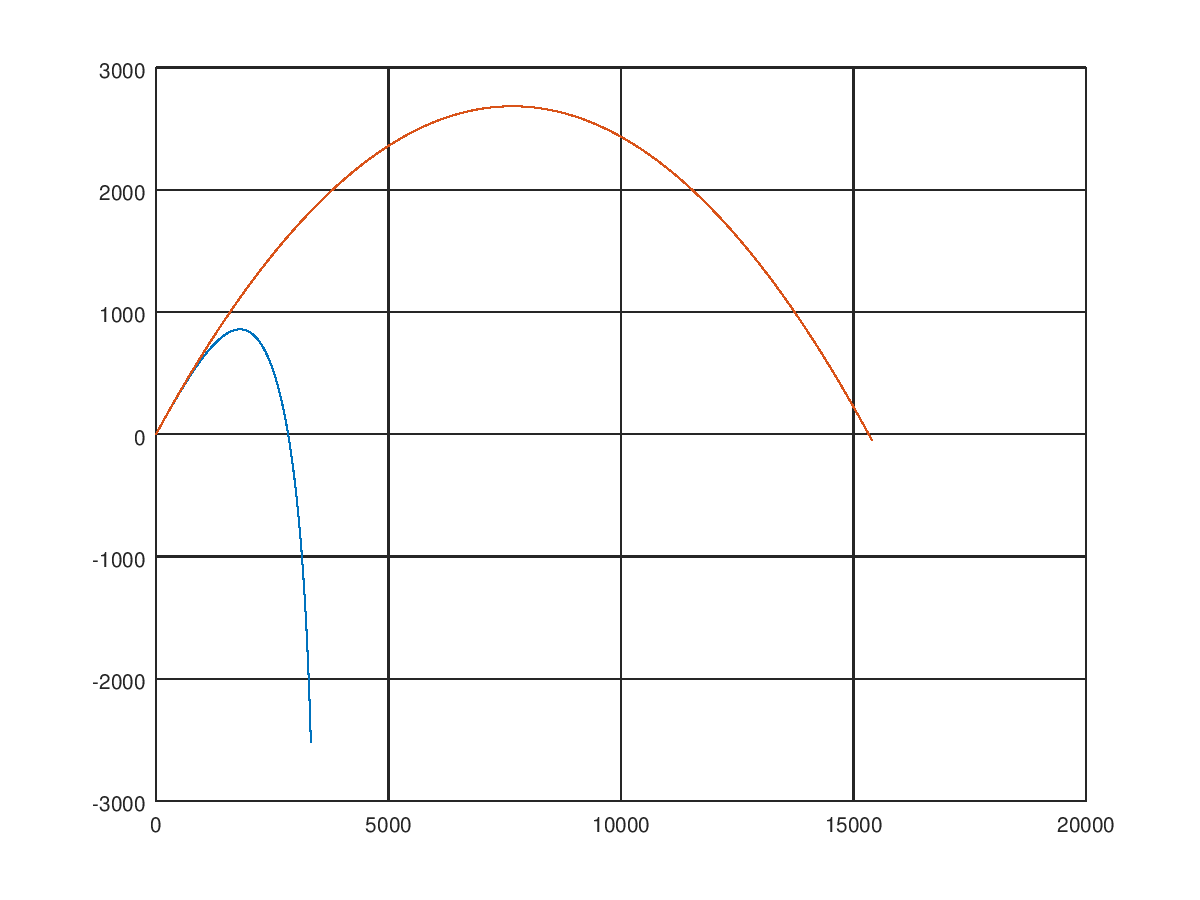
うーん、これはある種のナンセンスです。 そうです、異なるソリューションでの発射体の飛行時間は異なります。 モデル化していない表面とコアの衝突。 このような状況から抜け出すには、次のように、コマンド軸（）の軸に沿って座標を変更するための制限を設定します

 %        xmin = 0; xmax = 16000; ymin = 0; ymax = 3000; axis([xmin xmax ymin ymax], "manual"); 

これでチャートは次のようになります



すでに良い。 少なくとも軌跡を互いに比較できます。 そして、チャートのすべての軸を同じスケールにしたい場合は？ グーグルはそのようなコマンドを与えました

 set(gca,'dataaspectratio',[1 1 1]); 

すべての座標軸に沿ってグラフ軸の同じスケールを定義する



ネタバレの下、ballistics.mファイルの全文

おわりに

検討した例では、自然の法則の基本的な特性に直面しています-それらは非線形です。 空気抵抗を考慮すると、微分方程式の一部にある位相座標は非線形に入力されます。 この問題には分析的な解決策がありません。つまり、初等関数で表現されています。 技術の実際の問題に対する分析ソリューションの存在は、むしろ例外です。 そして、あなたはそれらを解決するときにモデリングなしで行うことはできません。

しかし、それ自体では、実際に運動方程式を解くことはほとんど意味がありません。 この決定は私たちに何を与えましたか？ はい、砲弾の飛行に対する空気抵抗の影響を見ました。 しかし、たとえば、私たちは多くの質問に答えませんでした。たとえば、私たちの銃の正確な射程距離はどれくらいですか？ 発射体の最大の高さは何ですか？ 最大範囲に到達するには、どの角度で撮影する必要がありますか？

数学モデルは、テクノロジーの実際的な問題を解決するために作成されます。 これが次回の話です。

PS：ドラフトの例がGithubで利用可能になります