
( ソース )
機械学習、特にニューラルネットワークの仕組みを他の人に伝えなければならないこともあります。 通常、勾配降下と線形回帰から始め、徐々に多層パーセプトロン、自動エンコーダー、畳み込みネットワークに移行します。 全員が頭をうなずきながらうなずきますが、ある時点で、抜け目のない人は必ず尋ねます:
そして、なぜ線形回帰の変数が独立していることがそれほど重要なのでしょうか?
または
また、通常の完全に接続されたネットワークではなく、画像に畳み込みネットワークが使用されるのはなぜですか?
「ああ、簡単です」と答えたいです。 -「変数が依存している場合、変数間の条件付き確率分布をモデル化する必要があるため」または「小さなローカルエリアでピクセルの共同分布を学習する方がはるかに簡単であるため」 しかし、ここに問題があります。生徒はまだ確率分布と確率変数について何も知らないので、他の方法で出て、より複雑に説明しますが、概念と用語は少なくなります。 また、バッチに関する正規化モデルまたは生成モデルについて説明するように求められた場合はどうすればよいかわかりません。
ですから、自分自身や他人を苦しめるのではなく、確率論の基本概念を覚えておいてください。
ランダム変数
年齢、身長、性別、子供の数が示されている人々のプロファイルがあると想像してください。
| 年齢 | 身長 | 性別 | 子どもたち |
|---|
| 32 | 175 | 1 | 2 |
| 28 | 180 | 1 | 1 |
| 17 | 164 | 0 | 0 |
| ... | ... | .... | .... |
このようなテーブルの各行はオブジェクトです。 各セルは、このオブジェクトを特徴付ける変数の値です。 たとえば、最初の人は32歳で、2人目の人は身長180 cmです。 しかし、すべてのオブジェクトに対して変数を一度に記述したい場合、つまり 列全体を取りますか? この場合、1つの特定の値ではなく、一度に複数の値があり、それぞれに固有の発生頻度があります。 可能な値のリスト+対応する確率は、 ランダム変数 (ランダム変数、rv)と呼ばれます。
離散および連続確率変数
これを頭に留めておくために、もう一度繰り返します。ランダム変数は、その値の確率分布によって完全に決定されます。 ランダム変数には、離散型と連続型の2つの主なタイプがあります。
離散変数は、明確に分離可能な値のセットを取ることができます。 通常、私はそれらを次のように描写します(確率質量関数、pmf):
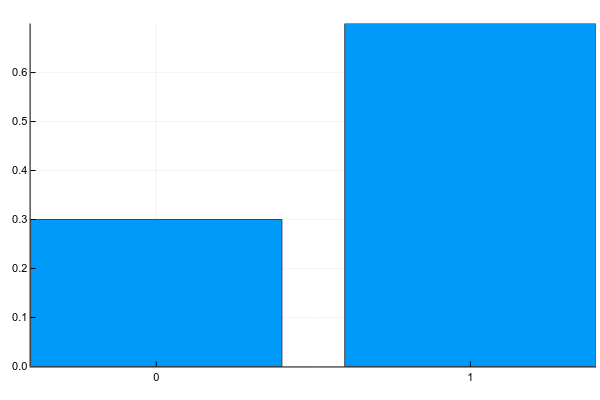
ジュリアコードPkg.add("Plots") using Plots plotly() plot(["0","1"], [0.3, 0.7], linetype=:bar, legend=false)
テキストでは、これは通常次のように書かれています(g-性別):
p(g=0)=0.3p(g=1)=0.7
つまり サンプルからランダムな人が女性になる確率( g=0 )は0.3で、男( g=1 )-0.7、これは女性の30%と男性の70%がサンプルに含まれていたという事実に相当します。
離散変数には、1人あたりの子供の数、テキスト内の単語の出現頻度、映画が視聴された回数などが含まれます。 ちなみに、有限数のクラスへの分類の結果も、離散確率変数です。
連続変数は、特定の間隔で任意の値を取ることができます。 たとえば、身長が175cmであると記録した場合でも、つまり 1センチメートルに丸めます。実際には175.8231 cmになります。 連続変数は通常、確率密度関数(pdf)曲線を使用して描かれます。

コード Pkg.add("Distributions") using Distributions xs = 140:0.1:200 ys = [pdf(Normal(172, 10), x) for x in xs] plot(xs, ys; xlabel="h", ylabel="p(h)", legend=false, show=true)
確率密度のグラフは注意が必要です:各列の高さがそのような値を得る確率を直接示す離散変数の確率質量のグラフとは異なり、確率密度は特定のポイント周辺の相対的な確率量を示します。 この場合、確率自体は区間についてのみ計算できます。 たとえば、この例では、サンプルから無作為に抽出された人の身長が160〜170 cmになる確率は約0.3です。
コード d = Normal(172, 10) prob = cdf(d, 170) - cdf(d, 160)
質問:ある時点での確率密度は1よりも大きくなりますか? もちろん、答えはイエスです。主なことは、グラフの下の総面積(または数学的に言えば、確率密度積分)が1に等しいことです。
連続変数のもう1つの難点は、その確率密度が常にうまく表現できるとは限らないことです。 離散変数の場合、値のテーブル->確率がありました。 連続の場合、これらは一般に無限の数の意味を持つため、機能しません。 したがって、彼らは通常、よく研究されたパラメトリック分布によってデータセットを近似しようとします。 たとえば、上のグラフはいわゆる例です。 正規分布。 その確率密度は次の式で与えられます。
p(x)= frac1 sqrt2 pi sigma2e− frac(x− mu)22 sigma2
どこで mu (mat。期待、平均)および \シグマ2 (分散)-分布パラメーター。 つまり 2つの数値しかないため、分布を完全に記述し、任意の点での確率密度または2つの値間の合計確率を計算できます。 残念ながら、どのデータセットからも遠く離れて、それを美しく表現できる分布があります。 これに対処するには多くの方法があります(少なくとも正規分布の混合を取ります)が、これは完全に異なるトピックです。
継続的分布の他の例:人の年齢、画像内のピクセルの強度、サーバーからの応答時間など。
共同分布、周辺分布、条件付き分布
通常、オブジェクトのプロパティは一度に1つではなく、他のプロパティと組み合わせて考慮されます。ここでは、いくつかの変数の共同分布の概念が表示されます。 2つの離散変数の場合、テーブルの形式でそれを表すことができます(g-性別、c-子の数):
| c = 0 | c = 1 | c = 2 |
|---|
| g = 0 | 0.1 | 0.1 | 0.1 |
| g = 1 | 0.2 | 0.4 | 0.1 |
この分布によると、データセットで2人の子供を持つ女性に会う確率は次のとおりです。 p(g=0、c=2)=0.1 と子供のない男- p(g=1、c=0)=0.2 。
たとえば、身長と年齢などの2つの連続変数の場合、再び分析分布関数を定義する必要があります p(h、a) それを概算し、
たとえば、 多次元法線 。 これをテーブルに書くことはできませんが、描くことができます:

コード d = MvNormal([172.0, 30.0], [10 0; 0 5]) xs = 160:0.1:180 ys = 22:1:38 zs = [pdf(d, [x, y]) for x in xs, y in ys] surface(zs)
共同分布がある場合、残りの変数を単純に合計(離散の場合)または積分(連続の場合)することで、各変数の分布を個別に見つけることができます。
p(g)= sumcp(g、c)p(h)= intp(a、h)da
これは、テーブルの各行または列の合計として表され、結果をテーブルのフィールドに入れることができます。
| c = 0 | c = 1 | c = 2 |
|---|
| g = 0 | 0.1 | 0.1 | 0.1 | 0.3 |
| g = 1 | 0.2 | 0.4 | 0.1 | 0.7 |
だから再び p(g=0)=0.3 そして p(g=1)=0.7 。 マージンプロセスは、結果の分布自体に名前を与えます-限界確率。
しかし、変数の1つの値がすでにわかっている場合はどうでしょうか? たとえば、目の前に男性がいて、その子供の数の確率分布を取得したいことがわかりますか? 共同確率表もここで役立ちます:前に男がいることを確実に知っているので、 g=1 、他のすべてのオプションを考慮から破棄し、1行のみを考慮することができます。
| c = 0 | c = 1 | c = 2 |
|---|
| g = 1 | 0.2 | 0.4 | 0.1 |
barp(c=0|g=1)=0.2 barp(c=1|g=1)=0.4 barp(c=2|g=1)=0.1
確率は何らかの方法で1つに合計する必要があるため、結果の値を正規化する必要があります。
p(c=0|g=1)=0.29p(c=1|g=1)=0.57p(c=2|g=1)=0.14
既知の値を持つ別の変数の分布は、条件付き確率と呼ばれます。
チェーンルール
そして、これらのすべての確率は、チェーンルールと呼ばれる1つの簡単な公式によって結び付けられています(チェーンルール、差別化においてチェーンルールと混同しないでください)。
p(x、y)=p(y|x)p(x)
この式は対称であるため、これも実行できます。
p(x、y)=p(x|y)p(y)
ルールの解釈は非常に簡単です:if p(x) -私が赤信号に行く確率、そして p(y|x) -赤信号に目を向ける人がヒットする確率、赤信号に移動してヒットする共同確率は、これら2つのイベントの確率の積に正確に等しくなります。 しかし、一般的に、緑になります。
従属変数と独立変数
すでに述べたように、共同分布表がある場合、システムに関するすべてを知っています。変数の限界確率を計算したり、ある変数を別の既知の変数で条件付きで分布したりできます。 残念ながら、実際には、このようなテーブルをコンパイルする(または連続分布のパラメーターを計算する)ことはできません。 たとえば、1000個の単語の出現の共同分布を計算する場合は、次の表が必要です。
107150860718626732094842504906000181056140481170553360744375038837035105112493612
249319837881569585812759467291755314682518714528569231404359845775746985748039345
677748242309854210746050623711418779541821530464749835819412673987675591655439460
77062914571196477686542167660429831652624386837205668069376
(1e301を少し超える)セル。 比較のために、観測可能な宇宙の原子数は約1e81です。 おそらく、追加のメモリバーを購入するだけでは十分ではありません。
ただし、詳細が1つあります。すべての変数が互いに依存しているわけではありません。 明日雨が降る確率は、私が道路を横断して赤信号になるかどうかにほとんど依存しません。 独立変数の場合、一方から他方への条件付き分布は単純に周辺分布です。
p(y|x)=p(y)
正直に言うと、1000語の結合確率は次のように記述されます。
p(w1、w2、...、w1000)=p(w1) timesp(w2|w1) timesp(w3|w1、w2) times... timesp(w1000|w1、w2、...)
しかし、単語が互いに独立していると「単純に」仮定すると、式は次のようになります。
p(w1、w2、...、w1000)=p(w1) timesp(w2) timesp(w3) times... timesp(w1000)
そして、確率を保つために p(wi) 1000ワードの場合、1000セルのみのテーブルが必要です。これはまったく問題ありません。
では、すべての変数を独立と見なさないのはなぜですか 残念ながら、大量の情報が失われます。 喉の痛みと発熱という2つの変数に応じて、患者がインフルエンザにかかる確率を計算したいとします。 それとは別に、喉の痛みは、病気と患者が大声で歌っているだけのことを示します。 温度が別に上昇している場合は、病気と、走りから戻ったばかりの事実の両方を示します。 しかし、体温とのどの痛みを同時に観察する場合、これは患者の病気休暇を処方する重大な理由です。
対数
文献では、確率だけでなくその対数が使用されることがよくあります。 なんで? すべてがかなり平凡です:
- 対数は単調に増加する関数です。 のために p(x1) そして p(x2) もし p(x1)>p(x2) それから logp(x1)> logp(x2) 。
- 積の対数は、対数の合計に等しくなります。 log(p(x1)p(x2))= logp(x1)+ logp(x2) 。
単語を含む例では、任意の単語に出会う確率 p(wi) 、原則として、統一よりもはるかに少ない。 計算精度が限られているコンピューターで多くの小さな確率を掛けようとすると、どうなるのでしょうか? ええ、私たちの確率はすぐにゼロに丸められます。 ただし、多数の個別の対数を追加すると 、計算の精度の限界を超えることは事実上不可能になります。
関数としての条件付き確率
これらのすべての例の後、特定の値が発生する回数をカウントすることで条件付き確率が常に計算されるという印象がある場合、私はこのエラーを払拭することを急いでいます:一般的な場合、条件付き確率は別のランダム変数の関数です:
p(y|x)=f(x)+\イプシロン
どこで \イプシロン -これはノイズです。 ノイズの種類-これは別のトピックでもありますが、ここでは取り上げませんが、機能については f(x) もっと詳しく見てみましょう。 上記の離散変数の例では、関数として単純な出現回数を使用しました。 これは、それ自体で多くの場合、たとえば、テキストまたはユーザーの振る舞いに対する単純なベイジアン分類器でうまく機能します。 もう少し複雑なモデルは線形回帰です:
p(y|x)=f(x)+ epsilon= theta0+ sumi thetaixi+ epsilon
ここでも、変数は xi 互いに独立しているが分布 p(y| mathbfx) パラメーターが線形関数を使用して既にモデル化されている mathbf theta 見つける必要があります。
多層パーセプトロンも機能ですが、すべての入力変数の影響を一度に受ける中間層のおかげで、MLPを使用すると、個々の変数だけでなく、入力の組み合わせに対する出力変数の依存性をシミュレートすることができます(喉と温度の例を思い出してください)。
畳み込みネットワークは、フィルターサイズでカバーされるローカルエリアのピクセル分布で動作します。 リカレントネットワークは、前のデータと入力データからの次の状態の条件付き分布と、現在の状態からの出力変数をモデル化します。 まあ、一般的に、あなたはアイデアを得る。
ベイズの定理と連続変数の乗算
ネットワークルールを覚えていますか?
p(x、y)=p(y|x)p(x)=p(x|y)p(y)
左側を削除すると、単純で明白な同等性が得られます。
p(y|x)p(x)=p(x|y)p(y)
そして、今転送する場合 p(x) 右に、有名なベイズの公式を取得します。
p(y|x)= fracp(x|y)p(y)p(x)
プロの発音興味深い事実:英語の「bayes」のロシア語の発音は「bias」という言葉のように聞こえます。 「オフセット」。 しかし、科学者「Bayes」の姓は「base」または「bayes」と読みます(Yandex Translateを聴く方が良いです)。
式は非常に打ち解かれているため、各部分には独自の名前が付いています。
- p(y) 事前配布(事前)と呼ばれます。 これは、特定のオブジェクト(たとえば、期限内にローンを支払った人の総数)を見る前からわかっていることです。
- p(x|y) 尤度と呼ばれます。 これは、そのようなオブジェクトを見る確率です(変数によって記述されます x )出力変数のこの値で y 。 たとえば、融資を行った人に2人の子供がいる可能性。
- p(x)= intp(x、y)dy -限界妥当性、一般的にそのようなオブジェクトを見る確率。 みんな同じです y 、したがって、ほとんどの場合考慮されず、ベイズの式の分子によって単純に最大化されます。
- p(y|x) -事後分布(事後)。 これは変数の確率分布です y オブジェクトを見た後。 たとえば、2人の子供を持つ人が期限内にローンを返済する可能性。
ベイジアン統計はとてつもなく興味深いものですが、これからは入りません。 私が触れたい唯一の質問は、連続変数の2つの分布の乗算です。これは、たとえば、ベイズ式の分子、および実際には連続変数の2番目の式すべてにあります。
2つの分布があるとしましょう p1(y) そして p2(y) :
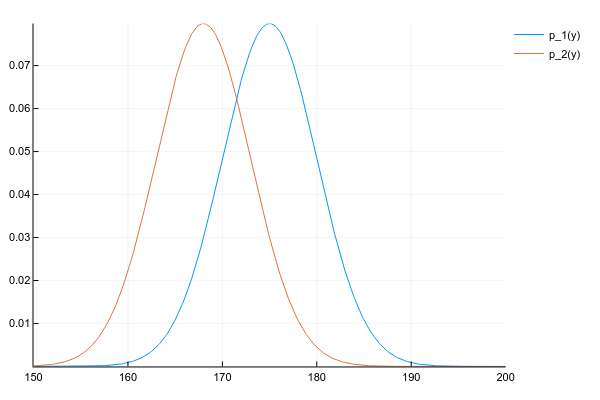
コード d1 = Normal(175, 5) d2 = Normal(168, 5) space = 150:0.1:200 y1 = [pdf(d1, y) for y in space] y2 = [pdf(d2, y) for y in space] plot(space, y1, label="p_1(y)") plot!(space, y2, label="p_2(y)")
そして、彼らの製品を入手したいのです。
p(y)=p1(y)p2(y)
各ポイントでの両方の分布の確率密度を知っているので、正直なところ、一般的な場合、各ポイントで密度を掛ける必要があります。 しかし、私たちがうまく行けば、 p1(y) そして p2(y) たとえば、2つの数値による正規分布(期待値と分散)のパラメーターを指定し、それらの製品の各ポイントでの確率を考慮する必要がありますか?
幸いなことに、多くの既知の分布の積は、簡単に計算可能なパラメーターを持つ別の既知の分布を与えます。 ここでのキーワードは、 共役事前です。
計算方法に関係なく、2つの正規分布の積により、もう1つの正規分布が得られます(正規化されていません)。
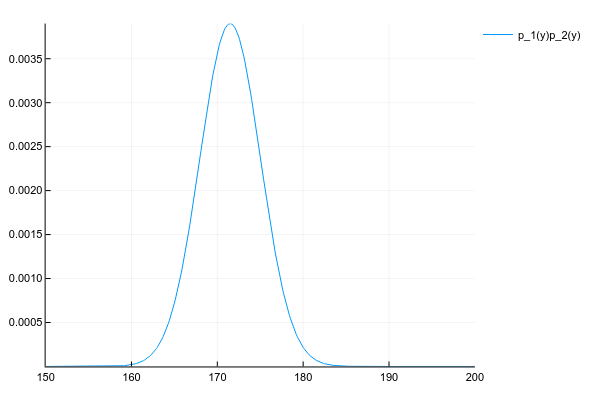
コード # # , plot(space, y1 .* y2, label="p_1(y)p_2(y)")
さて、比較のために、3つの正規分布の混合の分布:

コード plot(space, [pdf(Normal(130, 5), x) for x in space] .+ [pdf(Normal(150, 20), x) for x in space] .+ [pdf(Normal(190, 3), x) for x in space])
ご質問
これはチュートリアルであり、おそらく誰かがここに書かれた内容を思い出したいと思うでしょうから、ここに資料を修正するためのいくつかの質問があります。
人間の成長をパラメータを持つ正規分布のランダム変数とする mu=172 そして \シグマ2=10 。 身長178cmの人と出会う確率はどのくらいですか?
答え正解は、「0」、「無限に小さい」、または「定義されていない」と考えることができます。 そしてすべては、連続変数の確率が特定の間隔で考慮されるためです。 ポイントの場合、間隔はその幅であり、数学を学習した場所に応じて、ポイントの長さはゼロ、無限に小さい、またはまったく定義されていないと見なすことができます。
させる x -ローンの借り手である子供の数(3つの可能な値)、 y -人がローンを提供したかどうかのサイン(2つの可能な値)。 ベイズの公式を使用して、子供が1人いる特定の顧客がローンを提供するかどうかを予測します。 先験的分布と事後分布は、尤度と限界尤度と同様に、いくつの値を取ることができますか?
答えこの場合の2つの変数の共同分布の表は小さく、次のようになります。
| c = 0 | c = 1 | c = 2 |
|---|
| s = 0 | p(s = 0、c = 0) | p(s = 0、c = 1) | p(s = 0、c = 2) |
| s = 1 | p(s = 1、c = 0) | p(s = 1、c = 1) | p(s = 1、c = 2) |
どこで s -ローン成功のサイン。
この場合のベイズ式の形式は次のとおりです。
p(s|c)= fracp(c|s)p(s)p(c)
すべての値がわかっている場合:
- p(c) -これは、子供が1人いる人を見る限界確率であり、列の金額と見なされます c=1 そして単なる数字です。
- p(s) -私たちが何も知らないランダムに連れて行かれた人がローンを返還する先験的/限界確率。 テーブルの1行目と2行目の合計に対応する2つの値を持つことができます。
- p(c|s) -可能性、ローンの成功に応じた子供の数の条件付き分布。 これは子供の数の分布であるため、3つの可能な値があるはずですが、そうではありません:子供が1人いる人が来たことを確かに知っているため、テーブルの1列のみを考慮します。 しかし、ローンの成功は依然として問題であるため、2つのオプションが可能です-テーブルの2行。
- p(s|c) -事後分布、既知の場合 c しかし、2つの可能なオプションを検討してください s 。
2つの分布間の距離を最適化するニューラルネットワーク q(x) そして p(x) 多くの場合、最適化の目標としてクロスエントロピーまたはKullback-Leibler発散距離を使用します。 後者は次のように定義されます:
KL(q||p)= intq(x) log fracq(x)p(x)dx
intq(x)(。)dx -それは仲間です。 待っている q(x) 、そしてなぜ主な部分で- log fracq(x)p(x) -2つの関数の密度の差だけでなく、除算が使用されます q(x)−p(x) ?
答え log fracq(x)p(x)= logq(x)− logp(x)
言い換えれば、これは密度の差ですが、対数空間で計算がより安定しています。