チートシートが好きですか? 私たちは、量子コンピューティングに関するすべての最も重要な情報を収集する記事を崇拝し、今日公開します。 その前に出されたトピックに関する5つの記事から収集しました。 しかし、最も重要なことはチートシートのみであり、初心者向けのクイックガイドではありません。 初心者はすべての記事をまとめて勉強することをお勧めします。リンクはリストの下にあります!

サイクルからの記事:
- 量子コンピューティングと初心者向けQ#
- 量子コンピューティングの紹介
- 量子回路とゲート-入門コース
- 量子コンピューティングの基礎:純粋状態と混合状態
- Q#量子テレポーテーション
- 量子コンピューティング:リファレンス
ここでは、このシリーズの出版物にすでに掲載されている主要な状態、バルブ、マトリックス、有用な数式およびその他の情報に関する情報を見つけることができます。
目次
- フリーオーブ
- 基本的な量子状態
- ゲート、ダイ、および操作
- 有用な関係と方程式
フリーオーブ
ベクトルの任意のユニタリ変換|ψ〉は、ブロッホ球*に沿った点の単純な変位(|ψ〉としてマーク)として視覚化できます。 残念ながら、この視覚的表現は1キュービット状態にのみ適しています。マルチキュービットシステムの一般化はまだ発明されていません。 ブロッホ球体は、単位球体と呼ばれることもあります。
*純粋な状態は球の表面上の点に対応し、混合状態は球内の点に対応します。 詳細な説明については、「 量子コンピューティングの基礎:純粋状態と混合状態」を参照してください 。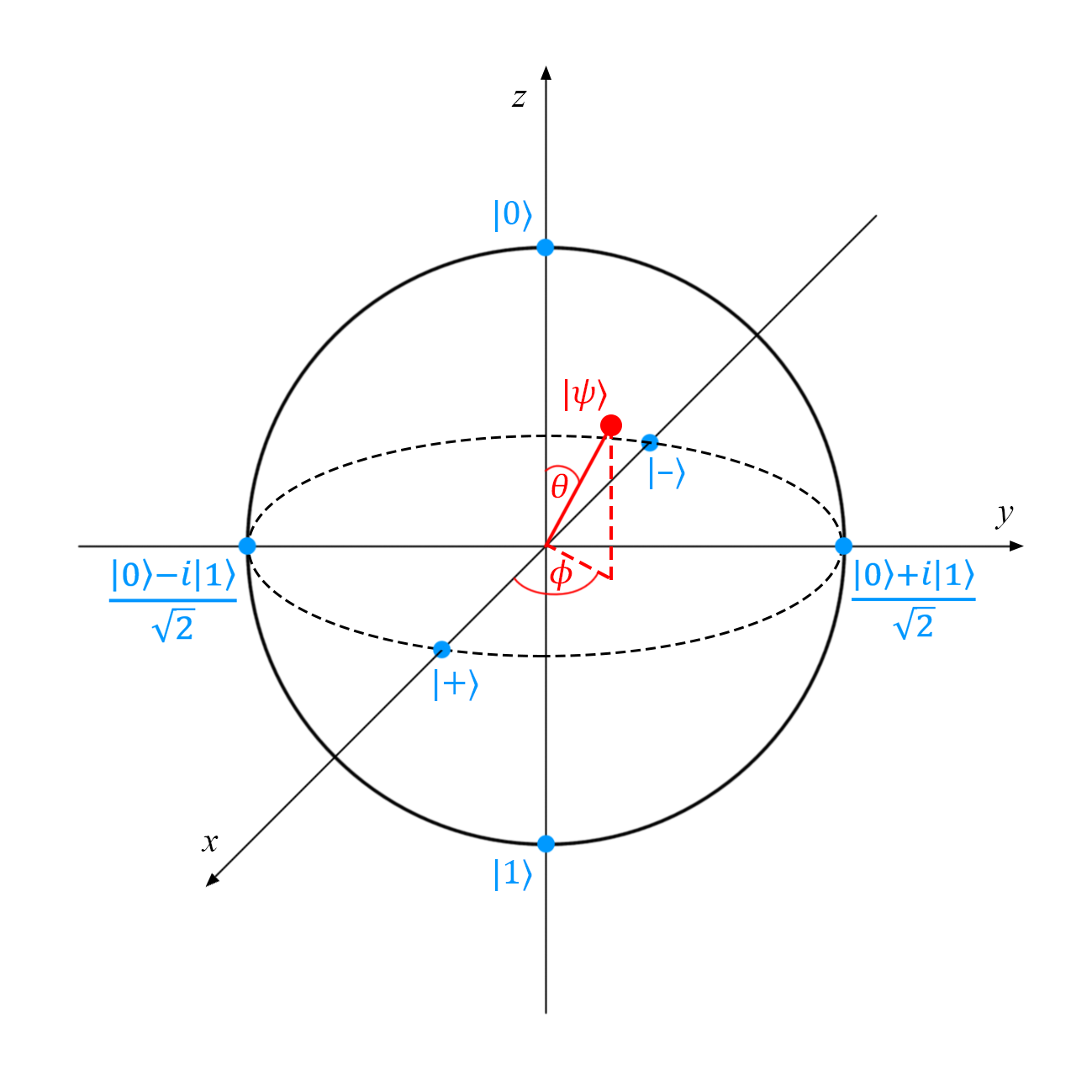
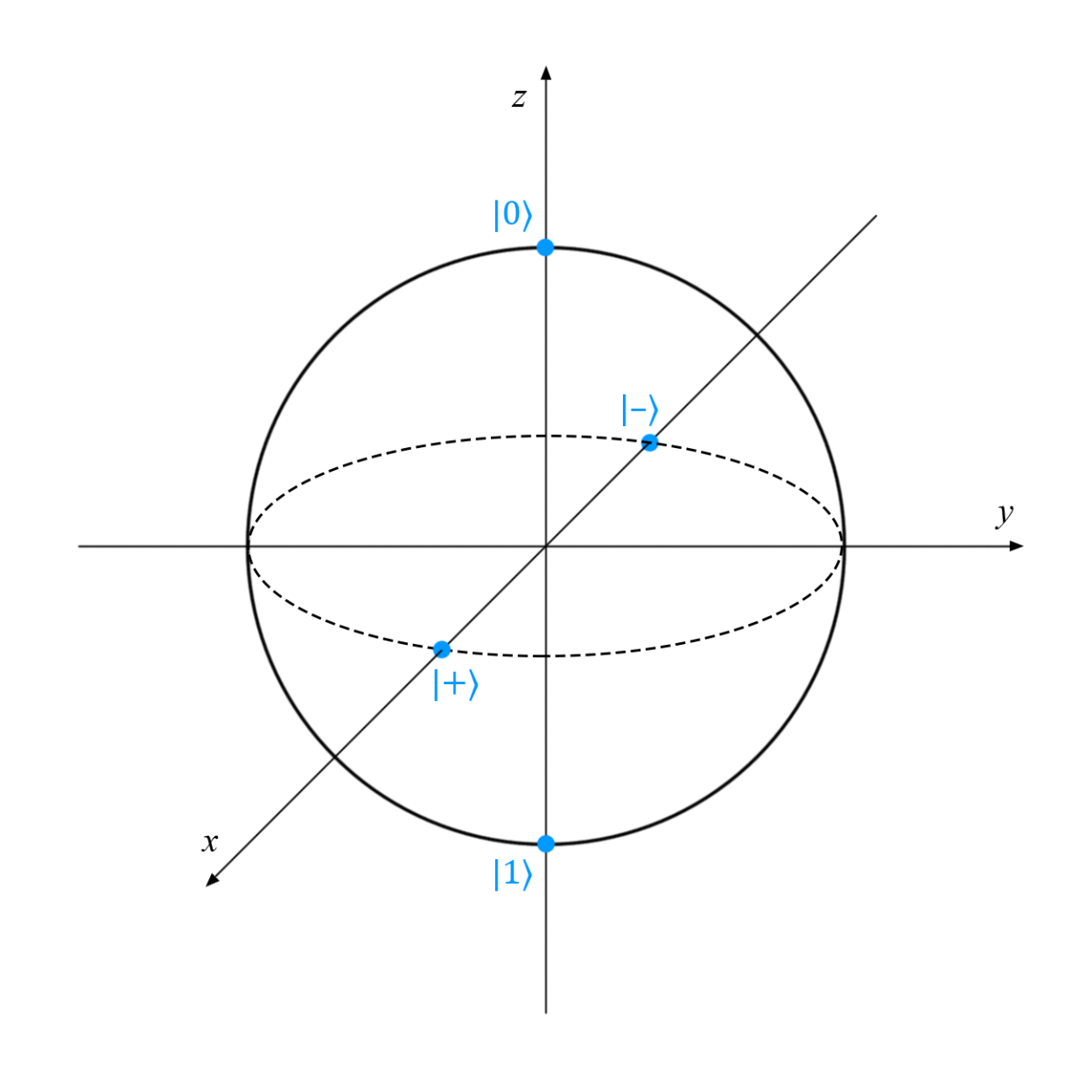
基本的な量子状態
単一キュービット条件
 ベル状態(EPRペア)は、2つのキュービットで構成される複雑なシステムの最も単純な例です。
ベル状態(EPRペア)は、2つのキュービットで構成される複雑なシステムの最も単純な例です。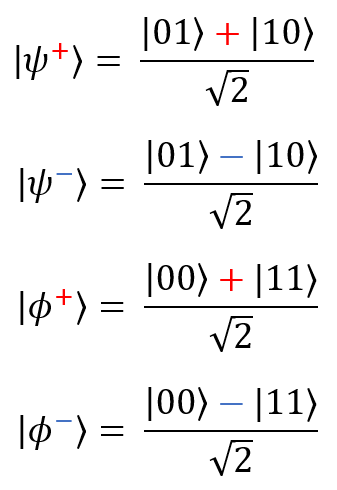 GHC(Greenberger – Horn – Zeilinger)は、一般的な形式(n量子ビット)と最も単純な形式(3量子ビット)で述べています。
GHC(Greenberger – Horn – Zeilinger)は、一般的な形式(n量子ビット)と最も単純な形式(3量子ビット)で述べています。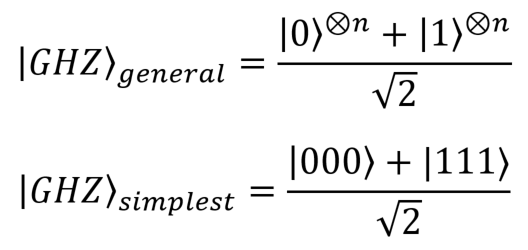
ゲート、ダイ、および操作
以下は、
バルブと回路に関する以前の
出版物で発表された最も重要なバルブの要約です。 すべての1キュービットゲートと2キュービットゲートの操作に関する情報を追加しました(3つ以上の操作がある場合、式が長くなりすぎます)。 制御されたゲートの式で
は、以前の出版物の1つと同様に、アイデンティティマトリックス(II)が赤で強調表示され、元のゲートのマトリックスが青で強調表示されます。
有用な関係と方程式
行列パウリ
パウリ行列は、それ自体の逆行列です。
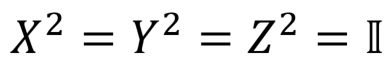
密度演算子
密度演算子は次のように定義できます
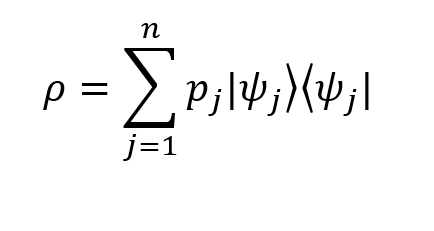
ここに:
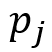 -最初の瞬間にシステムが状態にある確率
-最初の瞬間にシステムが状態にある確率 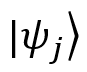 。
。- アイテム
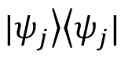 ベクトルの外部積の結果に対応
ベクトルの外部積の結果に対応 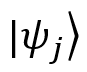 それ自体(このような変換は設計演算子とも呼ばれます)。
それ自体(このような変換は設計演算子とも呼ばれます)。 - nは、システムの可能な状態の総数です(この例では3つあります)。
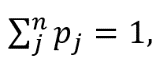 予想どおり(すべての可能な状態の確率の合計は1です)。
予想どおり(すべての可能な状態の確率の合計は1です)。
資源