あなたが私の家に入るとき...えーと...私の妻と私は家で私たちの仕事にも関連する芸術作品を持ちたいと思っていました。 そのため、2つのことがわかります。そのうちの1つはドラゴンカーブです。これについては後で詳しく説明します。 そしてもう一つはこの作品です。 これは、Pete HainによるRoad to Wisdomからの行です。

しなければならない
知恵へ
永遠に届く
私たちに何を
とても魅力的
うるさい
また
そしてまた、
そしてまた
間違える
しかし、それほど頻繁ではありません
あまり頻繁に
あまり頻繁ではありません。
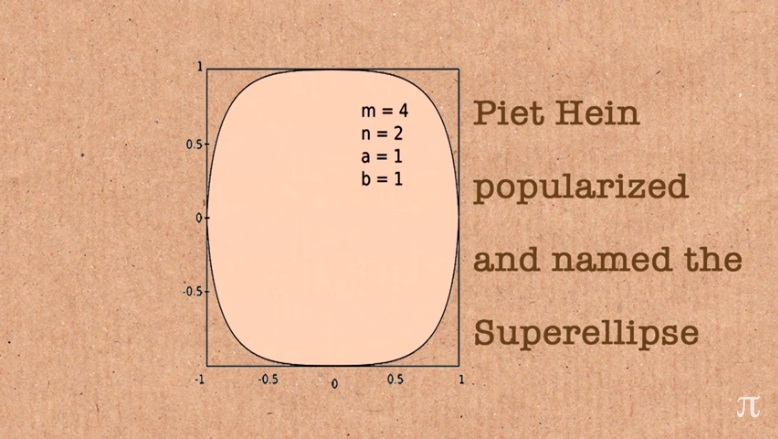
これは私のお気に入りのフレーズの1つです。 私の人生のある種の話は、間違いを犯し、そこから何かを学ぼうとしています。 このフレーズは、スーパー楕円の形で設計されました。これは、ピートハインの素晴らしい発見の1つです。 この楕円はより完全で、多くの建築製品で使用されています。
ドラゴンカーブのアイデアは何ですか? これが、1960年代後半の数人の物理学者のおかげで生まれたものです。

一枚の紙を取り、曲げ、何度も何度も曲げて、n回繰り返します。 左の壁にドラゴンカーブがある場合、Nは9です。

これを見ると、いくつかの折り目が内側に曲がっているのがわかります。 この曲線に沿って移動していると想像した場合、ここで左に曲がり、次にここで左に曲がり、ここで左に曲がりますが、右に曲がってから右に曲がり、再び左に曲がります。

これは、左右で構成されるパターンです。 最も驚くべきことは、この曲線を続けて9回行い、90度の角度でこれらすべてのベンドを開くと、スペースを埋め始め、美しい実用的なパターンを作成するトラックが得られることです。 たとえば、このタイルから始めましょう。

カメラを少し近づけると、妻と私がここに名前を書いたことがわかりますが、この話については後で話しましょう。 この曲線が始まり、左に曲がり、再び左に曲がり、次に右に曲がり、次に左に曲がり、左に曲がります。 これはまさに、紙を折るときに得られるパターンです。 シートを9回折りたたんでいるため、壁には512のステップが表示されています。 おそらく511です。曲線はここで終了して続行しますが、途中で非常に混乱します。
オタクアートの観点からすれば、素晴らしいのは、3種類のタイルしか必要ないということです。

完全に空のタイル、またはこのようにループが1つしかないタイル、またはこのように2つのループがあるタイルが必要です。 そして、もちろん、2つのループのあるタイルを、この方向に向けることができます。 その後、ここでは接続しませんが、ここでは孤立した円を形成します。

必要な空のタイルの数、1つのループを持つタイルの数などを計算する必要がありました。 紙と厚紙のブレッドボードモデルを作成し、家の設計中に住んでいたアパートに保管しました。 そして、私たちはそれがクールなデザインであり、最終的に建てられたときに私たちの家にこのようなものを置くことがクールだと決めました。

私たちは両方とも、カリフォルニア州サウサリートにあるHIT Ceramicsのタイルが好きで、デザインのモックアップがあったので、セラミックを見て、そこで働いている人々と話をしました。 そして、一定の数の空のタイル、1つのループを持つタイルなどを注文できるかどうか疑問に思っていました。 はい、できると答えましたが、3.5インチの正方形のタイルを作ります。
そして、私の設計では、2インチの正方形が必要でした。 9から8に変更しても、計算を変更することはできませんでした。同じ興味深いパターンになりますが、同時に巨大で、そのようなスケールでは正常に見えません。
この種のパターンは、そのサイズでは非常に魅力的であり、大きなサイズではありません。 私たちは話をしていた人が、この素晴らしいアイデアでこのように旅して以来、私たちが動揺しているのを見たので、非常に動揺して失望したようです。 そして彼は言った:「ちょっと待って、6月に休暇を取り、工場を閉鎖しているが、ここには警備員がいる。
あなたが来て私たちの機器を使用することができます、私たちはあなたに私たちの粘土を使用してタイルを作らせます。 2x2インチのサイズにカットする場合は、アイシングでタイルを覆い、タイルを焼き付けます。 でした。 私たちはそこに行き、そこで一日中過ごし、いくつかの予備のタイルを含むこのタイルをすべて作りました。 そして、このタイルの開始点にイニシャルを配置しました。 その後、このタイルが解雇されました。 火からのいくつかの跡がまだ時々見えることがあります、いくつかの場所のタイルは、発射中に少し割れました。

まだ9がありました。8つのステップの後、ラインはここにあり、16の後、ステップ32にあります。
数年が経ち、私はついに私の本「Fun and Games」に章についての章を投稿しました。 そして、私はこのトピックに関するすべての記事を読み、ドラゴンカーブについて書いたところ、この*壁を指す*が間違っているという衝撃的な発見に至りました。

この曲線は9倍になっていますが、9倍を間違った方向に折りました。 このようにする代わりに、私は他の方法で行った。
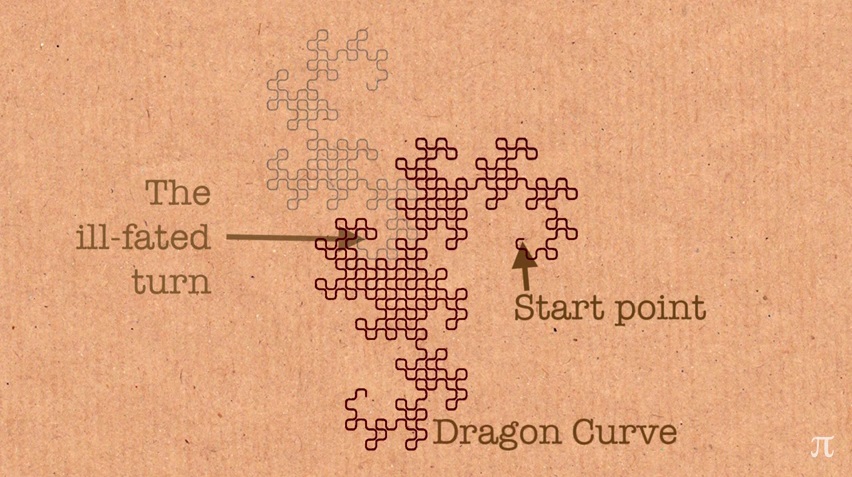
この曲線の後半には、実際には異なる折り目があります。 数学の観点から、私はこの曲線で30年間生きましたが、設計に数学的な誤りがあることに気づきませんでした。
-これについてどう思いますか?
-フレーズの意味を感じました:
知恵へ
永遠に届く
私たちに何を
とても魅力的
うるさい
また
そしてまた、
そしてまた
間違える
しかし、それほど頻繁ではありません
あまり頻繁に
あまり頻繁ではありません。
GoTo Schoolについて