GoogleのS2 Geoライブラリと導入事例の紹介

こんにちは、Habr！

私の名前はマルコです。プラットフォームチームのBadooで働いています。 少し前のGopherCon Russia 2018で 、座標の操作方法について話しました。 ビデオを見るのが嫌いな人（そしてもちろん興味のある人）のために、レポートのテキスト版を公開しています。

はじめに

現在、世界中のほとんどの人は、常時インターネットにアクセスできるスマートフォンを持っています。 数字で言えば、2018年には約50億人がスマートフォンを使用し 、そのうち60％がモバイルインターネットを使用します。

これらは膨大な数です。 企業がユーザー座標を取得することは簡単になりました。 これらの使いやすさとアクセシビリティは、座標に基づいて膨大な数のサービスを生み出しました（そして生み出し続けています）。

IngressやPokemon Goなど、世界を征服したUberのような企業を知っています。 しかし、銀行のアプリケーションでは、近くにATMや割引を見る機会があります。

Badooでは、座標を非常に積極的に使用して、ユーザーに最適で関連性の高い興味深いサービスを提供しています。 しかし、どのような用途について話しているのでしょうか？ 私たちが持っているサービスの例を見てみましょう。

Badooのジオサービス

最初の例：MeetmakerとGeousers

Badooは主にデートです。 人々がお互いを知り合う場所。 人を検索する際の重要な基準の1つは、距離です。 実際、ほとんどの場合、モスクワの少女は、遠く離れたウラジオストックではなく、少なくともモスクワに住んでいるか、少なくともモスクワに住んでいる少年に会いたい。



「はい」または「いいえ」で「再生」またはユーザーを案内するユーザーを選択し、特定の半径内であなたに合った基準を持つユーザーを検索するサービス。

2番目の例：Geoborder

ユーザーがどの都市にいるのか、どの国にいるのか、より正確には、たとえばどの空港に、どの大学にあるのかという質問に答えるために、いわゆるジオフェンシングを扱うジオボーダーサービスを使用します。



これらの質問に答える最も簡単な方法は、ユーザーから市内中心部または大学の中心までの距離を考慮することですが、このアプローチは非常に不正確であり、多数の境界条件に依存します。

そのため、国、都市、重要なオブジェクト（たとえば、私が話した大学や空港など）の非常に正確な境界線を描きました。 これらの境界はポリゴンによって設定されます。 このような境界のセットがあると、ユーザーがポリゴンの内側にいるかどうか、またはポリゴンに最も近いポリゴンを見つけることができます。 したがって、どの都市にあるかを言うことも、最も近い都市を見つけることもできます。

3番目の例：Bumpd

Bumped Intoと呼ばれる非常に人気のある機能があります。これは、バックグラウンドで時間と空間で交差するユーザーを常に検索し、この男の子またはこの女の子と同じ場所に定期的にアクセスすることを示します。定期的に同じ道を進みます。 この機能は、会話を開始できるトピックに精通するもう1つの理由であるため、ユーザーに非常に人気があります。

4番目の例：Geocache-「取得」するのに費用がかかる地理情報のキャッシュ

さて、私が言及する最後の例は、地理情報のキャッシングに関連しています。 たとえば、Booking.comのデータを使用すると、周りのホテルに関する情報が提供されますが、毎回Booking.comにアクセスするには長すぎます。 このパイプの穴のように、あなたのインターネットパイプはおそらくかなり狭いでしょう。 おそらく、データのためにアクセスするサービスは、リクエストごとにお金がかかるので、少し節約したいでしょう。



この場合、キャッシングレイヤーがあると便利です。キャッシングレイヤーは、低速または高価なサービスのリクエスト数を大幅に削減し、外部に非常に類似したAPIを提供します。 このエリアのすべてまたはほとんどのホテルについて彼がすでに知っていることを理解するサービス。このデータは比較的新しく、したがって、外部サービスでそれに入ることはできません。 このようなタスクは、Geocacheと呼ばれるサービスによって解決されます。

ジオサービスの機能

多くの座標があり、座標が重要であり、それらに基づいて多くの興味深いサービスを作成できることをすでに認識しています。 それでは、次は何ですか？ 実際、問題は何ですか？ 座標は、ユーザーから受け取った他の情報とどのように異なりますか？

そして、2つの機能があります。



まず、地理データは3次元、または2次元です。これは、一般的な場合、高さに関心がないためです。 これらは緯度と経度で構成され、ほとんどの場合、両方で同時に検索が行われます。 エリアで検索を想像してください。 一般的なDBMSの標準インデックスは、このような使用には最適ではありません。



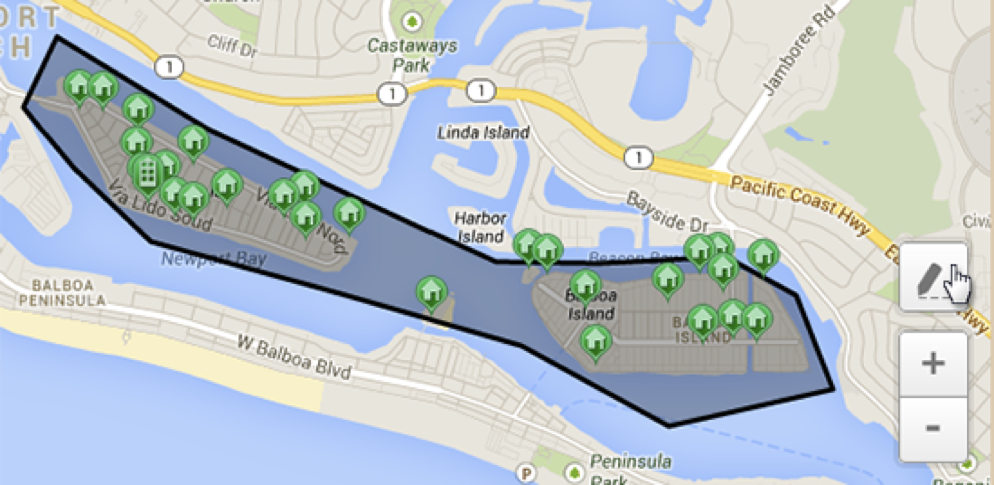
第二に、多くのタスクには、ポリゴンなどのより複雑なデータタイプが必要です。これについては、BadooのGeoborderサービスの例で説明しました。 もちろん、ポリゴンは頂点座標で構成されますが、追加の処理が必要であり、これらのタイプのデータに対する検索クエリも複雑です。 クエリ「ポイントに最も近いポリゴンを検​​索する」または「特定のポイントを含むポリゴンを検​​索する」をすでに見てきました。

サービスを書く理由

これらの機能に準拠するために、多くのDBMSには、多次元データ用にシャープ化された特別なインデックス 、およびポリゴンやポリラインなどのオブジェクトを操作できる追加機能が含まれています。



おそらく最も顕著な例はPostGISです 。これは、一般的なPostgreSQL DBMSの拡張機能であり、座標と地理を操作するための最も広い可能性を持っています。

ただし、既製のDBMSを使用することが唯一のソリューションではなく、常に最良のソリューションではありません。



サービスとDBMSとの間でサービスのビジネスロジックを共有したくない場合、DBMSで利用できないものが必要な場合、サービスを完全に管理したい場合、DBMSをスケーリングする機能に制限されない場合は、サービスに地理データを検索および操作する機能を組み込みたい。

このアプローチは間違いなく柔軟性がありますが、DBMSはオールインワンソリューションであり、レプリケーションなどの多くのインフラストラクチャが既に行われているため、はるかに複雑になる可能性があります。 レプリケーション、そして実際には、座標を操作するためのアルゴリズムとインデックス。

しかし、すべてがそれほど怖いわけではありません。 必要なもののほとんどを実装するライブラリを紹介したいと思います。 これは一種の立方体で、球体のジオメトリを操作したり、座標で検索したりする必要がある場所に簡単に組み込まれます。 S2というライブラリを使用します。

S2

S2は、ジオメトリ（球体を含む）を操作するためのライブラリであり、ジオインデックスを作成するための非常に便利な機能を提供します。

最近まで、S2はほとんど知られておらず、ドキュメントも非常に貧弱でしたが、Googleはオープンソースで「 再リリース 」することを決定し、製品のサポートと開発を約束してレイアウトに追加しました。

ライブラリのメインバージョンはC ++で記述されており、Goバージョンを含む他の言語の公式ポートまたはバージョンがいくつかあります。 現在、GoバージョンはC ++バージョンのすべてを100％実装しているわけではありませんが、ほとんどのものを実装するには十分です。

Googleに加えて、このライブラリはFoursquare 、 Uber 、 Yelp 、そしてもちろんBadooなどの企業でも積極的に使用されています。 また、ライブラリを内部で使用する製品の中で、よく知られているMongoDBをすべてのユーザーにアピールできます。

しかし、これまでのところ、S2が便利な理由と、ジオサーチを使用してサービスを簡単に作成できる理由について実用的なことは何も言いませんでした。 2つの例を見る前に、自分自身を修正し、内部を少し掘り下げてみましょう。

投影

通常、地理学では、平面上で最も一般的な地球の投影の1つを使用します。 たとえば、 メルカトル図法はすべて知っています。 このアプローチの欠点は、投影に何らかの形で歪みがあることです。 私たちの地球は飛行機にあまり似ていません。



ロシアとアフリカを比較した有名な写真を思い出してください。 ロシアは地図上では巨大ですが、実際、アフリカの面積はすでにロシアの面積の2倍です！ これはメルカトル図法の歪みの例にすぎません。



S2は、球面投影と球面ジオメトリのみを使用してこの問題を解決します。 もちろん、地球も完全な球体ではありませんが、球体の場合の歪みはほとんどのタスクで無視できます。

単一球または単位球 、つまり半径1の球で作業し、 中心角 、球形の長方形、 球形のセグメントなどの概念を使用します 。

S2という名前は、単位球を示す数学表記に由来しています。

しかし、ほとんどすべての数学が図書館に引き継がれているので、怖がってはいけません。

階層セル

ライブラリの2番目の（そして最も重要な）機能は、グローブをセル（英語-セル）に階層的に分割するという概念です。


パーティションは階層的です。つまり、セルのレベル（またはレベル）などがあります。 そして、あるレベルでは、セルはほぼ同じサイズです。

セルは地球上の任意のポイントを設定できます。 幅が1センチメートル未満のサイズの最大30レベルのセルを使用すると、ご存じのように精度が非常に高くなります。 下位レベルのセルは同じポイントを設定できますが、精度はすでに低くなります。 たとえば、5 m x 5 m。



セルは、ポイントだけでなく、ポリゴンや一部の領域などのより複雑なオブジェクトも指定できます（写真では、たとえばハワイが表示されています）。 この場合、そのような数値はセルのセット（おそらく異なるレベル）によって定義されます。


このようなパーティションは非常にコンパクトです。各セルは1つの64ビット数でエンコードできます。

ヒルベルト曲線

セルには単一の64ビット数が与えられると述べました。 ここにある！ 地球上の座標またはポイントは、デフォルトでは2つの座標で設定されますが、標準の方法で作業するには不便であるため、1つの数値で指定できます。 しかし、これを達成する方法は？ 見てみましょう...

球体の階層パーティションはどのように発生しますか？



最初に球体を立方体で囲み、6つの面すべてに投影し、その場で投影を微調整して歪みを除去します。 これはレベル0です。次に、立方体の6つの面のそれぞれを4つの等しい部分に分割できます-これはレベル1です。また、結果の4つの部分はそれぞれ4つの等しい部分-レベル2に分割できます。



しかし、この段階では、まだ二次元性があります。 そして、ここで遠い過去からの数学的アイデアが救いに来ます。 19世紀の終わりに、David Hilbertは、回転、折り畳み、したがって空間を埋める1次元の線で空間を埋める方法を思いつきました。 ヒルベルト曲線は再帰的であるため、精度または密度を選択できます。 必要に応じて、小さなピースをより密に充填できます。



このような曲線で2次元空間を埋めることができます。 そして今、この曲線を取り、それを直線に引き伸ばすと（文字列を引っ張っているように）、多次元オブジェクトを記述する1次元のオブジェクトを取得します-この線上の1次元のオブジェクトまたは座標は、便利で扱いやすいです。

中央レベルの1つでの地球のヒルベルト曲線の塗りつぶしは、次のようになります。



ヒルベルト曲線のもう1つの特徴は、曲線の近くにあるポイントが近くにあり、空間にあるという事実です。 その逆は常にではありませんが、基本的には真実です。 また、この機能は積極的に適用されます。

64ビット変数へのエンコード

しかし、なぜ、セルIDと呼ばれる単一の64ビット数でセルをエンコードできるのでしょうか？ 見てみましょう。

立方体の6つの面があります。 6つの異なる値を3ビットでエンコードできます。 対数を覚えておいてください。

次に、6つの面のそれぞれを30回4つの等しい部分に分割します。 各レベルでセルを分割する4つの部分の1つを設定するには、2ビットで十分です。



合計3 + 2 * 30 =63。そして、セルがCellIDによって与えられるレベルを知り、素早く理解するために、最後に1ビットを追加します。



これらすべてのパーティションと1つの数値でのヒルベルト曲線のコーディングは何をもたらすのでしょうか？

1. 地球上の任意のポイントを1つのCellIDでエンコードできます。 レベルに応じて、異なる精度が得られます。
2. 地球上の任意の2次元オブジェクト、1つ以上のCellIDをエンコードできます。 同様に、レベルを変えることで正確に遊ぶことができます。
3. ヒルベルト曲線のプロパティは、その隣にあるポイントが近くにあり、空間にあること、およびCellIDが単なる数字であるという事実により、Bツリータイプの通常のツリーを検索に使用できます。 探しているもの（ポイントまたはリージョン）に応じて、getまたはrangeスキャン、つまり、toとfromの検索を使用します。
4. 地球をレベルに分割すると、システムをシャーディングするためのシンプルなフレームワークが得られます。 たとえば、ゼロレベルでは、サービスを最初のレベル（24など）で6つのインスタンスに分割できます。

ここで、この理論的知識を統合するために、2つの例を見てみましょう。 2つの簡単なサービスを作成しますが、最初のサービスは検索のみです。

例

私たちは周りの人を見つけるためのサービスを書きます

検索インデックスを作成します。 インデックスを作成する関数、インデックスに人を追加する関数、そして実際には検索関数が必要です。 さて、テスト。

type Index struct {} func NewIndex(storageLevel int) *Index {} func (i *Index) AddUser(userID uint32, lon, lat float64) error {} func (i *Index) Search(lon, lat float64, radius uint32) ([]uint32, error) {} func TestSearch(t *testing.T) {} 

ユーザーはIDと座標によって設定され、検索は検索センターの座標と検索半径によって設定されます。

インデックスでは、 Bツリーが必要です。ノードのstorageLevelレベルのセルと、このセルのユーザーのリストを格納します。 storageLevelセルレベルは、初期検索の精度とパフォーマンスの間の選択です。 この例では、1 kmあたり約1 kmのセルサイズを使用します。 Less関数は、Bツリーが機能するために必要です。そのため、ツリーは、どの値が小さいか、大きいかをツリーが理解できます。

 type Index struct { storageLevel int bt *btree.BTree } type userList struct { cellID s2.CellID list []uint32 } func (ul userList) Less(than btree.Item) bool { return uint64(ul.cellID) < uint64(than.(userList).cellID) } 

次に、ユーザーの追加機能を見てみましょう。

 func (i *Index) AddUser(userID uint32, lon, lat float64) error { latlng := s2.LatLngFromDegrees(lat, lon) cellID := s2.CellIDFromLatLng(latlng) cellIDOnStorageLevel := cellID.Parent(i.storageLevel) // ... } 

ここでは、最初にS2の動作を確認します。 度で指定された座標をラジアンに変換してから、最大30レベル（つまり、最小セルサイズ）のこれらの座標に対応するCellIDに変換し、結果のCellIDをレベルのCellIDに変換します。人々を保ちます。 この関数の「内側」を見ると、数ビットがゼロになるだけです。 CellIDのエンコード方法を覚えておいてください。

 func (i *Index) AddUser(userID uint32, lon, lat float64) error { // ... ul := userList{cellID: cellIDOnStorageLevel, list: nil} item := i.bt.Get(ul) if item != nil { ul = item.(userList) } ul.list = append(ul.list, userID) i.bt.ReplaceOrInsert(ul) return nil } 

次に、このユーザーをBツリーの適切なセルに追加するだけです。 または、誰かが既にそこにいる場合は、最初に、またはリストの最後に。 簡単なインデックスの準備ができました。

検索機能に移動します。 最初の変換は似ていますが、セルではなく、座標でポイントオブジェクトを取得します。 これが検索の中心です。

 func (i *Index) Search(lon, lat float64, radius uint32) ([]uint32, error) { latlng := s2.LatLngFromDegrees(lat, lon) centerPoint := s2.PointFromLatLng(latlng) centerAngle := float64(radius) / EarthRadiusM cap := s2.CapFromCenterAngle(centerPoint, s1.Angle(centerAngle)) // ... return result, nil } 

さらにメートル単位の半径に沿って、中心角を取得します。 これは、球の中心から来る角度です。 この場合の変換は単純です。メートル単位の地球の半径をメートル単位の地球の半径で割れば十分です。



検索の中心点と取得した角度によって、球形のセグメント（または「帽子」）を計算できます。 実際、これは球上の円ですが、3次元のみです。



さて、内部に見る必要がある「帽子」があります。 しかし、どのように？ これを行うには、S2に、サークルまたは「キャップ」を完全にカバーするstorageLevelレベルのセルのリストを提供するように依頼します。

 func (i *Index) Search(lon, lat float64, radius uint32) ([]uint32, error) { // ... rc := s2.RegionCoverer{MaxLevel: i.storageLevel, MinLevel: i.storageLevel} cu := rc.Covering(cap) // ... return result, nil } 

次のようになります。



受信したセルを通過し、Bツリーでget-sして、内部にいるすべてのユーザーを取得するだけです。

 func (i *Index) Search(lon, lat float64, radius uint32) ([]uint32, error) { // ... var result []uint32 for _, cellID := range cu { item := i.bt.Get(userList{cellID: cellID}) if item != nil { result = append(result, item.(userList).list...) } } return result, nil } 

テストのために、インデックスと複数のユーザーを作成します。 3近い、2つ離れています。 また、半径が小さい場合は3人のユーザーのみが戻り、半径が大きい場合はそれだけであることを確認します。 やった！ 私たちの簡単な小さなプログラムは動作します。

 func prepare() *Index { i := NewIndex(13 /* ~ 1km */) i.AddUser(1, 14.1313, 14.1313) i.AddUser(2, 14.1314, 14.1314) i.AddUser(3, 14.1311, 14.1311) i.AddUser(10, 14.2313, 14.2313) i.AddUser(11, 14.0313, 14.0313) return i } func TestSearch(t *testing.T) { indx := prepare() found, _ := indx.Search(14.1313, 14.1313, 2000) if len(found) != 3 { t.Fatal("error while searching with radius 2000") } found, _ = indx.Search(14.1313, 14.1313, 20000) if len(found) != 5 { t.Fatal("error while searching with radius 20000") } } $ go test -run 'TestSearch$' PASS ok github.com/mkevac/gophercon-russia-2018/geosearch 0.008s 

しかし、かなり明らかな欠陥が1つあります。 検索範囲が大きく、人口密度が低い場合、get-sで多数のセルを確認する必要があります。 それほど速くはありません。

S2に「キャップ」をstorageLevelレベルのセルでカバーするように依頼したことを思い出してください。 しかし、これらのセルは非常に小さいため、多くのセルが判明します。

S2に、異なるレベルのセルで「キャップ」をカバーするように依頼できます。 次のようになります：

 rc := s2.RegionCoverer{MaxLevel: i.storageLevel} cu := rc.Covering(cap) 

ご覧のとおり、S2は円の内側の大きなセルを使用し、エッジの周りの小さなセルを使用します。 合計すると、セルは小さくなります。

しかし、Bツリー内のより大きなセルからユーザーを見つけるために、Getは使用できなくなりました。 各大きなセルのS2にstorageLevelレベルの最初の内部セルの番号と最後の番号を問い合わせ、範囲スキャン、つまりクエリ「from」と「to」の助けを借りて既に検索する必要があります。

 func (i *Index) SearchFaster(lon, lat float64, radius uint32) ([]uint32, error) { // ... for _, cellID := range cu { if cellID.Level() < i.storageLevel begin := cellID.ChildBeginAtLevel(i.storageLevel) end := cellID.ChildEndAtLevel(i.storageLevel) i.bt.AscendRange(userList{cellID: begin}, userList{cellID: end.Next()},func(item btree.Item) bool { result = append(result, item.(userList).list...) return true }) } else { // ... } } return result, nil } 

変更は非常に小さなものですが、その過程で見てみましょう。 サイクルで検索を行う単純なベンチマークを作成し、実行します。

 var res []uint32 func BenchmarkSearch(b *testing.B) { indx := prepare() for i := 0; i < bN; i++ { res, _ = indx.Search(14.1313, 14.1313, 50000) } } func BenchmarkSearchFaster(b *testing.B) { indx := prepare() for i := 0; i < bN; i++ { res, _ = indx.SearchFaster(14.1313, 14.1313, 50000) } } 

私たちの小さな変化は、3桁の加速をもたらしました。 悪くない！

 $ go test -bench=. goos: darwin goarch: amd64 pkg: github.com/mkevac/gophercon-russia-2018/geosearch BenchmarkSearch-8 500 3097564 ns/op BenchmarkSearchFaster-8 200000 7198 ns/op PASS ok github.com/mkevac/gophercon-russia-2018/geosearch 3.393s 

ジオフェンシングサービスを作成しましょう

半径による検索の超シンプルな実装を検討しました。 同じシンプルなジオフェンシングの実装を簡単に見てみましょう。つまり、どのポリゴンにいるか、またはどのポリゴンに最も近いかを判断します。

ここでもインデックスにはBツリーが必要ですが、それに加えて、追加されたすべてのポリゴンのグローバルマップがあります。

 type Index struct { storageLevel int bt *btree.BTree polygons map[uint32]*s2.Polygon } func NewIndex(storageLevel int) *Index { return &Index{ storageLevel: storageLevel, bt: btree.New(35), polygons: make(map[uint32]*s2.Polygon), } } 

前と同様に、Bツリーのノードにリストを保存しますが、ここではstorageLevelレベルのセルにあるポリゴンのみを保存します。

 type IndexItem struct { cellID s2.CellID polygonsInCell []uint32 } func (ii IndexItem) Less(than btree.Item) bool { return uint64(ii.cellID) < uint64(than.(IndexItem).cellID) } 

この例では、インデックスにポリゴンを追加し、現在のポリゴンを見つけ、最も近いポリゴンを見つける機能があります。

 func (i *Index) AddPolygon(polygonID uint32, vertices []s2.LatLng) error {} func (i *Index) Search(lon, lat float64) ([]uint32, error) {} func (i *Index) SearchNearest(lon, lat float64) ([]uint32, error) {} 

ポリゴンを追加することから始めましょう。 ポリゴンは頂点のリストによって定義され、S2は頂点の順序が反時計回りになることを期待しています。 しかし、エラーの場合、「正規化」の機能があります。それは、それを裏返しにしています。

 func (i *Index) AddPolygon(polygonID uint32, vertices []s2.LatLng) error { points := func() (res []s2.Point) { for _, vertex := range vertices { point := s2.PointFromLatLng(vertex) res = append(res, point) } return }() loop := s2.LoopFromPoints(points) loop.Normalize() polygon := s2.PolygonFromLoops([]*s2.Loop{loop}) // ... return nil } 

頂点のリストをループに変換してから、ポリゴンに変換します。 それらの違いは、多角形が複数のループで構成され、たとえばドーナツのように穴があることです。

前の例のように、S2にポリゴンをセルでカバーし、返された各セルをBツリーに追加するように依頼します。 さて、グローバルマップで。

 func (i *Index) AddPolygon(polygonID uint32, vertices []s2.LatLng) error { // ... coverer := s2.RegionCoverer{MinLevel: i.storageLevel, MaxLevel: i.storageLevel} cells := coverer.Covering(polygon) for _, cell := range cells { // ... ii.polygonsInCell = append(ii.polygonsInCell, polygonID) i.bt.ReplaceOrInsert(ii) } i.polygons[polygonID] = polygon return nil } 

この例では、ポリゴン検索機能は簡単です。 前と同じように、storageLevelレベルでCellIDの検索座標を変換し、Bツリーでこのセルを検索するかどうかを決定します。

 func (i *Index) Search(lon, lat float64) ([]uint32, error) { latlng := s2.LatLngFromDegrees(lat, lon) cellID := s2.CellIDFromLatLng(latlng) cellIDOnStorageLevel := cellID.Parent(i.storageLevel) item := i.bt.Get(IndexItem{cellID: cellIDOnStorageLevel}) if item != nil { return item.(IndexItem).polygonsInCell, nil } return []uint32{}, nil } 

最も近いポリゴンを見つけるのはもう少し複雑です。 まず、突然何らかのトレーニングの場にいるのかどうかを判断しようとします。 そうでない場合は、半径を増やして検索します（以下で、どのように見えるかを示します）。 さて、最も近いポリゴンが見つかったら、それらをフィルタリングして最も近いポリゴンを見つけ、見つかった各ポリゴンまでの距離を計算して、最短距離のポリゴンを取得します。

 func (i *Index) SearchNearest(lon, lat float64) ([]uint32, error) { // ... alreadyVisited := []s2.CellID{cellID} var found []IndexItem searched := []s2.CellID{cellID} for { found, searched = i.searchNextLevel(searched, &alreadyVisited) if len(searched) == 0 { break } if len(found) > 0 { return i.filter(lon, lat, found), nil } } return []uint32{}, nil } 

「半径の増加」とはどういう意味ですか？ 最初の写真では、検索の中心であるオレンジ色のセルが表示されます。 最初に、隣接するすべてのセルで最も近いポリゴンを見つけようとします（図では灰色です）。 そこで何も見つからない場合は、2番目の図のように別のレベルに移動します。 などなど。




「Neighbors」は、AllNeighbors関数によって提供されます。 取得したセルをフィルタリングして、すでに表示したセルを削除する必要がない限り。

 func (i *Index) searchNextLevel(radiusEdges []s2.CellID, alreadyVisited *[]s2.CellID) (found []IndexItem, searched []s2.CellID) { for _, radiusEdge := range radiusEdges { neighbors := radiusEdge.AllNeighbors(i.storageLevel) for _, neighbor := range neighbors { if in(*alreadyVisited, neighbor) { continue } *alreadyVisited = append(*alreadyVisited, neighbor) searched = append(searched, neighbor) item := i.bt.Get(IndexItem{cellID: neighbor}) if item != nil { found = append(found, item.(IndexItem)) } } } return } 

実際、それがすべてです。 この例では、テストも作成しましたが、成功します。

それまたは完全な例を見ることに興味があるなら、スライドと一緒にここでそれらを見つけることができます。

おわりに

座標またはいくつかのより複雑な地理的機能で動作する検索サービスを記述する必要があり、PostGISのような既製のDBMSを使用したくない、または使用できない場合は、S2を検討してください。

これは、基本的なものと座標と地球を操作するためのフレームワークを提供するクールでシンプルなツールです。 Badooの私たちはS2を本当に気に入っており、非常に推奨しています。

よろしくお願いします！

Upd：そして今、ビデオが到着しました！