この記事では、3次元シーンのレンダリングアルゴリズムをExcelの数式（マクロなし）に移植する方法を説明します。

コンピュータグラフィックスに慣れていない人のために、私はすべてのステップをできるだけ簡単かつ簡単に説明しようとしました。 原則として、数式を理解するには、数学の学校コースの知識（+ 3次元マトリックスにベクトルを掛ける能力）で十分です。

また、任意の形状の数式の作成を練習してExcelファイルを生成できる小さなWebアプリケーションを作成しました。

注意：カットの下の19枚の写真と3枚のアニメーション。

どうした

• キューブとトーラスのファイル
• ケトルファイル
• 独自のExcelファイルジェネレーターを備えたObservableHQラップトップ

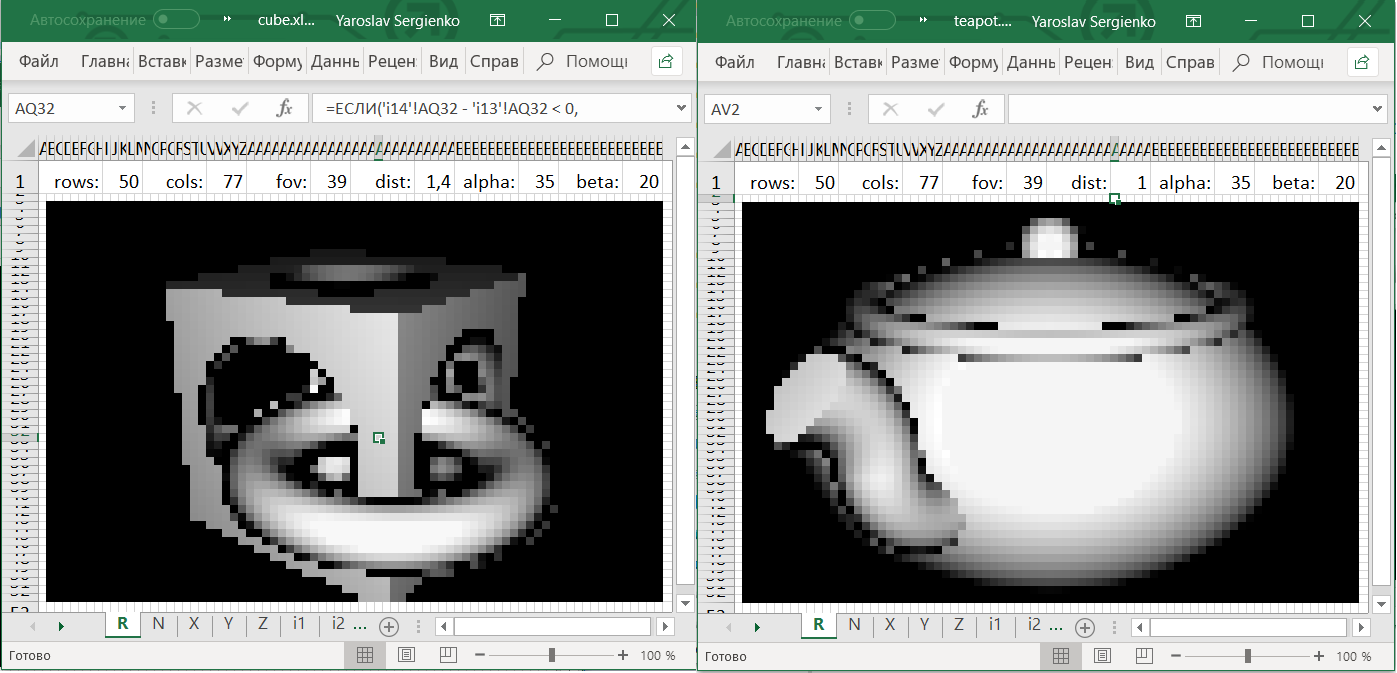
上部のExcelファイルでは、次のセルを変更できます。

• alpha:度単位のカメラの水平回転、
• beta:度単位のカメラの垂直回転、
• dist:カメラから原点までの距離、
• fov:カメラを「ズーム」します。

カメラを回転させるには、Excelにファイルを変更する許可を与える必要があります。

ObservableHQからExcelファイルをダウンロードする場合、セルは手動でペイントする必要があります。 すべての小さな正方形のセルを選択し、「条件付き書式設定」→「カラースケール」を選択する必要があります。

レイマーチング

レイマーチングアルゴリズムは、デモシーン用のコンパクトな3次元エンジンに関する「2つの三角形のある世界のレンダリング」のプレゼンテーションの後、2008年にイニゴキレスによって普及しました。

その後、 IñigoQuilezがShadertoyの Webサイトを作成し、 そこに投稿された作業のほとんどが説明された手法を使用しています。 これにより、例えばこのギャラリーのようなフォトリアリスティックなシーンを作成できることがわかりました。

レイマーチングは非常に実装しやすく効率的なアルゴリズムで、非常に複雑なシーンをレンダリングできます。 なぜそれはビデオカードで使用されないのですか？ 事実、ビデオカードは、レイマーチングがそれほど効果的ではない三角形で構成される3次元の図形を扱うために研ぎ澄まされています。

更新：この方法の欠点については、 DrZlodbergからのこのコメントも参照してください。

エンジンの原理

• オブジェクトは関数として記述されます。
• 結果の各ピクセルをカメラから出る光線と一致させます。
• 各光線について、オブジェクトとの交差点の座標を見つけます。
• 交点を使用して、ピクセルの色を決定します。

何らかの形で、これらすべてのサブタスクは3次元エンジンで解決されると思います。

プロパティの説明

3次元オブジェクトを記述する方法は3つあります。

• カメラから出る光線によってオブジェクトとの交点（または、たとえば、その中の接線の方向）を返す明示的な数式。
• メンバーシップ機能。 空間内のポイントごとに、オブジェクトに属しているかどうかを報告します。
• 実機能。 オブジェクトの内側のポイントの場合は負で、外側のポイントは正です。

この記事では、3番目のオプションの特別なケース、 符号付き距離関数（SDF）を使用します。

SDFは空間内のポイントを受け取り、オブジェクト内の最も近いポイントまでの距離を返します。 内部のポイントの場合は、マイナス記号が付いたオブジェクトの境界までの距離に等しい

ビームとオブジェクトの交差点を見つける

カメラからの光線があり、オブジェクトとの交点を見つけたいとします。

この点を見つけるには、いくつかの方法があります。

• 特定のステップでビーム上のポイントを通過します。
• オブジェクトの内側と外側にポイントがあり、バイナリ検索を実行して交差を指定します。
• または、光線で制限されたSDF関数（オブジェクト内部では負、外部では正）の根を見つけるための方法を開始します。

しかし、ここでは別の方法を使用します： Ray Marching 。

これは、SDFでのみ機能する単純なアルゴリズムです。



関数によって開始からの距離で光線をパラメーター化しましょう $$$ray（t）=（x、y、z）$ 。
それから $$$光線（0）$ -これはカメラ自体です。 アルゴリズムは次のとおりです。

• $$$t = 0$
• 繰り返す $$$N$ 回：
  
  • $$$t = t + SDF（ray（t））$
• もし $$$t <TMax$ その後戻ります $$$光線（t）$ そうでなければ、ビームがオブジェクトと交差しないことを通知します。

ここに $$$N$ 余裕がある反復回数。
以上 $$$N$ 、アルゴリズムがより正確になります。

数 $$$TMax$ これは、オブジェクトを見つけることができるカメラからの距離です。

アルゴリズムが機能する理由

アルゴリズムは常にオブジェクトとの交点に到達しますか？ オブジェクトは複雑な形状を持つことができ、他の部分はビームに近づけることができ、アルゴリズムが交差点に収束するのを防ぎます。 実際、これはできません。オブジェクトの他の部分は、レイからゼロ以外の距離にある必要があります（そうでなければ、交差します）。 $$$\ delta> 0$ 。 次に、SDF関数が大きくなります $$$\デルタ$ 光線の任意の点（交差点に非常に近い点を除く）。 したがって、遅かれ早かれ彼は交差点に近づきます。


一方、アルゴリズムが特定のポイントに収束する場合、隣接する反復間の距離はゼロになる傾向があります $$$\右矢印$ SDF（オブジェクトの最も近い点までの距離）もゼロになる傾向があります $$$\右矢印$ 限界に $$$SDF = 0$$$$\右矢印$ アルゴリズムは、ビームとオブジェクトの交差点に収束します。

交点のピクセルの色を取得する

各ピクセルについて、オブジェクトとの交点を見つけたと想像してください。 これらの値（つまり、カメラから交差点までの距離）を直接描画して、これらの写真を取得できます。



これはExcelを使用して取得されたものであり、悪くないことを考えると。 しかし、色を人生のオブジェクトを見るようなものにすることは不可能かどうかを知りたいです。

コンピュータグラフィックスでは、色を計算する基本的な方法はフォンシェーディングです。 Phongによれば、結果の色は、背景、ミラー、拡散の3つのコンポーネントで構成されます。 フォトリアリスティックレンダリングに努めていないという事実を考えると、拡散コンポーネントのみを使用すれば十分です。 このコンポーネントの式は、 ランバートの法則に従い、ピクセルの色は、表面の法線と光源の方向の間の角度の余弦に比例することを示しています。

さらに、計算を簡素化するために、光源とカメラが同じであると仮定します。 次に、実際には、カメラからのビームとオブジェクトの表面の間の角度のサインを見つける必要があります。


望ましい角度 $$$\ varphi$ 図面で1つの円弧をマークしました。 そのサインの値は次のように示されます $$$k$ 。

通常、レイマーチング法を使用する場合、オブジェクトの法線を見つけるには、次の手順を実行します：交差点の隣の6点でSDF値を計算し（点の数を4に減らすのは簡単です）、この関数の勾配を見つけます。 これはExcelにとって計算が多すぎるように思えたので、希望の角度を簡単に見つけたいと思います。

アルゴリズムの収束率を見ると、ビームとオブジェクト間の角度がまっすぐであれば、1回の反復で十分であることがわかります。 角度が小さい場合、アルゴリズムは非常にゆっくり収束します。

アルゴリズムの収束率に基づいて、表面に対する角度に関する情報を取得することは可能ですか？ この場合、追加の計算はまったく必要ありません。前の反復の値を分析するだけで十分です。

図面を描きます。 示す $$$I_n$ そして $$$I_ {n + 1}$ -アルゴリズムの隣接する反復で得られたポイント。 ポイントがオブジェクトに十分に近く、プレーン、つまり検索する角度に置き換えることができると仮定します。 させる $$$R = SDF（I_n）$ 、 $$$r = SDF（I_ {n + 1}）$ -ポイントからの距離 $$$I_n$ そして $$$I_ {n + 1}$ 飛行機に。 次に、アルゴリズムに従って、間の距離 $$$I_n$ そして $$$I_ {n + 1}$ 等しい $$$R$ 。



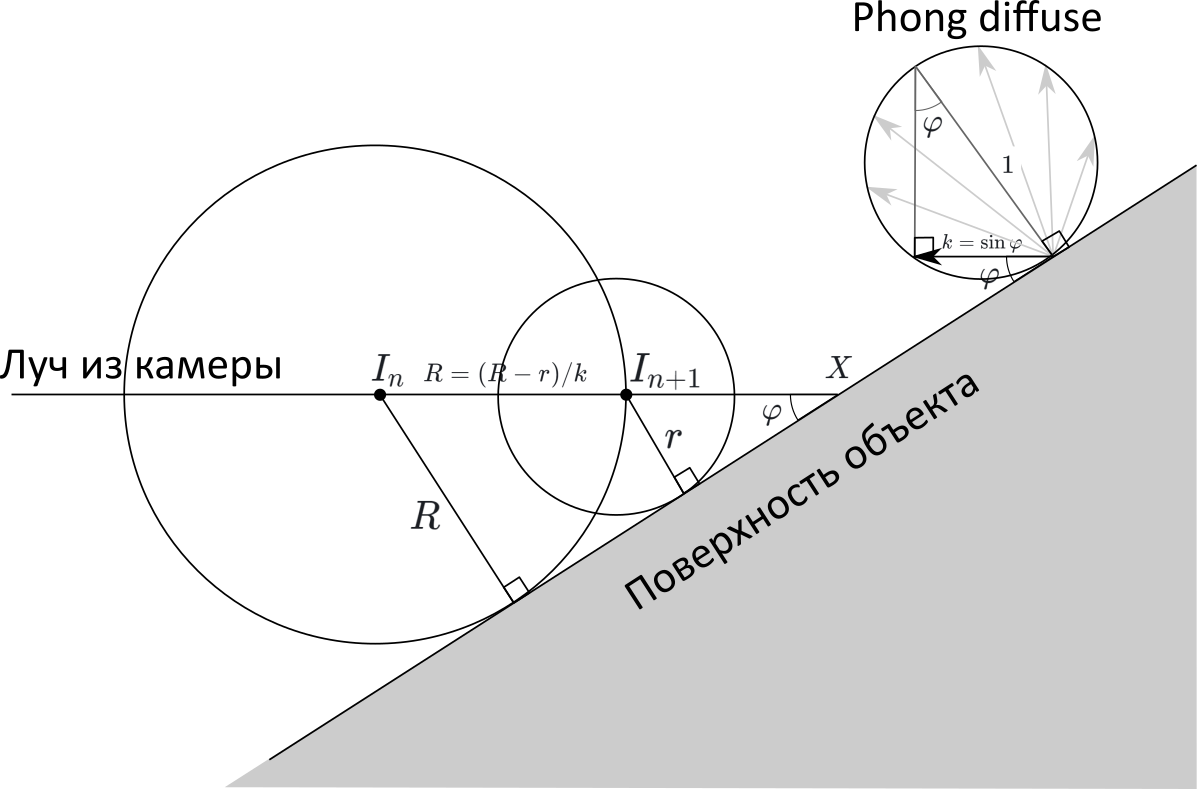
一方、 $$$X$ 光線と図形の交点です
$$$I_nX = R / k$ 、そして $$$I_ {n + 1} X = r / k$ したがって

$$

$$R = I_nI_ {n + 1} = I_nX-I_ {n + 1} X = \ frac {R-r} {k}$$

$$

$$k = \ frac {R-r} {R} = 1-\ frac {r} {R} = 1-\ frac {SDF（I_ {n + 1}）} {SDF（I_ {n}）}$$

つまり、ピクセル強度は、1から隣接する反復のSDF関数の比率を引いたものに等しくなります！

シンプルな形状を説明します

球体、立方体、トーラスのSDFの例：

$$$\ sqrt {x ^ 2 + y ^ 2 + z ^ 2}-r$
$$$\ max（| x |、| y |、| z |）-side / 2$
$$$\ sqrt {（\ sqrt {x ^ 2 + z ^ 2}-R）^ 2 + y ^ 2}-r$

シェイプは、軸に沿って移動および圧縮できます。

$$$キューブ（x、y + 0.3、z）$
$$$キューブ（x、2 \ cdot y、z）$

シェイプを結合、交差、減算することもできます。 つまり、SDFは構造ソリッドジオメトリの基本操作をサポートします。

$$$\ min（球体（x、y、z）、立方体（x、y、z））$
$$$\ max（球体（x、y、z）、立方体（x、y、z））$
$$$\ max（-sphere（x、y、z）、cube（x、y、z））$

注意深い読者は、いくつかの図形（たとえば、立方体）と一部の操作（たとえば、圧縮）で、上記の式が常にオブジェクトの最も近い点までの距離を返すわけではないことに気づく場合があります。つまり、正式にはSDFではありません。 それにもかかわらず、それらはまだSDFエンジン入力に供給でき、正しく表示されることが判明しました。

これはSDFでできることのほんの一部です。形状と操作の完全なリストはwww.iquilezles.org/www/articles/distfunctions/distfunctions.htmにあります。

上記のすべての式を組み合わせて、最初の図を取得します。

$$$\ min（\\ \ quad \ max（| x |-0.3、| y |-0.3、| z |-0.3、-\ sqrt {x ^ 2 + y ^ 2 + z ^ 2} + 0.375）、\ \ \ quad \ sqrt {（\ sqrt {（x-0.25）^ 2 +（z-0.25）^ 2}-0.25）^ 2 + y ^ 2}-0.05 \\）$

ケトル式

やかんはもう少し複雑です：計画が必要です



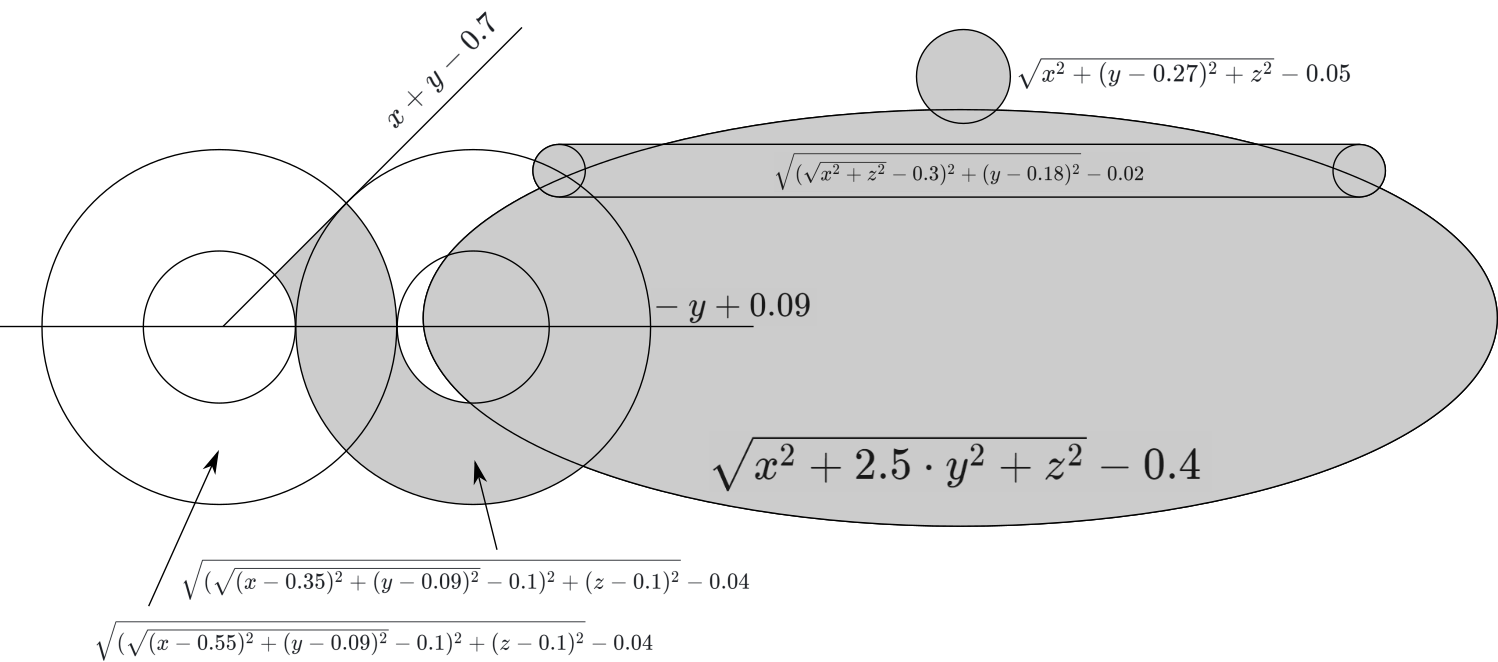
式を注意深く書き留めます。

$$$\ min（\\ \ quad \ sqrt {x ^ 2 +（y-0.27）^ 2 + z ^ 2}-0.05 \\ \ quad \ sqrt {x ^ 2 + 2.5 \ cdot y ^ 2 + z ^ 2 }-0.4、\\ \ quad \ sqrt {（\ sqrt {x ^ 2 + z ^ 2}-0.3）^ 2 +（y-0.18）^ 2}-0.02、\\ \ quad \ max（\\ \ qquad x + y-0.7、\\ \ qquad-y + 0.09、\\ \ qquad \ sqrt {（\ sqrt {（x-0.55）^ 2 +（y-0.09）^ 2）-0.1} ^ 2 +（ z-0.1）^ 2}-0.04、\\ \ quad）、\\ \ quad \ max（\\ \ qquad-（-y + 0.09）、\\ \ qquad \ sqrt {（\ sqrt {（x-0.35 ）^ 2 +（y-0.09）^ 2}-0.1）^ 2 +（z-0.1）^ 2}-0.04、\\ \ quad）、\\）$

そして、希望の角度を選択します。 完了：

---

カメラ

残っているのは、画面上の特定のピクセルについて、カメラから出てくる空間内の対応する光線を見つけることだけです。 より正確には、カメラまでの距離でこのビームのポイントを見つけることができる必要があります。 つまり、関数が必要です $$$ray（s、t、d）$ どこで $$$s、t$ ピクセルの座標であり、 $$$d$ -ビームの開始点からの距離（カメラ）。

計算の便宜上、ピクセルの座標は画面の中心を基準にして設定されます。 画面が $$$行$ 行と $$$cols$ 列、我々は内の座標を期待する $$$s \ in \ left [-\ frac {cols} {2}、\ frac {cols} {2} \ right]、t \ in \ left [-\ frac {rows} {2}、\ frac {rows} {2} \右]$



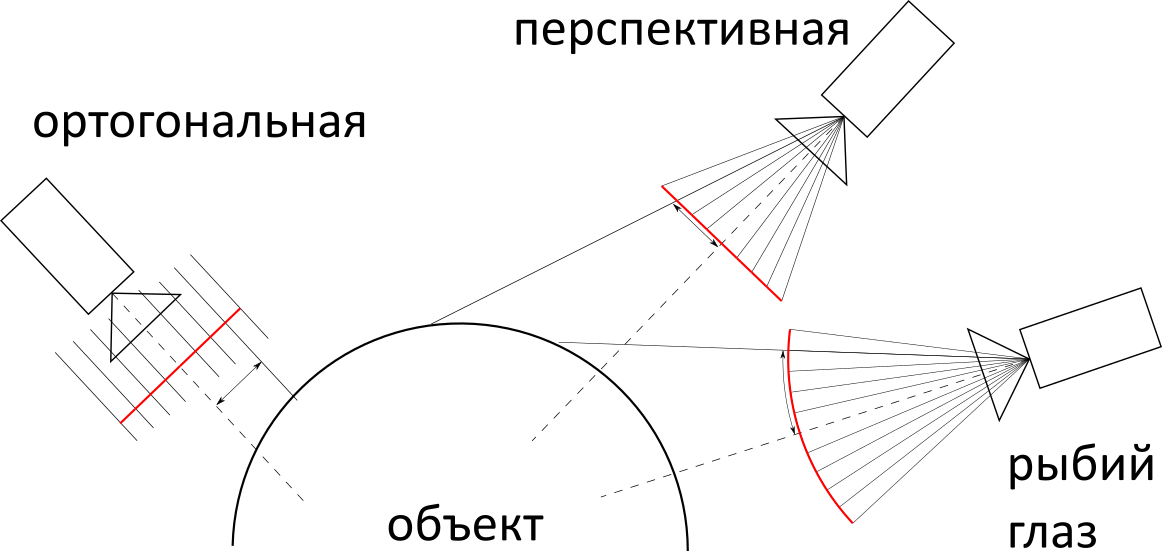
次に、カメラの投影のタイプを決定する必要があります：直交、遠近法、または「魚眼」。 実装の複雑さに関しては、それらはほぼ同じですが、実際には最も有望なものが最も頻繁に使用されるため、それを使用します。



この章のほとんどの計算は、たとえばカメラをある地点に置くことで回避できたはずです。 $$$（1、0、0）$ 軸に沿った方向付け $$$X$ 。 しかし、数字も軸に沿って整列しているという事実を考慮すると、結果はあまり面白くない角度になります。 そのため、立方体の場合、正方形と見なされます。

カメラを回転させる機能を提供するには、 オイラー角を使用して多くの計算を慎重に実行する必要があります。 したがって、入力で3つの変数を取得します。角度 $$$\ alpha$ 角度 $$$\ベータ$ と距離 $$$dist$ 。 それらはカメラの位置と方向の両方を決定します（カメラは常に原点を見ます）。

WolframAlphaを使用して、回転行列を見つけます。

$$

$$\ begin {pmatrix} x \\ y \\ z \ end {pmatrix} = \ underbrace {\ begin {pmatrix} \ cos（\ alpha）\ cos（\ beta）＆-\ cos（\ alpha）\ sin（ \ beta）＆\ sin（a）\\ \ sin（\ beta）＆\ cos（\ beta）＆0 \\-\ cos（\ beta）\ sin（\ alpha）＆\ sin（\ alpha）\ sin （\ beta）＆\ cos（\ alpha）\ end {pmatrix}} _ {M（\ alpha、\ beta）} \ begin {pmatrix} x '\\ y' \\ z '\ end {pmatrix}$$

ベクトルに適用する場合 $$$（dist、0、0）$ 、カメラの座標を取得します（マイナスが消えた場所を聞かないでください）：

$$

$$\ begin {pmatrix} camX \\ camY \\ camZ \ end {pmatrix} = M（\ alpha、\ beta）\ begin {pmatrix} dist \\ 0 \\ 0 \ end {pmatrix} = dist \ begin {pmatrix } \ cos（\ alpha）\ cdot \ cos（\ beta）\\ \ sin（\ beta）\\ \ sin（\ alpha）\ cdot \ cos（\ beta）\ end {pmatrix}$$

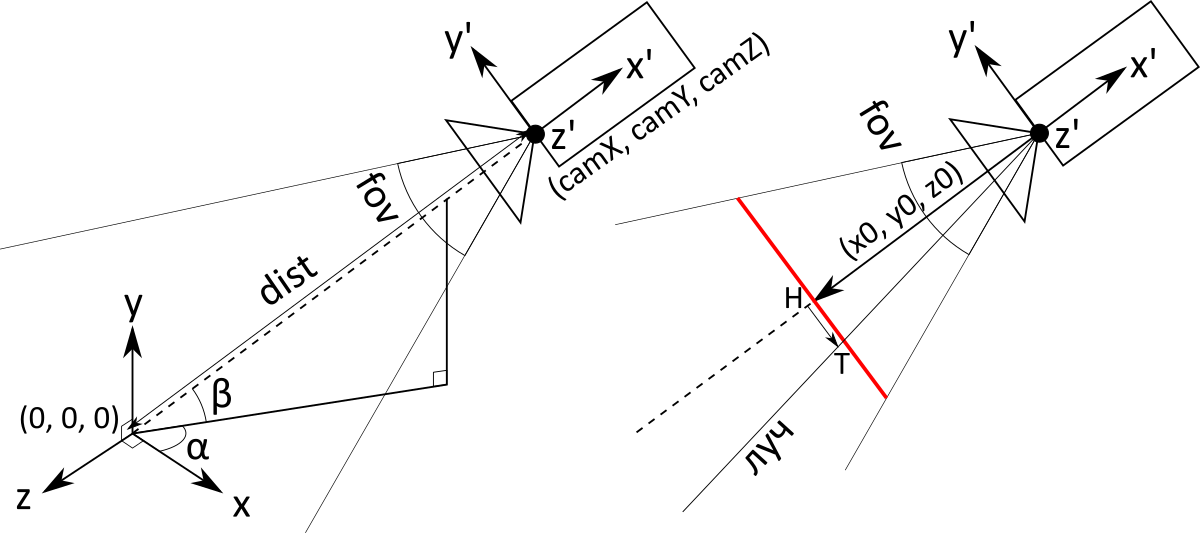
後続の計算は、透視投影に固有のものになります。 主なオブジェクトは画面です （図では赤、イタリック体ではテキスト）。 これは、カメラの前にある距離にある想像上の長方形であり、ご想像のとおり、通常の画面のピクセルと1対1で対応しています。 カメラは実際には座標を持つ単なるポイントです $$$（camX、camY、camZ）$ 。 ピクセルに対応する光線は、カメラのポイントから始まり、 画面上の対応するポイントを通過します 。

画面には正確な場所とサイズがありません。 より正確には、それらはカメラまでの距離に依存します。画面をさらに移動する場合は、さらに行う必要があります。 したがって、カメラからスクリーンまでの距離は1であることに同意します。その後、ベクトルの値を計算できます $$$（x0、y0、z0）$ カメラのポイントと画面の中心を接続します（カメラの中心と同じです。 $$$dist$ でも $$$-1$ ）：

$$

$$\ begin {pmatrix} x0 \\ y0 \\ z0 \ end {pmatrix} = M（\ alpha、\ beta）\ begin {pmatrix} -1 \\ 0 \\ 0 \ end {pmatrix} =-\ begin { pmatrix} \ cos（\ alpha）\ cdot \ cos（\ beta）\\ \ sin（\ beta）\\ \ sin（\ alpha）\ cdot \ cos（\ beta）\ end {pmatrix}$$

次に、 画面サイズを決定する必要があります 。 これはカメラの視野角に依存します。視野角は度単位で測定され、ビデオカメラの「ズーム」と呼ばれるものに対応します。 ユーザーは変数を使用して設定します $$$fov$ （視野）。 画面は正方形ではないため、垂直視野角の意味を明確にする必要があります。

そのため、画面の高さを決定するには、頂点角を持つ二等辺三角形の底辺を見つける必要があります $$$fov$ 高さ1：三角法を覚えて、私たちは得る $$$2 \ tan \左（fov / 2 \右）$ 。 これに基づいて、 画面上の1ピクセルのサイズを決定できます 。

$$

$$pixelSize = \ frac {2 \ tan \ left（fov / 2 \ right）} {rows}$$

次に、回転行列をベクトルに適用します $$$（0、0、1）$ そして $$$（0、1、0）$ ベクトルを取得します $$$\上線{u}$ そして $$$\上線{v}$ 画面の水平方向と垂直方向を定義します （計算を簡素化するために、これらは事前に乗算されます $$$pixelSize$ ）：

$$

$$\ begin {pmatrix} ux \\ uy \\ uz \ end {pmatrix} = pixelSize \ cdot M（\ alpha、\ beta）\ begin {pmatrix} 0 \\ 0 \\ 1 \ end {pmatrix} = pixelSize \ begin {pmatrix} \ sin（\ alpha）\\ 0 \\ \ cos（\ alpha）\ end {pmatrix}$$

$$

$$\ begin {pmatrix} vx \\ vy \\ vz \ end {pmatrix} = pixelSize \ cdot M（\ alpha、\ beta）\ begin {pmatrix} 0 \\ 1 \\ 0 \ end {pmatrix} = pixelSize \ begin {pmatrix} \ cos（\ alpha）\ cdot \ sin（\ beta）\\ \ cos（\ beta）\\ \ sin（\ alpha）\ cdot \ cos（\ beta）\ end {pmatrix}$$

したがって、カメラを出て、座標を持つピクセルに対応するビームの方向を見つけるためのすべてのコンポーネントがあります $$$s、t$

$$

$$raydir（s、t）= \ begin {pmatrix} x0 \\ y0 \\ z0 \ end {pmatrix} + s \ begin {pmatrix} ux \\ uy \\ uz \ end {pmatrix} + t \ begin {pmatrix } vx \\ vy \\ vz \ end {pmatrix}$$

これはほとんど必要なものです。 光線の開始点がカメラのポイントにあり、方向ベクトルを正規化する必要があることのみを考慮する必要があります。

$$

$$ray（s、t、d）= \ begin {pmatrix} camX \\ camY \\ camZ \ end {pmatrix} + d \ cdot \ frac {raydir（s、t）} {\ lVert raydir（s、t） \ rVert}$$

目的の機能が得られました $$$ray（s、t、d）$ ある距離でビームのポイントを返す $$$d$ 座標を持つピクセルに対応する最初から $$$s、t$ 。

エクセル

結果のExcelファイルは、6枚以上で構成される本です。

• Rの最初のシートには、エンドユーザーが必要とするすべてのものが含まれます。パラメーターを持つセル $$$rows、cols、fov、alpha、beta、dist$ 、および結果のセルを白黒のスケールでペイントします。
• シートNは値を予測します $$$\ frac {1} {\ lVert raydir（s、t）\ rVert}$ 。
• シートX 、 Y 、 Zは座標を計算します $$$X、Y、Z$ ベクトル $$$raydir（s、t）$ そして $$$\ frac {raydir（s、t）} {\ lVert raydir（s、t）\ rVert}$ 。
• シートi1 、 i2 、...には、各ピクセルのレイマーチングアルゴリズムの反復が含まれています。

すべてのシートは同じ方法で作成されます。

• 最初の行には、1〜6個の「グローバル」変数（青）が含まれています。 それらはすべてのシートで使用できます。
• シートの大部分はピクセル計算（緑）で占められています。 これはサイズの長方形です $$$rows \ times cols$ 。 記事の最後にある表では、これらのセルは**として示されています。
• シートX 、 Y、およびZも行と列（オレンジ）の中間計算を使用します。 2行目と1列目は予約されています。 記事の最後にある表では、これらのセルはA*および*2示されています。 アイデアは値を保存することです $$$raydir（s、t）$ すべてのピクセルについて、その計算式は2つのコンポーネントの合計に分割されるため、（各座標に対して）さらに3つのシートを追加する必要はありません。
  

  $$

  $$raydir（s、t）= \ underbrace {\ begin {pmatrix} x0 \\ y0 \\ z0 \ end {pmatrix} + s \ begin {pmatrix} ux \\ uy \\ uz \ end {pmatrix}} _ { \ mbox {column}} + \ underbrace {t \ begin {pmatrix} vx \\ vy \\ vz \ end {pmatrix}} _ {\ mbox {row}}$$
  
  したがって、列の最初の項と行の2番目の項を計算し、値を取得する必要がある場合 $$$raydir（s、t）$ 、行のセル値を追加します $$$s$ と列 $$$t$ 。
  

シートR
I1	行：	50
V1	cols：	77
AI1	fov：	39
AV1	dist：	1,4
BI1	アルファ：	35
Bv1	ベータ：	20
**	=(i14! XN - i13! XN < 0,00000000000001; 0,09; (0; (1; (i15! XN - i14! XN ) / (i14! XN - i13! XN ))))

シートN
I1	pixelSize：	=TAN(R!AI1 / 2) / (R!I1 / 2)
**	=1 / ((X!A N + X! X 2; 2) + (Y!A N ; 2) + (Z!A N + Z! X 2; 2))

シートX
I1	camX：	=R!AV1 * COS(R!BV1) * COS(R!BI1)
V1	ux：	=-N!I1 * SIN(R!BI1)
AI1	vx：	=N!I1 * SIN(R!BV1) * COS(R!BI1)
AV1	x0：	=-COS(R!BV1) * COS(R!BI1)
A *	=AI1 * (() - 2 - (R!I1 + 1) / 2)
* 2	=AV1 + V1 * (() - 1 - (R!V1 + 1) / 2)
**	=( Z 2 + A N ) * N! Z N

シートy
I1	キャミ：	=R!AV1 * SIN(R!BV1)
V1	vy：	=-N!I1 * COS(R!BV1)
AI1	y0：	=-SIN(R!BV1)
A *	=AI1 + V1 * (() - 2 - (R!I1 + 1) / 2)
**	=A N * N! Z N

シートz
I1	camZ：	=R!AV1 * COS(R!BV1)) * SIN(R!BI1)
V1	uz：	= N!I1 * COS(R!BI1)
AI1	vz：	= N!I1 * SIN(R!BV1) * SIN(R!BI1)
AV1	z0：	=-COS(R!BV1) * SIN(R!BI1)
A *	=AI1 * (() - 2 - (R!I1 + 1) / 2)
* 2	=AV1 + V1 * (() - 1 - (R!V1 + 1) / 2)
**	=( Z 2 + A N ) * N! Z N

シートi1
I1	dist0：	= formula( X!I1, Y!I1, Z!I1 )
**	=I1 + formula( X!I1 + X! XN * I1, Y!I1 + Y! XN * I1, Z!I1 + Z! XN * I1 )

シートi2 、 i3 、...
**	=i (n-1) ! XN + formula( X!I1 + X! XN * i (n-1) ! XN , Y!I1 + Y! XN * i (n-1) ! XN , Z!I1 + Z! XN * i (n-1) ! XN )

注：

• Excelはラジアンで計算するため、すべての三角関数の引数に乗算されます $$$\ frac {\ pi} {180}$ （ExcelにはこれのためのRADIANS関数があります）。 数式を混同しないように、上記の表からこれらの乗算を削除しました。
• formulaが記述されている場合、次の式のいずれかを挿入する必要があります。
  
  
  エクセルトーラスキューブフォーミュラ

   MIN（
     MAX（
       ABS（x）-0.3、ABS（y）-0.3、ABS（z）-0.3、
       -SQRT（POWER（x、2）+ POWER（y、2）+ POWER（z、2））+ 0.375
     ）、
     SQRT（POWER（SQRT（POWER（x-0.25、2）+ POWER（z-0.25、2））-0.25、2）+ POWER（y、2））-0.05
   ）
  

  
  
  
  
  Excelのケトル式

   MIN（
     SQRT（POWER（SQRT（POWER（x、2）+ POWER（z、2））-0.3、2）+ POWER（y-0.18、2））-0.02、
     SQRT（POWER（x、2）+ POWER（y、2）* 2.5 + POWER（z、2））-0.4、
     MAX（
       x + y-0.15-0.05-0.5、
       -（y）+ 0.19-0.1、
       SQRT（POWER（SQRT（POWER（x-0.55、2）+ POWER（y-0.09、2））-0.1、2）+ POWER（z-0.1、2））-0.04
     ）、
     MAX（
       -（-（y）+ 0.19-0.1）、
       SQRT（POWER（SQRT（POWER（x-0.35、2）+ POWER（y-0.09、2））-0.1、2）+ POWER（z-0.1、2））-0.04
     ）、
     SQRT（POWER（x、2）+ POWER（y-0.27、2）+ POWER（z、2））-0.05
   ）
  

  
  
  
  

この記事は、記事「MS Excelの数式で書かれた3Dエンジン」とどのように関連していますか

このエンジンは、迷路と楕円体のレンダリングにのみ適しています。 一次元のレイキャスターが使用され、そこから上下のストライプが描かれ、壁の錯覚を作り出します。 しかし、その後、本格的なゲームロジックが実装されます。ここでは、目標は3次元エンジンのみです。