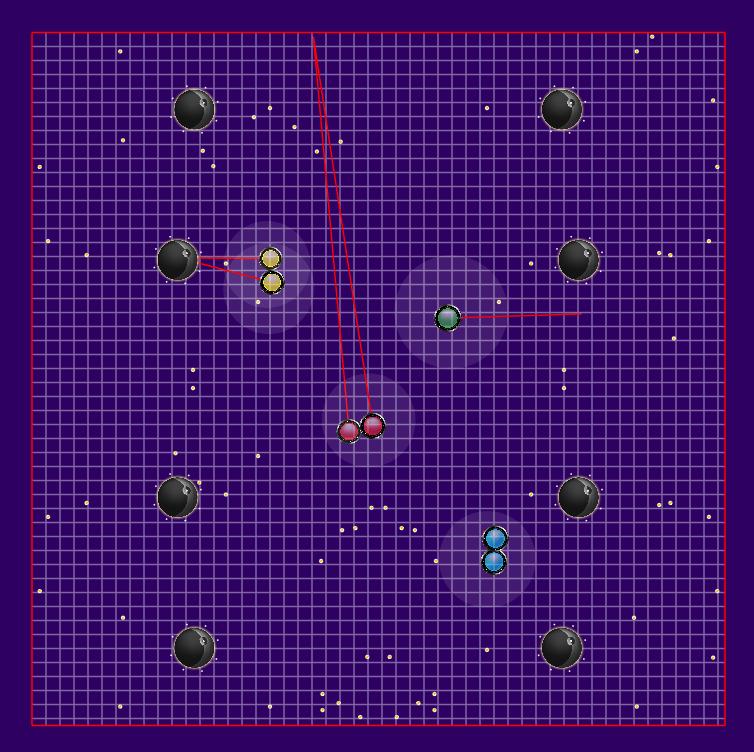
競争では、MiniAICup#2 Almost Agar IOはアメーバを制御し、食べ物や他のアメーバを食べる必要があります。
アメーバ制御アルゴリズムを実装するために、潜在的なフィールドはそれ自体を示唆しますが、1つの大きなBUTがあります。
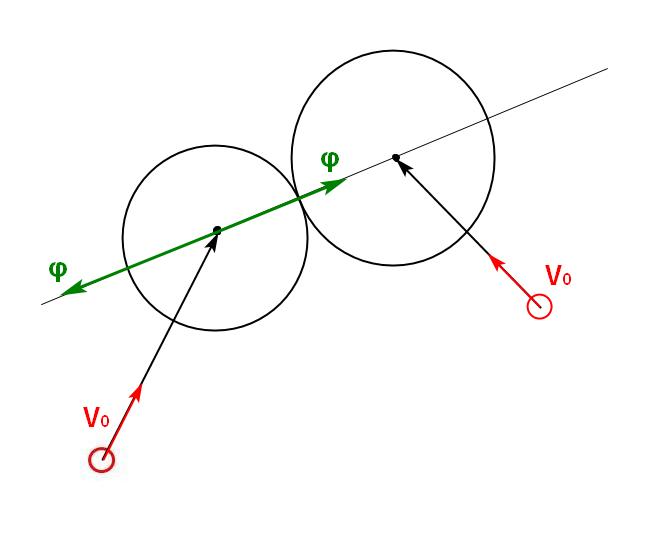
ゲームの動きの物理は、次の方程式によって定義されます。
speed_x + =(nx * max_speed-speed_x)* INERTION_FACTOR /質量;
speed_y + =(ny * max_speed-speed_y)* INERTION_FACTOR /質量;
摩擦と慣性を伴う物理学が判明し、すべてが損なわれます。 物理学を考慮せず、力ベクトル(nx)を最も近いターゲットに直接向けると、次のようになります。

食物と敵を最適に食べるために、これらの方程式を考慮に入れなければなりません。
始めるために、それらを便利なベクタービューに表示します。
$$表示$$ \ vec V_n = \ vec V_ {n-1} +(\ vec \ varphi * V_m-\ vec V_ {n-1})* \ mu \\ \ vec X_n = \ vec X_ {n- 1} + \ vec V_n \\ \ varphi-\ textrm {力ベクトル(そのモジュールが1であることを忘れないでください)} \\ V_m-\ textrm {最高速度} \\ \ mu-\ textrm {INERTION_FACTOR} / mass $$表示$$
だから、食べ物のあるフィールドがあります。 フィールドには、既知の座標と速度を持つ独自のアメーバがあります。 食べ物をできるだけ早く食べるためには、力ベクトルをどの方向に適用するかを計算する必要があります。
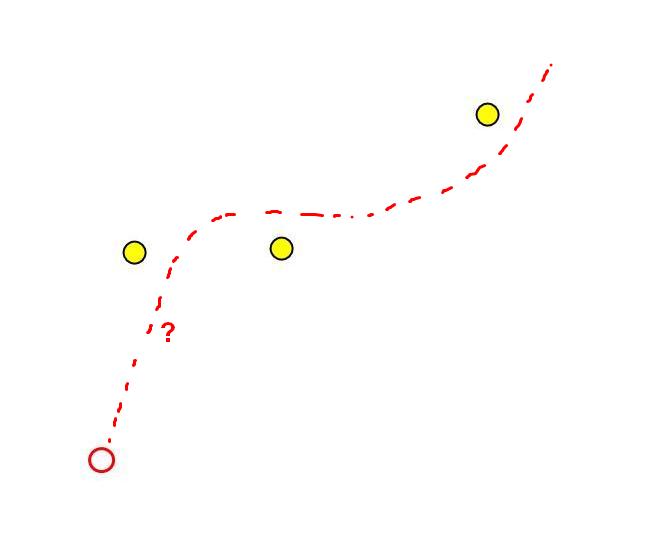
軌道計算
最も明白なオプションは次のとおりです。
次のTステップでは、力ベクトルφを変更せず、K方向の力の適用を選択し、各方向の運動の軌跡を計算すると仮定します。 軌跡の各ポイントで、食べ物を食べることができるかどうかを確認します。
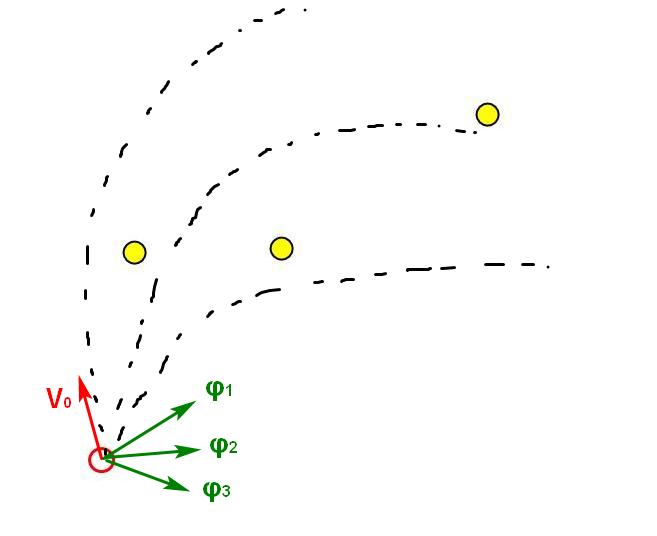
上記の方程式を使用すると、軌道の計算は非常に簡単かつ高速になりますが、このアプローチの複雑さは急速に増大します。 各軌跡の各ポイントで、各アメーバが各食事に到達するかどうかを考慮する必要があります。
私たちが持っています:
これらの数値はすべて乗算されます。 アメーバがいくつかの部分に分割されている場合、それらが大きな表示半径を持っている場合、彼らは多くの食物を見るため、計算アルゴリズムは計算に割り当てられた20ミリ秒に収まりません。
それにもかかわらず、いくつかの最適化を備えたこのような食品検索アルゴリズムは、上位52に簡単に収まります。
運動方程式の解析解
V0とX0の初期値を使用すると、n番目のステップで軌道上の任意の点をすぐに計算できます。
単純な変換による運動方程式は次のようになります。
vecVn= vec varphi∗Vm+( vecV0− vec varphi∗Vm)∗(1− mu)n vecXn= vecX0+ vec varphi∗n∗Vm+( vecV0− vec varphi∗Vm)∗(1− mu)∗ frac1−(1− mu)n mu
心配しないでください。 特に座標の方程式は恐ろしく見えますが、単純に計算されます。 ここで、VnとXnは時間の初期条件X0とV0のみに依存します。
これらの方程式を使用して、事前に決められた食事までの距離が最小になるステップnをすぐに推測することができます。
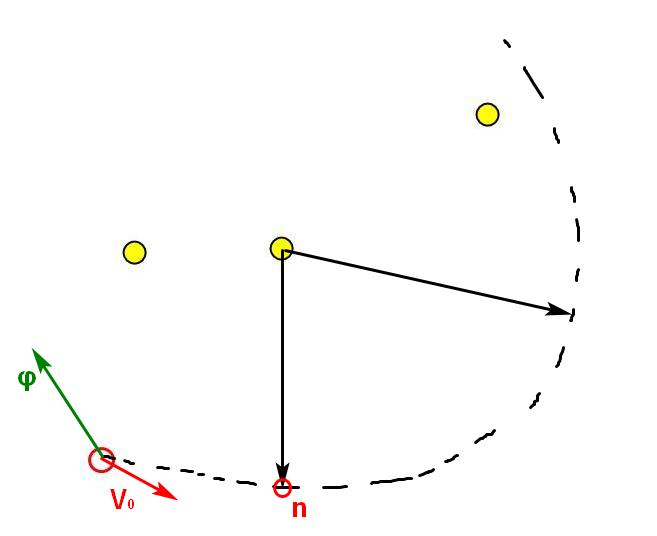
このようなアプローチは、コンピューティングリソースを大幅に節約します。 各食事から軌道上の各ポイントまでの距離を計算する必要はありません。
しかし、分析的にそのような点の数を推測することは私にとってうまくいきませんでした。 したがって、私は黄金比アルゴリズムを使用して、特定の食事までの最短距離を持つポイントを検索しました。
パスの長さが100ティックの場合、このアプローチでは合計10ポイントを計算して、食事に最も近いポイントを見つける必要があります。
ただし、説明した最初の方法では、長さが100ティック未満の軌道の計算時間が短くなることがテストにより示されました。 ラムダが使用されているか、何らかのエラーが原因である可能性があります。
到達可能エリア
n番目のステップで座標方程式を注意深く見ると、次のことがわかります。
vecXn= vecX0+ vecV0∗crap(n)+ vec varphi∗その他のがらくた(n)
力のモジュラスφは1であることに注意してください。
力φの方向に関係なく、時間nの後、アメーバは円(すべてのステップnで力が常に一方向に向けられている場合)、または円の内側(力がnステップ中に変化した場合)に現れます。
円の中心と半径:
vecOn= vecX0+ vecV0∗crap(n)Rn= vec varphi∗その他のがらくた(n)
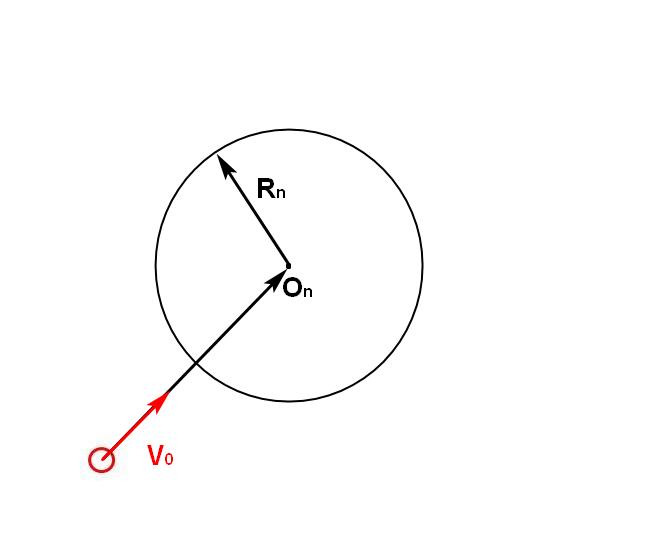
これは手の届く範囲です! nステップで、アメーバは確かにこのエリア内またはその境界にあります!
これはどのように使用しますか?
食品指導
到達可能領域の境界が食物に触れるようなステップnを見つける必要があります。 食物の到達可能領域の中心からベクトルを取ります。 これは、アメーバができるだけ早く食べ物に近づくように求める力の望ましい方向になります。
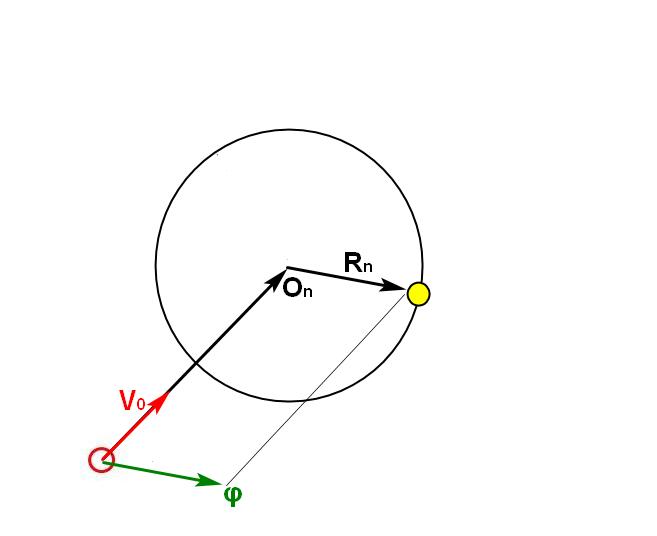
敵の誘導と回避
敵にも独自の到達範囲があります。 自分と敵の手の届くところに触れることができるステップを見つける必要があります。 敵を捕まえる必要がある場合は、2つの到達可能領域の中心を結ぶ線に沿って力ベクトルを向ける必要があります。
逃げる必要がある場合は、力ベクトルを反対方向に向ける必要があります。