はじめに
このシリーズの前回の
記事では 、データ分析の問題に関するステートメントについて説明し、機械学習モデルのセットアップの最初のステップを踏んで、アプリケーションプログラマーが使用するのに便利なインターフェイスを作成しました。 今日は、問題のさらなる調査を実施します。新しい機能を実験し、より複雑なモデルとチューニングパラメーターのオプションを試します。
可能な限り、この記事では、コミュニティで確立された英語の用語と俗語の文字通りの翻訳に基づいて、著者が選択したロシア語の用語を使用しています。 あなたは
ここでそれについて読むことができ
ます 。
モデルを調整し、検証サンプルでの予測の品質を評価するという点で決めたことを思い出しましょう。
現在のコード[research.py] import pickle import math import numpy from sklearn.linear_model import LinearRegression TRAIN_SAMPLES_NUM = 20000 def load_data(): list_of_instances = [] list_of_labels =[] with open('./data/competition_data/train_set.csv') as input_stream: header_line = input_stream.readline() columns = header_line.strip().split(',') for line in input_stream: new_instance = dict(zip(columns[:-1], line.split(',')[:-1])) new_label = float(line.split(',')[-1]) list_of_instances.append(new_instance) list_of_labels.append(new_label) return list_of_instances, list_of_labels def is_bracket_pricing(instance): if instance['bracket_pricing'] == 'Yes': return [1] elif instance['bracket_pricing'] == 'No': return [0] else: raise ValueError def get_quantity(instance): return [int(instance['quantity'])] def get_min_order_quantity(instance): return [int(instance['min_order_quantity'])] def get_annual_usage(instance): return [int(instance['annual_usage'])] def get_absolute_date(instance): return [365 * int(instance['quote_date'].split('-')[0]) + 12 * int(instance['quote_date'].split('-')[1]) + int(instance['quote_date'].split('-')[2])] SUPPLIERS_LIST = ['S-0058', 'S-0013', 'S-0050', 'S-0011', 'S-0070', 'S-0104', 'S-0012', 'S-0068', 'S-0041', 'S-0023', 'S-0092', 'S-0095', 'S-0029', 'S-0051', 'S-0111', 'S-0064', 'S-0005', 'S-0096', 'S-0062', 'S-0004', 'S-0059', 'S-0031', 'S-0078', 'S-0106', 'S-0060', 'S-0090', 'S-0072', 'S-0105', 'S-0087', 'S-0080', 'S-0061', 'S-0108', 'S-0042', 'S-0027', 'S-0074', 'S-0081', 'S-0025', 'S-0024', 'S-0030', 'S-0022', 'S-0014', 'S-0054', 'S-0015', 'S-0008', 'S-0007', 'S-0009', 'S-0056', 'S-0026', 'S-0107', 'S-0066', 'S-0018', 'S-0109', 'S-0043', 'S-0046', 'S-0003', 'S-0006', 'S-0097'] def get_supplier(instance): if instance['supplier'] in SUPPLIERS_LIST: supplier_index = SUPPLIERS_LIST.index(instance['supplier']) result = [0] * supplier_index + [1] + [0] * (len(SUPPLIERS_LIST) - supplier_index - 1) else: result = [0] * len(SUPPLIERS_LIST) return result def get_assembly(instance): assembly_id = int(instance['tube_assembly_id'].split('-')[1]) result = [0] * assembly_id + [1] + [0] * (25000 - assembly_id - 1) return result def get_assembly_specs(instance, assembly_to_specs): result = [0] * 100 for spec in assembly_to_specs[instance['tube_assembly_id']]: result[int(spec.split('-')[1])] = 1 return result def to_sample(instance, additional_data): return (is_bracket_pricing(instance) + get_quantity(instance) + get_min_order_quantity(instance) + get_annual_usage(instance) + get_absolute_date(instance) + get_supplier(instance) + get_assembly_specs(instance, additional_data['assembly_to_specs'])) def to_interim_label(label): return math.log(label + 1) def to_final_label(interim_label): return math.exp(interim_label) - 1 def load_additional_data(): result = dict() assembly_to_specs = dict() with open('data/competition_data/specs.csv') as input_stream: header_line = input_stream.readline() for line in input_stream: tube_assembly_id = line.split(',')[0] specs = [] for spec in line.strip().split(',')[1:]: if spec != 'NA': specs.append(spec) assembly_to_specs[tube_assembly_id] = specs result['assembly_to_specs'] = assembly_to_specs return result if __name__ == '__main__': list_of_instances, list_of_labels = load_data() print(len(list_of_instances), len(list_of_labels)) print(list_of_instances[:3]) print(list_of_labels[:3])
[generate_response.py] import pickle import numpy import research class FinalModel(object): def __init__(self, model, to_sample, additional_data): self._model = model self._to_sample = to_sample self._additional_data = additional_data def process(self, instance): return self._model.predict(numpy.array(self._to_sample( instance, self._additional_data)).reshape(1, -1))[0] if __name__ == '__main__': with open('./data/model.mdl', 'rb') as input_stream: model = pickle.loads(input_stream.read()) additional_data = research.load_additional_data() final_model = FinalModel(model, research.to_sample, additional_data) print(final_model.process({'tube_assembly_id':'TA-00001', 'supplier':'S-0066', 'quote_date':'2013-06-23', 'annual_usage':'0', 'min_order_quantity':'0', 'bracket_pricing':'Yes', 'quantity':'1'}))
アルゴリズムをトレーニングするオブジェクトを説明するいくつかの機能が選択されました(これは退屈で、一見ITからは程遠い産業用パイプです)。 これらの兆候に基づいて、キー関数
to_sample()機能しますが、現在は次のようになっています
def to_sample(instance, additional_data): return (is_bracket_pricing(instance) + get_quantity(instance) + get_min_order_quantity(instance) + get_annual_usage(instance) + get_absolute_date(instance) + get_supplier(instance) + get_assembly_specs(instance, additional_data['assembly_to_specs']))
入力では、メイン
train_set.csvファイルに含まれるオブジェクト(インスタンス変数)の説明と、データセットの残りのファイルに基づいて生成された追加データのセットを取得し、出力は固定長の配列を返し、その後機械学習アルゴリズムによって入力に供給されます。
具体的なモデリングに関しては、特に進展はありません。Scikit-Learnパッケージのデフォルト設定とは異なる設定なしで、基本線形回帰がまだ使用されています。 それでも、当面は、アルゴリズム予測の品質を改善するために、機能のリストを徐々に増やしていきます。 前回、私たちは既に(非常に、本当にありふれた方法で)トレーニングデータ
train_set.csvメインファイルと補助データ
specs.csvファイルのすべての列を使用しました。 それで、おそらく、今度は、追加データを持つ他のファイルに注意を払うときです。 特に、各製品のコンポーネントを説明する
bill_of_materials.csvファイルの内容は有望に見えます。
標識のさらなる選択
$ head ./data/competition_data/bill_of_materials.csv tube_assembly_id,component_id_1,quantity_1,component_id_2,quantity_2,component_id_3,quantity_3,component_id_4,quantity_4,component_id_5,quantity_5,component_id_6,quantity_6,component_id_7,quantity_7,component_id_8,quantity_8 TA-00001,C-1622,2,C-1629,2,NA,NA,NA,NA,NA,NA,NA,NA,NA,NA,NA,NA TA-00002,C-1312,2,NA,NA,NA,NA,NA,NA,NA,NA,NA,NA,NA,NA,NA,NA TA-00003,C-1312,2,NA,NA,NA,NA,NA,NA,NA,NA,NA,NA,NA,NA,NA,NA TA-00004,C-1312,2,NA,NA,NA,NA,NA,NA,NA,NA,NA,NA,NA,NA,NA,NA TA-00005,C-1624,1,C-1631,1,C-1641,1,NA,NA,NA,NA,NA,NA,NA,NA,NA,NA TA-00006,C-1624,1,C-1631,1,C-1641,1,NA,NA,NA,NA,NA,NA,NA,NA,NA,NA TA-00007,C-1622,2,C-1629,2,NA,NA,NA,NA,NA,NA,NA,NA,NA,NA,NA,NA TA-00008,C-1312,2,NA,NA,NA,NA,NA,NA,NA,NA,NA,NA,NA,NA,NA,NA TA-00009,C-1625,2,C-1632,2,NA,NA,NA,NA,NA,NA,NA,NA,NA,NA,NA,NA
ご覧のとおり、ファイル形式は
specs.csv似てい
specs.csv 。 まず、実際に発生するコンポーネントの種類を確認しましょう。この情報を利用して、これらの補助データに基づいてどの機能を形成するのが妥当かを判断します。
>>> set_of_components = set() >>> with open('./data/competition_data/bill_of_materials.csv') as input_stream: ... header_line = input_stream.readline() ... for line in input_stream: ... for i in range(1, 16, 2): ... new_component = line.split(',')[i] ... set_of_components.add(new_component) ... >>> len(set_of_components) 2049 >>> sorted(set_of_components)[:10] ['9999', 'C-0001', 'C-0002', 'C-0003', 'C-0004', 'C-0005', 'C-0006', 'C-0007', 'C-0008', 'C-0009']
コンポーネントは非常に多くなることが判明したため、属性を標準的な方法で2000を超える要素の配列に拡張するという考えはあまり合理的ではないようです。 最も一般的な数十のオプションを使用してみてください。また、これらのオプションの数に関与する変数を、微調整の段階で最適化の調整パラメーターとして残してみましょう。
def load_additional_data(): result = dict() ... assembly_to_components = dict() component_to_popularity = dict() with open('./data/competition_data/bill_of_materials.csv') as input_stream: header_line = input_stream.readline() for line in input_stream: tube_assembly_id = line.split(',')[0] assembly_to_components[tube_assembly_id] = dict() for i in range(1, 16, 2): new_component = line.split(',')[i] if new_component != 'NA': quantity = int(line.split(',')[i + 1]) assembly_to_components[tube_assembly_id][new_component] = quantity if new_component in component_to_popularity: component_to_popularity[new_component] += 1 else: component_to_popularity[new_component] = 1 components_by_popularity = [value[0] for value in sorted( component_to_popularity.items(), key=operator.itemgetter(1, 0), reverse=True)] result['assembly_to_components'] = assembly_to_components result['components_by_popularity'] = components_by_popularity ... def get_assembly_components(instance, assembly_to_components, components_by_popularity, number_of_components): """ number_of_components: number of most popular components taken into account """ result = [0] * number_of_components for component in sorted(assembly_to_components[instance['tube_assembly_id']]): component_index = components_by_popularity.index(component) if component_index < number_of_components:
新しいサインなしでプログラムを実行して、検証の結果を思い出してください。
Mean Squared Error: 0.7754770419953809次に、新しい機能を追加します。
Mean Squared Error: 0.711158610883329ご覧のとおり、予測の品質が再び大幅に向上しています。 ちなみに、最初の数値調整パラメーター、つまり考慮に入れる最も一般的なコンポーネントの数を取得しました。 一般的な考慮事項に基づいて、パラメーターを増やすと、予測の品質が向上することを念頭に置いて、それを変えてみましょう-以前に使用されていない情報をますます考慮するからです。
100: 0.711158610883329200: 16433833.592963027150: 0.7110152873760721170: 19183113.422557358160: 0.7107685953594116165: 0.7119011633609398168: 24813512.02303443166: 0.7119603793730067167: 0.7119604617354474値が168を超えると、どのような大惨事が発生するかを言うのは依然として困難です。そのため、予測の品質が急激かつ急激に低下します。 それ以外の場合、大きな変更はありません。 私たちの良心をクリアするために、変数パラメーターの減少によって予測の質がどのように変化するかを見てみましょう。
80: 0.711631137346376650: 0.721156084134771230: 0.754857014803288770: 0.7121518708790175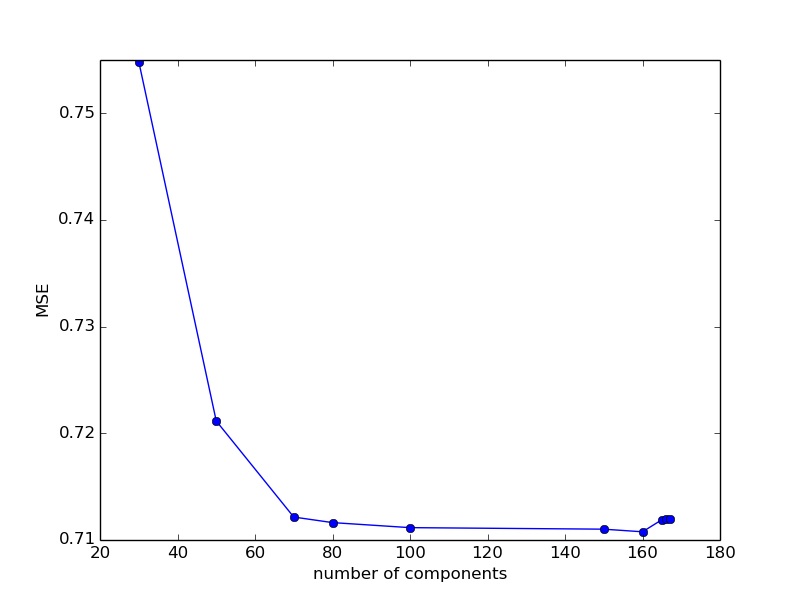
コンポーネントの数が減少するにつれて誤差が増加し、80〜160の値ではほぼ一定のままであることがわかります。 ここでは、パラメーターを100のままにしておきます。
ご覧のとおり、新しい機能の追加により、検証が大幅に改善されています。 この種の実験をさらにいくつか行い、その後、トレーニングモデルとそのトレーニングパラメーターのバリエーションに進みます。 より複雑な配置を検討します
が、データファイルの
説明から判断すると、キーファイルは
tube.csvです。
$ head data/competition_data/tube.csv tube_assembly_id,material_id,diameter,wall,length,num_bends,bend_radius,end_a_1x,end_a_2x,end_x_1x,end_x_2x,end_a,end_x,num_boss,num_bracket,other TA-00001,SP-0035,12.7,1.65,164,5,38.1,N,N,N,N,EF-003,EF-003,0,0,0 TA-00002,SP-0019,6.35,0.71,137,8,19.05,N,N,N,N,EF-008,EF-008,0,0,0 TA-00003,SP-0019,6.35,0.71,127,7,19.05,N,N,N,N,EF-008,EF-008,0,0,0 TA-00004,SP-0019,6.35,0.71,137,9,19.05,N,N,N,N,EF-008,EF-008,0,0,0 TA-00005,SP-0029,19.05,1.24,109,4,50.8,N,N,N,N,EF-003,EF-003,0,0,0 TA-00006,SP-0029,19.05,1.24,79,4,50.8,N,N,N,N,EF-003,EF-003,0,0,0 TA-00007,SP-0035,12.7,1.65,202,5,38.1,N,N,N,N,EF-003,EF-003,0,0,0 TA-00008,SP-0039,6.35,0.71,174,6,19.05,N,N,N,N,EF-008,EF-008,0,0,0 TA-00009,SP-0029,25.4,1.65,135,4,63.5,N,N,N,N,EF-003,EF-003,0,0,0
「material_id」列の内容には、
specs.csv指定された値が
specs.csvとして
specs.csvられていることに
specs.csvして
specs.csv 。 これが何を意味するかを言うのは依然として困難であり、specs.csvの最初の20行に含まれるSP-xyzt型のいくつかの値を検索しても何も見つかりませんが、念のためこの機能を覚えておいてください。 また、コンテストの説明に基づいて、列に示されている素材と
bill_of_materials.csv示されている素材の実際の違いを理解することは困難
bill_of_materials.csv 。 ただし、当面は、このような洗練された質問に悩まされることはなく、通常の方法で可能なオプションの数を分析し、その値を(できれば)アルゴリズムに役立つ記号に変換しようとします。
>>> set_of_materials = set() >>> with open('./data/competition_data/tube.csv') as input_stream: ... header_line = input_stream.readline() ... for line in input_stream: ... new_material = line.split(',')[1] ... set_of_materials.add(new_material) ... >>> len(set_of_materials) 20 >>> set_of_materials {'SP-0034', 'SP-0037', 'SP-0039', 'SP-0030', 'SP-0029', 'NA', 'SP-0046', 'SP-0028', 'SP-0031', 'SP-0032', 'SP-0033', 'SP-0019', 'SP-0048', 'SP-0008', 'SP-0045', 'SP-0035', 'SP-0044', 'SP-0036', 'SP-0041', 'SP-0038'}
かなり多くのオプションが明らかになったため、標準のカテゴリ属性を追加することをreallyすることはできません。 これを行うには、最初に
assembly_to_material辞書をロードして
load_additional_data()関数を
load_additional_data()ます。
assembly_to_material = dict() with open('./data/competition_data/tube.csv') as input_stream: header_line = input_stream.readline() for line in input_stream: tube_assembly_id = line.split(',')[0] material_id = line.split(',')[1] assembly_to_material[tube_assembly_id] = material_id result['assembly_to_material'] = assembly_to_material
そして、既存の関数の1つと同様に記述するときに使用します。
MATERIALS_LIST = ['NA', 'SP-0008', 'SP-0019', 'SP-0028', 'SP-0029', 'SP-0030', 'SP-0031', 'SP-0032', 'SP-0033', 'SP-0034', 'SP-0035', 'SP-0036', 'SP-0037', 'SP-0038', 'SP-0039', 'SP-0041', 'SP-0044', 'SP-0045', 'SP-0046', 'SP-0048'] def get_material(instance, assembly_to_material): material = assembly_to_material[instance['tube_assembly_id']] if material in MATERIALS_LIST: material_index = MATERIALS_LIST.index(material) result = [0] * material_index + [1] + [0] * (len(MATERIALS_LIST) - material_index - 1) else: result = [0] * len(MATERIALS_LIST) return result
Mean Squared Error: 0.7187098083419174残念ながら、この機能は既存の結果(約0.711)の改善には役立ちませんでした。 しかし、それは問題ではありません-私たちの仕事が無駄にならず、より複雑なモデルのセットアップに役立つことを願うことができます。 同じ
tube.csvファイルの次の列は、パイプの直径を
tube.csvます。 オブジェクトのこのプロパティは
量的と呼ばれ、最も単純で最も自然な方法で、つまり値を取ることにより、符号に変換されます。 もちろん、場合によっては、何らかの方法で正規化または変更することが有用かもしれませんが、最初の試みでは、それなしで行うことができます。 この属性に一致するコードを記述することで、これが身近な方法になりました。
def get_diameter(instance, assembly_to_diameter): return [assembly_to_diameter[instance['tube_assembly_id']]]
to_sample()関数に追加すると、検証サンプルのモデル予測の品質がさらに向上します。
Mean Squared Error: 0.6968043166687439ご覧のとおり、検証サンプルで新機能と新機能を簡単に抽出し、モデル予測の品質をテストすることで、品質メトリックが引き続き改善されています。 ただし、一方では、新しい機能からの成長は既にそれほど大きくありません(また、マイナスの場合があります-そして、材料の前の例のように、対応する機能を拒否する必要があります)、他方では、競争や作業ではなくトレーニングプロジェクトがありますそのため、しばらくの間機能の選択を終了し、アルゴリズムの選択とパラメーターの最適化の問題に進みます。
モデルが異なります
現在の機能セットのフレームワーク内で、最適に近い機械学習モデルと対応するハイパーパラメーターセットを見つけようとします。 さまざまなモデルをテストすることから始めましょう。 まず、単純な線形回帰を、使いやすいKerasパッケージのファッショナブルなニューラルネットワークに置き換えてみましょう。
from keras.models import Sequential from keras.layers import Dense from keras.optimizers import SGD model = Sequential() model.add(Dense(units=30, activation='tanh', input_dim=len(list_of_samples[0]))) model.add(Dense(units=1, activation='linear')) optimizer = SGD(lr=0.1) model.compile(loss='mean_squared_error', optimizer=optimizer, metrics=['accuracy'])
これは、レイヤー内のニューロンの数が30、
learning_rateが0.1、アクティベーション関数
tanh完全に接続されたネットワークアーキテクチャに対応しています。 出力層では、数値パラメーターを予測するため、関数は線形であり、シグモイドのこの変動ではないことに注意してください。
Mean Squared Error: nanエラーは非常に大きく、(かなり大きい)numpy-ev intに収まらないことが判明しました。 別のレイヤーを追加してみましょう。
from keras.models import Sequential from keras.layers import Dense from keras.optimizers import SGD model = Sequential() model.add(Dense(units=30, activation='tanh', input_dim=len(list_of_samples[0]))) model.add(Dense(units=20, activation='tanh', input_dim=len(list_of_samples[0]))) model.add(Dense(units=1, activation='linear')) optimizer = SGD(lr=0.1) model.compile(loss='mean_squared_error', optimizer=optimizer, metrics=['accuracy'])
Mean Squared Error: nan繰り返しますが、良い結果は機能しませんでした。 残念ですが、どうやら、ニューラルネットワーク-モデルは便利で優れていますが、私たちのタスクには適していません。 ただし、ニューラルネットワークタイプのモデルを使用して良い結果を得る方法を誰かが知っている場合は、コメント内のコードへのリンクを待っているので、より保守的なアプローチに切り替えます。 たとえば、回帰問題を解決するための標準アルゴリズムの1つは勾配ブースティングです。 使ってみよう。
model = GradientBoostingRegressor()
Mean Squared Error: 0.44000911792278125宣伝されたニューラルネットワークの耳をつんざくような失敗の後、間違いなく私たちの精神を高める大きな進歩は明らかです。 ここでは、もちろん、RidgeRegressionのような他のアルゴリズムを試すことができますが、一般的に、著者は勾配ブースティングがそのようなタスクに適していること、ニューラルネットワークが本当に悪いこと、そして残りのモデルが多かれ少なかれだと知っていたので、説明しませんすべての可能なオプション、およびそれらの最適なハイパーパラメーター、つまりブーストを最適化します。
ここにあるScikit-Learnライブラリ専用のサイトの対応するページに移動
するか、単にコンソールにヘルプ(GradientBoostingRegressor)と入力すると、このアルゴリズムの実装には次のチューニングパラメーターとそのデフォルト値のセットがあることがわかります。
loss='ls'learning_rate=0.1n_estimators=100subsample=1.0criterion='friedman_mse'min_samples_split=2min_samples_leaf=1min_weight_fraction_leaf=0.0max_depth=3min_impurity_decrease=0.0min_impurity_split=Noneinit=Nonerandom_state=Nonemax_features=Nonealpha=0.9verbose=0max_leaf_nodes=Nonewarm_start=Falsepresort='auto'それらを1つずつ分析して、それらを変更してみましょう。一見すると、その変動は予測の品質を改善するのに役立ちます。
| loss : {'ls', 'lad', 'huber', 'quantile'}, optional (default='ls') | loss function to be optimized. 'ls' refers to least squares | regression. 'lad' (least absolute deviation) is a highly robust | loss function solely based on order information of the input | variables. 'huber' is a combination of the two. 'quantile' | allows quantile regression (use `alpha` to specify the quantile).
最適化する損失関数。 問題の再定式化後(ラベルから対数を取得し、それに応じてLMSEの代わりにMSEを最適化するという点で)、デフォルトのパラメーターはタスクに対応しているように見えます。 そのままにしておきます。
| learning_rate : float, optional (default=0.1) | learning rate shrinks the contribution of each tree by `learning_rate`. | There is a trade-off between learning_rate and n_estimators.
多くのタスクで、構成する重要なパラメーター。 他の値で何が起こるか見てみましょう。
MODEL_SETTINGS = { 'model_name':'GradientBoostingRegressor', 'learning_rate':0.100} ... model = GradientBoostingRegressor(learning_rate=MODEL_SETTINGS['learning_rate'])
ハイパーパラメーターの単純で明示的な宣言は、このようなやや精巧な形式で記述されているため、将来的には、スクリプトのヘッダー内のモデルパラメーター(およびモデル自体)を変更すると便利です。
Mean Squared Error: 0.44002379237806705 MODEL_SETTINGS = { 'model_name':'GradientBoostingRegressor', 'learning_rate':0.200}
Mean Squared Error: 0.41423518862618164ええ、
learning_rateが増加する
learning_rate 、品質メトリックが大幅に改善されます。 このパラメーターを同じ方向に変更し続けてみましょう。
MODEL_SETTINGS = { 'model_name':'GradientBoostingRegressor', 'learning_rate':0.300}
Mean Squared Error: 0.4051555356961356まだ増やしましょう
MODEL_SETTINGS = { 'model_name':'GradientBoostingRegressor', 'learning_rate':0.500}
Mean Squared Error: 0.39668129369369115その他
MODEL_SETTINGS = { 'model_name':'GradientBoostingRegressor', 'learning_rate':1.000}
Mean Squared Error: 0.434184026080522次のパラメータの増加により、ターゲットメトリックは悪化しました。 中間値の中から何かを探してみましょう。
MODEL_SETTINGS = { 'model_name':'GradientBoostingRegressor', 'learning_rate':0.700}
Mean Squared Error: 0.39998809063954305 MODEL_SETTINGS = { 'model_name':'GradientBoostingRegressor', 'learning_rate':0.600}
Mean Squared Error: 0.4032676539076024実験で得られたデータはすでに非常に紛らわしいので、それらを表にまとめて適切なグラフを描きましょう(個人的には、私は通常、このようなグラフを見ていないので、精神的な構造に制限されますが、これは教育目的に役立ちます)。
| learning_rate | MSE |
|---|
| 0.100 | 0.4400 |
| 0.200 | 0.4142 |
| 0.300 | 0.4051 |
| 0.500 | 0.3966 |
| 0.600 | 0.4032 |
| 0.700 | 0.3999 |
| 1,000 | 0.4341 |

一見すると、
learning_rate率が0.100から0.500に減少することで品質メトリックが改善し、約0.700まで比較的安定したままになり、その後悪化するように見えます。 さらに多くの実験でこの仮説をテストします。
MODEL_SETTINGS = { 'model_name':'GradientBoostingRegressor', 'learning_rate':0.400}
Mean Squared Error: 0.40129637223972486 MODEL_SETTINGS = { 'model_name': 'GradientBoostingRegressor', 'learning_rate': 0.800}
Mean Squared Error: 0.4253214442400451 MODEL_SETTINGS = { 'model_name': 'GradientBoostingRegressor', 'learning_rate': 0.550}
Mean Squared Error: 0.39587242367884334 MODEL_SETTINGS = { 'model_name': 'GradientBoostingRegressor', 'learning_rate': 0.650}
Mean Squared Error: 0.40041838873950636| learning_rate | MSE |
|---|
| 0.100 | 0.4400 |
| 0.200 | 0.4142 |
| 0.300 | 0.4051 |
| 0.400 | 0.4012 |
| 0.500 | 0.3966 |
| 0.550 | 0.3958 |
| 0.600 | 0.4032 |
| 0.650 | 0.4004 |
| 0.700 | 0.3999 |
| 0.800 | 0.4253 |
| 1,000 | 0.4341 |

最適値は0.500から0.550の範囲にあり、いずれかの方向の変化は、概して、モデルのパラメーターまたは属性リストの他の可能な変化と比較して、最終メトリックにほとんど反映されていないようです。 learning_rateを0.550に修正し、モデルの他のパラメーターに注意を払います。
ところで、同様の場合、ハイパーパラメーターの1つまたは別のセットが正しく選択されるようにするために、多くのアルゴリズムで使用可能なrandom_stateパラメーターを変更するか、サンプルをそれらの要素の数を維持しながらトレーニングと検証に分割することも役立ちます。 これにより、ハイパーパラメーター設定と検証サンプルの予測の質との間に明確なパターンがない場合に、アルゴリズムの実際の有効性に関する詳細情報を収集できます。
| n_estimators:int(デフォルト= 100)
| 実行するブースティングステージの数。 勾配ブースティング
| 過剰適合に対してかなり堅牢であるため、通常は多数
| パフォーマンスが向上します。
勾配ブースティングモデルを学習する際の特定の「ブースティングステージ」の数。 正直に言うと、著者はアルゴリズムの正式な定義で彼らがどのような役割を果たしているかを既に忘れていますが、それを取り上げてこのパラメーターをテストしましょう。 ところで、モデルトレーニングに費やした時間を正確に特定し始めます。
import time MODEL_SETTINGS = { 'model_name':'GradientBoostingRegressor', 'learning_rate':0.550, 'n_estimators':100} model = GradientBoostingRegressor(learning_rate=MODEL_SETTINGS['learning_rate'], n_estimators=MODEL_SETTINGS['n_estimators']) time_start = time.time() model.fit(numpy.array(train_samples), numpy.array(train_labels)) print('Time spent: {0}'.format(time.time() - time_start)) print('MODEL_SETTINGS = {{\n {0}\n {1}\n {2}}}' .format(MODEL_SETTINGS['model_name'], MODEL_SETTINGS['learning_rate'], MODEL_SETTINGS['n_estimators']))
MODEL_SETTINGS = { 'model_name': GradientBoostingRegressor, 'learning_rate': 0.55, 'n_estimators': 100}
Time spent: 71.83099746704102Mean Squared Error: 0.39622103688045596 MODEL_SETTINGS = { 'model_name': GradientBoostingRegressor 'learning_rate': 0.55 'n_estimators': 200}
Time spent: 141.9290111064911Mean Squared Error: 0.40527237378150016ご覧のとおり、トレーニングに費やされる時間は大幅に増加し、品質指標は悪化しているだけです。念のため、もう一度パラメーターを増やしてみてください。 MODEL_SETTINGS = { 'model_name': GradientBoostingRegressor 'learning_rate': 0.55 'n_estimators': 300}
Time spent: 204.2548701763153Mean Squared Error: 0.4027642069054909難しいですが、明確ではありません。すべてをロールバックして、他の成長ポイントを探してみましょう。| max_depth:整数、オプション(デフォルト= 3)| 個々の回帰推定の最大深度。最大| depthは、ツリー内のノードの数を制限します。このパラメーターを調整する| 最高のパフォーマンスを得るために。最適な値は相互作用に依存します| 入力変数の。 MODEL_SETTINGS = { 'model_name': GradientBoostingRegressor 'learning_rate': 0.55 'n_estimators': 100 'max_depth': 3}
Time spent: 66.88031792640686Mean Squared Error: 0.39713231957974565 MODEL_SETTINGS = { 'model_name': GradientBoostingRegressor 'learning_rate': 0.55 'n_estimators': 100 'max_depth': 4}
Time spent: 86.24338245391846Mean Squared Error: 0.40575622943301354 MODEL_SETTINGS = { 'model_name': GradientBoostingRegressor 'learning_rate': 0.55 'n_estimators': 100 'max_depth': 2}
Time spent: 45.39022421836853Mean Squared Error: 0.41356622455188463残念ながら、それも助けにはなりません。元の値に戻って先に進みます。|基準:文字列、オプション(デフォルト= "friedman_mse")|スプリットの品質を測定する機能。サポートされている基準|は改善された平均二乗誤差の「friedman_mse」です。フリードマンによるスコア、「mse」は平均二乗誤差、「mae」は|平均絶対誤差。 「friedman_mse」のデフォルト値は||でより良い近似を提供できるため、一般的に最適です。いくつかのケース。このパラメーターの変更がモデルの改善に役立ったことを覚えていません。Vorontsovが講演で、分離基準を実際に変更しても最終モデルの品質には影響しないと言ったので、スキップして先に進みます。| min_samples_split:int、float、オプション(デフォルト= 2)| 内部ノードを分割するために必要なサンプルの最小数:|| -intの場合、 `min_samples_split`を最小数と見なします。| -フロートの場合、 `min_samples_split`はパーセンテージで、| `ceil(min_samples_split * n_samples)`は最小値です。各スプリットのサンプル数。|| ... versionchanged :: 0.18| パーセンテージのフロート値を追加しました。トレーニング中に特定の頂点でツリーを構築し続けるために必要なサンプルの最小数。変更してみましょう。 MODEL_SETTINGS = { 'model_name': GradientBoostingRegressor 'learning_rate': 0.55 'n_estimators': 100 'max_depth': 3 'min_samples_split': 2 } <source> <code>Time spent: 66.22262406349182</code> <code>Mean Squared Error: 0.39721489877049687</code> - , , . . <source lang="python"> MODEL_SETTINGS = { 'model_name': GradientBoostingRegressor, 'learning_rate': 0.55, 'n_estimators': 100, 'max_depth': 3 , 'min_samples_split': 3 }
Time spent: 66.18473935127258Mean Squared Error: 0.39493122173406714 MODEL_SETTINGS = { 'model_name': GradientBoostingRegressor 'learning_rate': 0.55 'n_estimators': 100 'max_depth': 3 'min_samples_split': 8 }
Time spent: 66.7643404006958Mean Squared Error: 0.3982469042761572進行は終わったので、はっきりと始まりませんでした。完全を期すため、中間値4を使用してみてください。 MODEL_SETTINGS = { 'model_name': GradientBoostingRegressor, 'learning_rate': 0.55, 'n_estimators': 100, 'max_depth': 3, 'min_samples_split': 4 }
Time spent: 66.75952744483948Mean Squared Error: 0.39451862900585913の場合よりもかなり優れていますが、それでも、トレーニング時間に違いがないため、この値のままにしておきます。| min_samples_leaf:int、float、オプション(デフォルト= 1)|リーフノードにあるために必要なサンプルの最小数:|| -intの場合、 `min_samples_leaf`を最小数と見なします。| -フロートの場合、 `min_samples_leaf`はパーセンテージで、| `ceil(min_samples_leaf * n_samples)`は最小値です。各ノードのサンプル数。|| ... versionchanged :: 0.18|パーセンテージのフロート値を追加しました。トレーニング後にツリーの葉にできるサンプルの最小数。このパラメーターを大きくすると、トレーニングサンプルの予測の品質が低下します(値が小さいほど、アンサンブルを構成するツリーはトレーニングサンプルの特定の各例により適合しているため)。また、運が良ければ、検証サンプルの品質が向上します。つまり、少なくとも理論的には、再訓練と戦うのに役立ちます。 MODEL_SETTINGS = { 'model_name': GradientBoostingRegressor, 'learning_rate': 0.55, 'n_estimators': 100, 'max_depth': 3, 'min_samples_split': 4 'min_samples_leaf': 1}
Time spent: 68.58824563026428Mean Squared Error: 0.39465027476703846「デフォルト」パラメータを代入するときの予測は、前の実験の値とほぼ同じです。これは、すべてが正常に機能していることを意味します。これまでの簡単な検証手順では、アルゴリズムの予測の品質に真に対応する値が返され、パラメーターの開始値を混同しませんでした。 MODEL_SETTINGS = { 'model_name': GradientBoostingRegressor, 'learning_rate': 0.55, 'n_estimators': 100, 'max_depth': 3, 'min_samples_split': 4 'min_samples_leaf': 2}
Time spent: 68.03447198867798Mean Squared Error: 0.39707533548242パラメーターが1から2に増加すると、アルゴリズムの品質メトリックの低下が見られます。それでも、もう一度増やしてみてください。 MODEL_SETTINGS = { 'model_name': GradientBoostingRegressor, 'learning_rate': 0.55, 'n_estimators': 100, 'max_depth': 3, 'min_samples_split': 4, 'min_samples_leaf': 3, 'random_seed': 0}
Time spent: 66.98832631111145Mean Squared Error: 0.39419555554861274ターゲットメトリックを悪化させた後、パラメータを連続して2回増やすと、その改善が見られ、元の値を超えることさえ疑わしいです。もう少し高く、現在の検証手順が予測の質の少なくとも4桁までの適切な評価を提供するという事実を支持する強力な証拠を受け取りました。random_seedパラメーターが変更されたときに何が起こるかを確認しましょう。 MODEL_SETTINGS = { 'model_name': GradientBoostingRegressor, 'learning_rate': 0.55, 'n_estimators': 100, 'max_depth': 3, 'min_samples_split': 4, 'min_samples_leaf': 3, 'random_seed': 1}
Time spent: 67.16857171058655Mean Squared Error: 0.39483997966302 MODEL_SETTINGS = { 'model_name': GradientBoostingRegressor, 'learning_rate': 0.55, 'n_estimators': 100, 'max_depth': 3, 'min_samples_split': 4 'min_samples_leaf': 3, 'random_seed': 2}
Time spent: 66.11015605926514Mean Squared Error: 0.39492203941997045少なくとも上記の小数点以下4桁まで、検証手順は実際にモデルの適切な評価を提供するようです。したがって、次の「良心を明らかにする」テストは、驚くべきことに、ハイパーパラメーターの値に応じて非単調に品質を確認するのに役立ちました。再び増やすことは価値があります。 MODEL_SETTINGS = { 'model_name': GradientBoostingRegressor, 'learning_rate': 0.55, 'n_estimators': 100, 'max_depth': 3, 'min_samples_split': 4 'min_samples_leaf': 4 , 'random_seed': 0}
Time spent: 66.96864414215088Mean Squared Error: 0.39725274882841366再び悪化します。たぶん事実は、いくつかの魔法の理由で、パラメーターの値が偶数の場合、予測の品質が奇数のものよりもわずかに悪いということですか?誰が知っている。 MODEL_SETTINGS = { 'model_name': GradientBoostingRegressor, 'learning_rate': 0.55, 'n_estimators': 100, 'max_depth': 3, 'min_samples_split': 4 'min_samples_leaf': 5 , 'random_seed': 0}
Time spent: 66.33412432670593Mean Squared Error: 0.39348528600652666 MODEL_SETTINGS = { 'model_name': GradientBoostingRegressor, 'learning_rate': 0.55, 'n_estimators': 100, 'max_depth': 3, 'min_samples_split': 4 'min_samples_leaf': 5 , 'random_seed': 1}
Time spent: 66.22624254226685Mean Squared Error: 0.3935675331843957品質が少し向上しました。そして、偶数の値を持つ最悪の予測品質に関する「仮説」は、別の確認を受けました。おそらくこれはそのような事故ではありません。 MODEL_SETTINGS = { 'model_name': GradientBoostingRegressor, 'learning_rate': 0.55, 'n_estimators': 100, 'max_depth': 3, 'min_samples_split': 4, 'min_samples_leaf': 6 , 'random_seed': 0}
Time spent: 66.88769054412842Mean Squared Error: 0.38855940004423717それでも、5から6に切り替えると、品質はわずかに向上しました。スペースを節約するために、実験の完全なログをスキップし、すぐに結果をテーブルに転送して、適切なスケジュールを生成します。| min_samples_leaf | MSE | 過ごした時間 |
|---|
| 1 | 0.3946 | 68.58 |
| 2 | 0.3970 | 68.03 |
| 3 | 0.3941 | 66.98 |
| 4 | 0.3972 | 66.96 |
| 5 | 0.3934 | 66.33 |
| 6 | 0.3885 | 66.88 |
| 7 | 0.3895 | 65.22 |
| 8 | 0.3903 | 65.89 |
| 9 | 0.3926 | 66.31 |
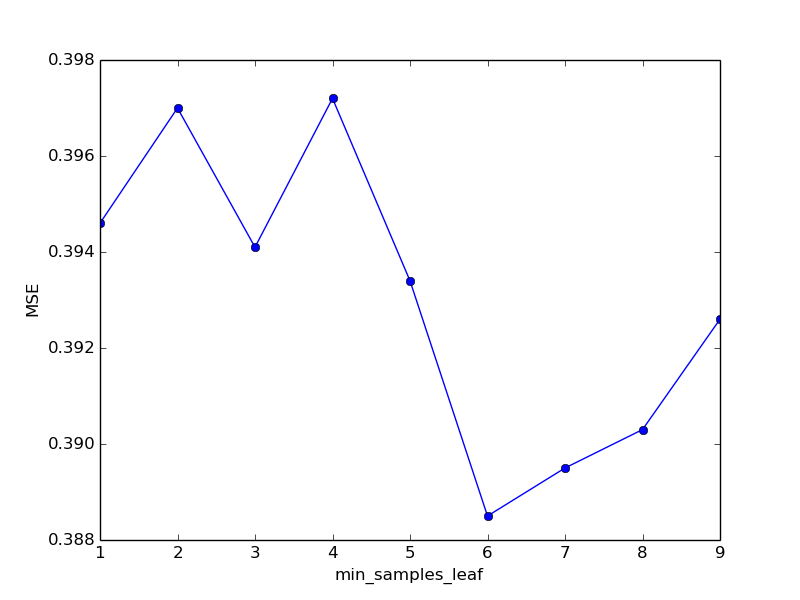 取得した検証結果に高い信頼性があるため、min_samples_leafの最適値は6であると想定できます。次のパラメーターを使用した実験に進みましょう。| min_weight_fraction_leaf:float、オプション(デフォルト= 0)|リーフノードにある必要がある(すべての入力サンプルの)重みの合計の最小重み付き割合。サンプルを持っています| sample_weightが指定されていない場合、等しい重み。シートを形成するために必要な例の最小部分。デフォルトでは、それらの数はゼロです。つまり、制限は設定されていません。理論的には、このパラメーターの値を大きくすると、mean_samples_leafパラメーターのように再トレーニングが防止されます。
取得した検証結果に高い信頼性があるため、min_samples_leafの最適値は6であると想定できます。次のパラメーターを使用した実験に進みましょう。| min_weight_fraction_leaf:float、オプション(デフォルト= 0)|リーフノードにある必要がある(すべての入力サンプルの)重みの合計の最小重み付き割合。サンプルを持っています| sample_weightが指定されていない場合、等しい重み。シートを形成するために必要な例の最小部分。デフォルトでは、それらの数はゼロです。つまり、制限は設定されていません。理論的には、このパラメーターの値を大きくすると、mean_samples_leafパラメーターのように再トレーニングが防止されます。 MODEL_SETTINGS = { 'model_name': GradientBoostingRegressor, 'learning_rate': 0.55, 'n_estimators': 100, 'max_depth': 3, 'min_samples_split': 4, 'min_samples_leaf': 6 , 'random_seed': 0, 'min_weight_fraction_leaf': 0.01}
Time spent: 68.06336092948914Mean Squared Error: 0.41160143391833687残念ながら、予測の質は悪化しています。しかし、私たちはあまりにも重要視しすぎたのでしょうか? MODEL_SETTINGS = { 'model_name': GradientBoostingRegressor, 'learning_rate': 0.55, 'n_estimators': 100, 'max_depth': 3, 'min_samples_split': 4, 'min_samples_leaf': 6 , 'random_seed': 0, 'min_weight_fraction_leaf': 0.001}
Time spent: 67.03254532814026Mean Squared Error: 0.39262469473669265繰り返しますが、減少は私たちを助けませんでした。一般的に、このパラメーターの説明から判断すると、固定サイズをサンプリングする場合、指定されたmin_samples_leafまたは指定されたmin_weight_fraction_leafのいずれかの制限が適用されます。そのままにして、次へ進んでください。|サブサンプル:フロート、オプション(デフォルト= 1.0)|個々のベースの適合に使用されるサンプルの割合|学習者。 1.0より小さい場合、これは確率的勾配になります。ブースティング「subsample」はパラメーター「n_estimators」と対話します。| 「サブサンプル<1.0」を選択すると、分散が減少します。バイアスの増加。 MODEL_SETTINGS = { 'model_name': GradientBoostingRegressor, 'learning_rate': 0.55, 'n_estimators': 100, 'max_depth': 3, 'min_samples_split': 4, 'min_samples_leaf': 6, 'random_seed': 0, 'min_weight_fraction_leaf': 0.0, 'subsample': 0.9}
Time spent: 155.24894833564758Mean Squared Error: 0.39231319253775626単にパラメータを変更するだけではもはや役に立たないように見えます(そして、ほとんど役に立たないものと想定できます)。このステップを完了するために、リクエストを処理する最後の時間クラスを使用してkaggleの送信を生成しましょう。もちろん、kaggleで問題を解決するとき、オプションは通常よりシンプルに使用されますが、実際のアプリケーションで発生する状況をシミュレートし、前回書いたクラスをテストするために、追加のコードを書くのに少し時間を費やすことができます。予測ファイルを生成する
ネタバレの下にはgenerate_response.pyスクリプトの変更があります。スクリプト修正[generate_response.py]
import pickle import numpy import research class FinalModel(object): def __init__(self, model, to_sample, additional_data): self._model = model self._to_sample = to_sample self._additional_data = additional_data def process(self, instance): return self._model.predict(numpy.array(self._to_sample( instance, self._additional_data)).reshape(1, -1))[0] if __name__ == '__main__': with open('./data/model.mdl', 'rb') as input_stream: model = pickle.loads(input_stream.read()) additional_data = research.load_additional_data() final_model = FinalModel(model, research.to_sample, additional_data)
スクリプトは、入力データとして、スクリプトによって生成されたモデルと、コンテストの主催者によって提供されたアーカイブにあるresearch.pyテストデータを含むファイルを使用します。出口で彼は、ファイルgereriruet output.csv。ファイル内の予測の形成に関連する変更がないことは、トレーニングおよびサービングパイプラインの柔軟性を示しています。多くの新機能をピックアップし、モデルを変更し、以前は使用されていなかった新しいデータファイルを使用しましたが、モデルのアプリケーションに関連するコードの部分は基本的に変更されていません。test_set.csvgenerate_response.pykaggleコンペティションはすでに終了していますが、プラットフォームの評価が検証の期待にどのように一致するかをここで確認できます。 結果は、一見、元気づけられます-予測の品質は検証よりもさらに高いことが判明しました。ただし、一方では、パブリックリーダーボードの結果は検証の結果よりも非常に高く、他方では、全体的な順位における(競争が終了した瞬間に比べて)私たちの位置はまだ高くありません。ただし、これらの問題の両方に対する解決策は別の機会にお任せします。
結果は、一見、元気づけられます-予測の品質は検証よりもさらに高いことが判明しました。ただし、一方では、パブリックリーダーボードの結果は検証の結果よりも非常に高く、他方では、全体的な順位における(競争が終了した瞬間に比べて)私たちの位置はまだ高くありません。ただし、これらの問題の両方に対する解決策は別の機会にお任せします。おわりに
そこで、予測アルゴリズムを最適化し、さまざまなモデルを試し、そのような広く宣伝されているニューラルネットワークがタスクにあまり適していないことを発見し、ハイパーパラメーターの選択を試し、最終的にkaggleの最初の予測ファイルを作成しました。1つの記事についてはそれほどではありません。またお会いしましょう。少しオフトピック, , . HR- . , , , , ( ). , , . , , , , - , . , . ( — ) , , , .