著名なコミュニティへの挨拶。
最近、私は構文解析のトピックに注意を払い(自分の知識とスキルも向上させることを目的としています)、ほとんどすべてのコンパイラーコースは数学的形式から始まり、学生による比較的高いレベルのトレーニングが必要であるという印象を受けました。 または、たとえば、古典的なドラゴンブックのように、正式な数学表記が大量に使用されています。
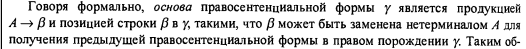
それは習慣から怖がらせることができます。 いいえ、ある時点から正式な録音が便利になり、必要になりますが、「指で」「何が問題なのか」と説明したい「通りの人」にとっては難しいかもしれません。 そして、「LLとLR分析とは何か、それらの違いは何か」という質問は、プログラマーによってよく尋ねられます(すべてのプログラマーが私のようにコンピューターサイエンスの正式な教育を受けているわけではなく、全員がそこでコンパイラーコースを受講したわけではないためです) )
アプローチは私にとってより身近であり、最初に問題を取り上げて解決しようとすると、解決の過程で最初に原理の直感的な理解を発展させ、次にこの理解のための数学的形式を作成します。 したがって、この記事では、上向き解析(ボトムアップ解析、別名LR)の基礎となるアイデアを非常に簡単な例で示したいと思います。 さらに単純化するために、加算、乗算、および括弧演算子のみをサポートする算術式を計算します(負の数と単項マイナスのサポートで例を複雑にしないため)。
タスクに直接進む前に、解析のトピックに関する一般的な考慮事項をいくつか書きます。
解析はコンピューターサイエンスの基本的な概念の1つであり(その部分では、正式な言語、実際のプログラミング言語について)、ほとんどすべてのプログラマーが遅かれ早かれこのトピックを理解する必要に迫られています。 特に、彼が遅かれ早かれ実装したいと思うある種のミニ言語のある種のミニ通訳を書き始めたときは特にそうです。 さらに、プログラマーはインタープリターを構築していることに気付かないこともありますが、ある種の「ルール」、「アクション」、または「構成」を記述するための「便利なフォーマット」を思いついたと思うかもしれません。読んでください。」 私の意見では、汎用言語を使用してDSL(ドメイン固有言語)インタープリターを作成する場合、これは言語指向プログラミングの概念につながる自然なプロセスであり、このDSLはプロジェクトでますます使用されています。このサブジェクトエリアは、DSLを使用して記述する方が便利であることがわかります。
したがって、構文解析は、それなしではインタープリターを構築できないことが重要です。 また、算術式を計算するタスクはおそらく最も単純なタスクの1つであり、そのソリューションでは既に解析が必要です。 したがって、通常、この複雑なトピックに慣れるのは、ほとんどの場合このトピックから始まります。
算術式はどのように計算できますか? これを逆ポーランド記法に変換してスタック上で計算し、再帰降下法を使用して計算するアナライザーを作成し、シャンティングヤードアルゴリズムを使用し、パーサージェネレーター(ANTLRまたはbison)を使用して、パーサーが作成し、計算することができますその中の表現。
しかし、ANTLRやbisonなどのツールを使用すると、ある種の魔法を始めたような気がします。コンパイルした文法からパーサーが生成され、それを使用すると、その仕組みがわかりません。 いくつかのより高い力が彼を上回り、あなたの理解の能力を超えているかのようでした。 さらに、これらのツールを使用するとき、私たちは常に解析したい言語の文法から踊り始め、文法をコンパイルするタスク自体はそれほど単純ではありません。 あなたはそれが何であるか、どのように機能するか、左再帰を排除する方法(そしてそれが一般的に何であるか)、LRのいくつかの文法がLLで動作しないかもしれない理由、そしてそれらを必要に応じて書き直す方法を理解する必要があります これは、特に「文法」(および「生産」、「終端記号」、「非終端記号」、「法的感情」などの概念)などの概念が概念装置に含まれていない場合、すぐに困難になる可能性があります(「アクティブな語彙」)、たとえば算術式の同じ計算機を作成しようとしているプログラマーの。 したがって、上向き解析の概念を理解するために、いくつかの簡単な問題を自分で解決しようとすることができます。
タスクに目を向けます。ある種のボトムアップ分析を使用して算術式を計算します(より正確には、この方法は「オペレーター優先順位の構文分析」と呼ばれます)。 アルゴリズムは最適ではありませんが、理解するのは簡単です。 また、最適ではないが理解しやすいため、よく知られているバブルソートアルゴリズムに似ています。
特に深くならないように、怠zyなナマケモノとして行動し、演算子*(乗算)、+(加算)、および括弧のみをサポートします。 さらに先に進む前に、括弧で停止します。
実際、ブラケットをサポートする必要がないと想像してください。 その場合、式計算アルゴリズムは非常に単純で簡単です。
- 行を左から右にスキャンし、すべての乗算演算子を実行します(たとえば、入力は行1 + 5 * 7 + 3、出力は1 + 35 + 3でした)
- ステップ1で発生したことをスキャンし、すべての加算演算子を実行します(入力1 + 35 + 3で、出力39で判明しました)。
- 結果としてステップ2で何が起こったのかを示します。
解析は必要ありません! 入力構造はフラットであり、解析する必要はありません。 ブラケット(および他の類似物-演算子ブラケットbegin..end、ネストされたブロックなど)をサポートする必要がある場合に必要になります。 入力構造はフラットでなくなり、ツリー状(自己相似、再帰的)になります。今後は、再帰的メソッドと解析メソッドを使用して操作する必要があります。 つまり、たとえば、5 *(2 + 3)は式ですが、(2 + 3)も式です。 これらは両方とも式パーサーに入力できます。 しかし、今は再帰降下法を使用した解析については話していないので、先に進みましょう。
字句解析を処理しないようにするために、String.split関数が字句アナライザになることに同意します(忘れているか、「トピックにまだ」入っていない人のために、字句アナライザは文字列を入力に与えるものです。それを部分文字列(トークン)の配列にカットします。この場合、たとえば '(2 + 3)'-> ['('、 '2'、 '+'、 '3'、 ')'])
アルゴリズムの非公式の説明は次のとおりです。
- 行をスキャンして、できる限りすべてのブラケットを開きます。
- 行をスキャンし、可能な限りすべての乗算演算子を実行します。
- 行をスキャンし、可能な限りすべての加算演算子を実行します。
乗算または加算演算子を実行できることをどのように理解しますか? 演算子の左と右の両方が数字であることを示す記号。 括弧を展開できることをどのように理解しますか? 括弧内にあるのは、他の括弧がない式のみです。
実際、プログラムの本文とその成果の結論から、それがさらに明らかになると思われます。 (プログラムにエラーがあるかもしれないことに注意してください;それは単にデモ目的のために書かれました)。
package demoexprevaluator; import java.io.PrintStream; import java.util.ArrayList; public class DemoExprEvaluator {
仕事の結論:
They want us to calculate:2+300*(4+2)*((8+5))
2+300*(4+2)*((8+5))
about to eval ewp:4+2
2+300*6*((8+5))
about to eval ewp:8+5
2+300*6*(13)
about to eval ewp:13
2+300*6*13
The result is: 23402こっち 実際のLRアナライザーははるかに複雑で、通常は手動で作成されませんが、LRアナライザーの文法コードを生成するbison(以前のyacc)などの正式な文法と特別なツールを使用して自動的に生成されます。 しかし、このようなアナライザーの説明で使用されているshift-reduceの用語がより明確になったことを望んでいます。 行をスキャンし、トークンをスタックに追加したときに、シフトを行いました。 乗算、加算、または拡張されたブラケットの演算子を適用したとき-削減しました。
最後に、LL分析(再帰降下)について説明します。 歴史的には、LRよりも早く登場しましたが、多かれ少なかれ一般的な意見は、LLアナライザーは比較的手で書くのが比較的簡単であり、LRは通常ジェネレーターを使用して作成されるというものです。 しかし、LLアナライザーの自動生成用のツールもあります。最も有名なものの1つはANTLRです。 おそらく、LLアナライザーを手動で作成できるため、このようなツールでの作業が簡単になります。 どちらのアプローチ(LLまたはLR)を使用するかは空虚な質問なので、答えはおそらく「誰が何を好きで、誰が最高のスキルを持っているか」です。
それにもかかわらず、LL分析は別の記事に値します。これについては将来書くかもしれません(JSONのようなものを分析します)。