お父さん、Plekhanov Stanislav Petrovichを記念して献身的です。
論理回路を合成し、最小限の要素数で結果を取得する必要がある場合、ほとんどの場合、カルノーカードが使用されます。 カルノーマップは、高等教育機関、工学コースなどで研究されています。 ただし、論理関数に5〜6個の入力がある場合、Carnotカードの使用は非常に問題が多く、入力変数の数が多いと完全に不可能になります。 驚くべきことに、Carnotカードよりもはるかに単純で効率的な方法がありますが、ほとんどの開発者はそれを認識していません。
ブール関数を最小化する方法は、他の既存の方法よりもはるかに効果的であり、いわゆる「対称カード」の使用に基づいています[1,2]。 カードが対称と呼ばれる理由は、次の話から明らかになります。 この方法を例で説明します。
図5に示すように、真理値表に5つの入力変数を与えます。 1。

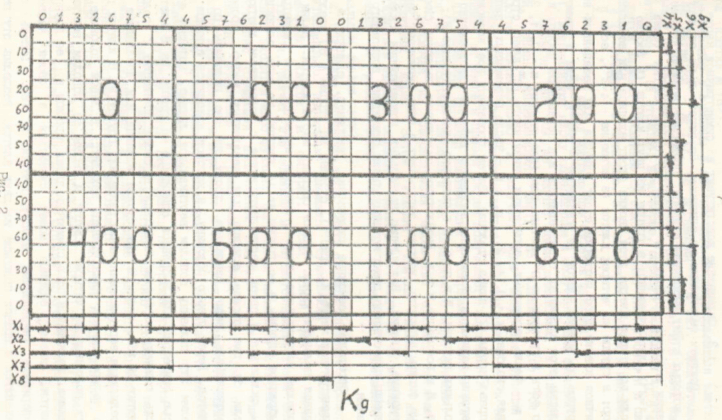
関数Fの値「-」は「無関心」状態を意味し、このような入力変数のセットは発生せず、関数の値は最小化の過程でゼロまたは1に任意に割り当てることができることを思い出してください。 最初に行うことは、8進法で入力セットに番号を付けることです(図1の最後の列)。 その後、最も対称的なカードがいっぱいになります。 5つの変数の対称マップを図2に示します。
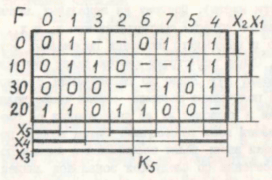
描画方法は後で示しますが、シーケンス0、1、3、2、6、7、5、4と行のシーケンス(8進法では「10」)-0、10を形成する列インデックスに注意を払いたいと思います。 、30、20。
そのようなテーブルに記入することは、カルノーカードよりもはるかに簡単です。 これを行うには、真理値表から8つの値を取得し、対応する行に入力します(列インデックスは、入力セットの8つの値に対応します)。 その後、彼らは実際にブール関数を最小化し始めます。 ここでは、このマップに名前を付ける対称プロパティが使用されます。
単位でマップを最小化します。 行0とインデックスが「1」の列に1つずつ考えてみましょう。 このユニットに対して「対称」なすべてのセルをチェックします。 最初は「ペア」、つまり、列「0」と「1」の間を通る垂直軸に対して相対的です。 行0およびインデックス0のセルになります。値は「0」であるため、これら2つの値を「接着」することはできません。 「4」の対称性を確認します。つまり、垂直軸に対して、列1と3の間を通過します。これは行0とインデックス3のセルです。「-」の値があるため、「1」にすると、(接着剤」)それを私たちのユニットに。 次に、列2と列6の間の対称軸に対応する行0のセル5を確認します(ユニットに接着することもできます)。 「16」の次の対称性は、行0と10の間の水平軸に対する行10と列1のセルです。そして、「32」の対称性は、行20と列1のセルです。行10および30。
私たちの仕事は、私たちのユニティを、それと対称的な他の人たちと接着することにより、最大の可能な数字を見つけることです。 セル(行-列)をカバーするそのような図は、0-1、0-3、0-7、0-5、10-1、10-3、10-7、10-5のみです。 このセットに対応するimplicantを取得するには、このグループを直接または逆の形式で記述する変数を見つける必要があります。 変数X1を取得します(図2では、右の垂直線で示されています。0と10の行は逆の値に対応する太い線で、30と20の行は直接値に対応する細い線です)。 1のグループ全体が行0と10に分類されるため、X1は暗黙の形式で逆形式になります。 右側にも示されている変数X2は、グループがこの変数の逆の値(行0)と直接の値(行10)の両方に該当するため、暗黙の値を入力しません。 同様に、対称マップの下部にある水平線で示される変数X3およびX4は、暗黙の対象にはならず、ユニットのグループ全体が変数X5の直接値によって記述されるため、変数X5が入力されます。 最後に、ユニットのグループは(X1ではなく)* X5として表されます。
行0および列1のユニットを処理した後、すでに形成されたグループに含まれていない残りのユニットを探します。 行0とインデックス4(最後の列)に1つを取ります。 これから、2つの等しく大きなグループを取得できます。最初のグループには行0と10のセル、列5と4のインデックス、2番目のグループ-最後の列のすべてのセルが含まれます。 グループは、インプラント(X1ではない)* X3 *(X4ではない)およびX3 *(X4ではない)*(X5ではない)に対応します。 複数のカバレッジの可能性がある場合、最小ブール関数の複数のバリアントも存在する可能性があることに注意してください。 すべてのユニットが少なくとも1つのグループでカバーされるまで、同様の方法で行動します。
最後に、2つのオプションの形式で、最小の選言的に正規の形式があります。

次の図に示すように、変数の数が異なる対称マップの外観は似ています。
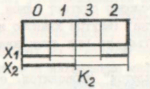


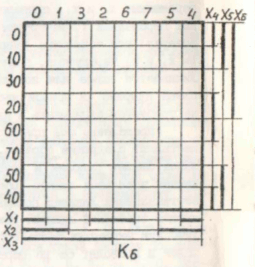
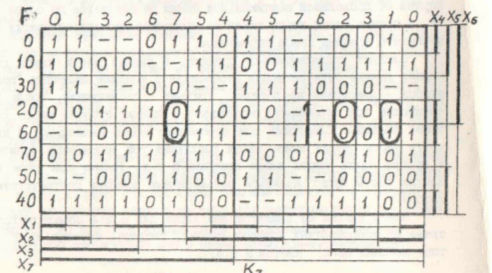
対称カードを使用すると、次のことができることに注意してください。
1.真理値表への記入を大幅に高速化し、簡素化します。
2.最小化された関数の引数の数を数倍増やす。
3.対称性により、最小化プロセスを大幅に簡素化します。
1. Medvedev S.S. ブール関数を最小化するための8進数カード。 オートマトンの理論。 土 記事、サイバネティックス研究所、ソ連科学アカデミー、1966年、p。 45-49。
2. Plekhanov S.P. 対称カードは、大規模デジタルデバイスの設計でブール関数を最小化する強力な手段です。 -電子工学、Ser。 10、マイクロ電子デバイス。 -1991。問題。 4(88)、p。 27-29。