セグメント[0,1]のすべての実数に番号を付けます

集合論に関するすべての教科書の実数の不可算性の証拠として、いわゆるカントール対角法が与えられています （詳細については、「数学とは何か」、Authors Courant、Robbins、§4.無限の数学的分析を参照してください。不可算
連続体。）。 この方法は、範囲[0,1]に属する実数のサブセットの不可算性を証明します。 ただし、証拠をよく見ると、シリアル番号が10進数で増加するたびに可能なオプションの指数関数的な増加を考慮していないことが明らかになります。

Cantorは次のように主張します（ただし、無限小数部に関してのみ）。小数部をリストの形式で任意に配置し、それらに番号を付けて対角線を考慮します。 対角線上の各桁に1を追加すると、このリストにない数値が得られます。 それは、直感的なレベルでの疑問と同じ点です。

対角法の欠如

私たちが話していることを理解するために、次の例を使用して対角法の考えを考えてみましょう。 次の図に示すように、0、a ₁ a ₂ a ₃ a ₄ a ₅の形式の最終的な部分をリストから作成して、5 * 5の正方形を取得します。



Cantor法を適用しますが、実際、この正方形には0.22226という数字はありません。 しかし、それは長方形5 * n ⁵にあります。ここで、5は小数点以下の桁数で、nは使用される計算の桁数です（この例では、n = 10）。 これは、長さが小数点以下5桁であるすべての可能な分数の組み合わせの数がn ^{5であるため}です。

正方形のサイズを無限に押し上げると、いわゆるカントール対角法が得られます。 しかし、それは正方形ではなく、サイズm * n ^mの長方形です。ここで、mは小数点以下の位置の数で、m->∞は無限に必要です。

私のアプローチのアイデア

範囲[0、1]に属するすべての実数に番号を付けるには、指数関数的に成長するツリーの形式で配置する必要があります。 バイナリシステムで書かれた小数を考えてください。 kを小数点以下の桁数、nを番号体系のアルファベットのサイズとします。 その場合、k = 1から∞までの可能な分数の数はkの関数になります。これは次の図で見ることができます。



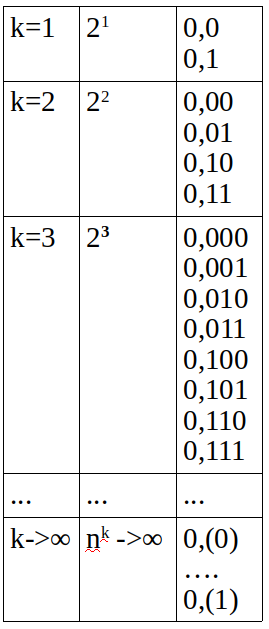レベルの上の表の各行を呼び出します 。 したがって、kは同時にレベル番号と小数点以下の桁数です。

2つのシリアル番号を紹介します。

• 範囲[0,1]からのすべての数値の連続番号付けに使用される汎用カウンター（ C 、カウンター）。
• 各レベルの番号に個別に番号を付けるために使用されるレベルカウンター（ L 、レベルカウンターごと）は、次のレベルに移動するときにゼロにリセットされます。 最初のレベルでは、Lは値1と2を取り、2番目は1、2、3、4などを取ります。

以下の表のように、すべての2進10進小数を2進ツリーとして表示します。



小数点位置の個々の数字は、個別のセルに配置されます。 このような各数字の反対側で、次のように2つのインデックスCとLを記述します。NCL。Nは数字の値です。

CとLはkの関数であり、数値N自体の桁であることが明らかになります。C= fC（k; N）、L = fL（k; N）。 また、範囲[0,1]からすべての番号に番号を付けることができることも明らかになります。 各レベルを順番に調べ、特定のレベルで可能なすべての組み合わせに順番に番号を付けます。

カウンターC = f ^C （N）およびL = f ^L （k; N）の分析依存性を導き出すことは残っています。

便宜上、L（k; N）をL _kとして示します。
L _0-1 = 0と仮定します。

テーブルを注意深く調べると、次のパターンが現れます。
L _k =（L _k-1-1 ）* S + N + 1
ここで、k> = 1、Nは小数部の現在の桁、S = | {0,1} | = 2-アルファベットバイナリシステムのサイズ。 記録| A | は集合Aのべき乗を意味します。有限集合の場合、それはその中の要素の数です。

明らかに、Cには、以前のすべてのレベルのすべての組み合わせの合計と、現在のレベルのL番号が含まれています。 C（N）= _{Σi∈[1、k-1]} 2 ⁱ + L（k; N）。

例

任意の数値0、0101を考えます。 シリアル番号はC（0.0101）= 2 ¹ + 2 ² + 2 ³ + L ₄ = 2 + 4 + 8 + 6 = 20です。

計算：

L ₁ =（L ₀ -1）* 2 + 0 + 1 = 0 * 2 + 0 + 1 = 1
L ₂ =（L 1-1）* 2 + 1 + 1 =（1-1）* 2 + 1 + 1 = 2
L ₃ =（L _2-1 ）* 2 + 0 + 1 =（2-1）* 2 + 0 + 1 = 3
L ₄ =（L _3-1 ）* 2 + 1 + 1 =（3-1）* 2 + 1 + 1 = 6

可視化：



任意の数値0、1001を考えます。 シリアル番号はC（0,1001）= 2 ¹ + 2 ² + 2 ³ + L ₄ = 2 + 4 + 8 + 10 = 24です。
L ₁ =（L _0-1 ）* 2 + 1 + 1 = 0 * 2 + 1 + 1 = 2
L ₂ =（L 1-1）* 2 + 0 + 1 =（1-1）* 2 + 0 + 1 = 3
L ₃ =（L _2-1 ）* 2 + 0 + 1 =（2-1）* 2 + 0 + 1 = 5
L ₄ =（L _3-1 ）* 2 + 1 + 1 =（3-1）* 2 + 1 + 1 = 10

可視化：

結論

したがって、範囲[0,1]からすべての実数を完全に連続的に番号付けするアルゴリズムを取得しました;さらに、任意の長さの任意の小数部分を取得する場合、その一意の序数を計算できます。

PS私が提案したアルゴリズムにエラーがある場合、それは私の不注意のために表示されません-コメントでそれについて書くための大きな要求。

PPSエラーがなければ、| [0,1] | = | N |！ つまり 範囲[0,1]のすべての実数に番号を付けることができます！