ニューラルネットワークを使用して関数を近似します

ニューラルネットワークを操作するためのライブラリを開発するために、トレーニングと予測のためのニューラルネットワークアルゴリズムを使用して、単一の引数の関数を近似する問題を解決します。

エントリー

関数fを与えます：[x0、x1]-> R

与えられた関数fを式で近似します

P(x) = SUM W[i]*E(x,M[i]) 

どこで

• i = 1..n
• RのM [i]
• RのW [i]
• E（x、M）= {0、for x <M; 1/2、x = M; 1、x> Mの場合

明らかに、間隔（x0、x1）上のM [i]の値の均一な分布では、式P（x）が関数f（x）を最もよく近似するような量W [i]があります。 さらに、間隔（x0、x1）で定義され、昇順で順序付けられたM [i]の値について、式P（x）の量W [i]を計算するための逐次アルゴリズムを記述することができます。

そして、これがニューラルネットワークです

式P（x）= SUM W [i] * E（x、M [i]）を、1つの入力ニューロン、1つの出力ニューロン、およびn個の隠れ層ニューロンを含むニューラルネットワークモデルに変換します。

 P(x) = SUM W[i]*S(K[i]*x + B[i]) + C 

どこで

• 変数x-1つのニューロンで構成される「入力」層
• {K、B}-n個のニューロンと活性化関数で構成される「隠れた」層のパラメーター-シグモイド
• {W、C}-「出力」層のパラメーター。1つのニューロンで構成され、入力の加重和を計算します。
• Sはシグモイド、

ながら

• 「非表示」レイヤーの初期パラメーターK [i] = 1
• 「非表示」レイヤーB [i]の初期パラメーターは、セグメントに均等に分散されます（-x1、-x0）

ニューラルネットワークK、B、W、およびCのすべてのパラメーターは、関数fの値のサンプル（x、y）でニューラルネットワークをトレーニングすることによって決定されます。

シグモイド

シグモイドは滑らかな単調増加非線形関数です

• S（x）= 1 /（1 + exp（-x））。

プログラム

Tensorflowパッケージを使用して、ニューラルネットワークを記述します。

 #        x = tf.placeholder(tf.float32, [None, 1], name="x") #        y = tf.placeholder(tf.float32, [None, 1], name="y") #   nn = tf.layers.dense(x, hiddenSize, activation=tf.nn.sigmoid, kernel_initializer=tf.initializers.ones(), bias_initializer=tf.initializers.random_uniform(minval=-x1, maxval=-x0), name="hidden") #   model = tf.layers.dense(nn, 1, activation=None, name="output") #    cost = tf.losses.mean_squared_error(y, model) train = tf.train.GradientDescentOptimizer(learn_rate).minimize(cost) 

トレーニング

 init = tf.initializers.global_variables() with tf.Session() as session: session.run(init) for _ in range(iterations): train_dataset, train_values = generate_test_values() session.run(train, feed_dict={ x: train_dataset, y: train_values }) 

全文

 import math import numpy as np import tensorflow as tf import matplotlib.pyplot as plt x0, x1 = 10, 20 #    test_data_size = 2000 #      iterations = 20000 #    learn_rate = 0.01 #   hiddenSize = 10 #    #     def generate_test_values(): train_x = [] train_y = [] for _ in range(test_data_size): x = x0+(x1-x0)*np.random.rand() y = math.sin(x) #   train_x.append([x]) train_y.append([y]) return np.array(train_x), np.array(train_y) #        x = tf.placeholder(tf.float32, [None, 1], name="x") #        y = tf.placeholder(tf.float32, [None, 1], name="y") #   nn = tf.layers.dense(x, hiddenSize, activation=tf.nn.sigmoid, kernel_initializer=tf.initializers.ones(), bias_initializer=tf.initializers.random_uniform(minval=-x1, maxval=-x0), name="hidden") #   model = tf.layers.dense(nn, 1, activation=None, name="output") #    cost = tf.losses.mean_squared_error(y, model) train = tf.train.GradientDescentOptimizer(learn_rate).minimize(cost) init = tf.initializers.global_variables() with tf.Session() as session: session.run(init) for _ in range(iterations): train_dataset, train_values = generate_test_values() session.run(train, feed_dict={ x: train_dataset, y: train_values }) if(_ % 1000 == 999): print("cost = {}".format(session.run(cost, feed_dict={ x: train_dataset, y: train_values }))) train_dataset, train_values = generate_test_values() train_values1 = session.run(model, feed_dict={ x: train_dataset, }) plt.plot(train_dataset, train_values, "bo", train_dataset, train_values1, "ro") plt.show() with tf.variable_scope("hidden", reuse=True): w = tf.get_variable("kernel") b = tf.get_variable("bias") print("hidden:") print("kernel=", w.eval()) print("bias = ", b.eval()) with tf.variable_scope("output", reuse=True): w = tf.get_variable("kernel") b = tf.get_variable("bias") print("output:") print("kernel=", w.eval()) print("bias = ", b.eval()) 

それが起こったことです

• 青は元の関数です。
• 赤色-関数の近似

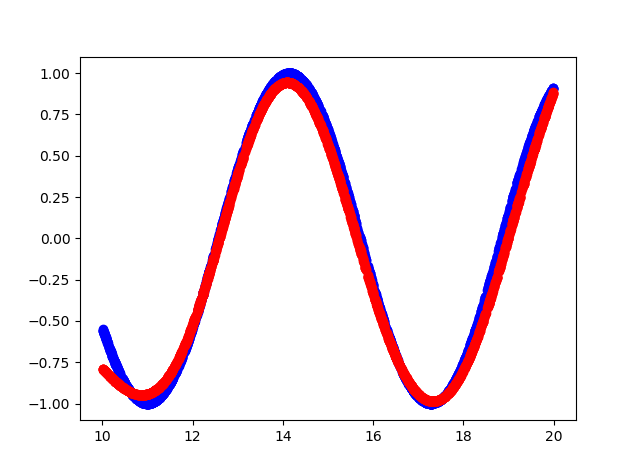
コンソール出力

 cost = 0.15786637365818024 cost = 0.10963975638151169 cost = 0.08536215126514435 cost = 0.06145831197500229 cost = 0.04406769573688507 cost = 0.03488277271389961 cost = 0.026663536205887794 cost = 0.021445846185088158 cost = 0.016708852723240852 cost = 0.012960446067154408 cost = 0.010525770485401154 cost = 0.008495906367897987 cost = 0.0067353141494095325 cost = 0.0057082874700427055 cost = 0.004624188877642155 cost = 0.004093789495527744 cost = 0.0038146725855767727 cost = 0.018593043088912964 cost = 0.010414039716124535 cost = 0.004842184949666262 hidden: kernel= [[1.1523403 1.181032 1.1671464 0.9644377 0.8377886 1.0919508 0.87283015 1.0875995 0.9677301 0.6194152 ]] bias = [-14.812331 -12.219926 -12.067375 -14.872566 -10.633507 -14.014006 -13.379829 -20.508204 -14.923473 -19.354435] output: kernel= [[ 2.0069902 ] [-1.0321712 ] [-0.8878887 ] [-2.0531905 ] [ 1.4293027 ] [ 2.1250408 ] [-1.578137 ] [ 4.141281 ] [-2.1264815 ] [-0.60681605]] bias = [-0.2812019] 

ソースコード

https://github.com/dprotopopov/nnfunc