Anacondaによるハンズオンデータサイエンスの書籍の章の翻訳を紹介します
「予測データ分析-モデリングと検証」



さまざまなデータ分析を実施する主な目的は、パターンを検索して、今後何が起こるかを予測することです。 株式市場では、研究者や専門家がさまざまなテストを実施して、市場メカニズムを理解しています。 この場合、多くの質問をすることができます。 今後5年間の市場指数のレベルはどうなりますか？ 次のIBM価格帯はどうなりますか？ 市場のボラティリティは将来的に増減しますか？ 政府が税政策を変更した場合、どのような影響がありますか？ ある国が他の国と貿易戦争を開始した場合の潜在的な利益と損失は何ですか？ いくつかの関連変数を分析して、消費者の行動をどのように予測しますか？ 大学院生が卒業する可能性を予測できますか？ ある特定の病気の特定の行動の間の関係を見つけることができますか？

したがって、次のトピックを検討します。

• 予測データ分析について
• 便利なデータセット
• 将来のイベントの予測
• モデル選択
• グレンジャー因果関係テスト

予測データ分析について

人々は将来のイベントに関して多くの質問をするかもしれません。

• 投資家は、株価の将来の動きを予測できれば、大きな利益を上げることができます。
• 企業は、製品の傾向を予測できれば、株価と市場シェアを高めることができます。
• 政府は、高齢化が社会や経済に与える影響を予測できれば、州予算やその他の関連する戦略的決定に関してより良い政策を策定するインセンティブが増えるでしょう。
• 大学は、卒業生に設定された品質とスキルの面で市場の需要を十分に理解できれば、将来の労働力のニーズを満たすために、より良いプログラムのセットを開発したり、新しいプログラムを立ち上げたりできます。

より良い予後のために、研究者は多くの質問を考慮すべきです。 たとえば、サンプルデータが小さすぎませんか？ 不足している変数を削除する方法は？ このデータセットは、データ収集手順に関して偏っていますか？ 極値や排出量についてどう思いますか？ 季節性とは何ですか、どのように対処しますか？ どのモデルを使用する必要がありますか？ この章では、これらの問題のいくつかについて説明します。 便利なデータセットから始めましょう。

便利なデータセット

最適なデータソースの1つはUCI Machine Learning Repositoryです。 サイトにアクセスすると、次のリストが表示されます。



たとえば、最初のデータセット（Abalone）を選択すると、次のように表示されます。 スペースを節約するために、上部のみが表示されます。



ここから、ユーザーはデータセットをダウンロードして変数定義を見つけることができます。 次のコードを使用して、データセットをロードできます。

dataSet<-"UCIdatasets" path<-"http://canisius.edu/~yany/RData/" con<-paste(path,dataSet,".RData",sep='') load(url(con)) dim(.UCIdatasets) head(.UCIdatasets) 

対応する出力は次のとおりです。



前の結論から、データセットには427の観測値（データセット）があることがわかります。 それぞれについて、 Name、Data_Types、Default_Task、Attribute_Types、N_Instances （インスタンスの数）、 N_Attributes （属性の数）、 Yearなどの7つの関連する関数があります。 Default_Taskという変数は、各データセットの主な用途として解釈できます。 たとえば、 Abaloneと呼ばれる最初のデータセットをClassificationに使用できます。 一意の（）関数を使用して、次に示すすべての可能なDefault_Taskを検索できます。

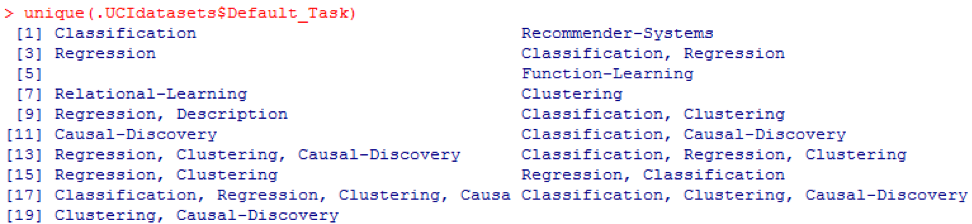
RパッケージAppliedPredictiveModeling

このパッケージには、この章や他の章で使用できる多くの便利なデータセットが含まれています。 これらのデータセットを見つける最も簡単な方法は、次に示すhelp（）関数を使用することです。

 library(AppliedPredictiveModeling) help(package=AppliedPredictiveModeling) 

ここでは、これらのデータセットをロードする例をいくつか示します。 1つのデータセットを読み込むには、 data（）関数を使用します 。 abaloneという最初のデータセットには、次のコードがあります。

 library(AppliedPredictiveModeling) data(abalone) dim(abalone) head(abalone) 

出力は次のとおりです。



場合によっては、大きなデータセットにはいくつかのサブデータセットが含まれます。

 library(AppliedPredictiveModeling) data(solubility) ls(pattern="sol") 

 [1] "solTestX" "solTestXtrans" "solTestY" [4] "solTrainX" "solTrainXtrans" "solTrainY" 

各データセットをロードするには、関数dim（） 、 head（） 、 tail（）およびsummary（）を使用できます。

時系列分析

時系列は、多くの場合、それらの間隔が等間隔である連続した瞬間に取得された値のセットとして定義できます。 年次、四半期、月次、週次、日次など、さまざまな期間があります。 GDP（国内総生産）の時系列では、通常、四半期または年次を使用します。 見積もり-年次、月次、および日次の頻度。 次のコードを使用して、米国のGDPに関するデータを四半期ごとと年間の両方で取得できます。

 ath<-"http://canisius.edu/~yany/RData/" dataSet<-"usGDPannual" con<-paste(path,dataSet,".RData",sep='') load(url(con)) head(.usGDPannual) 

 YEAR GDP 1 1930 92.2 2 1931 77.4 3 1932 59.5 4 1933 57.2 5 1934 66.8 6 1935 74.3 

 dataSet<-"usGDPquarterly" con<-paste(path,dataSet,".RData",sep='') load(url(con)) head(.usGDPquarterly) 

  DATE GDP_CURRENT GDP2009DOLLAR 1 1947Q1 243.1 1934.5 2 1947Q2 246.3 1932.3 3 1947Q3 250.1 1930.3 4 1947Q4 260.3 1960.7 5 1948Q1 266.2 1989.5 6 1948Q2 272.9 2021.9 

ただし、時系列分析には多くの質問があります。 たとえば、マクロ経済学の観点から、ビジネスまたは経済のサイクルがあります。 産業や企業には季節性があります。 たとえば、農業産業を使用すると、農家は春と秋の季節により多くを費やし、冬に少なく費やします。 小売業者にとっては、年末には莫大な資金が流入します。

時系列を操作するには、Rパッケージに含まれるtimeSeriesと呼ばれる多くの便利な機能を使用できます。 この例では、毎週の頻度で毎日の平均データを取得します。

 library(timeSeries) data(MSFT) x <- MSFT by <- timeSequence(from = start(x), to = end(x), by = "week") y<-aggregate(x,by,mean) 

また、 head（）関数を使用していくつかの観察結果を確認することもできます。

 head(x) 

 GMT Open High Low Close Volume 2000-09-27 63.4375 63.5625 59.8125 60.6250 53077800 2000-09-28 60.8125 61.8750 60.6250 61.3125 26180200 2000-09-29 61.0000 61.3125 58.6250 60.3125 37026800 2000-10-02 60.5000 60.8125 58.2500 59.1250 29281200 2000-10-03 59.5625 59.8125 56.5000 56.5625 42687000 2000-10-04 56.3750 56.5625 54.5000 55.4375 68226700 

 head(y) 

 GMT Open High Low Close Volume 2000-09-27 63.4375 63.5625 59.8125 60.6250 53077800 2000-10-04 59.6500 60.0750 57.7000 58.5500 40680380 2000-10-11 54.9750 56.4500 54.1625 55.0875 36448900 2000-10-18 53.0375 54.2500 50.8375 52.1375 50631280 2000-10-25 61.7875 64.1875 60.0875 62.3875 86457340 2000-11-01 66.1375 68.7875 65.8500 67.9375 53496000 

将来のイベントの予測

移動平均、回帰、自己回帰など、未来を予測するときに使用できる多くの方法があります。まず、最も単純な移動平均から始めましょう。

 movingAverageFunction<- function(data,n=10){ out= data for(i in n:length(data)){ out[i] = mean(data[(i-n+1):i]) } return(out) } 

前のコードでは、期間数のデフォルト値は10 です。timeSeriesというRパッケージに含まれるMSFTというデータセットを使用できます（次のコードを参照）。

 library(timeSeries) data(MSFT) p<-MSFT$Close # ma<-movingAverageFunction(p,3) head(p) 

 [1] 60.6250 61.3125 60.3125 59.1250 56.5625 55.4375 

 head(ma) 

 [1] 60.62500 61.31250 60.75000 60.25000 58.66667 57.04167 

 mean(p[1:3]) 

 [1] 60.75 

 mean(p[2:4]) 

 [1] 60.25 

手動モードでは、 xの最初の3つの値の平均がyの 3番目の値と一致することがわかります。 ある意味では、移動平均を使用して将来を予測できます。

次の例では、来年の予想市場リターンを評価する方法を示します。 ここでは、S＆P500インデックスと過去の平均年間値を予想値として使用します。 最初のいくつかのコマンドは、 .sp500monthlyという関連データセットをロードするために使用されます。 このプログラムの目的は、年間平均と90％の信頼区間を評価することです。

 library(data.table) path<-'http://canisius.edu/~yany/RData/' dataSet<-'sp500monthly.RData' link<-paste(path,dataSet,sep='') load(url(link)) #head(.sp500monthly,2) p<-.sp500monthly$ADJ.CLOSE n<-length(p) logRet<-log(p[2:n]/p[1:(n-1)]) years<-format(.sp500monthly$DATE[2:n],"%Y") y<-data.frame(.sp500monthly$DATE[2:n],years,logRet) colnames(y)<-c("DATE","YEAR","LOGRET") y2<- data.table(y) z<-y2[,sum(LOGRET),by=YEAR] z2<-na.omit(z) annualRet<-data.frame(z2$YEAR,exp(z2[,2])-1) n<-nrow(annualRet) std<-sd(annualRet[,2]) stdErr<-std/sqrt(n) ourMean<-mean(annualRet[,2]) min2<-ourMean-2*stdErr max2<-ourMean+2*stdErr cat("[min mean max ]\n") 

 [min mean max ] 

 cat(min2,ourMean,max2,"\n") 

 0.05032956 0.09022369 0.1301178 

結果からわかるように、S＆P500の過去の平均年間収益率は9％です。 しかし、来年のインデックスの収益性が9％になるとは言えません。 5％から13％になる可能性があり、これらは大きな変動です。

季節性

次の例では、自己相関の使用方法を示します。 まず、 astsaというRパッケージをダウンロードします。これは、適用される統計的時系列分析の略です。 次に、四半期ごとの頻度で米国のGDPを読み込みます。

 library(astsa) path<-"http://canisius.edu/~yany/RData/" dataSet<-"usGDPquarterly" con<-paste(path,dataSet,".RData",sep='') load(url(con)) x<-.usGDPquarterly$DATE y<-.usGDPquarterly$GDP_CURRENT plot(x,y) diff4 = diff(y,4) acf2(diff4,24) 

上記のコードでは、 diff（）関数は差を受け入れます。たとえば、現在の値から前の値を引いたものです。 2番目の入力値は遅延を示します。 acf2（）という関数を使用して、ACFおよびPACF時系列を作成および印刷します。 ACFは自己共分散関数を表し、PACFは部分自己相関関数を表します。 関連するグラフは次のとおりです。

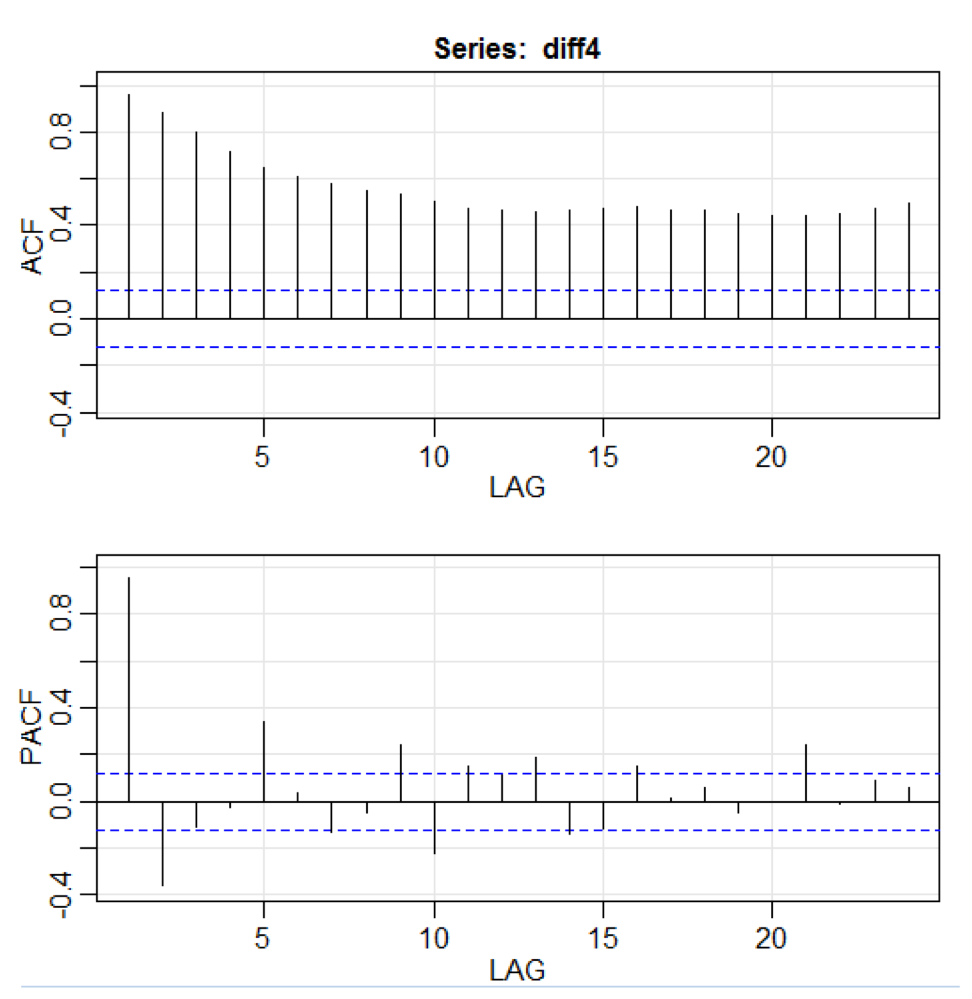
コンポーネントの可視化

グラフを使用できれば、概念とデータセットがはるかに理解しやすいことは明らかです。 最初の例は、過去50年間の米国のGDPの変動を示しています。

 path<-"http://canisius.edu/~yany/RData/" dataSet<-"usGDPannual" con<-paste(path,dataSet,".RData",sep='') load(url(con)) title<-"US GDP" xTitle<-"Year" yTitle<-"US annual GDP" x<-.usGDPannual$YEAR y<-.usGDPannual$GDP plot(x,y,main=title,xlab=xTitle,ylab=yTitle) 

対応するスケジュールは次のとおりです。



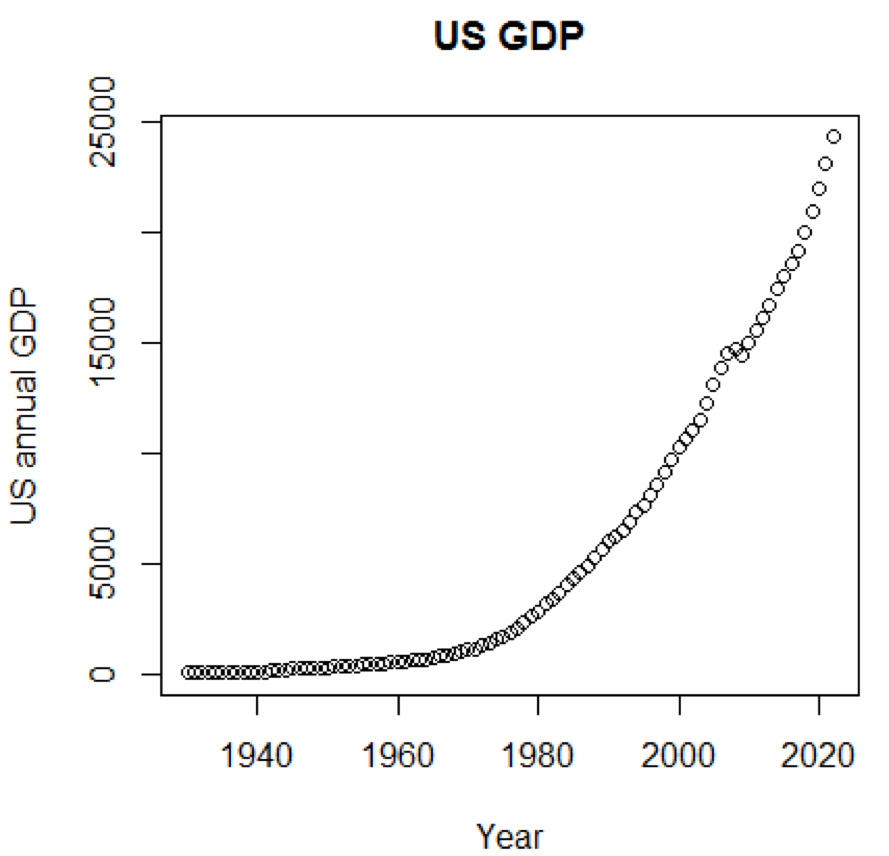
GDPに対数スケールを使用した場合、次のコードとグラフになります。

 yTitle<-"Log US annual GDP" plot(x,log(y),main=title,xlab=xTitle,ylab=yTitle) 

次のグラフは直線に近いものです。

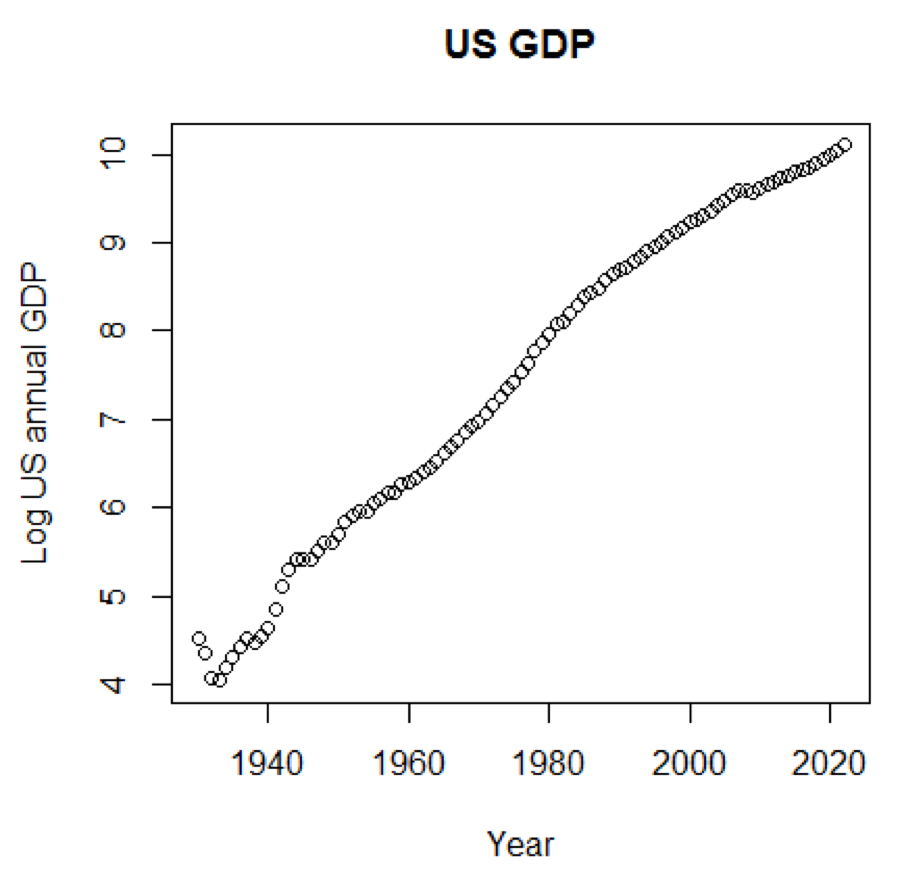
Rパッケージ-LiblineaR

このパッケージは、LIBLINEAR C / C ++ライブラリに基づく線形予測モデルです。 アイリスデータセットの使用例の1つを次に示します。 プログラムは、トレーニングデータを使用して、プラントが属するカテゴリを予測しようとします。

 library(LiblineaR) data(iris) attach(iris) x=iris[,1:4] y=factor(iris[,5]) train=sample(1:dim(iris)[1],100) xTrain=x[train,];xTest=x[-train,] yTrain=y[train]; yTest=y[-train] s=scale(xTrain,center=TRUE,scale=TRUE) # tryTypes=c(0:7) tryCosts=c(1000,1,0.001) bestCost=NA bestAcc=0 bestType=NA # for(ty in tryTypes){ for(co in tryCosts){ acc=LiblineaR(data=s,target=yTrain,type=ty,cost=co,bias=1,cross=5,verbose=FALSE) cat("Results for C=",co,": ",acc," accuracy.\n",sep="") if(acc>bestAcc){ bestCost=co bestAcc=acc bestType=ty } } } cat("Best model type is:",bestType,"\n") cat("Best cost is:",bestCost,"\n") cat("Best accuracy is:",bestAcc,"\n") # Re-train best model with best cost value. m=LiblineaR(data=s,target=yTrain,type=bestType,cost=bestCost,bias=1,verbose=FALSE) # Scale the test data s2=scale(xTest,attr(s,"scaled:center"),attr(s,"scaled:scale")) pr=FALSE; # Make prediction if(bestType==0 || bestType==7) pr=TRUE p=predict(m,s2,proba=pr,decisionValues=TRUE) res=table(p$predictions,yTest) # Display confusion matrix print(res) # Compute Balanced Classification Rate BCR=mean(c(res[1,1]/sum(res[,1]),res[2,2]/sum(res[,2]),res[3,3]/sum(res[,3]))) print(BCR) 

結論は次のとおりです。 BCRはバランスの取れた分類率です。 このベットでは、高いほど良い：

 cat("Best model type is:",bestType,"\n") 

 Best model type is: 4 

 cat("Best cost is:",bestCost,"\n") 

 Best cost is: 1 

 cat("Best accuracy is:",bestAcc,"\n") 

 Best accuracy is: 0.98 

 print(res) yTest setosa versicolor virginica setosa 16 0 0 versicolor 0 17 0 virginica 0 3 14 print(BCR) 

 [1] 0.95 

Rパッケージ-eclust

このパッケージは、高次元データの解釈された予測モデル用の環境に優しいクラスタリングです。 まず、パッケージのシミュレートされたデータを含むsimdataというデータセットを見てみましょう。

 library(eclust) data("simdata") dim(simdata) 

 [1] 100 502 

 simdata[1:5, 1:6] 

  YE Gene1 Gene2 Gene3 Gene4 [1,] -94.131497 0 -0.4821629 0.1298527 0.4228393 0.36643188 [2,] 7.134990 0 -1.5216289 -0.3304428 -0.4384459 1.57602830 [3,] 1.974194 0 0.7590055 -0.3600983 1.9006443 -1.47250061 [4,] -44.855010 0 0.6833635 1.8051352 0.1527713 -0.06442029 [5,] 23.547378 0 0.4587626 -0.3996984 -0.5727255 -1.75716775 

 table(simdata[,"E"]) 

 0 1 50 50 

前の結論は、データ次元が100 x 502であることを示しています。Yは連続応答ベクトルであり、 EはECLUSTメソッドのバイナリ環境変数です。 E = 0は非露出（n = 50）で、 E = 1は露出（n = 50）です。

次のプログラムRは、フィッシャーのz変換を評価します。

 library(eclust) data("simdata") X = simdata[,c(-1,-2)] firstCorr<-cor(X[1:50,]) secondCorr<-cor(X[51:100,]) score<-u_fisherZ(n0=100,cor0=firstCorr,n1=100,cor1=secondCorr) dim(score) 

 [1] 500 500 

 score[1:5,1:5] 

  Gene1 Gene2 Gene3 Gene4 Gene5 Gene1 1.000000 -8.062020 6.260050 -8.133437 -7.825391 Gene2 -8.062020 1.000000 9.162208 -7.431822 -7.814067 Gene3 6.260050 9.162208 1.000000 8.072412 6.529433 Gene4 -8.133437 -7.431822 8.072412 1.000000 -5.099261 Gene5 -7.825391 -7.814067 6.529433 -5.099261 1.000000 

Fisherのz変換を定義します。 n個のペアx iとy iのセットがあると仮定すると、次の式を使用してそれらの相関を推定できます。



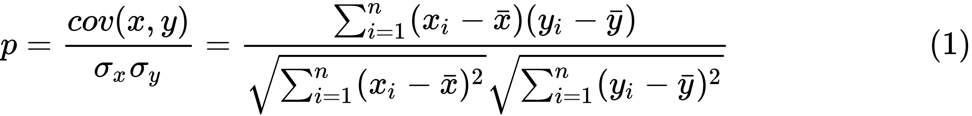
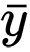
ここで、 pは2つの変数間の相関です。 そして は、ランダム変数xおよびyのサンプル平均です。 zの値は次のように定義されます。



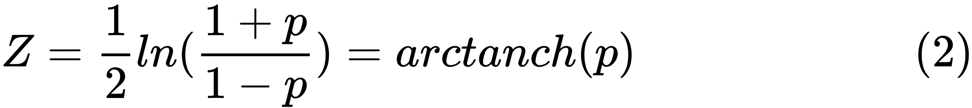lnは自然対数関数、 arctanh（）は逆双曲線正接関数です。

モデル選択

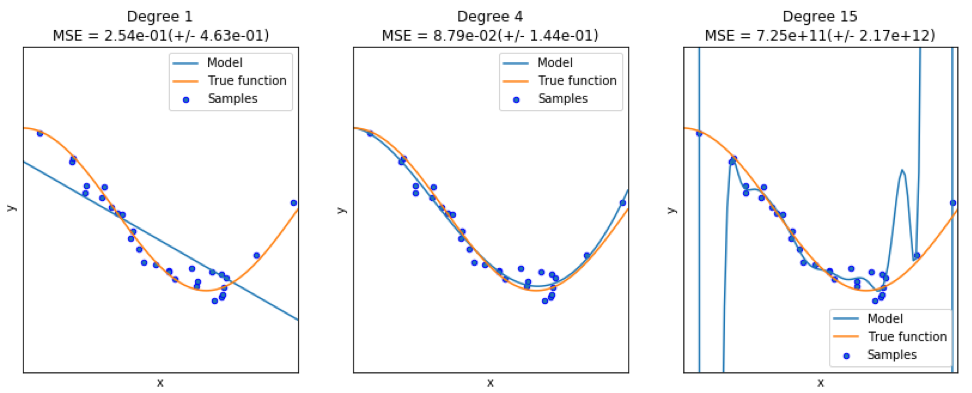
良いモデルを見つけるとき、時々データの不足/過剰に直面します。 次の例はここから引用されています 。 これでの作業の問題と、非線形関数を近似するために多項式機能を使用して線形回帰を使用する方法を示しています。 指定された機能：



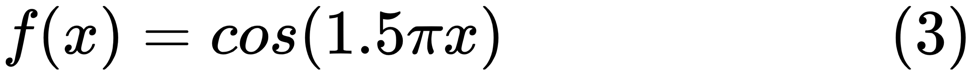
次のプログラムでは、線形モデルと多項式モデルを使用して方程式を近似しようとします。 わずかに変更されたコードをここに示します。 このプログラムは、モデルに対するデータ不足/供給過剰の影響を示しています。

 import sklearn import numpy as np import matplotlib.pyplot as plt from sklearn.pipeline import Pipeline from sklearn.preprocessing import PolynomialFeatures from sklearn.linear_model import LinearRegression from sklearn.model_selection import cross_val_score # np.random.seed(123) n= 30 # number of samples degrees = [1, 4, 15] def true_fun(x): return np.cos(1.5*np.pi*x) x = np.sort(np.random.rand(n)) y = true_fun(x) + np.random.randn(n) * 0.1 plt.figure(figsize=(14, 5)) title="Degree {}\nMSE = {:.2e}(+/- {:.2e})" name1="polynomial_features" name2="linear_regression" name3="neg_mean_squared_error" # for i in range(len(degrees)): ax=plt.subplot(1,len(degrees),i+1) plt.setp(ax, xticks=(), yticks=()) pFeatures=PolynomialFeatures(degree=degrees[i],include_bias=False) linear_regression = LinearRegression() pipeline=Pipeline([(name1,pFeatures),(name2,linear_regression)]) pipeline.fit(x[:,np.newaxis],y) scores=cross_val_score(pipeline,x[:,np.newaxis],y,scoring=name3,cv=10) xTest = np.linspace(0, 1, 100) plt.plot(xTest,pipeline.predict(xTest[:,np.newaxis]),label="Model") plt.plot(xTest,true_fun(xTest),label="True function") plt.scatter(x,y,edgecolor='b',s=20,label="Samples") plt.xlabel("x") plt.ylabel("y") plt.xlim((0,1)) plt.ylim((-2,2)) plt.legend(loc="best") plt.title(title.format(degrees[i],-scores.mean(),scores.std())) plt.show() 

結果のグラフは次のとおりです。

Pythonパッケージ-モデルキャットウォーク

例はここにあります 。

コードの最初の数行は次のとおりです。

 import datetime import pandas from sqlalchemy import create_engine from metta import metta_io as metta from catwalk.storage import FSModelStorageEngine, CSVMatrixStore from catwalk.model_trainers import ModelTrainer from catwalk.predictors import Predictor from catwalk.evaluation import ModelEvaluator from catwalk.utils import save_experiment_and_get_hash help(FSModelStorageEngine) 

対応する結論をここに示します。 スペースを節約するために、上部のみが表示されます。

 Help on class FSModelStorageEngine in module catwalk.storage: class FSModelStorageEngine(ModelStorageEngine) | Method resolution order: | FSModelStorageEngine | ModelStorageEngine | builtins.object | | Methods defined here: | | __init__(self, *args, **kwargs) | Initialize self. See help(type(self)) for accurate signature. | | get_store(self, model_hash) | | ---------------------------------------------------------------------- 

 | Data descriptors inherited from ModelStorageEngine: | | __dict__ | dictionary for instance variables (if defined) | | __weakref__ | list of weak references to the object (if defined) 

Pythonパッケージ-sklearn

sklearnは非常に便利なパッケージであるため、このパッケージの使用例をさらに示す価値があります。 ここに示す例は、パッケージを使用して、bag-of-wordsアプローチを使用してトピックごとにドキュメントを分類する方法を示しています。
この例では、 scipy.sparseマトリックスを使用してオブジェクトを保存し、 スパースマトリックスを効率的に処理できるさまざまな分類器を示します。 この例では、20のニュースグループのデータセットを使用します。 自動的にダウンロードされ、キャッシュされます。 zipファイルには入力ファイルが含まれており、 ここからダウンロードできます 。 コードはこちらから入手できます 。 スペースを節約するために、最初の数行のみが示されています。

 import logging import numpy as np from optparse import OptionParser import sys from time import time import matplotlib.pyplot as plt from sklearn.datasets import fetch_20newsgroups from sklearn.feature_extraction.text import TfidfVectorizer from sklearn.feature_extraction.text import HashingVectorizer from sklearn.feature_selection import SelectFromModel 

対応する出力は次のとおりです。



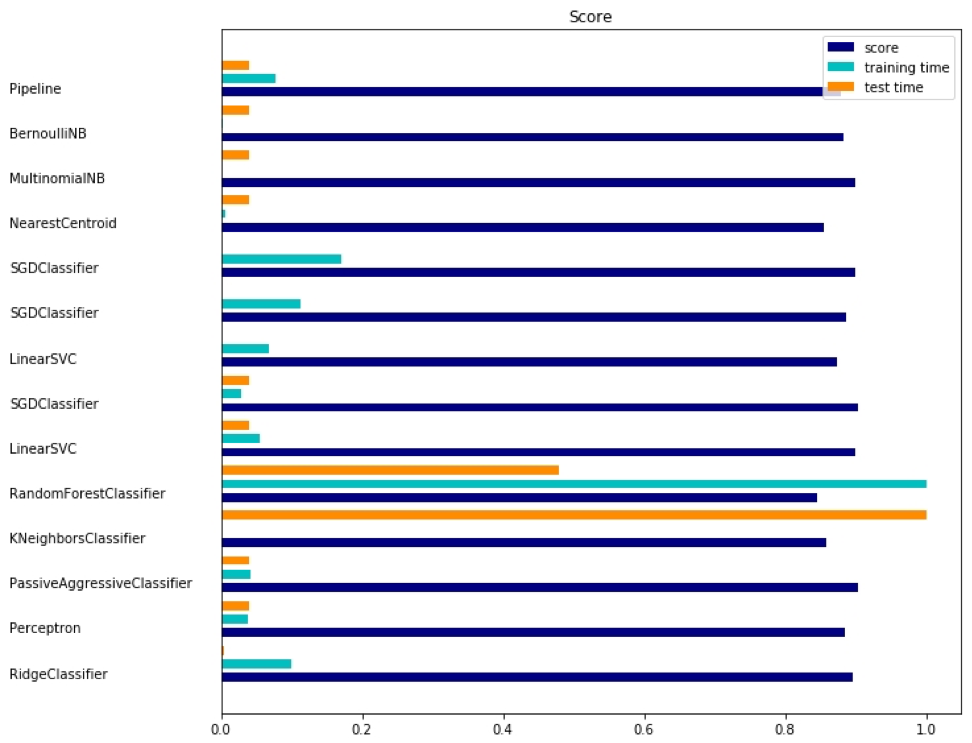
各方法には、評価、トレーニング時間、テスト時間の3つの指標があります。

ジュリアパッケージ-QuantEcon

たとえば、マルコフ連鎖の使用を考えてみましょう。

 using QuantEcon P = [0.4 0.6; 0.2 0.8]; mc = MarkovChain(P) x = simulate(mc, 100000); mean(x .== 1) # mc2 = MarkovChain(P, ["employed", "unemployed"]) simulate(mc2, 4) 

結果：



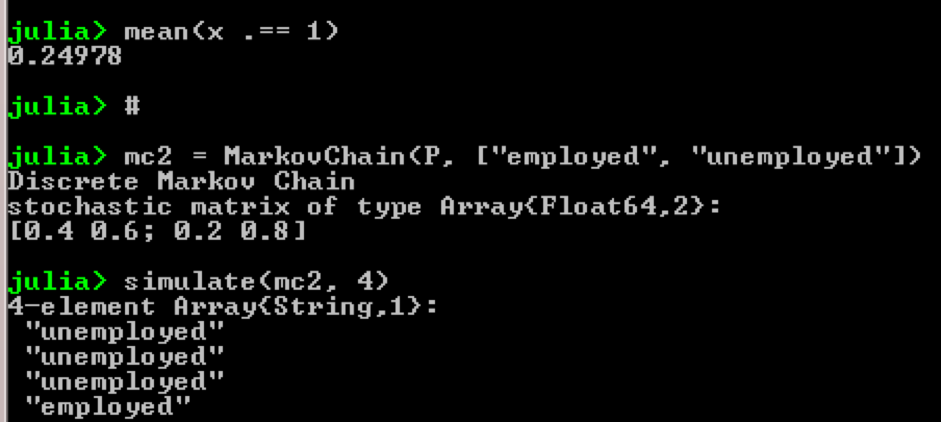
この例の目的は、将来のある経済的地位にある人が別の経済的地位にどのように変化するかを調べることです。 最初に、次のチャートを見てみましょう。



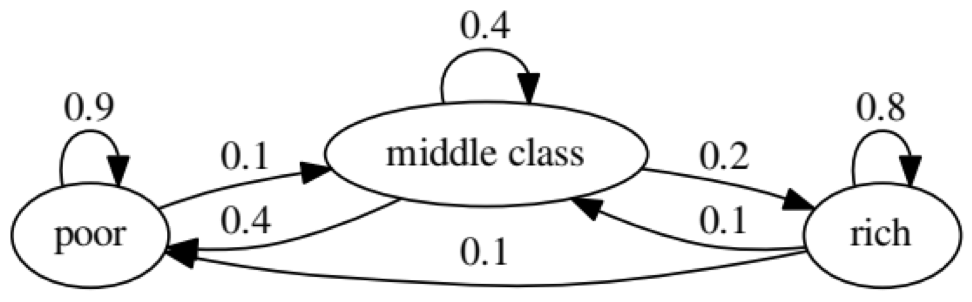
「不良」ステータスの左端の楕円を見てみましょう。 0.9は、このステータスの人が90％の確率で貧困状態になり、10％が中流階級になることを意味します。 次の行列で表すことができます。ゼロはノード間にエッジがない場所です。



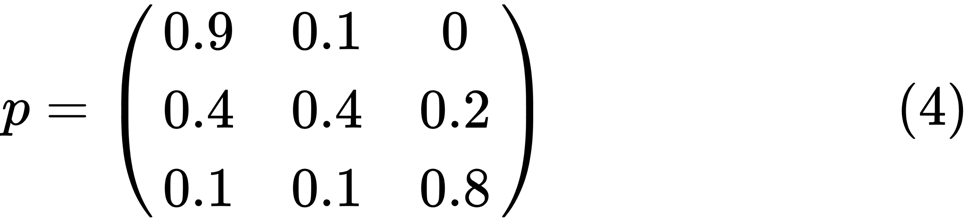
次のような正の整数jとkがある場合、2つの状態xとyは互いに関連していると言われています。



すべての状態が接続されている場合、マルコフ連鎖Pは既約と呼ばれます。 つまり、 xとyがそれぞれ（x、y） について報告される場合です。 次のコードでこれを確認します。

 using QuantEcon P = [0.9 0.1 0.0; 0.4 0.4 0.2; 0.1 0.1 0.8]; mc = MarkovChain(P) is_irreducible(mc) 

次のグラフは極端なケースを表しています。貧しい人の将来の状況は100％貧しいからです。



結果がfalseになるため、次のコードでもこれを確認します 。

 using QuantEcon P2 = [1.0 0.0 0.0; 0.1 0.8 0.1; 0.0 0.2 0.8]; mc2 = MarkovChain(P2) is_irreducible(mc2) 

グレンジャー因果関係テスト

Granger因果関係テストは、1つの時系列が要因であるかどうかを判断し、2番目の時系列を予測するための有用な情報を提供するために使用されます。 次のコードでは、図としてChickEggという名前のデータセットを使用しています。 データセットには、鶏の数と卵の数の2つの列があり、タイムスタンプが付いています。

 library(lmtest) data(ChickEgg) dim(ChickEgg) 

 [1] 54 2 

 ChickEgg[1:5,] 

 chicken egg [1,] 468491 3581 [2,] 449743 3532 [3,] 436815 3327 [4,] 444523 3255 [5,] 433937 3156 

問題は、来年の鶏の数を予測するために今年の卵の数を使用できるかどうかです。

その場合、鶏の数がグレンジャーの卵数の理由になります。 そうでない場合、鶏の数は卵の数のグレンジャーの理由ではないと言います。 関連するコードは次のとおりです。

 library(lmtest) data(ChickEgg) grangertest(chicken~egg, order = 3, data = ChickEgg) 

 Granger causality test Model 1: chicken ~ Lags(chicken, 1:3) + Lags(egg, 1:3) Model 2: chicken ~ Lags(chicken, 1:3) Res.Df Df F Pr(>F) 1 44 2 47 -3 5.405 0.002966 ** --- Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 

モデル1では、雛の数を説明するために、雛の遅れと卵の遅れを使用しようとします。

なぜなら Pの値は非常に小さく（0.01で有意）、卵の数が鶏の数のグレンジャーの理由であると言います。

次のテストは、鶏に関するデータを使用して次の期間を予測できないことを示しています。

 grangertest(egg~chicken, order = 3, data = ChickEgg) 

 Granger causality test Model 1: egg ~ Lags(egg, 1:3) + Lags(chicken, 1:3) Model 2: egg ~ Lags(egg, 1:3) Res.Df Df F Pr(>F) 1 44 2 47 -3 0.5916 0.6238 

次の例では、IBMとS＆P500の収益性をチェックして、それらの原因が別のグレンジャーの理由であることを確認します。

まず、利回り関数を定義します。

 ret_f<-function(x,ticker=""){ n<-nrow(x) p<-x[,6] ret<-p[2:n]/p[1:(n-1)]-1 output<-data.frame(x[2:n,1],ret) name<-paste("RET_",toupper(ticker),sep='') colnames(output)<-c("DATE",name) return(output) } 

 >x<-read.csv("http://canisius.edu/~yany/data/ibmDaily.csv",header=T) ibmRet<-ret_f(x,"ibm") x<-read.csv("http://canisius.edu/~yany/data/^gspcDaily.csv",header=T) mktRet<-ret_f(x,"mkt") final<-merge(ibmRet,mktRet) head(final) 

  DATE RET_IBM RET_MKT 1 1962-01-03 0.008742545 0.0023956877 2 1962-01-04 -0.009965497 -0.0068887673 3 1962-01-05 -0.019694350 -0.0138730891 4 1962-01-08 -0.018750380 -0.0077519519 5 1962-01-09 0.011829467 0.0004340133 6 1962-01-10 0.001798526 -0.0027476933 

これで、入力値で関数を呼び出すことができます。 このプログラムの目標は、IBMの収益性を説明するために市場の遅れを使用できるかどうかをテストすることです。 同様に、市場収益におけるIBMの遅れを説明するためにチェックします。

 library(lmtest) grangertest(RET_IBM ~ RET_MKT, order = 1, data =final) 

 Granger causality test Model 1: RET_IBM ~ Lags(RET_IBM, 1:1) + Lags(RET_MKT, 1:1) Model 2: RET_IBM ~ Lags(RET_IBM, 1:1) Res.Df Df F Pr(>F) 1 14149 2 14150 -1 24.002 9.729e-07 *** --- Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 

結果は、S＆P500が統計的に0.1％と有意であるため、IBMの次期の収益性を説明するために使用できることを示しています。 次のコードは、IBMの遅れがS＆P500の変更を説明しているかどうかを確認します。

 grangertest(RET_MKT ~ RET_IBM, order = 1, data =final) 

 Granger causality test Model 1: RET_MKT ~ Lags(RET_MKT, 1:1) + Lags(RET_IBM, 1:1) Model 2: RET_MKT ~ Lags(RET_MKT, 1:1) Res.Df Df F Pr(>F) 1 14149 2 14150 -1 7.5378 0.006049 ** --- Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 

この結果は、この期間中に、IBMのリターンを使用して、次の期間のS＆P500インデックスを説明できることを示唆しています。