出典 ：ウィキペディアライセンスCC-BY-SA 3.0

公共交通機関で頻繁に旅行する場合、おそらく次のような状況に遭遇しているでしょう。

停止します。 バスは10分ごとに走ると書かれています。 時間に注意してください...最後に、11分後、バスが到着し、考え：なぜ私はいつも不運ですか？

理論的には、バスが10分ごとに到着し、ランダムな時間に到着する場合、平均待機時間は約5分です。 しかし実際には、バスは予定通りに到着しないため、もっと長く待つことができます。 いくつかの合理的な仮定で、驚くべき結論に達することができることがわかります：

平均で10分ごとに到着するバスを待つ場合、平均待ち時間は10分になります。

これは、待機時間のパラドックスと呼ばれることもあります。

以前にアイデアを持っていましたが、これが本当に本当なのかといつも疑問に思っていました。 この記事では、モデリングと確率論の両方の観点からレイテンシのパラドックスを調べ、シアトルの実際のバスデータの一部を見て、（できれば）パラドックスを一度だけ解決します。

パラドックス検査

バスが正確に10分ごとに到着する場合、平均待機時間は5分になります。 バスの間隔にバリエーションを追加すると、平均待ち時間が長くなる理由を簡単に理解できます。

待機時間のパラドックスは、より一般的な現象の特別なケースです。 検査パラドックスについては、アレンダウニーの賢明な記事「The Inspection Paradox Around Us」で詳しく説明しています。

要するに、量を観測する確率が観測される量に関係するときはいつでも、検査の矛盾が生じます。 アレンは、大学生のクラスの平均サイズに関する調査の例を示しています。 学校はグループ内の平均30人の生徒のことを正直に言っていますが、生徒の観点から見ると平均的なグループサイズははるかに大きくなっています。 その理由は、大規模なクラスでは（当然）学生が多いため、調査中に明らかになるからです。

10分間の間隔が宣言されているバススケジュールの場合、到着間隔が10分よりも長い場合があり、短い場合もあります。 ランダムな時間に停止した場合、短い間隔よりも長い間隔に遭遇する可能性が高くなります。 したがって、サンプルではより長い間隔がより一般的であるため、 待機間隔間の平均時間間隔はバス間の平均時間間隔よりも長いことが論理的です。

しかし、レイテンシのパラドックスは、より強力なステートメントを作成します。平均バス間隔が $$$N$分、 乗客の平均待ち時間は $$$2N$分。 これは本当ですか？

レイテンシのシミュレーション

この妥当性を確信するために、まず平均10分で到着するバスの流れをシミュレートします。 正確を期すために、大規模なサンプル：100万バス（または約19年間の24時間の10分間のトラフィック）を取得します。

import numpy as np N = 1000000 # number of buses tau = 10 # average minutes between arrivals rand = np.random.RandomState(42) # universal random seed bus_arrival_times = N * tau * np.sort(rand.rand(N)) 

平均間隔が近いことを確認します $$$\ tau = 10$：

 intervals = np.diff(bus_arrival_times) intervals.mean() 

9.9999879601518398

これで、この期間中に多数の乗客がバス停に到着することをシミュレートし、各乗客が経験する待ち時間を計算できます。 後で使用するために、コードを関数にカプセル化します。

 def simulate_wait_times(arrival_times, rseed=8675309, # Jenny's random seed n_passengers=1000000): rand = np.random.RandomState(rseed) arrival_times = np.asarray(arrival_times) passenger_times = arrival_times.max() * rand.rand(n_passengers) # find the index of the next bus for each simulated passenger i = np.searchsorted(arrival_times, passenger_times, side='right') return arrival_times[i] - passenger_times 

次に、待機時間をシミュレートし、平均を計算します。

 wait_times = simulate_wait_times(bus_arrival_times) wait_times.mean() 

10.001584206227317

パラドックスが予測したように、平均待機時間は10分近くです。

より深く掘り下げる：確率とポアソン過程

そのような状況をシミュレートする方法は？

実際、これは、値を観察する確率が値自体に関連する検査パラドックスの例です。 で示す $$$p（T）$間隔 $$$T$バス停に到着するバスの間。 このようなレコードでは、到着時間の期待値は次のようになります。

$$

$$E [T] = \ int_0 ^ \ infty T〜p（T）〜dT$$

前のシミュレーションでは、選択しました $$$E [T] = \ tau = 10$分。

乗客がバス停にいつでも到着する場合、待ち時間の可能性は、 $$$p（T）$からも $$$T$：間隔が大きいほど、乗客が多くなります。

したがって、乗客の観点から到着時間の分布を書くことができます。

$$

$$p_ {exp}（T）\ propto T〜p（T）$$

比例定数は、分布の正規化から導出されます。

$$

$$p_ {exp}（T）= \ frac {T〜p（T）} {\ int_0 ^ \ infty T〜p（T）〜dT}$$

簡素化する

$$

$$p_ {exp}（T）= \ frac {T〜p（T）} {E [T]}$$

それから待ち時間 $$$E [W]$乗客の予想間隔の半分になるため、記録することができます

$$

$$E [W] = \ frac {1} {2} E_ {exp} [T] = \ frac {1} {2} \ int_0 ^ \ infty T〜p_ {exp}（T）〜dT$$

よりわかりやすい方法で書き換えることができます。

$$

$$E [W] = \ frac {E [T ^ 2]} {2E [T]}$$

そして今では、フォームを選択するだけです $$$p（T）$積分を計算します。

pの選択（T）

正式なモデルを受け取った後、合理的な分布は何ですか $$$p（T）$？ 分布図を描きます $$$p（T）$到着間隔のヒストグラムをプロットすることで、到着のシミュレーションを行います。

 %matplotlib inline import matplotlib.pyplot as plt plt.style.use('seaborn') plt.hist(intervals, bins=np.arange(80), density=True) plt.axvline(intervals.mean(), color='black', linestyle='dotted') plt.xlabel('Interval between arrivals (minutes)') plt.ylabel('Probability density'); 

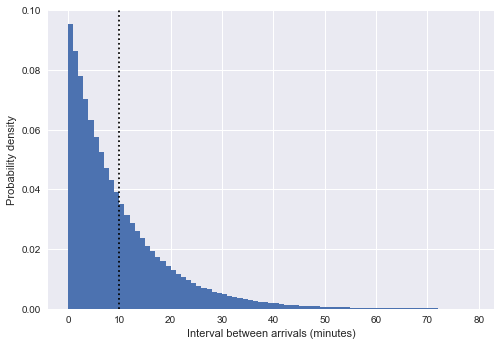
ここで、縦の破線は約10分の平均間隔を示しています。 これは、偶然ではなく、指数分布に非常に似ています：一様乱数の形でのバス到着時間のシミュレーションは、 ポアソン過程に非常に近く、そのような過程では、間隔の分布は指数です。

（注：私たちの場合、これは近似の指数にすぎません;実際には間隔 $$$T$の間に $$$N$期間内で均等に選択されたポイント $$$N \ tau$ベータ分布に一致 $$$T /（N \ tau）\ sim \ mathrm {ベータ} [1、N]$大きな限界にあります $$$N$近づいている $$$T \ sim \ mathrm {Exp} [1 / \ tau]$。 詳細については、たとえばStackExchangeの投稿やTwitterのこの スレッド を ご覧ください ）。

間隔の指数分布は、到着時間がポアソン過程に従うことを意味します。 この推論を検証するために、ポアソンプロセスの別のプロパティの存在を確認します。一定期間の到着数はポアソン分布であるということです。 これを行うために、シミュレートされた到着を時間ブロックに分割します。

 from scipy.stats import poisson # count the number of arrivals in 1-hour bins binsize = 60 binned_arrivals = np.bincount((bus_arrival_times // binsize).astype(int)) x = np.arange(20) # plot the results plt.hist(binned_arrivals, bins=x - 0.5, density=True, alpha=0.5, label='simulation') plt.plot(x, poisson(binsize / tau).pmf(x), 'ok', label='Poisson prediction') plt.xlabel('Number of arrivals per hour') plt.ylabel('frequency') plt.legend(); 

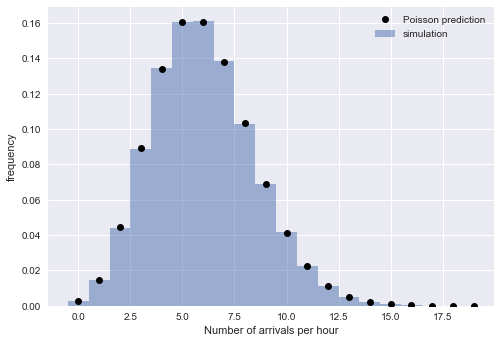
経験値と理論値の密接な対応は、解釈の正確さを確信させます。 $$$N$シミュレートされた到着時間は、指数関数的に分布する間隔を意味するポアソンプロセスによって十分に説明されます。

これは、確率分布を書くことができることを意味します：

$$

$$p（T）= \ frac {1} {\ tau} e ^ {-T / \ tau}$$

前の式の結果を代入すると、ストップでの乗客の平均待ち時間がわかります。

$$

$$E [W] = \ frac {\ int_0 ^ \ infty T ^ 2〜e ^ {-T / \ tau}} {2 \ int_0 ^ \ infty T〜e ^ {-T / \ tau}} = \ frac {2 \ tau ^ 3} {2（\ tau ^ 2）} = \ tau$$

ポアソンプロセスを介して到着するフライトの場合、予想待ち時間は到着間の平均間隔と同じです。

この問題は次のように議論できます。ポアソンプロセスはメモリのないプロセスです。つまり、イベントの履歴は次のイベントの予想時間とは関係ありません。 したがって、バス停に到着すると、バスの平均待ち時間は常に同じです。この場合、前回のバスからどれだけ時間が経過したかに関係なく、10分です。 どれだけ長く待っていても、次のバスまでの予想時間は常に正確に10分です。ポアソンプロセスでは、待っていた時間の「クレジット」は得られません。

現実のタイムアウト

実際のバスの到着が実際にポアソンプロセスによって記述されている場合、上記は適切ですが、そうですか？


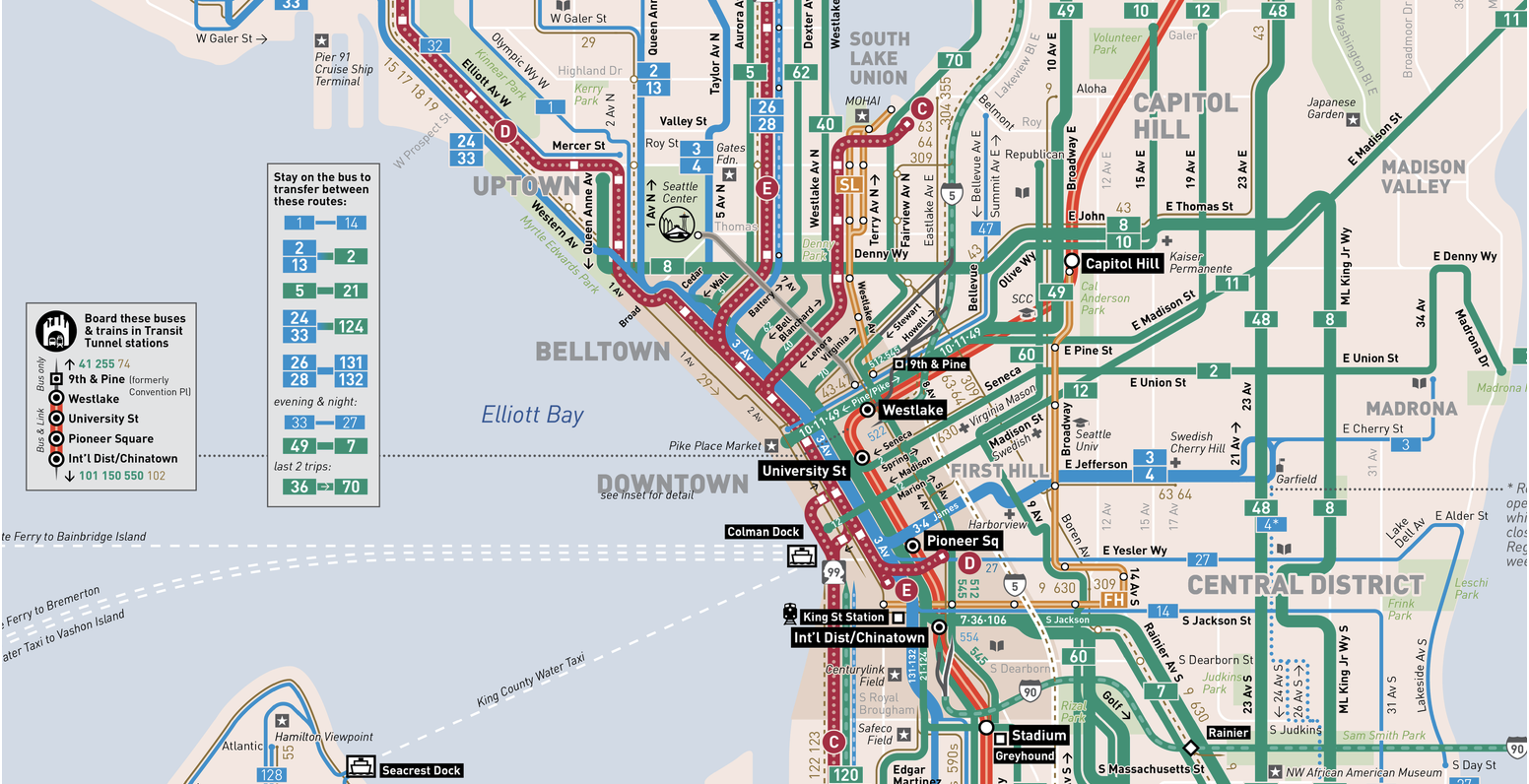出典： シアトル公共交通機関スキーム

待ち時間のパラドックスが現実とどのように一致しているかを判断してみましょう。 これを行うために、ここからダウンロードできるデータのいくつかを調べます。arrival_times.csv （3 MB CSVファイル）。 データセットには、シアトルのダウンタウンにある第3およびパイクバス停でのRapidRideバス C、D、およびEの到着予定時刻と実際の時刻が含まれています。 データは2016年の第2四半期に記録されました（このファイルについては、ワシントン州交通センターのMark Hallenbackに感謝します！）。

 import pandas as pd df = pd.read_csv('arrival_times.csv') df = df.dropna(axis=0, how='any') df.head() 

	OPD_DATE	VEHICLE_ID	RTE	DIR	TRIP_ID	STOP_ID	STOP_NAME	SCH_STOP_TM	ACT_STOP_TM
0	2016-03-26	6201	673	S	30908177	431	3rd AVE＆PIKE ST（431）	01:11:57	01:13:19
1	2016-03-26	6201	673	S	30908033	431	3rd AVE＆PIKE ST（431）	23:19:57	23:16:13
2	2016-03-26	6201	673	S	30908028	431	3rd AVE＆PIKE ST（431）	21:19:57	21:18:46
3	2016-03-26	6201	673	S	30908019	431	3rd AVE＆PIKE ST（431）	19:04:57	19:01:49
4	2016-03-26	6201	673	S	30908252	431	3rd AVE＆PIKE ST（431）	16:42:57	16:42:39

RapidCideデータを選択しました。これは、ほとんどの場合、バスが10〜15分間隔で運行していることを意味します。もちろん、ルートCの頻繁な乗客であるという事実は言うまでもありません。

データクレンジング

まず、便利なビューに変換するために少しデータをクリーニングします。

 # combine date and time into a single timestamp df['scheduled'] = pd.to_datetime(df['OPD_DATE'] + ' ' + df['SCH_STOP_TM']) df['actual'] = pd.to_datetime(df['OPD_DATE'] + ' ' + df['ACT_STOP_TM']) # if scheduled & actual span midnight, then the actual day needs to be adjusted minute = np.timedelta64(1, 'm') hour = 60 * minute diff_hrs = (df['actual'] - df['scheduled']) / hour df.loc[diff_hrs > 20, 'actual'] -= 24 * hour df.loc[diff_hrs < -20, 'actual'] += 24 * hour df['minutes_late'] = (df['actual'] - df['scheduled']) / minute # map internal route codes to external route letters df['route'] = df['RTE'].replace({673: 'C', 674: 'D', 675: 'E'}).astype('category') df['direction'] = df['DIR'].replace({'N': 'northbound', 'S': 'southbound'}).astype('category') # extract useful columns df = df[['route', 'direction', 'scheduled', 'actual', 'minutes_late']].copy() df.head() 

	ルート	方向	グラフ	事実 到着	遅刻（分）
0	C	南	2016-03-26 01:11:57	2016-03-26 01:13:19	1.366667
1	C	南	2016-03-26 23:19:57	2016-03-26 23:16:13	-3.733333
2	C	南	2016-03-26 21:19:57	2016-03-26 21:18:46	-1.183333
3	C	南	2016-03-26 19:04:57	2016-03-26 19:01:49	-3.133333
4	C	南	2016-03-26 16:42:57	2016-03-26 16:42:39	-0.300000

バスは何時までですか？

この表には6つのデータセットがあります。各ルートC、D、およびEの北および南の方向です。それらの特性を理解するために、これら6つのそれぞれの実際のマイナス予定到着時間のヒストグラムを作成します。

 import seaborn as sns g = sns.FacetGrid(df, row="direction", col="route") g.map(plt.hist, "minutes_late", bins=np.arange(-10, 20)) g.set_titles('{col_name} {row_name}') g.set_axis_labels('minutes late', 'number of buses'); 

バスは、ルートの開始時にスケジュールに近く、終了に向かってより多く逸脱すると想定するのが論理的です。 データはこれを確認します。南ルートCと北DおよびEのストップは、ルートの開始点に近く、反対方向-最終目的地から遠くない場所にあります。

スケジュールおよび観測間隔

これらの6つのルートについて、観察されたバス間隔と計画されたバス間隔を見てみましょう。 これらの間隔を計算するために、Pandasのgroupby関数から始めましょう。

 def compute_headway(scheduled): minute = np.timedelta64(1, 'm') return scheduled.sort_values().diff() / minute grouped = df.groupby(['route', 'direction']) df['actual_interval'] = grouped['actual'].transform(compute_headway) df['scheduled_interval'] = grouped['scheduled'].transform(compute_headway) 

 g = sns.FacetGrid(df.dropna(), row="direction", col="route") g.map(plt.hist, "actual_interval", bins=np.arange(50) + 0.5) g.set_titles('{col_name} {row_name}') g.set_axis_labels('actual interval (minutes)', 'number of buses'); 

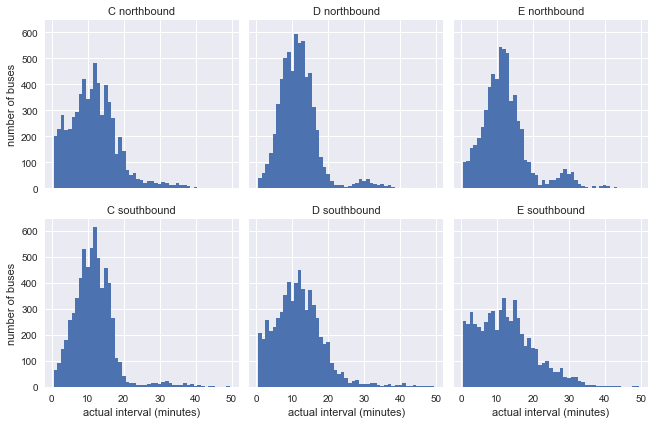
結果がモデルの指数分布とあまり類似していないことはすでに明らかですが、これはまだ何も言っていません。分布はグラフ内の一貫性のない間隔によって影響を受ける可能性があります。

観測された到着間隔ではなく、計画された到着間隔を使用して、ダイアグラムの構築を繰り返しましょう。

 g = sns.FacetGrid(df.dropna(), row="direction", col="route") g.map(plt.hist, "scheduled_interval", bins=np.arange(20) - 0.5) g.set_titles('{col_name} {row_name}') g.set_axis_labels('scheduled interval (minutes)', 'frequency'); 

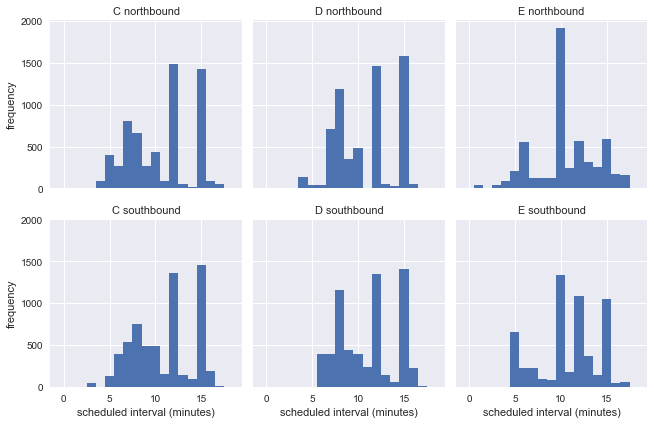
これは、平日はバスが異なる間隔で運行しているため、バス停からの実際の情報を使用して待ち時間パラドックスの精度を推定できないことを示しています。

均一なスケジュールを作成する

公式のスケジュールでは一定の間隔が与えられていませんが、多数のバスがある特定の時間間隔がいくつかあります。たとえば、計画された間隔が10分で約2,000本のEルートバスが北に向かっています。 レイテンシパラドックスが適用可能かどうかを確認するには、データをルート、方向、および計画間隔にグループ化し、それらが順番に発生したかのように再スタックします。 これにより、ソースデータの関連するすべての特性が保持されると同時に、レイテンシパラドックスの予測との直接比較が容易になります。

 def stack_sequence(data): # first, sort by scheduled time data = data.sort_values('scheduled') # re-stack data & recompute relevant quantities data['scheduled'] = data['scheduled_interval'].cumsum() data['actual'] = data['scheduled'] + data['minutes_late'] data['actual_interval'] = data['actual'].sort_values().diff() return data subset = df[df.scheduled_interval.isin([10, 12, 15])] grouped = subset.groupby(['route', 'direction', 'scheduled_interval']) sequenced = grouped.apply(stack_sequence).reset_index(drop=True) sequenced.head() 

	ルート	方向	スケジュール	事実 到着	遅刻（分）	事実 間隔	スケジュールされた間隔
0	C	北	10.0	12.400000	2,400,000	ナン	10.0
1	C	北	20.0	27.150000	7.150000	0.183333	10.0
2	C	北	30.0	26.966667	-3.033333	14.566667	10.0
3	C	北	40.0	35.516667	-4.483333	8.366667	10.0
4	C	北	50.0	53.583333	3.583333	18.066667	10.0

クリアされたデータについて、各ルートと方向に沿ったバスの実際の外観の分布を、到着頻度でスケジュールできます。

 for route in ['C', 'D', 'E']: g = sns.FacetGrid(sequenced.query(f"route == '{route}'"), row="direction", col="scheduled_interval") g.map(plt.hist, "actual_interval", bins=np.arange(40) + 0.5) g.set_titles('{row_name} ({col_name:.0f} min)') g.set_axis_labels('actual interval (min)', 'count') g.fig.set_size_inches(8, 4) g.fig.suptitle(f'{route} line', y=1.05, fontsize=14) 

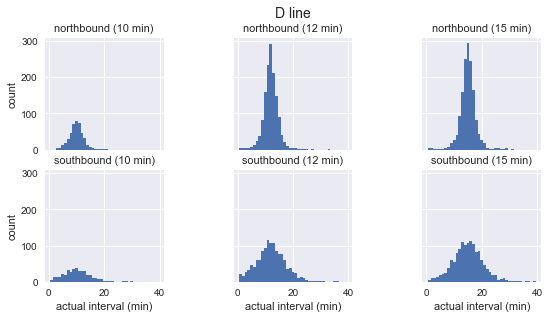
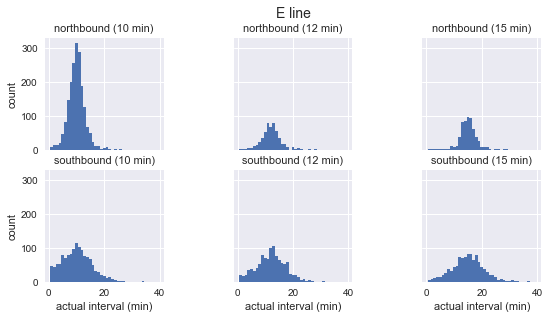
各ルートについて、観測された間隔の分布はほぼガウス分布であることがわかります。 計画された間隔の近くでピークに達し、ルートの開始時（Cの場合は南、D / Eの場合は北）の標準偏差が小さく、終了時の標準偏差が大きくなります。 見た目でも、実際の到着間隔は、指数分布とは明らかに一致しません。これは、待ち時間のパラドックスが基づく主な仮定です。

上記で使用した待ち時間シミュレーション機能を使用して、各バス路線、方向、およびスケジュールの平均待ち時間を見つけることができます。

 grouped = sequenced.groupby(['route', 'direction', 'scheduled_interval']) sims = grouped['actual'].apply(simulate_wait_times) sims.apply(lambda times: "{0:.1f} +/- {1:.1f}".format(times.mean(), times.std())) 

 ルート方向のスケジュール間隔
 C北10.0 7.8 +/- 12.5
                       12.0 7.4 +/- 5.7
                       15.0 8.8 +/- 6.4
         南10.0 6.2 +/- 6.3
                       12.0 6.8 +/- 5.2
                       15.0 8.4 +/- 7.3
北部10.0 6.1 +/- 7.1
                       12.0 6.5 +/- 4.6
                       15.0 7.9 +/- 5.3
         南10.0 6.7 +/- 5.3
                       12.0 7.5 +/- 5.9
                       15.0 8.8 +/- 6.5
北10.0 5.5 +/- 3.7
                       12.0 6.5 +/- 4.3
                       15.0 7.9 +/- 4.9
         南10.0 6.8 +/- 5.6
                       12.0 7.3 +/- 5.2
                       15.0 8.7 +/- 6.0
名前：actual、dtype：object 

平均待機時間（おそらく1〜2分）は、計画間隔の半分以上ですが、待機時間のパラドックスが示すように、計画間隔とは異なります。 つまり、検査のパラドックスは確認されますが、待機時間のパラドックスは正しくありません。

おわりに

レイテンシパラドックスは、モデリング、確率理論、統計的仮定と現実の比較を含む議論の興味深い出発点でした。 現実の世界では、バス路線はある種の検査パラドックスに従うことを確認していますが、上記の分析は非常に説得力のあることを示しています。待ち時間のパラドックスの根底にある主な仮定-バスの到着はポアソン過程の統計に従う-は正当化されません。

振り返ってみると、これは驚くことではありません。ポアソンプロセスは、到着の確率が前回の到着からの時間とは完全に独立していると仮定するメモリレスプロセスです。 実際、適切に管理された公共交通システムには、この動作を回避するために特別に構成された時刻表があります。バスは、日中はランダムな時間にルートを開始せず、乗客の最も効率的な輸送のために選択されたスケジュールに従って開始します。

より重要な教訓は、データ分析タスクについて行う仮定に注意することです。 場合によっては、ポアソンプロセスが到着時間データの適切な説明になることがあります。 しかし、あるデータ型が別のデータ型のように聞こえるからといって、一方に有効な仮定がもう一方にも有効であるとは限りません。 多くの場合、正しいと思われる仮定は、真実ではない結論につながる可能性があります。