
最も典型的な物理モデルの例では、関数を操作するスキルを統合し、Matplotlib Pythonのすべてのパワーを提供する、高速で便利で美しいPyPlotビジュアライザーに精通します。 たくさんの写真があります(ネタバレの下に隠れています)
ボンネットの下ですべてが清潔で新鮮であることを確認します。
ボンネットの下]status Status `C:\Users\\.julia\environments\v1.0\Project.toml` [537997a7] AbstractPlotting v0.9.0 [ad839575] Blink v0.8.1 [159f3aea] Cairo v0.5.6 [5ae59095] Colors v0.9.5 [8f4d0f93] Conda v1.1.1 [0c46a032] DifferentialEquations v5.3.1 [a1bb12fb] Electron v0.3.0 [5789e2e9] FileIO v1.0.2 [5752ebe1] GMT v0.5.0 [28b8d3ca] GR v0.35.0 [c91e804a] Gadfly v1.0.0+ #master (https://github.com/GiovineItalia/Gadfly.jl.git) [4c0ca9eb] Gtk v0.16.4 [a1b4810d] Hexagons v0.2.0 [7073ff75] IJulia v1.13.0+ [`C:\Users\\.julia\dev\IJulia`] [6218d12a] ImageMagick v0.7.1 [c601a237] Interact v0.9.0 [b964fa9f] LaTeXStrings v1.0.3 [ee78f7c6] Makie v0.9.0+ #master (https://github.com/JuliaPlots/Makie.jl.git) [7269a6da] MeshIO v0.3.1 [47be7bcc] ORCA v0.2.0 [58dd65bb] Plotly v0.2.0 [f0f68f2c] PlotlyJS v0.12.0+ #master (https://github.com/sglyon/PlotlyJS.jl.git) [91a5bcdd] Plots v0.21.0 [438e738f] PyCall v1.18.5 [d330b81b] PyPlot v2.6.3 [c4c386cf] Rsvg v0.2.2 [60ddc479] StatPlots v0.8.1 [b8865327] UnicodePlots v0.3.1 [0f1e0344] WebIO v0.4.2 [c2297ded] ZMQ v1.0.0
そうでなければ、今日必要なものはすべて手に入ります julia>] pkg> add PyCall pkg> add LaTeXStrings pkg> add PyPlot pkg> build PyPlot # build # - , pkg> add Conda # Jupyter - pkg> add IJulia # pkg> build IJulia # build
さあ、タスクへ!
輸送方程式
物理学では、転送という用語は不可逆プロセスを意味すると理解されており、その結果、物理システムで質量、運動量、エネルギー、電荷、またはその他の物理量の空間的移動(転送)が発生します。
線形1次元輸送方程式(または移流方程式)-最も単純な偏微分方程式-は、
輸送方程式の数値解法には、明示的な差分スキームを使用できます。
どこで -上位タイムレイヤーのグリッド関数の値。 この回路はクーラント数で安定しています。
非線形転送
ラインソース(吸収移動): 。 明示的な差分スキームを使用します。
using Plots pyplot() a = 0.2 b = 0.01 ust = x -> x^2 * exp( -(xa)^2/b ) # bord = t -> 0. # # - function transferequi(;C0 = 1., C1 = 0., B = 0., Nx = 50, Nt = 50, tlmt = 0.01) dx = 1/Nx dt = tlmt/Nt b0 = 0.5B*dt c0 = C0*dt/dx c1 = C1*dt/dx print("Kurant: $c0 $c1") x = [i for i in range(0, length = Nx, step = dx)]# t = [i for i in range(0, length = Nt, step = dt)] # - U = zeros(Nx, Nt) U[:,1] = ust.(x) U[1,:] = bord.(t) for j = 1:Nt-1, i = 2:Nx U[i, j+1] = ( 1-b0-c0-c1*U[i,j] )*U[i,j] + ( c0-b0+c1*U[i,j] )*U[i-1,j] end t, x, U end t, X, Ans0 = transferequi( C0 = 4., C1 = 1., B = 1.5, tlmt = 0.2 ) plot(X, Ans0[:,1], lab = "t1") plot!(X, Ans0[:,10], lab = "t10") p = plot!(X, Ans0[:,40], lab = "t40") plot( p, heatmap(t, X, Ans0) ) #
吸収を強化する:
t, X, Ans0 = transferequi( C0 = 2., C1 = 1., B = 3.5, tlmt = 0.2 ) plot(X, Ans0[:,1]) plot!(X, Ans0[:,10]) p = plot!(X, Ans0[:,40]) plot( p, heatmap(t, X, Ans0) )
t, X, Ans0 = transferequi( C0 = 1., C1 = 15., B = 0.1, Nx = 100, Nt = 100, tlmt = 0.4 ) plot(X, Ans0[:,1]) plot!(X, Ans0[:,20]) plot!(X, Ans0[:,90])
ほぼ倒れた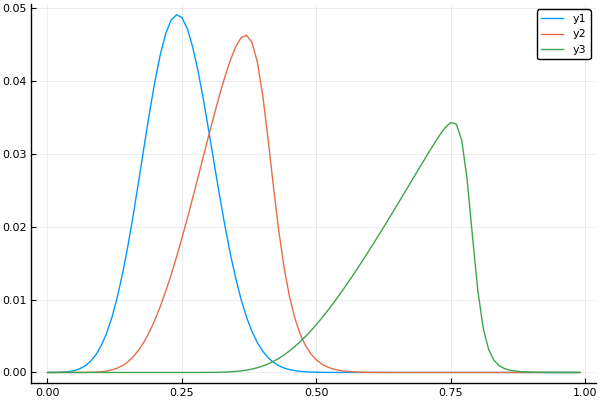
heatmap(t, X, Ans0)
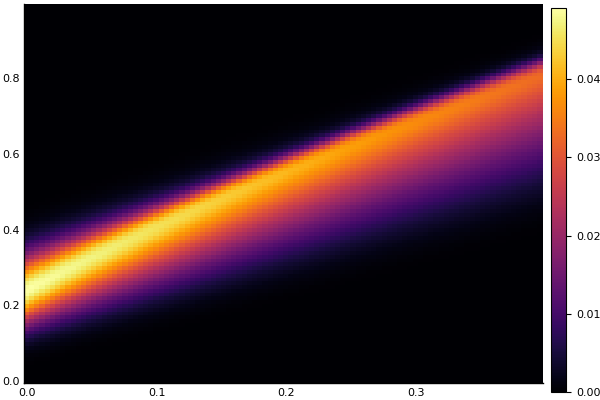
熱方程式
示差熱方程式(または熱拡散方程式)は、次のように記述されます。
これは、時間tに関する1次導関数と空間座標xに関する2次導関数を含む放物線方程式です。 たとえば、冷却または加熱用の金属棒の温度ダイナミクスを表します(関数Tは、棒に沿ったx座標に沿った温度プロファイルを表します)。 係数Dは、熱伝導率(拡散)と呼ばれます。 座標と、目的の関数D(t、x、T)自体の両方に明示的に依存するか、定数にすることができます。
線形方程式を考えます(拡散係数と熱源は温度に依存しません)。 それぞれ明示的および暗黙的なオイラースキームを使用した微分方程式の差分近似:
δ(x) = x==0 ? 0.5 : x>0 ? 1 : 0 # - startcond = x-> δ(x-0.45) - δ(x-0.55) # bordrcond = x-> 0. # D(u) = 1 # Φ(u) = 0 # # LaTex Tab # \delta press Tab -> δ function linexplicit(Nx = 50, Nt = 40; tlmt = 0.01) dx = 1/Nx dt = tlmt/Nt k = dt/(dx*dx) print("Kurant: $k dx = $dx dt = $dt k<0.5? $(k<0.5)") x = [i for i in range(0, length = Nx, step = dx)] # t = [i for i in range(0, length = Nt, step = dt)] # - U = zeros(Nx, Nt) U[: ,1] = startcond.(x) U[1 ,:] = U[Nt,:] = bordrcond.(t) for j = 1:Nt-1, i = 2:Nx-1 U[i, j+1] = U[i,j]*(1-2k*D( U[i,j] )) + k*U[i-1,j]*D( U[i-1,j] ) + k*U[i+1,j]*D( U[i+1,j] ) + dt*Φ(U[i,j]) end t, x, U end t, X, Ans2 = linexplicit( tlmt = 0.005 ) plot(X, Ans2[:,1], lab = "t1") plot!(X, Ans2[:,10], lab = "t10") p = plot!(X, Ans2[:,40], lab = "t40", title = "Explicit scheme") plot( p, heatmap(t, X, Ans2) )
暗黙的なスキームとスイープ方法を使用します function nonexplicit(Nx = 50, Nt = 40; tlmt = 0.01) dx = 1/Nx dt = tlmt/Nt k = dt/(dx*dx) print("Kurant: $k dx = $dx dt = $dt k<0.5? $(k<0.5)\n") x = [i for i in range(0, length = Nx, step = dx)] t = [i for i in range(0, length = Nt, step = dt)] U = zeros(Nx, Nt) η = zeros(Nx+1) ξ = zeros(Nx) U[: ,1] = startcond.(x) U[1 ,:] = bordrcond.(t) U[Nt,:] = bordrcond.(t) for j = 1:Nt-1 b = -1 - 2k*D( U[1,j] ) c = -k*D( U[2,j] ) d = U[1,j] + dt*Φ(U[1,j]) ξ[2] = c/b η[2] = -d/b for i = 2:Nx-1 a = -k*D( U[i-1,j] ) b = -2k*D( U[i,j] ) - 1 c = -k*D( U[i+1,j] ) d = U[i,j] + dt*Φ(U[i,j]) ξ[i+1] = c / (ba*ξ[i]) η[i+1] = (a*η[i]-d) / (ba*ξ[i]) end U[Nx,j+1] = η[Nx] for i = Nx:-1:2 U[i-1,j+1] = ξ[i]*U[i,j+1] + η[i] end end t, x, U end plot(X, Ans2[:,1], lab = "ex_t1") plot!(X, Ans2[:,10], lab = "ex_t10") plot!(X, Ans2[:,40], lab = "ex_t40") plot!(X, Ans3[:,1], lab = "non_t1") plot!(X, Ans3[:,10], lab = "non_t10") plot!(X, Ans3[:,40], lab = "non_t40", title = "Comparison schemes")
非線形熱方程式
たとえば、非線形熱源を使用して、非線形熱方程式のさらに興味深い解を得ることができます 。 この形式で設定すると、一次加熱ゾーンの両側に伝播するサーマルフロントの形式のソリューションが得られます。
Φ(u) = 1e3*(uu^3) t, X, Ans4 = linexplicit( tlmt = 0.005 ) plot(X, Ans4[:,1], lab = "ex_t1") plot!(X, Ans4[:,10], lab = "ex_t10") plot!(X, Ans4[:,40], lab = "ex_t40", title = "Thermal front")
拡散係数の非線形性により、さらに予想外の解決策も可能です。 たとえば、あなたが取る場合 、 、その後、一次加熱の領域に局所化された媒体の燃焼の影響を観察できます(「悪化を伴う」Sモード燃焼)。
同時に、ソースと拡散係数の両方の非線形性で暗黙的なスキームがどのように機能するかを確認します
D(u) = u*u Φ(u) = 1e3*abs(u)^(3.5) t, X, Ans5 = linexplicit( tlmt = 0.0005 ) t, X, Ans6 = nonexplicit( tlmt = 0.0005 ) plot(X, Ans5[:,1], lab = "ex_t1") plot!(X, Ans5[:,10], lab = "ex_t10") p1 = plot!(X, Ans5[:,40], lab = "ex_t40", title = "Burning with aggravation") p2 = heatmap(abs.(Ans6-Ans5), title = "Difference") # plot(p1, p2)
波動方程式
双曲線方程式
は、分散のない1次元の線形波を表します。 たとえば、弦の振動、液体(気体)の音、真空中の電磁波(後者の場合、方程式はベクトル形式で記述する必要があります)。
この方程式を近似する最も単純な差分スキームは、明示的な5点スキームです。
「クロス」と呼ばれるこの方式は、時間と空間座標の精度が2次であり、時間は3層です。
# ψ = x -> x^2 * exp( -(x-0.5)^2/0.01 ) # ϕ(x) = 0 c = x -> 1 # function pdesolver(N = 100, K = 100, L = 2pi, T = 10, a = 0.1 ) dx = L/N; dt = T/K; gam(x) = c(x)*c(x)*a*a*dt*dt/dx/dx; print("Kurant-Fridrihs-Levi: $(dt*a/dx) dx = $dx dt = $dt") u = zeros(N,K); x = [i for i in range(0, length = N, step = dx)] # u[:,1] = ψ.(x); u[:,2] = u[:,1] + dt*ψ.(x); # fill!( u[1,:], 0); fill!( u[N,:], ϕ(L) ); for t = 2:K-1, i = 2:N-1 u[i,t+1] = -u[i,t-1] + gam( x[i] )* (u[i-1,t] + u[i+1,t]) + (2-2*gam( x[i] ) )*u[i,t]; end x, u end N = 50; # K = 40; # a = 0.1; # L = 1; # T = 1; # t = [i for i in range(0, length = K, stop = T)] X, U = pdesolver(N, K, L, T, a) # plot(X, U[:,1]) plot!(X, U[:,40])
サーフェスを構築するには、PyPlotをPlots環境として使用しますが、直接:
表面グラフ using PyPlot surf(t, X, U)
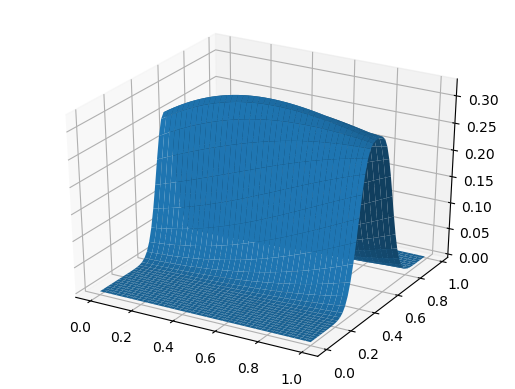
また、デザートの場合、波は座標依存の速度で伝播します。
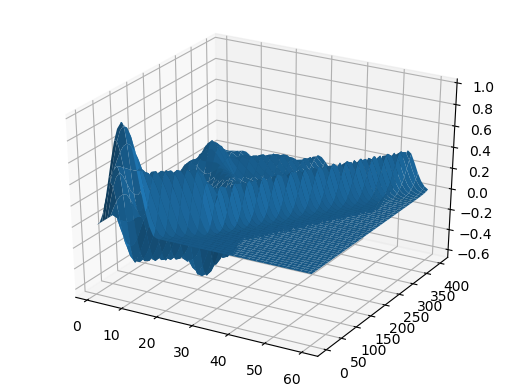
ψ = x -> x>1/3 ? 0 : sin(3pi*x)^2 c = x -> x>0.5 ? 0.5 : 1 X, U = pdesolver(400, 400, 8, 1.5, 1) plot(X, U[:,1]) plot!(X, U[:,40]) plot!(X, U[:,90]) plot!(X, U[:,200], xaxis=(" ", (0, 1.5), 0:0.5:2) )
結果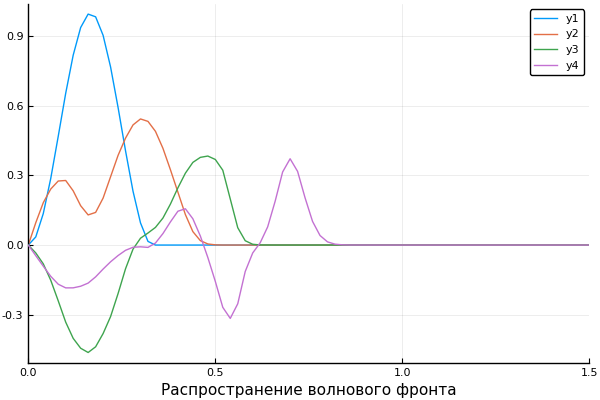
U2 = [ U[i,j] for i = 1:60, j = 1:size(U,2) ]
heatmap(U, yaxis=(" ", (0, 50), 0:10:50))
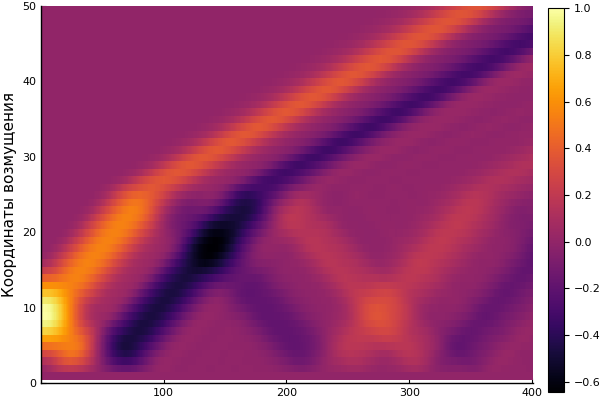
今日はこれで十分です。 より詳細なレビュー:
PyPlotはgithubへのリンク 、環境としての Plot の使用例、およびJuliaによるロシア語の良いメモです。