油圧ラインの波のプロセス。 基本

こんにちは、Habr！

前回の記事では、油圧ラインの波のプロセスを計算するために設計された特性の方法について説明しました。 実際、波のプロセスは心の中で計算できます。アプローチを知るだけで十分です。

カットの下に、「指で」表示し、gifを使用して主な波の効果を示します。 例として、再び油圧ラインを使用しますが、実際には、それらは音響および電気ラインとほぼ同じ方程式に基づいています。 そのため、水力学ではない場合でも、波のプロセス全般を理解するのに役立つ簡単なアナロジーがあります。

ご注意 猫の下で15 MBのアニメーションGIF！

そのため、ここでは、油圧ラインでの1次元平面波の伝播について検討します。 この仮定は、長さが内径よりも何倍も長い長いパイプラインには非常に当てはまります。 簡単にするために、簡単にするために摩擦も無視します。 この場合、進行中の物理プロセスは、1組の偏微分方程式で記述されます。

$$

$$\ frac {\ partial p} {\ partial t} + \ rho \; c ^ 2 \ frac {\ partial v} {\ partial x} = 0$$

$$

$$\ frac {\ partial v} {\ partial t} + \ frac1 \ rho \ frac {\ displaystyle \ partial p} {\ displaystyle \ partial x} = 0$$

どこで $$$\ rho$-密度 $$$v$-速度 $$$p$-圧力 $$$c$音速です。

習慣から、これらの方程式の外観は恐ろしいことがありますが、実際、ここではすべてが簡単です。 最初の方程式は、パイプセグメントに流出するよりも多くの液体が流入すると圧力が時間とともに増加することを示しています（さらに、液体がパイプ内でより高密度で弾性があるほど速くなります）。 2番目の式は、液体のセグメントを加速するために、圧力差を適用する必要があることを示しています（さらに、密度が大きいほど、セグメントを加速するために圧力差を適用する必要があります）。 つまり 非常にありふれたものが記述されています。流体は圧縮可能であり、流体には質量があります。
これらの方程式の解析解を将来の記事のために残して、すぐに「指で」の例に渡しましょう。
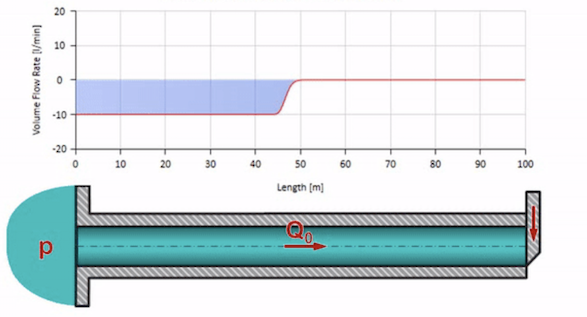
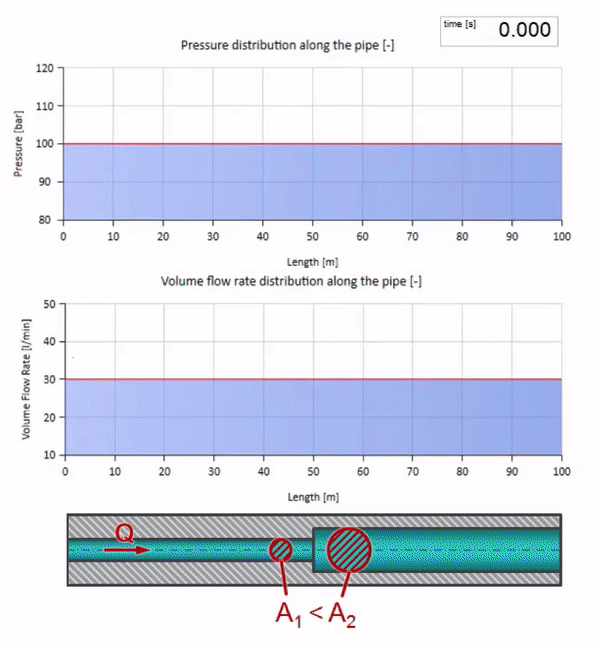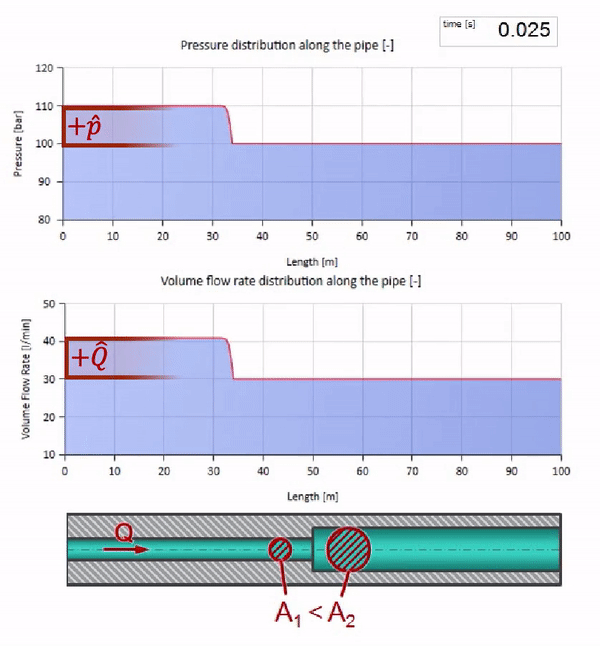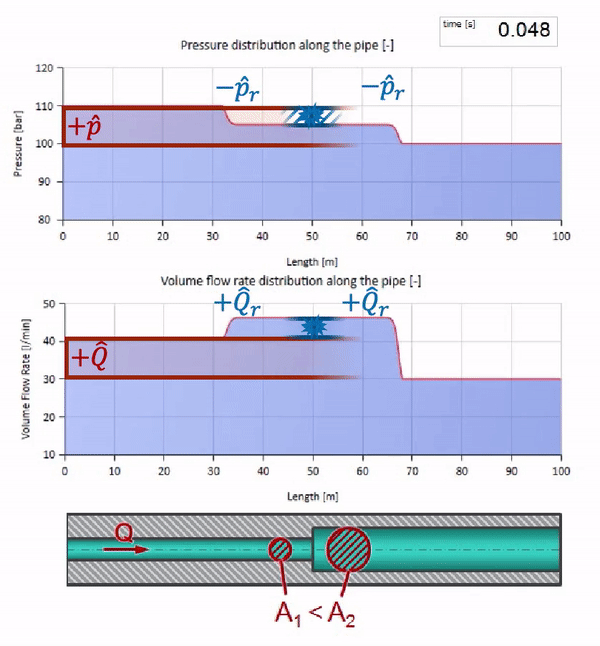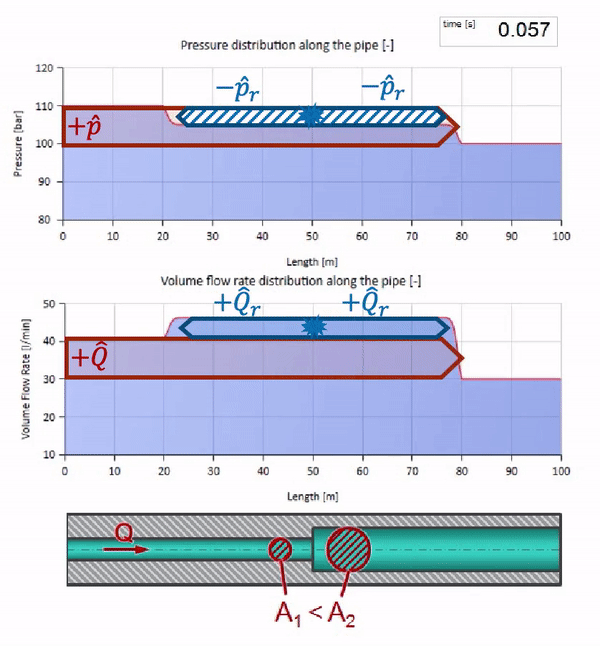
100 bar（10 MPa）の圧力が維持され、30 l / minの流量が流れる水で満たされたパイプを使用します。 圧力のステップが左端に適用されると、メディア内の音の速度に等しい速度でストリームに沿って動き始めることが予測できます。

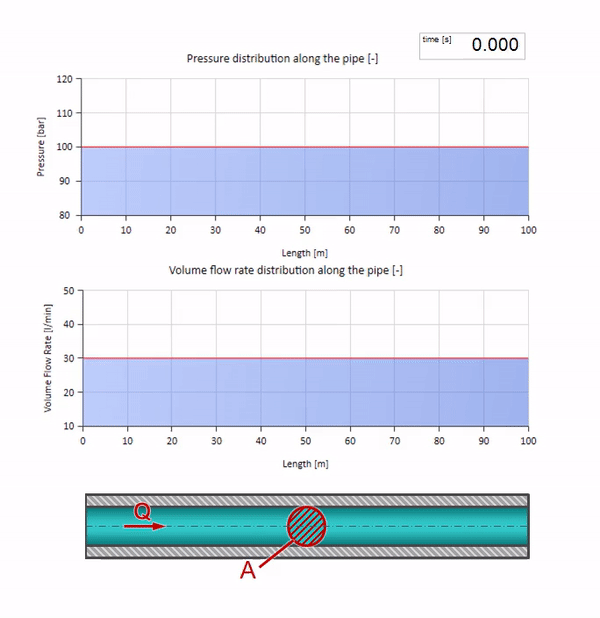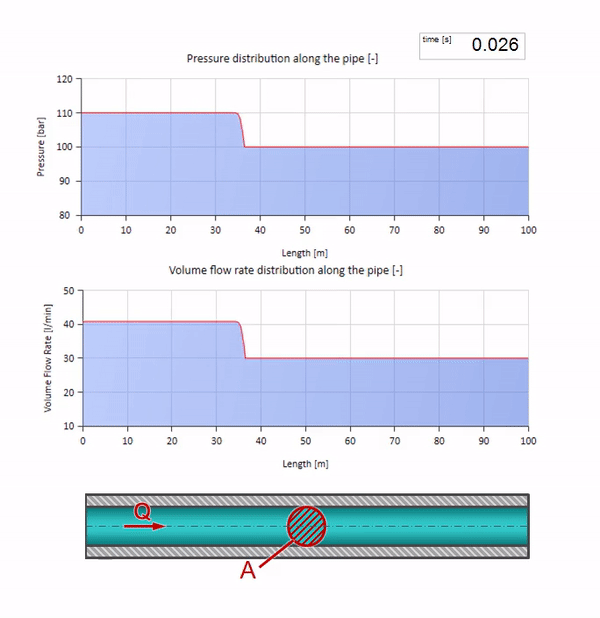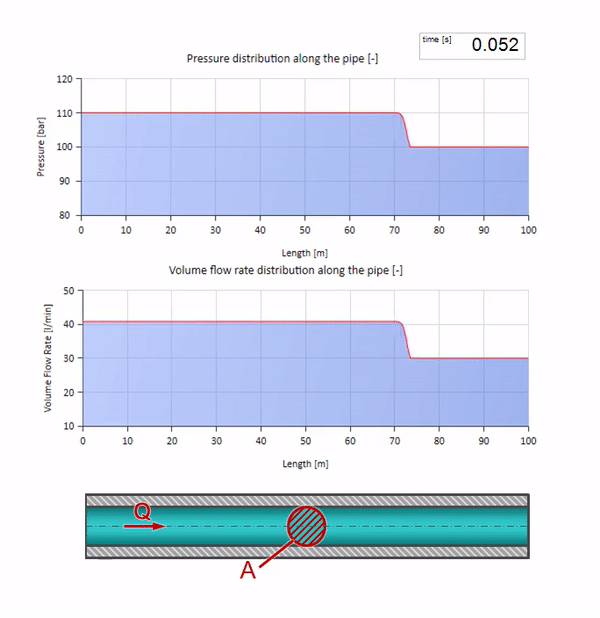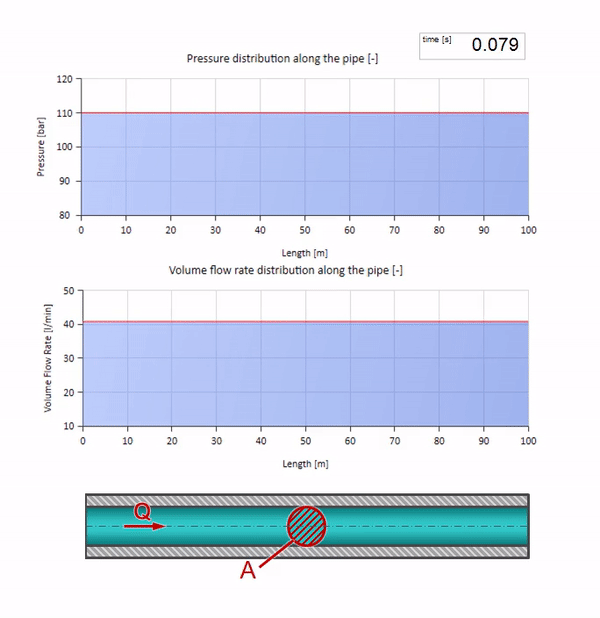
もちろん、圧力により流量も変化します。 圧力が上昇すると、上流の液体が「調整」され、流量も「ステップ」だけ増加します。 波動インピーダンスの値によって決定される量。 断面積のあるパイプの場合 $$$A$密度液体で満たされた $$$\ rho$音のローカル速度 $$$c$、波動インピーダンスは次のように計算できます。

$$

$$Z_L = \ frac {\ rho \; c} A$$

寸法に関しては、これは従来の油圧抵抗と同じであり、圧力波比（ $$$\ widehat p$）および流量（ $$$\ワイドハットQ$）、および絶対値ではありません：

$$

$$Z_L = \ frac {\ widehat p} {\ widehat Q}$$

音の密度と速度が高いほど、波のインピーダンスが高くなります。 特定の圧力降下で液体が分散するのがより困難になります（流量を増やす）

次に、2つの波が互いに向かって移動する様子を見てみましょう。

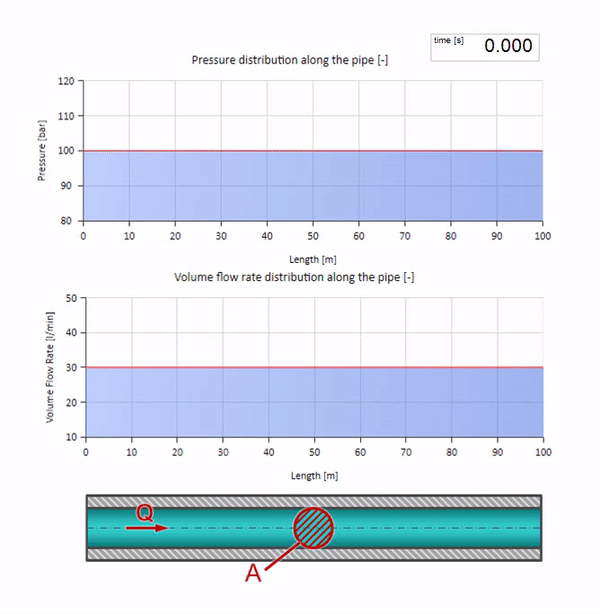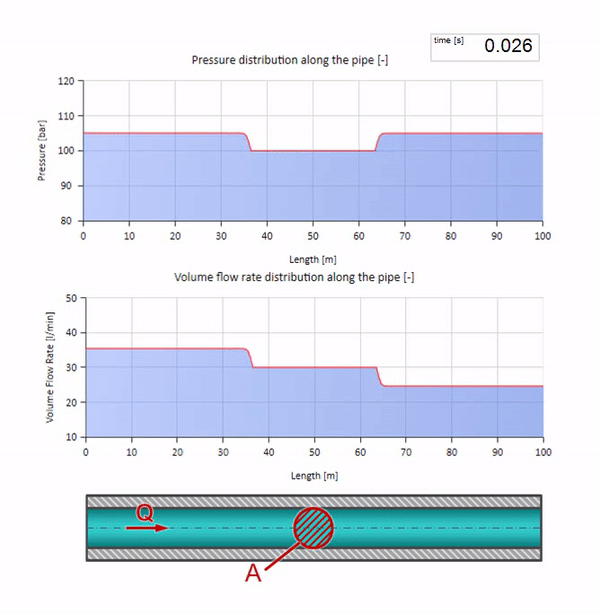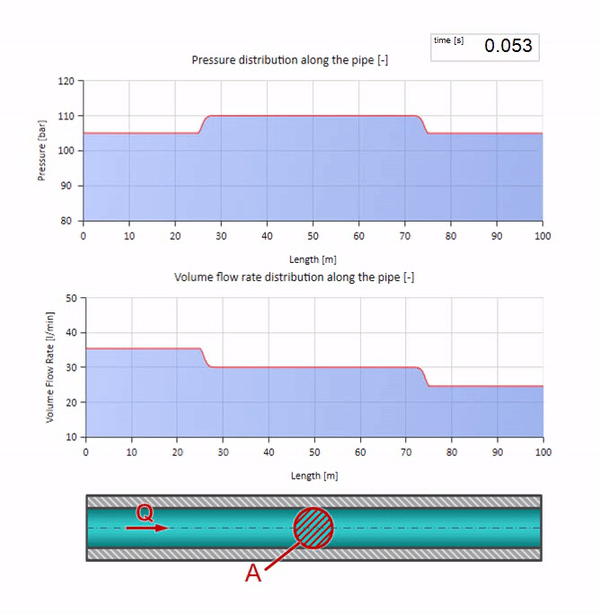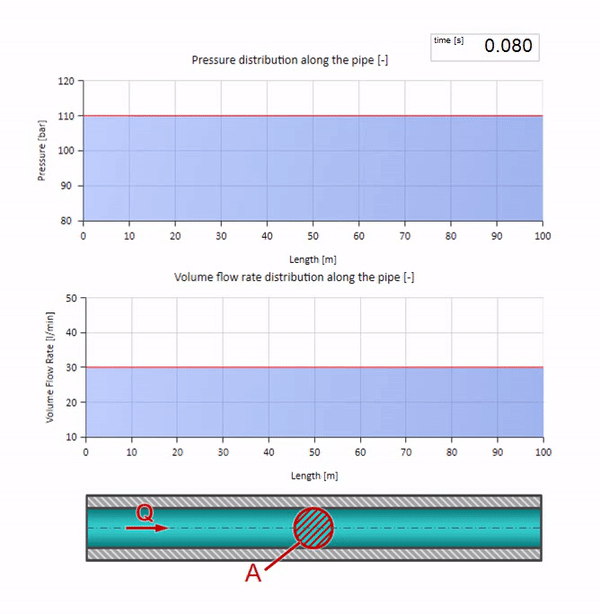
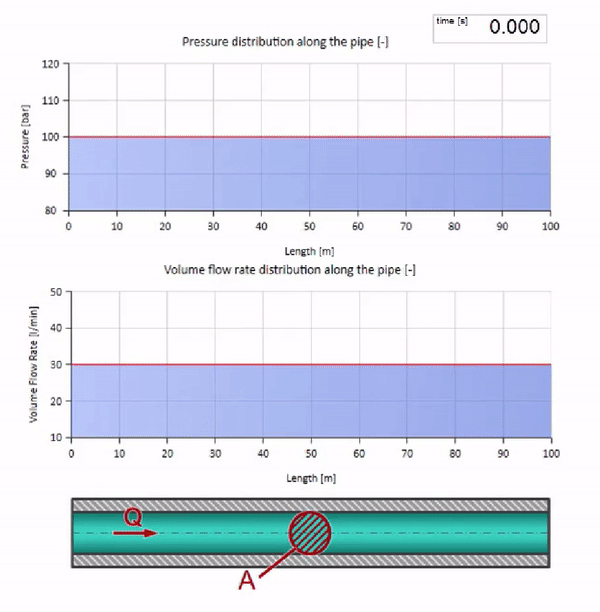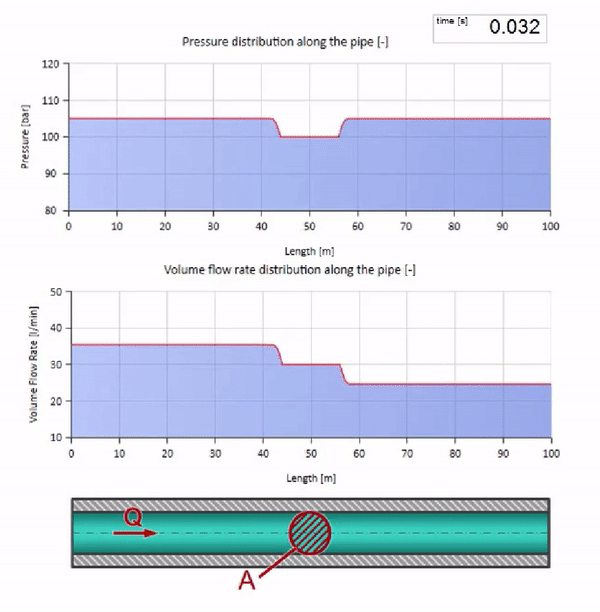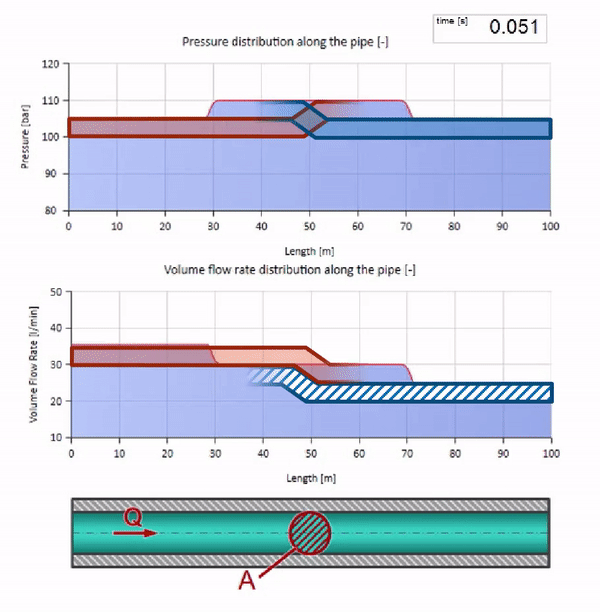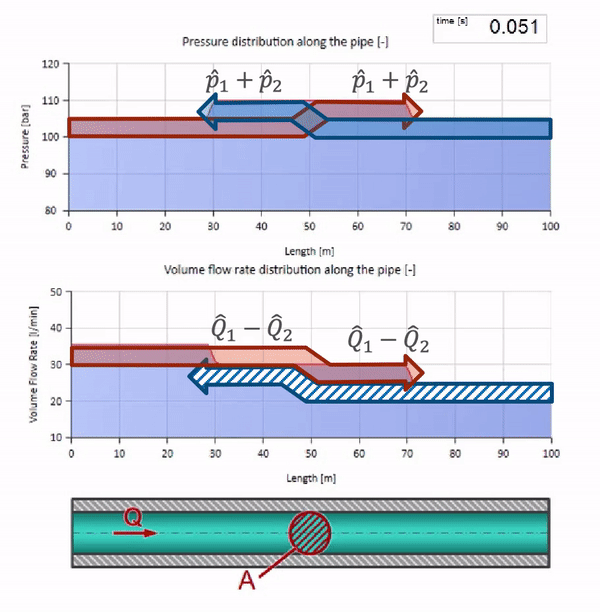
右端の圧力が上昇すると、流体は負の差によって必然的に抑制されます。 これは、流れに逆らう圧力増加波が、波の抵抗によって再び決定される量だけ流量が減少することを意味します。 つまり、圧力の増加と流れの下降の波が右側に移動します。
衝突では、流れの波が互いに反射して戻ってくるように見える場合があります。 実際、それらは単純に重なり合っています。 この効果は干渉とも呼ばれます。

これで、液体を含むすべてのパイプには、耐波性などの特性があることがわかりました。 特定のセクションのパイプの直径が劇的に変化した場合、波に何が起こるかを見るのは興味深いです：

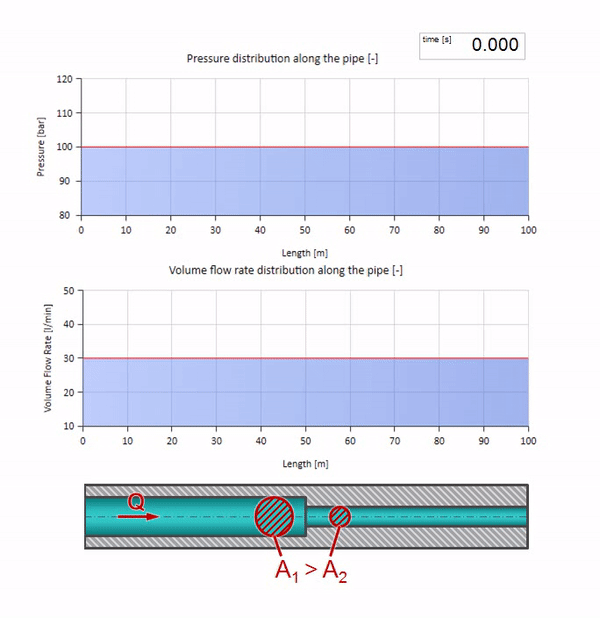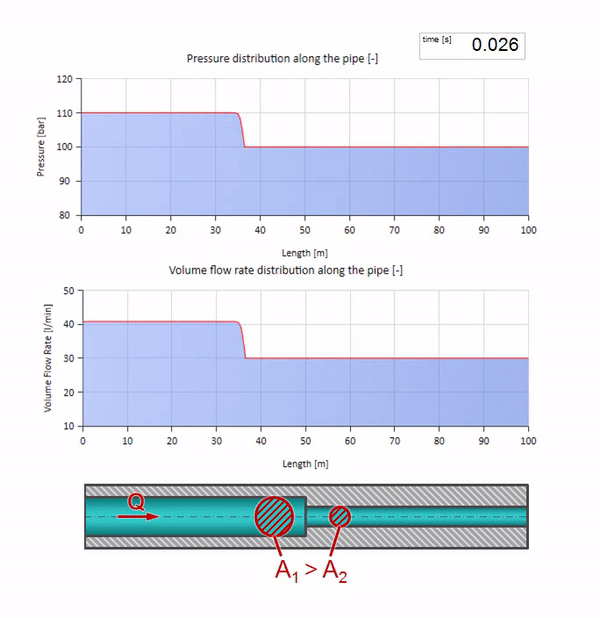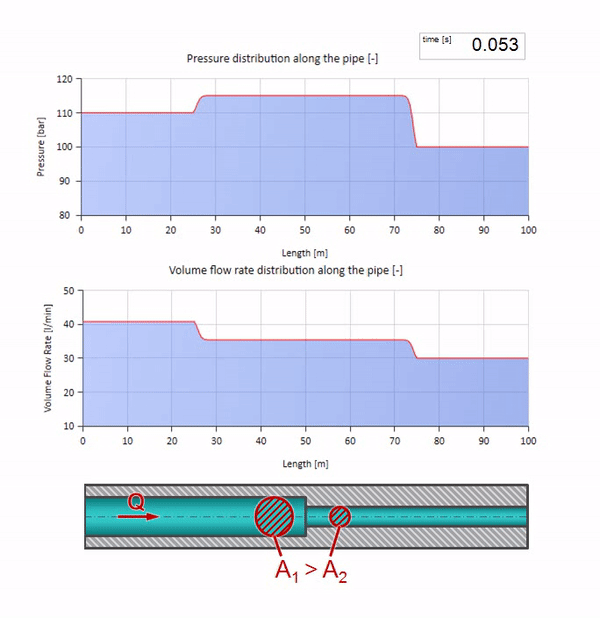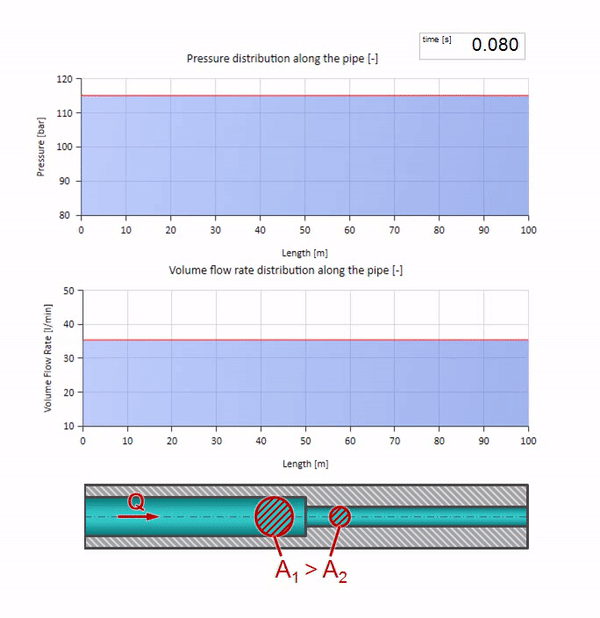
もちろん、パイプの直径が小さくなった場所に波が到達する前に、興味深いことは何も起こりません。 しかし、その後、波のインピーダンスがより高いセクションに到達します。つまり、圧力波と流れの波の比率は、パイプの左側のセクションよりも大きくする必要があります。 これは、圧力波が増加し、流量が減少することを意味します。 同時に、2つのパイプの接合部で同じ値を維持しながら、左に曲がること以外、波に残されたものはありません。

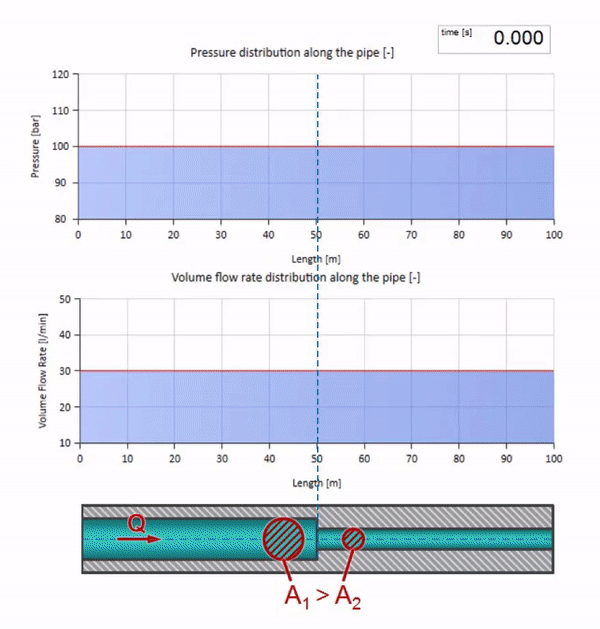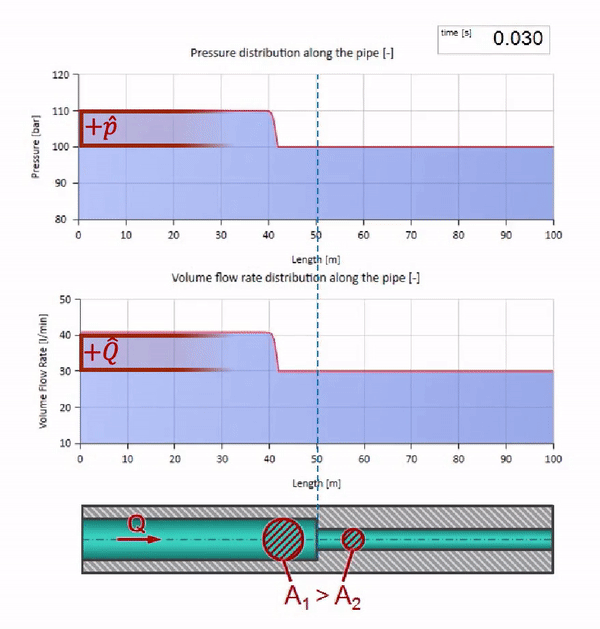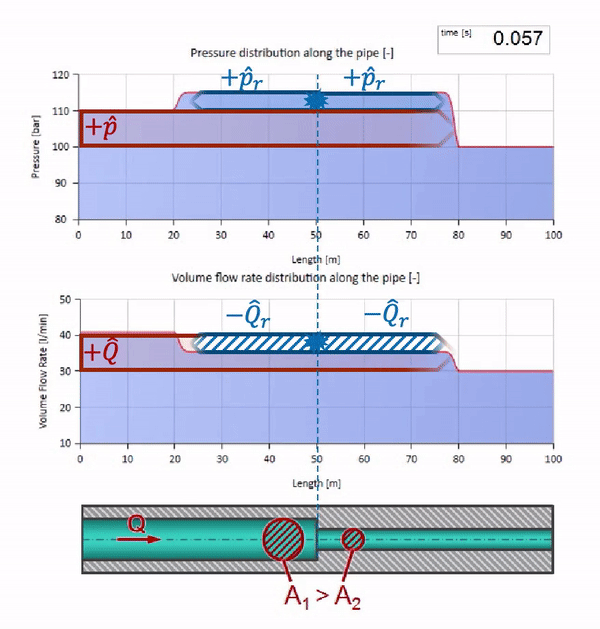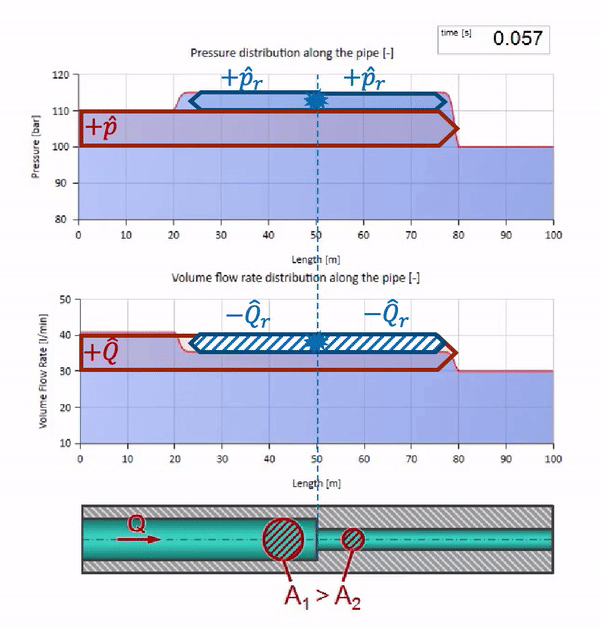
計算には、反射係数を使用すると便利です $$$r$、個々のセクションの波動インピーダンスから考慮されます：

$$

$$r = \ frac {Z_2-Z_1} {Z_1 + Z_2}$$

次に、圧力と流れの反射波を次のように計算できます。

$$

$${\ widehat p} _r = r \; \ widehat p$$

$$

$${\ widehat Q} _r =-\ frac {\ displaystyle \; {\ widehat p} _r} {Z_1} =-r \; \ widehat Q$$

これらの波自体は、元の波との干渉の法則に従って重畳されます。
そして、それはより低い波の抵抗を持つサイトからの波の反射の写真のように見えます：

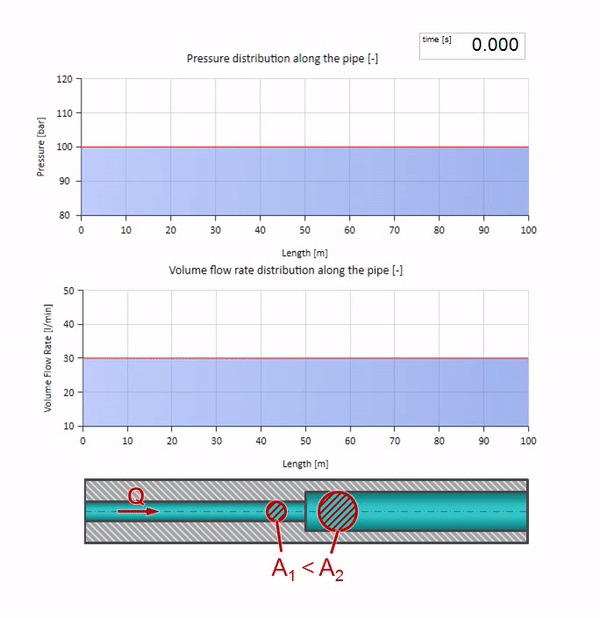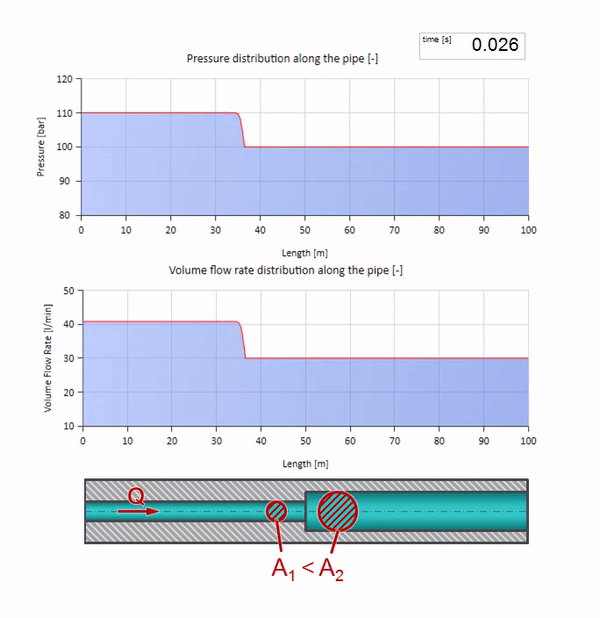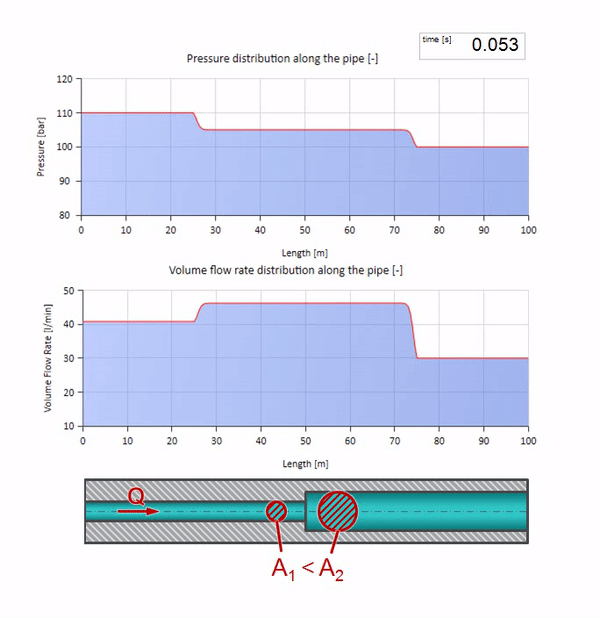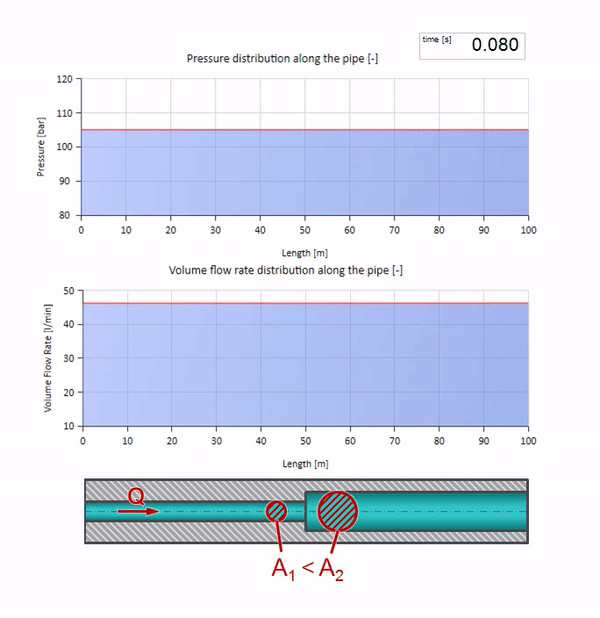
今回は、反射係数が負であることがわかります。これは、反射後の圧力波が少なくなり、逆に流量が大きくなることを意味します。

インピーダンスはパイプのサイズだけでなく、局所的な音速にも依存することを覚えておく必要があります。 つまり 音速がはるかに低いゴム製スリーブのパイプセクションがある場合、波も反射されます。

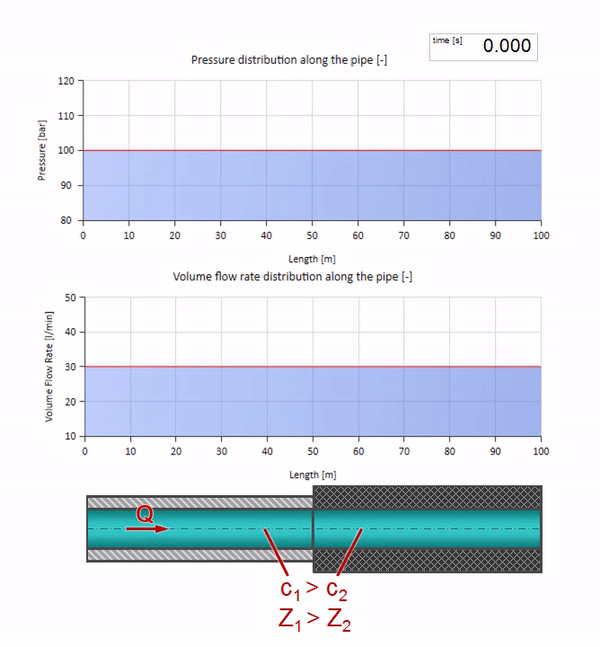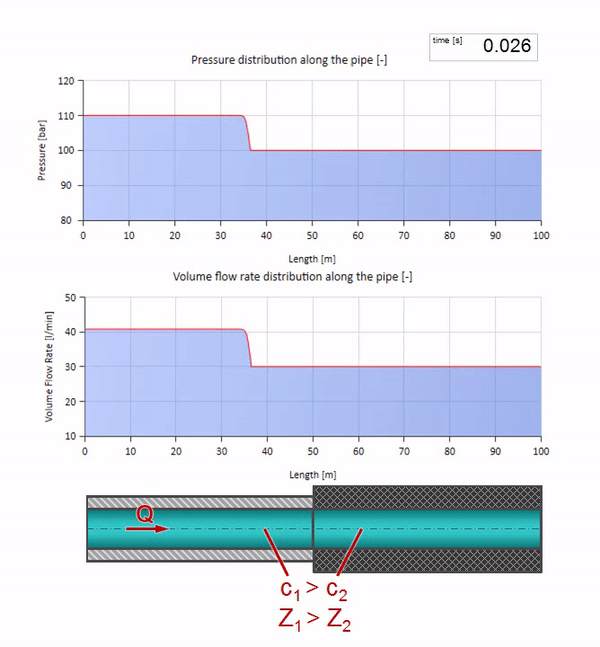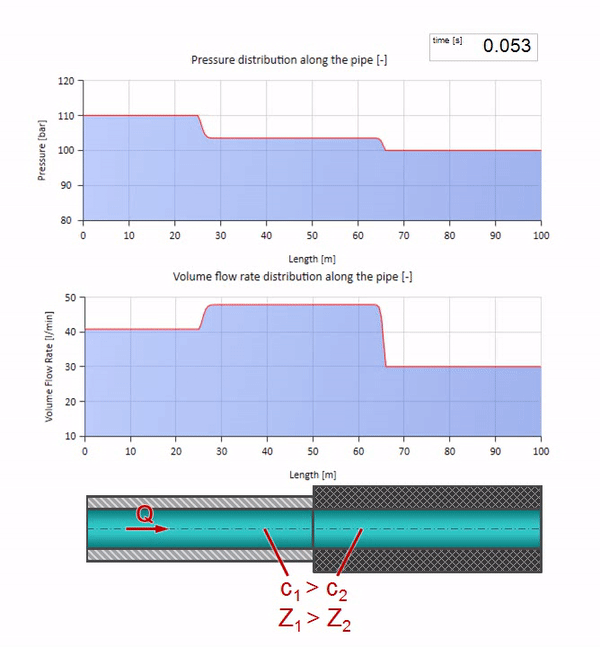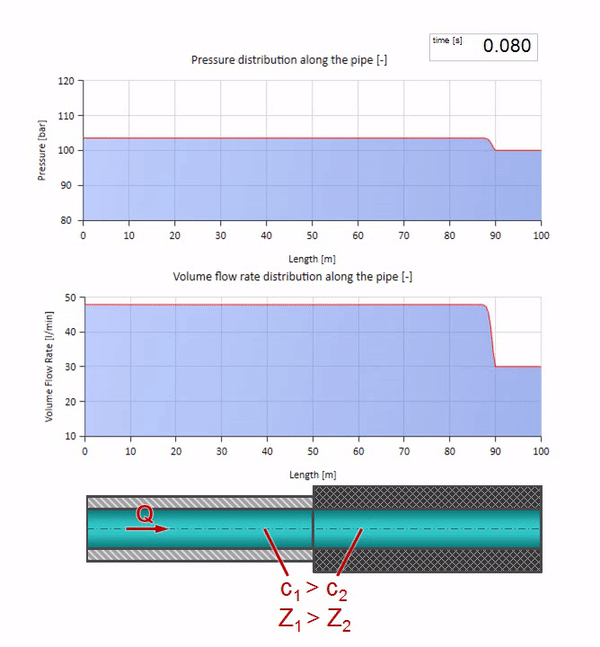
第一に、パイプのゴム壁があるセクションの波がよりゆっくりと移動することがすぐにわかります。 そして、波の抵抗が低いため、反射の結果はパイプの拡張の場合に似ています：

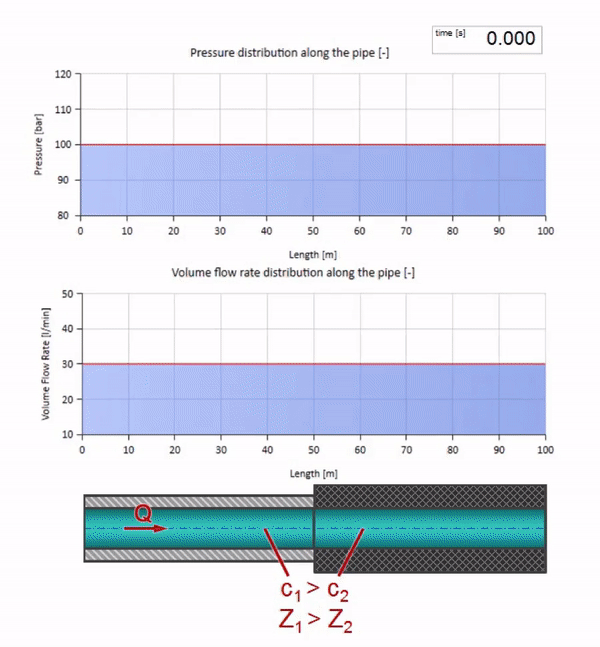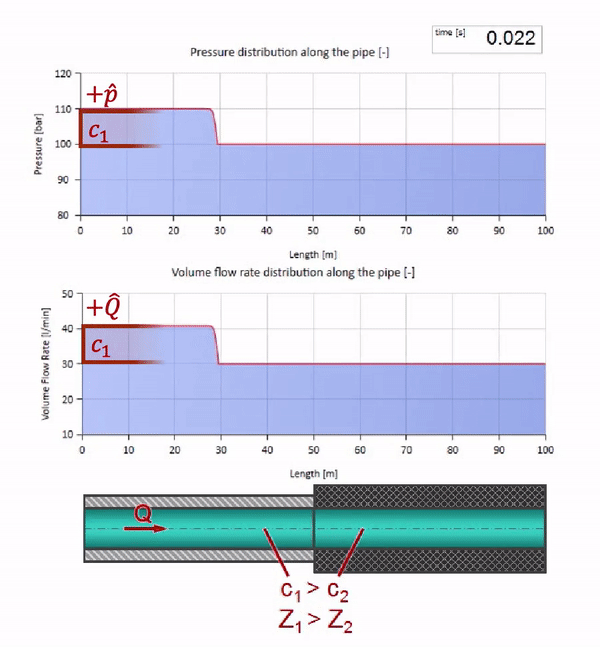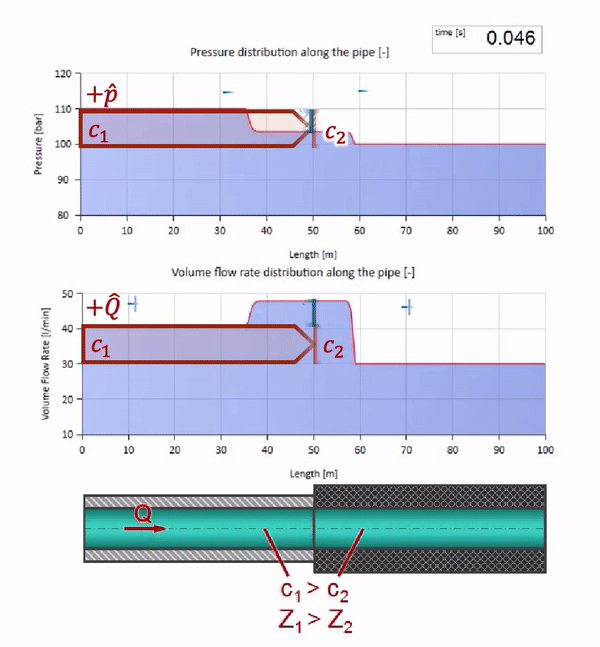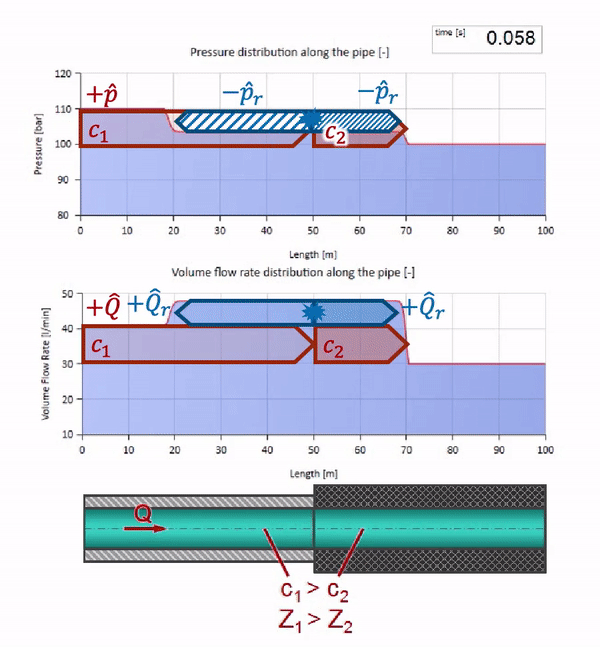
波のインピーダンスの値がゼロで無限に大きい極端な場合を考えるといいでしょう。 これは、それぞれ一定の圧力と閉じた端を持つタンクへのパイプラインの出口になります。 コメントなしでこれらのアニメーションを残します。


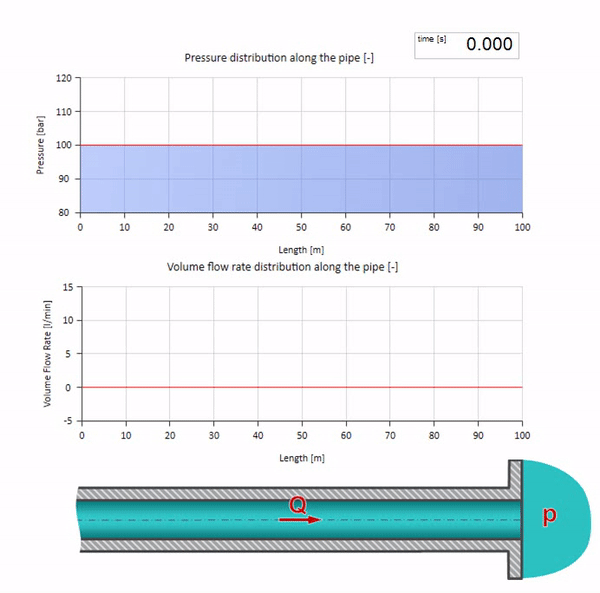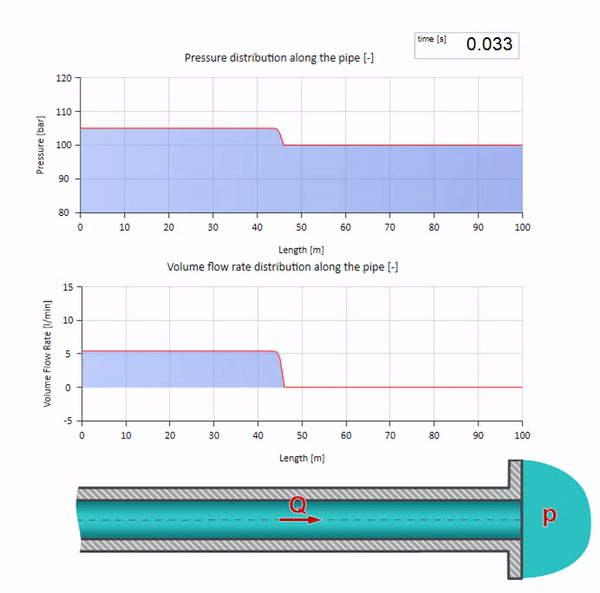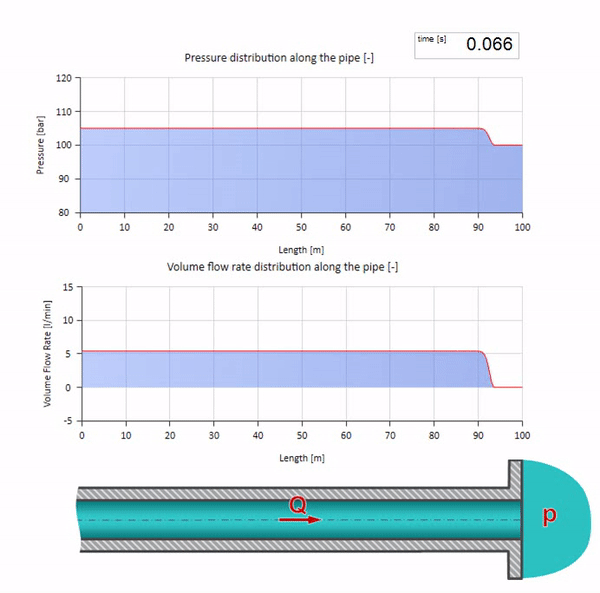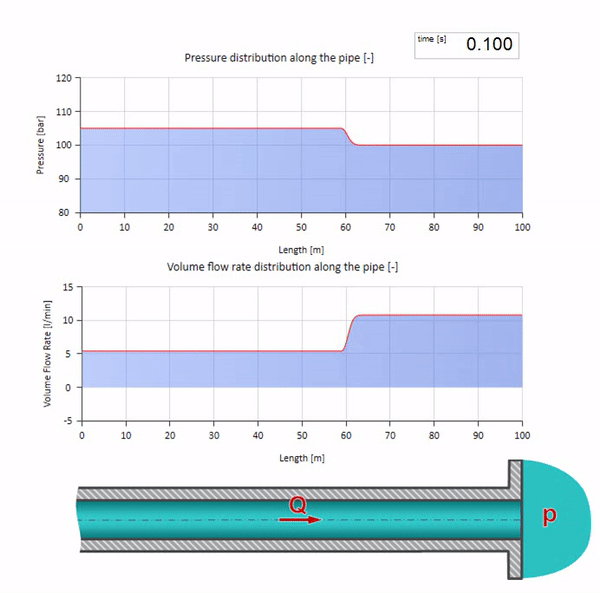
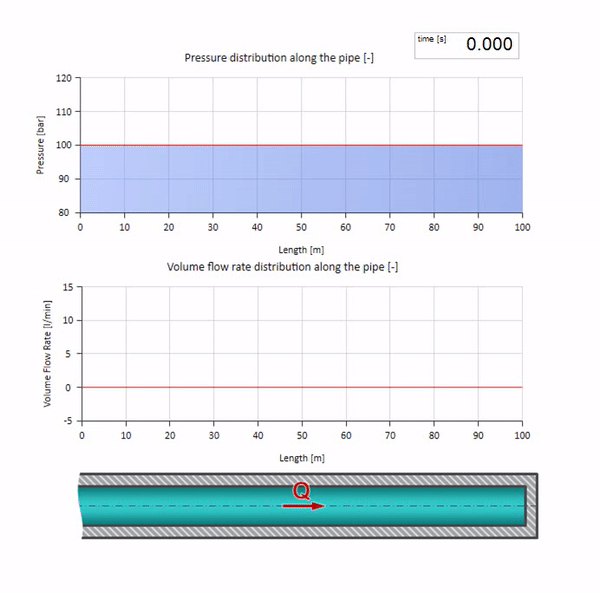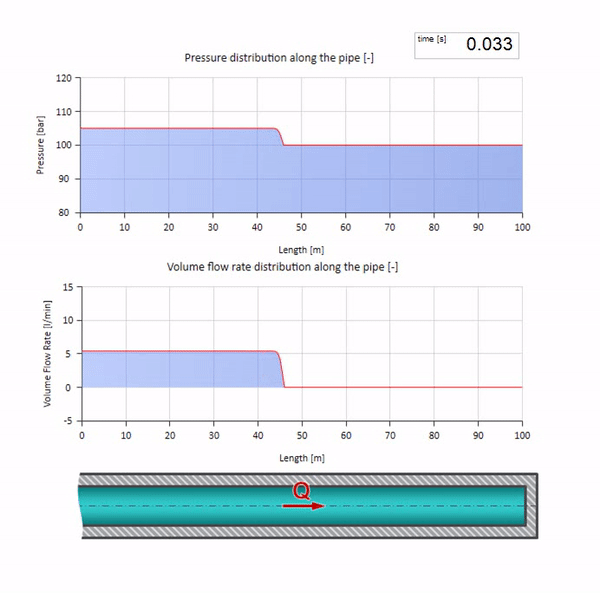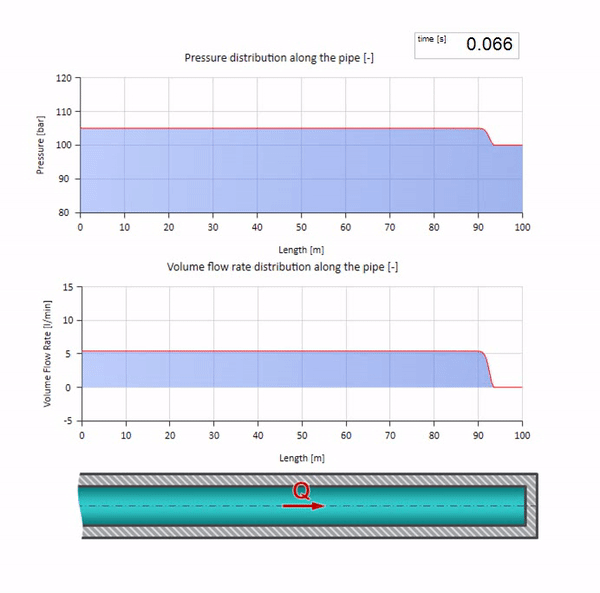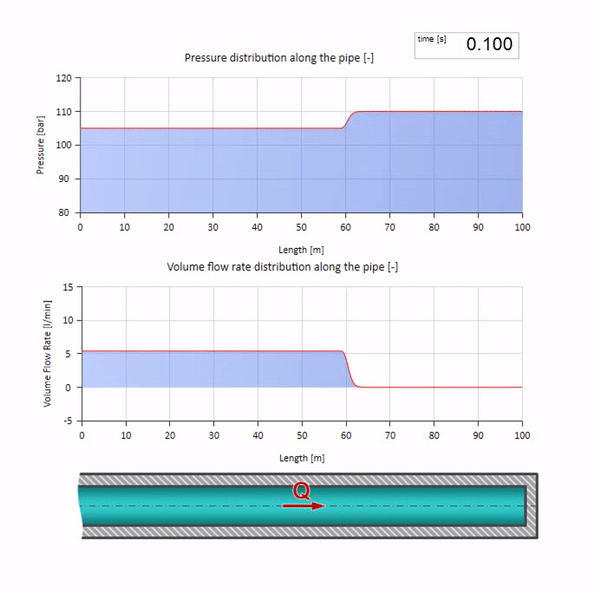
これら2つのケースを組み合わせると、古典的な油圧ショックが発生します。

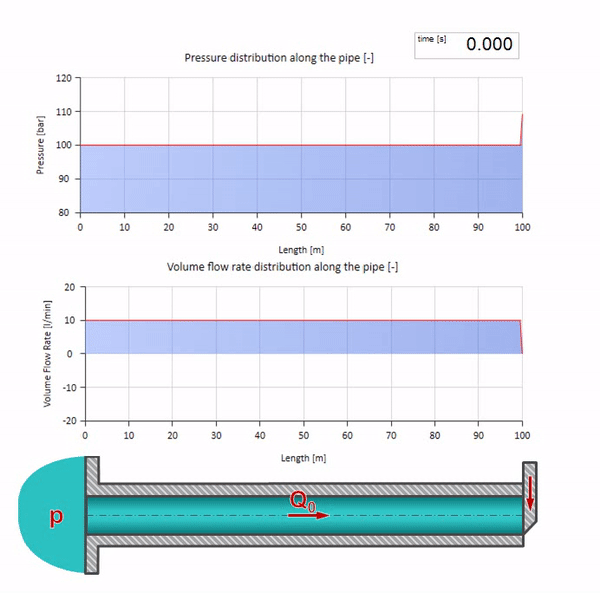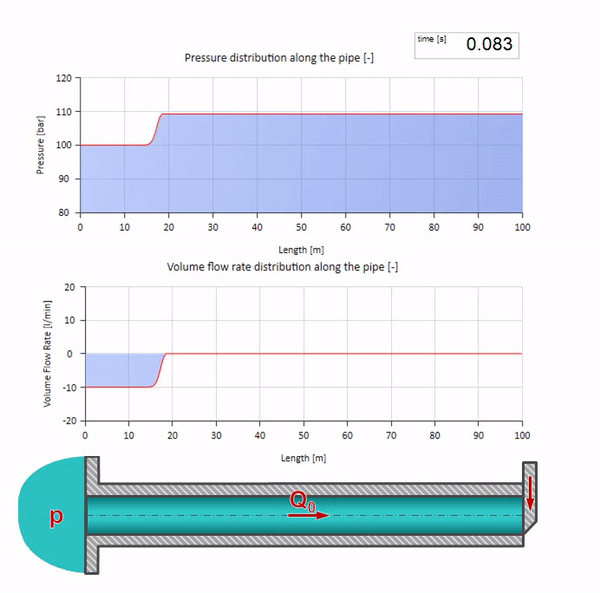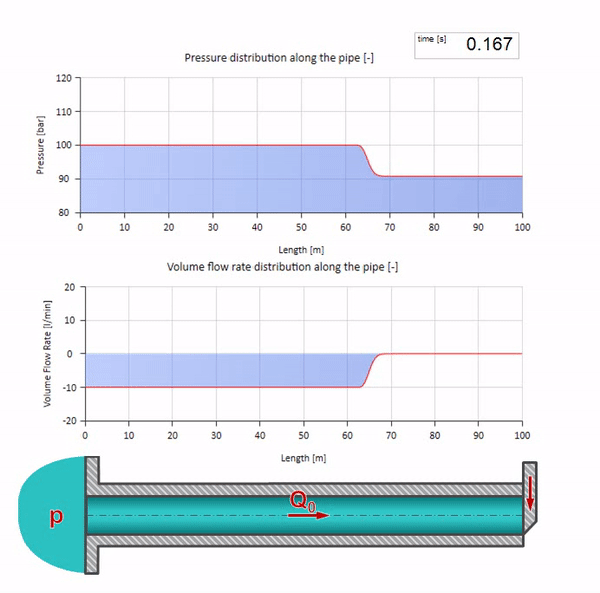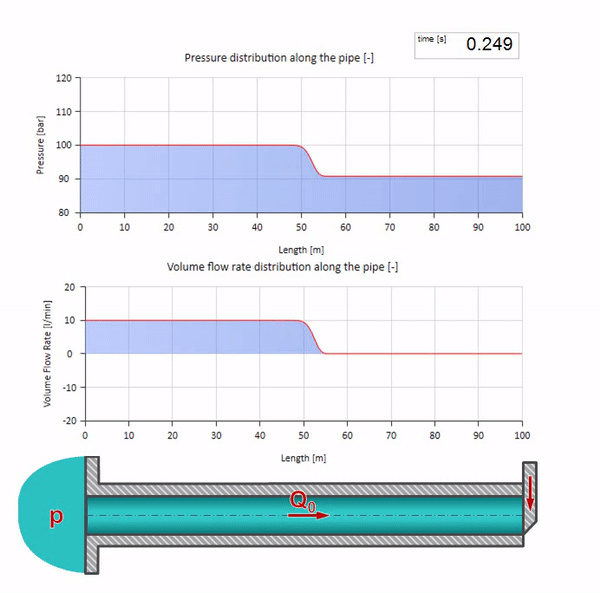
ここで、最初の瞬間には、ある種の流量があります。これは、パイプの右端で即座にゼロになります（バルブが閉じます）。 下降流と上昇圧力の波が左に動き始めます。 これらの波は、インピーダンスがゼロのパイプラインの右端から反射されます。 摩擦がなければ、このプロセスは無限になります。
興味深いことに、上記の式を使用して、水撃のジューコフスキー方程式を導出できます。

$$

$$\ widehat p = Z_L \ widehat Q \;$$

所定の値からゼロまで低下すると仮定して、速度を通る流量を表し、波動インピーダンスをペイントします。

$$

$$\ widehat p = A \; v_0 \; \ frac {\ rho \; c} {\ A} = \ rho \; c \; v_0$$

シャッターが瞬時に閉じられたときに発生する圧力ジャンプの値を取得します。

注釈

1. アーヘンのライン・ヴェストファーレン工科大学の油圧工学科で、油圧に関する基本的な教科書の長から記事を書くように促されました。私の意見では、油圧ラインのプロセスが最も明確に説明されています-1223-1）。
2. SimulationXプログラムでアニメーションが作成され、特性の方法を使用して計算が実行されました