長時間信号をセグメントに分割するタスクがいくつかあり、各セグメントは個別に処理されます。 特に、このアプローチは、合成でウィンドウフーリエ変換を使用して信号を分析するために使用されます。 ノイズ除去、テンポ変更、非線形フィルタリング、オーディオデータ圧縮などのスペクトル処理においても同様です。

パーティショニング自体のプロセスは、オフセット付きの重み（ window ）関数の乗算によって数学的に表されます 。 最も単純なウィンドウ（長方形）の場合、次のようになります。

ソース信号：



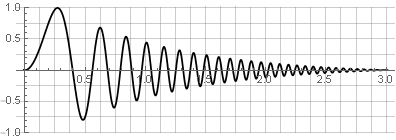
パーティション：







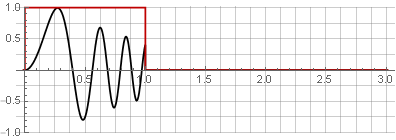
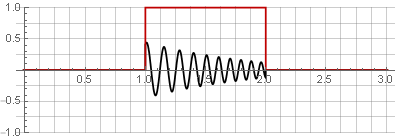
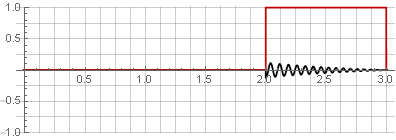
元の信号を単純に加算することで復元できます。

詳細

しかし いくつかの理由から、長方形関数は最適なウィンドウ関数ではありません。 スペクトル分析では、（通常は高速な）離散フーリエ変換により、分析されたデータブロックは「ループ」しているように見え、エッジのギャップとスペクトルの歪みにつながります。



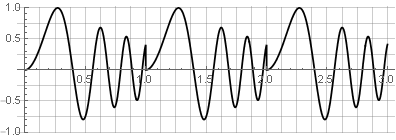
また、逆合成には適していません-変更を加えるとブレークが発生するためです-たとえば、いずれかのパーツを逆にしようとすると：



これらの欠点を排除するために、オーバーラップが使用されます-後続の各ウィンドウが前のウィンドウからデータの一部をキャプチャするとき そして、それに応じて、重みウィンドウは徐々に端まで下がります。

50％のオーバーラップ

ほとんどの場合、50％のオーバーラップでハンナウィンドウ （「レイズドコサイン」とも呼ばれます）を使用します 。








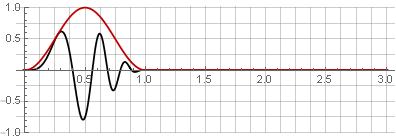
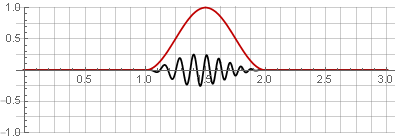
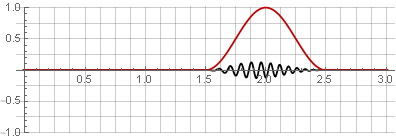
加算中のコサイン関数の対称性により、それらは1に合計されます。



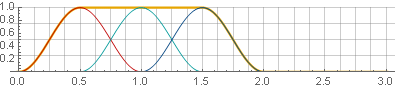
さて、逆合成では、ギャップは得られませんが、ウィンドウの境界で値がまだゼロになるという条件でのみです。 たとえば、パーツの1つを反転する場合、滑らかさは侵害されません。

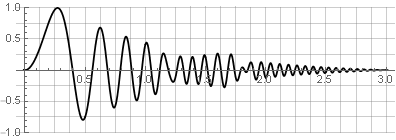
ダブルオーバーレイ処理

高速フーリエ変換（FFT）を使用した信号処理のアルゴリズムをさらに詳しく見てみましょう。

1. ウィンドウオーバーレイを使用して信号をセグメントに分割します。
2. 直接FFT;
3. スペクトル処理;
4. 逆FFT;
5. 繰り返されたウィンドウオーバーレイ（逆FFTの後、境界線が壊れずにゼロにドッキングされるとは限らないため）;
6. 結果のセグメントの合計。

この場合、スペクトル処理が実行されない場合、出力信号は入力信号と同一である必要があります（不可避の時間遅延のみ）。

Hannウィンドウを使用する場合、50％のオーバーラップは、ディップが発生するため、もはや十分ではありません。



二重の重なりは二乗に等しいので、明らかな解決策はHannウィンドウのルートを使用して二乗を補正することです。



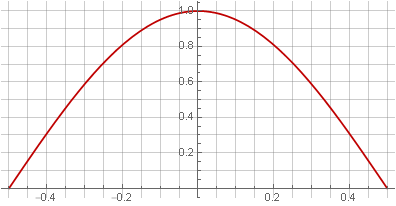
ただし、この場合、ウィンドウはエッジで滑らかでなくなりました-一次導関数にギャップが現れました。


あなたは他の方法で行くことができます-75％のオーバーラップを使用すると、ウィンドウも定数に合計されます- $$$1$、そして $$$\ frac {3} {2}$：



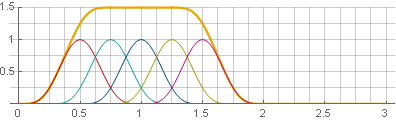
この場合、私たちは幸運でした。 正方形を合計に拡張すると、2つのハンナウィンドウの構成であるが、スケールが異なるため、必要な要件を満たすことができることがわかります。

$$

$$\左（\ frac {\ cos（2 \ pi x）+1} {2} \ right）^ 2 = \ frac {\ cos（2 \ pi x）+1} {2} + \ frac {\ cos （4 \ pi x）-1} {8}$$

他のウィンドウ関数では、このようなフォーカスは機能しません。 また、すべての標準ウィンドウ関数が、50％のオーバーラップでも定数で合計を提供できるわけではありません。

アイデア

Hannウィンドウは独立した関数としてではなく、2つの区分的連続関数（それらの詳細な説明については別の記事で説明されています）の差として考慮できます。 たとえば、次の関数を使用します

$$

$$\ left \ {\ begin {array} {ll} -1＆x \ leqslant -1 \\ 1＆x \ geqslant 1 \\ \ sin \ left（\ frac {\ pi x} {2} \ right）＆ -1 <x <1 \\ \ end {array} \ right。$$

書ける

$$

$$f（x + 1）-f（x-1）$$

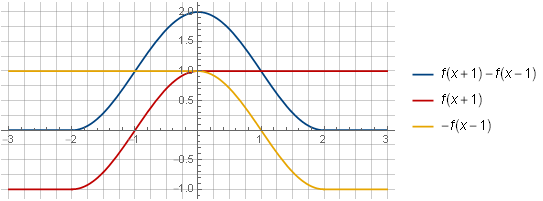
このような2つのウィンドウの合計のコンポーネントを検討すると、定数にまとめる機能がより視覚的になります。



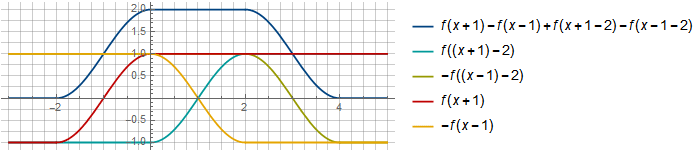
セグメント上 $$$[0.2]$機能に加えて相互補償を受けました $$$-f（x-1）$そして $$$f（（x + 1）-2）$以来 $$$f（（x + 1）-2）= f（x-1）$

次の例のように、オーバーラップが多い別のオフセットを選択できます。

$$

$$f \左（x + \ frac {1} {2} \右）-f \左（x- \ frac {1} {2} \右）$$

そして、ステップでシフトするとき $$$\ frac {1} {2}$、それらは定数に合計されます：



ウィンドウ関数のコンポーネントを再配置すると、同じハンウィンドウが表示されることがわかります。

したがって、さまざまな制限機能を使用して、必要な形状のウィンドウを形成できます。

最終式

定義領域と値がオーバーラップの量に依存しないように、スケールを設定するだけです。 間隔でウィンドウを定義する $$$[0,1]$私たちは得る

$$

$$\ frac {f \ left（\ frac {2 tx} {t-1} -1 \ right）-f \ left（\ frac {2 t（x-1）} {t-1} +1 \ right） } {2}$$

どこで $$$f$-形式の区分的連続関数

$$

$$\ left \ {\ begin {array} {ll} -1＆x \ leqslant -1 \\ 1＆x \ geqslant 1 \\ g（x）＆-1 <x <1 \\ \ end {array} \右$$

でも $$$g$-ポイント間のいくつかの補間関数 $$$（-1、-1）$そして $$$（1,1）$。

パラメータ $$$t$オーバーラップのレベルを決定します-次の各ウィンドウをシフトする必要があるステップを決定するディバイダー、 $$$x_ {n + 1} = x_n + \ frac {1} {t}$、1より大きくなければなりません。 $$$t> 1$。

重複率 $$$p$式によって計算できます

$$

$$p = \ frac {100（t-1）} {t}$$

そしてその逆

$$

$$t = \ frac {100} {100-p}$$

ウィンドウの最終的なビューは、オーバーラップのレベルの選択と制限機能の選択の両方に依存します。

いくつかの興味深い例

ここでは、すべてが開始されたいくつかの既製のソリューションを検討します。 簡単にするために、単純な補間関数を考えます $$$g（x）$、他のストラップなし。

多項式ウィンドウ

それらは計算上最も安価です。 以前に派生した式を使用する

$$

$$\ frac {2 x \ガンマ\左（n + \ frac {1} {2} \右）\、_ 2F_1 \左（\ frac {1} {2}、1-n; \ frac {3} {2} ; x ^ 2 \ right）} {\ sqrt {\ pi} \ Gamma（n）}$$

エッジでのウィンドウの必要な滑らかさを提供する高導関数で与えられた数のゼロで多項式を取得します。


nの値が異なるウィンドウの75％のオーバーラップにより、ウィンドウは次のようになります。



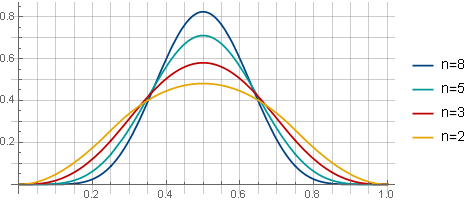
そして、ルート抽出の場合-このように（75％オーバーラップを使用する場合）：



または（50％のオーバーラップを使用する場合）：

最も滑らかなウィンドウ

機能

$$

$$\ tanh \ left（\ frac {k x} {\ sqrt {1-x ^ 2}} \ right）$$

無限に微分可能であり、エッジでのすべての導関数が0（微分規則に基づいて導関数を検討することで証明できます-各項にゼロ化係数があります）。 これにより、その基礎に基づいてウィンドウを構築できます。その派生物にはすべてギャップがありません。

ウィンドウビュー「スカート」

このタイプのウィンドウの必要性は、FFTの解像度を上げることによって引き起こされますが、中心での集中度を高めることにより、高周波での「時間周波数不確実性」効果の影響を減らします。

まず、目的のウィンドウ関数のタイプを決定します-たとえば、次のように：

$$

$$-\ log \ left（k ^ 2 x ^ 2 + 1 \ right）+ \ log \ left（k ^ 2 + 1 \ right）-\ frac {k ^ 2 \ left（1-x ^ 2 \ right） } {k ^ 2 + 1}$$

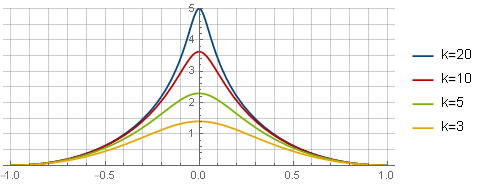
ここで、最初の項は関数自体の形式を決定し、2番目は横軸との交点を提供し、3番目（放物線）は滑らかな結合のためにエッジで導関数をリセットします。 およびパラメーター $$$k$ピークの「シャープネス」を定義します。 この形式では、まだ使用に適していません-最初に、統合とスケーリングによって制限関数を取得する必要があります。

$$

$$\ frac {kx \ left（k ^ 2 \ left（x ^ 2 + 3 \ right）+6 \ right）+3 \ left（k ^ 2 + 1 \ right）\ left（kx \ left（\ log \左（k ^ 2 + 1 \右）-\ log \左（k ^ 2 x ^ 2 + 1 \右）\右）-2 \ tan ^ {-1}（kx）\右）} {4 k ^ 3-6 \左（k ^ 2 + 1 \右）\ tan ^ {-1}（k）+6 k}$$

便宜上、パラメーターをバインドできます $$$k$オーバーラップのレベルまで $$$t$-たとえば、ウィンドウの中央の4次導関数が0になるようにします。 $$$k$と見なされます $$$\ sqrt {3}（t-1）$：



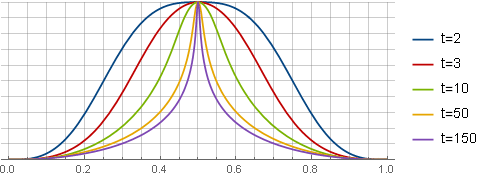
ここでは、わかりやすくするために、すべてのウィンドウを同じスケールに縮小しています。

ニードルビューウィンドウ

これは、前のウィンドウのより「攻撃的な」バージョンです。 双曲線が基礎として選択され、そこから連続的な変換を通して

$$

$$\ frac {1} {x} \ to \ frac {1} {\ sqrt {x ^ 2}} \ to \ frac {1} {\ sqrt {x ^ 2 + 1}} \ to \ frac {1} {\ sqrt {k ^ 2 x ^ 2 + 1}} \ to \ frac {\ left（1-x ^ 2 \ right）^ 2} {\ sqrt {k ^ 2 x ^ 2 + 1}}$$

統合とスケーリングの形で同じ手順を使用して式を得た

$$

$$\ frac {kx \ left（2 k ^ 2 \ left（x ^ 2-4 \ right）-3 \ right）\ sqrt {k ^ 2 x ^ 2 + 1} + \ left（8 \ left（k ^ 4 + k ^ 2 \右）+3 \右）\ sinh ^ {-1}（kx）} {\ left（8 \左（k ^ 4 + k ^ 2 \右）+3 \右）\ sinh ^ {-1}（k）-3 k \ sqrt {k ^ 2 + 1} \左（2 k ^ 2 + 1 \右）}$$

ここで、パラメータをバインドすることもできます $$$k$オーバーラップのレベルまで。 4次導関数の方程式の直接的な解は面倒な結果を与えるため、次のように定義することにより、画像内の前のウィンドウと類似性の画像を作成するだけです。 $$$k$どうやって $$$k（t-1）$したがって、パラメータの役割を保証します $$$k$「微調整」として。 で $$$k = 2.22$ウィンドウは次のようになります。

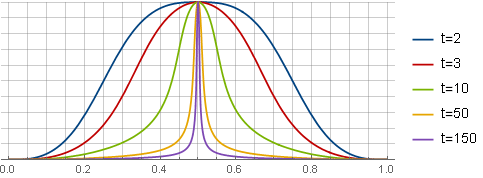
非対称ウィンドウ

ウィンドウ関数はまったく対称である必要はありません。 鋭いアタックと滑らかな減衰を持つウィンドウが必要だとしましょう。 すでによく知られているスキームに従って取得できます。まず関数の目的の形式を決定し、次に統合により制限関数を取得します。 ここでは、非対称のために中心が原点を通過しなくなるため、タスクが少し複雑になります。そのため、追加の計算ステップが追加されます。 これはまた、結果として式がかなり面倒であるという事実につながります。 たとえば、最も単純なオプション-多項式の重みウィンドウを乗算した放物線を考えてみましょう。

$$

$$（1-x）^ 2 \左（1-x ^ {10} \右）^ 2$$

ここでは、重み付きウィンドウ内のxの次数（つまり10）が攻撃の「シャープネス」を決定します。 シンボリックパラメーターではなく特定の値を使用して、わかりやすくするために数式を簡略化しました。必要に応じて、後で再計算できます。

統合後、単にスケーリングするだけでは不十分です-エッジを揃える必要があります：



これを行うには、まず関数を上にシフトして左端を揃え、次に右端の2にスケーリングして1を減算します。 次に、次の式を取得します。

$$

$$\ frac {8775 \左（\ frac {x ^ {27}} {27}-\ frac {2 x ^ {26}} {26} + \ frac {x ^ {25}} {25}-\ frac {2 x ^ {15}} {15} + \ frac {4 x ^ {14}} {14}-\ frac {2 x ^ {13}} {13} + \ frac {x ^ 3} {3} -x ^ 2 + x + \ frac {117592} {61425} \右）} {9856} -1$$

最終的なウィンドウが希望の外観になるためには、十分に大きなレベルのオーバーラップを提供する必要もあります。

おわりに

同様の方法で、他のベル型の関数（ガウス関数など）からウィンドウを構築できます。 また、既に考慮されているものを変更して、より滑らかにしたり、曲線の形状を変更したりすることもできます。

考慮外に、そのような窓関数のスペクトル構成は残りました-別の研究がこれに専念されるべきです。

Wolfram Mathematica文書の形式の記事のもう少し高度なバージョン（検討中のウィンドウのパラメーターを動的に変更する機能と非表示の式）はこちらからダウンロードできます 。