チックタックトー「国境なき」

三目並べ...誰もがそれらを演奏した、と確信しています。 このゲームはシンプルで魅力的です。特に、レッスンのどこかでカップルをドラッグすると、ノートブックシートとシンプルな鉛筆以外は手元にありません。 かつて9マスに十字や円を描くことを最初に推測したのは誰なのかわかりませんが、それ以来、特に人々がそのバリ​​エーションの多くを考え出して以来、ゲームは需要を失いませんでした。



この記事では、チックタックトーのこれらのバリエーションの1つを再生するためにJavaScriptでAIを開発するプロセスについて説明します。かなり多くの資料を入手しましたが、アニメーションと写真で希釈しました。 いずれにしても、少なくとも試してみる価値はあります。
このバージョンのゲームとオリジナルの違いは次のとおりです。

1. フィールドは任意に大きくすることができます（ノートブックの長さ）
2. 勝者は、 5ピース （あなたがそれらを呼び出すことができる場合）を連続して置くものです。

すべてがシンプルであると同時に複雑です。古典的なアナログのように、ゲームの結果を事前に計算することはできません。 この「小さな投影」は多くの時間と神経を奪いました。 おもしろいと思います。

始める前に

記事のボリュームについては事前に謝罪せざるを得ず、一部の場所ではまったくわかりにくい意見を述べましたが、コンテンツと品質を損なうことなく群れを絞ることはできませんでした。
最初に結果に慣れることをお勧めします。 コード

キーボードショートカットとコマンド：

• D -AIはあなたのために動きます
• T-セル重量を参照
• コンソールで、 SHOW_WEIGHTS = trueと記述して 、分析されたすべてのセルの重みを表示します。

始めましょう

ゲーム自体の実装から始める必要があります。つまり、 これまでのところ、ボットなしで2人のプレーヤー用のアプリケーションを作成します。 私の目的では、javascript + jquery + bootstrap4を使用することにしましたが、実際には使用されていませんが、そのままにしておく方が良いでしょう。そうしないと、テーブルが浮いてしまいます。 伝えるべき特別なものはありません。js、jquery、およびbootstrapには多くの資料があります。 MVCを使用したとしか言えません。 とにかく、私は絶対にすべてのコードを説明しません-それなしで多くの材料がありました。

それで、競技場の準備ができました。 セルに形状を設定できます。 しかし、どのプレイヤーの勝利も決して決まっていませんでした。

ゲームスキャンの終了

プレイヤーの1人が5個を連続して置くと、ゲームは終了します。 「簡単です！」と思いました。 そして、彼はフィールドのすべてのセルを完全にスキャンし始めました。最初はすべて水平、次に垂直、そして最後に対角線です。

これは馬鹿げた方法ですが、うまくいきました。 しかし、それは大幅に改善される可能性があり、私はそれを行いました。ほとんどのセルはゲーム中は空のままです-競技場が大きすぎて完全に埋めることができません。 すべての動きをスキャンする必要があり、1つの動きに1つのピースのみが配置されているため、このピース（セル）のみに焦点を合わせることができます：同じセルを所有するセルの水平、垂直および2つの対角線のみをスキャンします

さらに、すべての細胞株をスキャンする必要はありません。 ゲームの終了は連続して5個であるため、互いに6セル離れているピースは興味がありません。 両側の5つのセルをスキャンすれば十分です。 分かりませんか？ 以下のアニメーションをご覧ください。

ボット自体に取りかかりましょう

そのため、すでにtic-tac-toeを使用してページを作成しました。 メインタスク-AIに渡します。
方法がわからない場合は、コードを取得して作成することはできません。ボットのロジックを考える必要があります。

一番下の行は、競技場、少なくともその一部を分析し、フィールド上の各セルの価格（重量）を計算することです。 最も重みのあるセル-最も有望な-ボットはそこに数字を置きます。 主な問題は、1つのセルの重みを計算することです。

用語

十字とつま先は数字です。
攻撃は、同じ線上に並んで立っている複数の同一人物と呼ばれます。 実際、これはたくさんあります。 攻撃のピースの数はその力です。 1つの独立した部分も攻撃です（パワー1）。

隣接する攻撃セル（端）には、空のセルまたは敵の駒が存在する場合があります。 「端」に2つの空のセルがある攻撃は2つの方向に展開できると考えるのが論理的であり、より有望です。 攻撃の「端」にある空のセルの数は、そのポテンシャルと呼ばれます。 電位は0、1、2のいずれかです。
攻撃を次のように表します： [攻撃力、潜在力] 。 たとえば、 攻撃[4：1] 。


図1.攻撃[4：1]

分析の過程で、特定の領域に入るすべてのセルを評価します。 各セルはその重みを計算します 。 このセルが影響するすべての攻撃の重みに基づいて計算されます。

分析の本質

競技場では、すでに1人目と2人目のプレーヤーが何度か攻撃されていると想像してください。 プレーヤーの1人が移動します（クロスを許可します）。 当然、彼は空のセルに移動します。

1. 攻撃を開発し、複数の攻撃を開発して、その力を高めてください。 新しい攻撃を開始するなど。
2. 敵の攻撃の発生を防ぐか、完全にブロックします。

つまり、主人公は攻撃と防御ができます。 または、一度にすべてを一度に実行できます。 彼にとって、最初と2番目の両方が重要です。

分析の本質は次のとおりです。

1. ボットは、チェックされたセル内の数字を置換します。最初は十字、次にゼロです。
2. 次に、彼はそのような動きによって受信されたすべての攻撃を検索し、それらの重みを要約します。
3. 受け取った量はセルの重量です。
4. 同様のアルゴリズムが競技場のすべてのセルに対して実行されます。

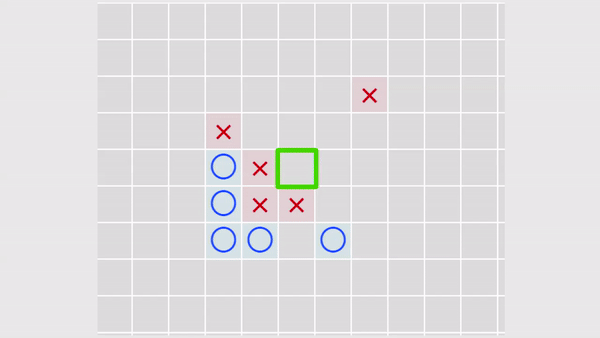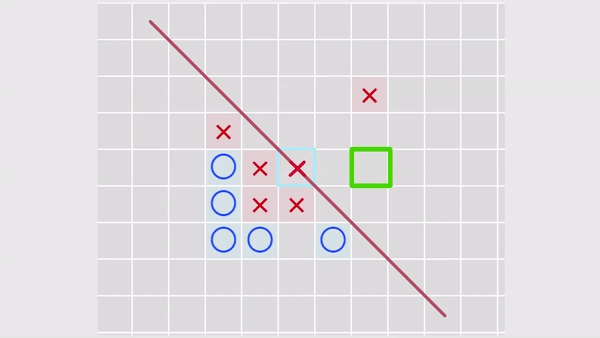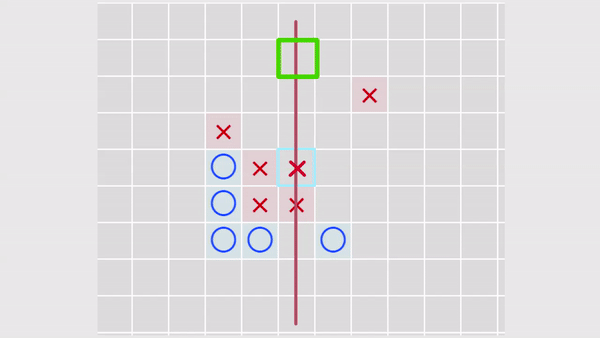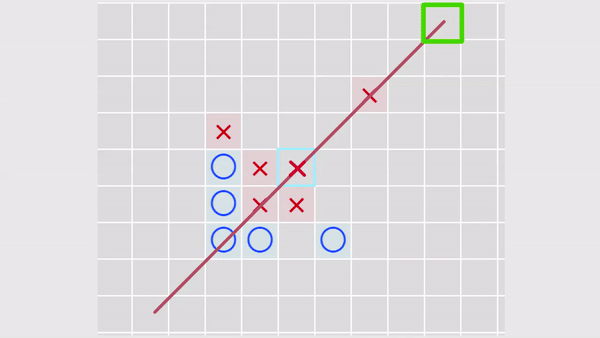
実際、このようなアルゴリズムを使用して、このように進むとどうなるかを確認します...そして、相手がそのように進むとどうなるかを確認します。 1つのステップを楽しみにして、最も適切なセルを選択します-最も高い重みを持ちます。

セルの重みが他のセルよりも大きい場合、それはより危険な攻撃の作成につながるか、強力な敵の攻撃をブロックします。 すべてが論理的です...それは私には思えます。
ページに移動してコンソールにSHOW_WEIGHTS = trueと記述すると、アルゴリズムの動作を視覚的に感じることができます（セルの重みが表示されます）。

攻撃の重み

私は自分の頭を駆使して、攻撃と重みのこのような対応をもたらしました。

 ATTACK_WEIGHT = [[],[],[],[],[],[]]; ATTACK_WEIGHT[1][1] = 0.1; ATTACK_WEIGHT[2][1] = 2; ATTACK_WEIGHT[3][1] = 4; ATTACK_WEIGHT[4][1] = 6; ATTACK_WEIGHT[5][1] = 200; ATTACK_WEIGHT[1][2] = 0.25; ATTACK_WEIGHT[2][2] = 5; ATTACK_WEIGHT[3][2] = 7; ATTACK_WEIGHT[4][2] = 100; ATTACK_WEIGHT[5][2] = 200; ATTACK_WEIGHT[5][0] = 200; 

経験的に選択-これはおそらく最良の選択肢ではありません。

アレイに非常に大きな重みで5の攻撃力を追加しました。 これは、ボットがゲームを分析し、一歩前進を見ているという事実によって説明できます（セル内の数字を置き換えます）。 そのような攻撃をスキップすることは、敗北に他なりません。 まあ、または勝利...誰に応じて。

高い可能性のある攻撃はより高く評価されます。

ほとんどの場合、攻撃[4：2]がゲームの結果を決定します。 プレイヤーがそのような攻撃を作成できた場合、対戦相手はそれをブロックできなくなります。 しかし、これは勝利ではありません。 フィールドに攻撃[4：2]がある場合でも、敵はゲームをより速く終了できるため、その重みは5のべき乗の攻撃よりも小さくなります。下の例を参照してください。


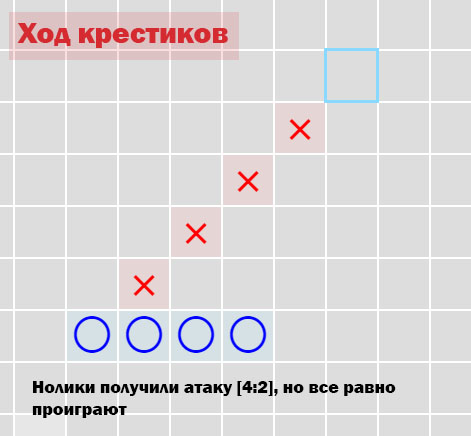図2.攻撃[4：2]

引き裂かれた攻撃

この段落ではコードは示されていません。 ここでは、攻撃ディバイダーの概念を紹介し、 「破壊攻撃」の本質を説明します。

次の状況を考慮してください。5個以下の複数の空のセルを削除するためにFigureを置き換える場合、もう1つが配置されます。

そして、同じ行にある2つの同一の数字...視覚的には攻撃のように見えますが、実際にはそうではありません。 このような「破壊された」攻撃も潜在的な脅威になるため、順序ではありません。

特にそのような場合、攻撃ごとに除数を計算します。 初期値は1です。

1. 私たちは、いくつかの普通の「破壊された」攻撃を提示します
2. 中央の攻撃と側面の間の空のセルの数を数えます
3. 空のセルごとに、除数が1ずつ増加します
4. 通常通り中央攻撃の重み、サイド攻撃の重みを計算します-除数で除算します

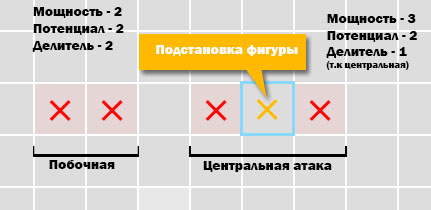図3.「引き裂かれた攻撃」の分析。 黄色の十字が付いたセルがスキャンされます。

したがって、引き裂かれた攻撃もAIによって考慮されます。 実際、これらは通常の攻撃ですが、スキャンされたセルから遠ざかるほど影響が小さくなり、それに応じて重みが小さくなります（仕切りのおかげ）。

攻撃検索アルゴリズム

最初に、攻撃クラスを作成します。 攻撃には3つの属性がありますが、これについては前に説明しました。

 class Attack{ constructor( cap = 0, pot = 0, div = 1 ){ this.capability = cap; // this.potential = pot; // this.divider = div; // } 

そして、特定の攻撃の重みを返す1つのメソッド ：

 countWeigth(){ return ATTACK_WEIGHT[ this.capability, this.potential ] / this.divider } } 

次。 1つのセルに対するすべての攻撃の検索を次のように分割します。

1. 水平検索
2. 垂直検索
3. 45度の対角検索
4. 135度の斜め検索

これらはすべて行であり、これらの行に対する攻撃を検索するアルゴリズムは一般化できます： checkLineクラス 。

ただし、行全体をチェックする必要はありません。 興味のある最大の攻撃力は5です。もちろん、たとえば6の力で攻撃を作成することは可能です。 しかし、次の動きのゲーム状況を分析するAIの場合、6または5と同じです。これらの攻撃のいずれかを取得する見込みは、次の動きのゲームの終了を示します。 したがって、分析されたセルの重量は両方のケースで同じになります。

クラス属性：

 class checkLine{ constructor(){ //,        this.subFig = "×"; //     .    «0» - . this.Attacks = []; //  this.curAttack = new Attack; // (      ) this.iter = 1; //,     this.checkEdge = false; 

問題が発生する可能性があるため、ここで停止する必要があります。最大攻撃力が5の場合、6番目のセルをチェックする理由です。

例は次のとおりです。画像内の1のべき乗の攻撃は、スキャンされた領域の境界にあります。 この攻撃の可能性を知るには、「海外を見る」必要があります。


図 3. 6番目のセルをスキャンします。 6番目のセルをスキャンしないと、攻撃の可能性を誤って判断できます。

  //   this.attackplace = 1; } 

いくつかの攻撃を完了するのに十分なスペースがない可能性があります。 攻撃場所をカウントすると、どの攻撃が見込みがないかを事前に理解できます。


図 4.攻撃する場所

アルゴリズムは次のとおりです。

1）中央のセルから始めましょう。 空にする必要があります（その中に移動しますか？しかし、AIが次の移動の分析のためにこのセルの数値を置換する必要があることを忘れないでください。置換する数値はthis.subfigです -デフォルトはクロスです。中央のセルは置換後に最初に何らかの形状を含むため、 this.curAttack攻撃のいくつかの種類に属します。

• その電力は1以上になります（中央のセルの数字）
• 分周器-1 私たちは集中攻撃について話している（それはスキャンされたセルに属する）;
• ポテンシャルはまだわかっていません-デフォルトは0です。

これらすべてのポイントをデフォルトのコンストラクタ値に表示しました-上記のコードを参照してください。

2）次に、反復子を減らして、スキャンしたセルの片側の5つのセルを整理します。 getAttacks関数（cellX、cellY、subFig、dx、dy）がこれを担当します。ここで、

cellX、cellY-チェックされたセルの座標
subFig-チェックされたセルで置換する図
dx、dy-サイクルのx座標とy座標の変化-これが探索方向の設定方法です：

• 水平（dx = 1、dy = 0）
• 垂直（dx = 0、dy = 1）
• 対角線45（dx = 1、dy = -1）
• 対角線135（dx = 1、dy = 1）

ある意味では、これは検索ラインに平行なベクトルです。 したがって、1つの関数で4方向の検索が可能になり、DRY原則に再度違反することはありません。

機能コード：

 getAttacks( cellX, cellY, subFig, dx, dy ){ this.substitudeFigure( subFig ); //  –  ... for( var x = cellX - dx, y = cellY - dy; Math.abs( x - cellX ) <= 5 && Math.abs( y - cellY ) <= 5; x -= dx, y -= dy ) if( this.checkCell( x, y ) ) break; //: //    (  ) this.turnAround(); //  -    ... for( var x = cellX + dx, y = cellY + dy; Math.abs( x - cellX ) <= 5 && Math.abs( y - cellY ) <= 5; x += dx, y += dy ) if( this.checkCell( x, y ) ) break; return this.Attacks; } 

checkCell（）が何かを返すと、ループが停止することに注意してください。

3）これらのセルの数値を確認します。
checkCell（x、y）関数がこれを担当します。

まず、形状をfig変数に書き込みます。
Model.Fieldは私たちの競技場です。

 checkCell( x, y ){ var fig = Model.Field[x] && Model.Field[x][y] !== undefined ? Model.Field[x][y] : 'b'; 

figは、「x」、「o」、「b」（境界線）、0（空のセル）です。

• そのような数値が中央セルの数値（ this.subFig ）と一致する場合、アルゴリズムを続行します。その後、攻撃をスキャンし続け、すべてが正常であり、同じ精神で続行します。 攻撃の余分な部分は、その力（ this.curAttack.capability ）と場所（ this.attackplace ）のプラスです。
  
  （次の段落のコードを参照）
• これが別の数字である場合、前にスキャンした攻撃（this.curAttack）はこちら側からブロックされます。 攻撃パラメーターは何も変更せず、攻撃の配列に書き込み、ループから抜け出します。
  
  

   if( fig == '○' || fig == '×' ){ if( this.subFig != fig ){ //  this.Attacks.push( this.curAttack ); //  return fig; //      } else{ //    this.curAttack.capability++; // +   this.attackplace++; // +   } } 

  
  
• そのようなセルが存在しない場合、フィールド境界から落ちたことを意味し、攻撃がブロックされることを意味します。 すべての攻撃の配列に書き込み、ループを終了します。
  
  

   else if( fig == 'b' ){ // this.Attacks.push( this.curAttack ); return 'b'; } 

  
  
• 空のケージをキャッチした場合、それは現在の攻撃が終了したことを意味します。 さらに、攻撃の可能性と場所（攻撃がブロックされていないため）。 ただし、ループを終了することはありません-これは「破壊攻撃」である可能性があります-this.curAttackをthis.Attacks []行のすべての攻撃の配列に書き込むだけです。 新しい「現在の」攻撃を作成し、その除数を1増やします（これはサイド攻撃です）。
  
  

   else{ //  if( this.curAttack.capability ){ this.curAttack.potential++; this.Attacks.push( this.curAttack ); this.curAttack = new Attack; this.curAttack.potential++; } this.curAttack.divider++; this.attackplace++; } 

  
  

4）5番目のセルで図が中央のセルと一致する場合、攻撃は境界に対して「 停止 」し、攻撃の可能性を判断するには、「境界をチェック」する必要があります（ this.checkEdge = true ）。

 if( this.iter == 4 && fig == this.subFig ) // 5-  this.checkEdge = true; else if( this.iter == 5 ){ if( this.checkEdge ){ if( fig == this.curFig || fig == 0 ) this.curAttack.potential++; this.Attacks.push( this.curAttack ) } return 0; } this.iter++ 

checkCell関数の準備ができました。 ただし、 checkLineクラスについては引き続き作業します。

5）最初のサイクルを完了した後、「向きを変える」必要があります。 イテレータを中心に変換し、インデックス0で中央の攻撃を行い、攻撃の配列からそれを削除して現在の攻撃として設定します。

 turnAround(){ this.iter = 1; this.checkEdge = false; this.curAttack = this.Attacks[0]; this.Attacks.splice(0,1) } 

6）次に、現在のセルの反対側に移動して、反復子を増やします。
まったく同じ数字のチェック。 （コードはすでに記述されています-getAttacks関数）

7）すべて、1つのアレイのライン上にあったすべての攻撃を収集しました。
これでcheckLineクラスを使用すると、すべて...が完了します。

それでは、すべてが簡単です。各ライン（水平および垂直の2つの対角線）に対してcheckLineオブジェクトを作成し、 getAttacks関数を呼び出します。 つまり、 各行に対して-独自のcheckLineオブジェクトと、それに応じた独自の攻撃セット。

getAllAttacks（）関数がこれらすべてを担当します-すでに上記のクラスとは別に。

 getAllAttacks( cellX, cellY ){ // ,  , //       if( Model.Field[ cellX ][ cellY ] ) return false var cX = []; var cO = []; //   ... cX['0'] = this.getAttacksLine( cellX, cellY, '×', 1, 0 ); cX['90'] = this.getAttacksLine( cellX, cellY, '×', 0, 1 ); cX['45'] = this.getAttacksLine( cellX, cellY, '×', 1, -1 ); cX['135'] = this.getAttacksLine( cellX, cellY, '×', 1, 1 ); //  ... cO['0'] = this.getAttacksLine( cellX, cellY, '○', 1, 0 ); cO['90'] = this.getAttacksLine( cellX, cellY, '○', 0, 1 ); cO['45'] = this.getAttacksLine( cellX, cellY, '○', 1, -1 ); cO['135'] = this.getAttacksLine( cellX, cellY, '○', 1, 1 ); return { //     'x': cX, 'o': cO } } getAttacksLine( cellX, cellY, subFig, dx, dy ){ //      var C = new checkLine; C.getAttacks( cellX, cellY, subFig, dx, dy ); return this.filterAttacks( C ) //   } 

出力には、テスト対象のセルに対するすべての攻撃を含むオブジェクトがあります。

ただし、何らかのフィルター機能に気付いているかもしれません。 そのタスクは、「無駄な」攻撃をふるいにかけることです。

• ゼロの電力で（配列に入るかどうかはわかりません）
• スペースが不足している攻撃（攻撃場所<5）
• ゼロ電位。

ただし、攻撃のパワーが5より大きい場合、フィルターはそれをスキップします。 ボットはこのような攻撃を確認する必要があります。スクリーニングを行うと、ゲーム終了時に妨害が発生します。

 filterAttacks( attackLine ){ var res = [] if( attackLine.attackplace >= 5 ) attackLine.Attacks.forEach( ( a )=>{ if( a.capability && a.potential || a.capability >= 5 ) res.push( a ) }) attackLine.Attacks = res; return res } 

ブレークポイント

はい...再び、ごめんなさい！ したがって、1つの間違った動きがゲームの結果を決定するときに、ゲームの状況を呼び出します。

たとえば、攻撃[3：2]はブレークポイントです。 対戦相手が隣に駒を置いてそれをブロックしなかった場合、次の動きでは、すでにフィールドで攻撃[4：2]が行われています。

または攻撃[4：1]。 一あくび-そしてゲームは簡単に完了することができます。


図5.ブレークポイント

ここではすべてが明確で理解可能なものであり、上記のアルゴリズムはすでにブレークポイントを考慮し、タイムリーにそれらをブロックすることができます。 ボットは楽しみです。 彼は、次のターンで、敵が攻撃を作成できることを確認します[5：1]。たとえば、その体重は200です。これは、unningなオタクがここに行くことを意味します。

ただし、プレーヤーの1人がフィールドで2つのブレークポイントを取得する状況を想像してください。 そして、これは明らかに、相手にチャンスを残しません、なぜなら 一度にブロックできるブレークポイントは1つだけです。 このような攻撃をブロックするようにAIに教える方法は？


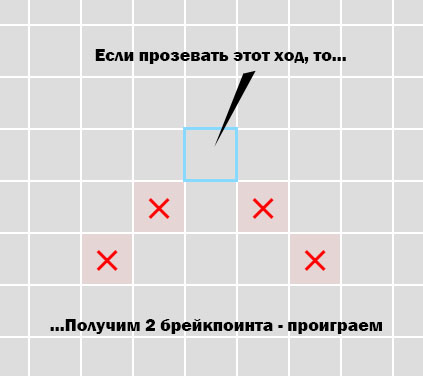図6. 2ブレークポイント

セルを分析するとき、セル内のピースを代入するとき、次のターンで取得するブレークポイントの数をカウントします（ボットは前方への動きを見て、忘れないでください）。 2つのブレークポイントをカウントすることにより、セルの重みを100増やします。

そして今、ボットはそのようなゲームの状況を防ぐだけでなく、それらを作成することができるようになり、より手ごわい相手になりました。

攻撃がブレークポイントであることを理解する方法

明白なことから始めましょう：4のべき乗を持つ攻撃はブレークポイントです。 たった1回のミスで、ゲームを完了する機会が与えられます。 5個を一列に並べます。

さらに、攻撃の可能性が2である場合、そのような攻撃をブロックするためにさらに1ターンを費やします。つまり、3のべき乗のブレークポイントが存在することを意味します。

そしてさらに難しい- 「引き裂かれた攻撃」 。
中央に空のセルが1つだけある攻撃のみを検討します。 これは、2つの空のセルを中央に配置して攻撃を完了するには、少なくとも2回の移動が必要であるためです-これは明らかにブレークポイントではありません。

私たちが思い出すように、私たちは破れた攻撃をいくつかの従来の攻撃と考えています：1つの中央攻撃とサイド攻撃です。 中央の攻撃はスキャンされたセルに属し、サイドディバイダーには1以上があります-これは上記のとおりです。

ブレークポイントを見つけるためのアルゴリズム（簡単、以下をお読みください）：

1. 可変スコアを紹介します
2. 私たちは中央攻撃を取り、力を考慮します
3. 除数が2倍以下の場合、サイドの1つを使用します。
4. スコア -中央およびサイド攻撃の力の合計
5. 中央およびサイド攻撃の可能性が2である場合、そのような攻撃をブロックするには、もう1ターンを費やす必要があります。 したがって、スコアは1増加します
6. スコアが 4以上の場合、これはブレークポイントです
   実際、ブレークポイントは単純に列挙することができ、それらの多くはありませんが、すぐにはわかりませんでした。

 isBreakPoint( attackLine ){ if( ! attackLine || ! attackLine.length ) return false; var centAtk; attackLine.forEach( ( a )=>{ if( a.divider == 1 ) centAtk = a; }) if( centAtk.capability >= 4 ) return true if( centAtk.potential == 2 && centAtk.capability >= 3 ) return true; var res = false; attackLine.forEach( ( a )=>{ var score = centAtk.capability; if( a.divider == 2 ){ //side attack if( centAtk.potential == 2 && a.potential == 2 ) score++; if( score + a.capability >= 4 ){ res = true; return; } } }) return res; } 

はい、最終的にすべてをまとめます

したがって、背後にある主な地獄については上で説明しています。 それから機能する何かを形作る時です。 関数countWeight（x、y） -セルの座標を入力として受け取り、その重みを返します。 彼女のフードの下には何がありますか？

最初に、セルが属するすべての攻撃の配列を取得します。 （ getAllAttacks（x、y） ）。 すべての行を調べて、ブレークポイントの数をカウントします。 2つのブレークポイントがある場合、この状況がゲームの結果を決定し、セルの重みを100増やすことができることを思い出してください。
ただし、すべてのブレークポイントは1人のプレーヤーに属している必要があるため、最初のクロス、次にゼロの2つのステップでチェックを実装する必要がありました。

攻撃の重みの配列（ ATTACK_WEIGHTS [] ）で6以上のパワーの攻撃を提供しなかったため、それらを5のパワーの攻撃に置き換える必要がありました。違いはありません。それらはすべてゲームの終わりにつながります。

さて、攻撃の重みを要約します-それだけです。

別の小さな点：ボットがゲームの終わりに馬鹿にならないように、既に4のべき乗で攻撃を構築し、現在の動きを考えている場合、そのような攻撃を完了するにはセルの重量を大幅に増やす必要があります。 これがなければ、AIは単純に、相手の「危険な」攻撃から身を守ることができますが、ゲームは勝ったように見えます。 最後の動きは重要です。

 countWeight( x, y ){ var attacks = this.getAttacks( x, y ) if( ! attacks ) return; var sum = 0; sum += count.call( this, attacks.x, '×' ); sum += count.call( this, attacks.o, '○' ); return sum function count( atks, curFig ){ var weight = 0; var breakPoints = 0; [ "0", "45", "90", "135" ].forEach( ( p )=>{ if( this.isBreakPoint( atks[p] ) ){ debug( "Break point" ) if( ++breakPoints == 2 ){ weight += 100; debug( "Good cell" ) return; } } atks[p].forEach( ( a )=>{ if( a.capability > 5 ) a.capability = 5; if( a.capability == 5 && curFig == Model.whoPlays.char ) weight += 100; weight += a.getWeight(); }); }) return weight } } 

ここで、特定のセルに対してこの関数を呼び出すと、その重みが取得されます。 すべてのセルに対してこの操作を実行し、最適なものを選択します（重みが最も高い）。 そこに行く）

残りのコードはgithubで見つけることができます。 すでに多くの資料があり、そのプレゼンテーションは、私が試したことがないので、望まれるものがたくさんあります。 しかし、読者の皆さん、ここまで読んでいただければ、ありがたいです。

結果に対する私の意見

さあ！はい、あなたは彼を倒すことができますが、それをすることは私にとって個人的に少し問題です。たぶん私は十分に注意していません。あなたの強さも試してください。

私はそれがより簡単に可能であることを知っていますが、私は方法がわかりません。このようなボットの他の実装を知っている、または見ている人の話を聞きたいです。

私は何が良くなるかを知っています。はい...ミニマックスなどの有名なアルゴリズムを使用できますが、そのためにはゲーム理論の分野で知識ベースが必要です。残念ながら、それは自慢できません。

将来的には、ブレークポイント分析を数ステップ先に追加して、ボットをさらに深刻なライバルにする予定です。しかし、現在、この実装について明確な考えがありません。私はちょうど今度のセッションと不完全な卒業証書を持っています-それは私を悲しませます。

最後まで読んでくれてありがとう。