最新のDDR3 SDRAM。 出典： BY-SA / 4.0 by Kjerish

マウンテンビューにあるコンピューター歴史博物館への最近の訪問中に、フェライトメモリの古代の例が注目を集めました。

出典： BY-SA / 3.0 by Konstantin Lanzet

私はそのようなことがどのように機能するのかわからないという結論にすぐに到達しました。リングが回転しますか（いいえ）、なぜ3本のワイヤが各リングを通りますか（私はまだそれらがどのように機能するか理解していません）。さらに重要なことは、最新のダイナミックRAMがどのように機能するのか、ほとんどわからないことです。

出典： Ulrich Drapper's Memory Cycle

私は、ダイナミックRAMがどのように機能するかの結果の1つに特に興味がありました。データの各ビットは、RAMチップ内の小さなコンデンサの電荷（またはその不在）によって保存されることがわかります。しかし、これらのコンデンサは時間とともに徐々に電荷を失います。保存されたデータの損失を避けるために、それらを定期的に更新して、課金（ある場合）を元のレベルに戻す必要があります。この更新プロセスでは、各ビットを読み取ってから書き戻します。この「更新」の間、メモリは占有され、ビットの書き込みや保存などの通常の操作を実行できません。

これは長い間私を悩ませ、私は疑問に思いました...プログラムレベルでの更新の遅れに気付くことは可能ですか？

ダイナミックRAMアップグレードトレーニングベース

各DIMMは、「セル」と「行」、「列」、「サイド」、および/または「ランク」で構成されます。ユタ大学からのこのプレゼンテーションでは、命名法を説明しています。コンピューターのメモリ構成は、 decode-dimmsで確認できます。以下に例を示します。

  $ decode-dimms
サイズ4096 MB
銀行x行x列xビット8 x 15 x 10 x 64
ランク2

DDR DIMMスキーム全体を理解する必要はありません。1ビットの情報を格納する1つのセルのみの動作を理解する必要があります。より正確には、更新プロセスにのみ関心があります。

2つのソースを検討してください。

ユタ大学DRAMアップデートチュートリアル
また、Micronのギガビットチップに関する優れたドキュメント：「1Gb DDR SDRAM用のTN-46-09の設計」

動的メモリの各ビットを更新する必要があります。これは通常64ミリ秒ごとに発生します（いわゆる静的更新）。これはかなり高価な操作です。 64ミリ秒ごとに1つの大きな停止を回避するために、プロセスは8192の小さな更新操作に分割されます。それぞれで、コンピューターのメモリコントローラーはDRAMチップに更新コマンドを送信します。命令を受け取った後、チップは1/8192セルを更新します。カウントすると、64 ms / 8192 = 7812.5 nsまたは7.81μsです。これは次のことを意味します。

更新コマンドは、7812.5 nsごとに実行されます。これはtREFIと呼ばれます。
更新および回復プロセスには時間がかかるため、チップは再び通常の読み取りおよび書き込み操作を実行できます。いわゆるtRFCは、75 nsまたは120 nsのいずれかに等しくなります（前述のMicronのドキュメントのように）。

メモリが高温（85°C以上）の場合、メモリのデータ保存時間は低下し、静的更新時間は32ミリ秒に半分になります。したがって、tREFIは3906.25 nsに低下します。

一般的なメモリチップは、その寿命のかなりの部分（0.4％から5％）の間、更新に追われています。また、メモリチップは一般的なコンピューターの電力消費の重要な部分を担っており、この電力のほとんどはアップグレードに費やされています。

更新中、メモリチップ全体がブロックされます。つまり、メモリ内の各ビットは、7812 nsごとに75 ns以上ロックされます。それを測定しましょう。

実験準備

ナノ秒の精度で操作を測定するには、おそらくCでの非常に短いサイクルが必要です。次のようになります。

  for (i = 0; i < ...; i++) { //   . *(volatile int *) one_global_var; //   CPU.    _mm_clflush(one_global_var); //   ,     //    (25    160). // , - . asm volatile("mfence"); //     clock_gettime(CLOCK_MONOTONIC, &ts); }

完全なコードはGitHubで入手できます。

コードは非常に簡単です。メモリ読み取りを実行します。 CPUキャッシュからデータをダンプします。時間を測定します。

（注： 2番目の実験では、 MOVNTDQAを使用してデータをロードしようとしましたが、これにはキャッシュ不可の特別なメモリページとルート権限が必要です）。

私のコンピューターでは、プログラムは次のデータを表示します。

  ＃タイムスタンプ、サイクルタイム
 3101895733、134
 3101895865、132
 3101896002、137
 3101896134、132
 3101896268、134
 3101896403、135
 3101896762、359
 3101896901、139
 3101897038、137

通常、約140 nsの期間のサイクルが取得され、定期的に約360 nsにジャンプします。時々、3200 nsを超える奇妙な結果が表示されます。

残念ながら、データはノイズが多すぎます。更新サイクルに関連する顕著な遅延があるかどうかを確認することは非常に困難です。

高速フーリエ変換

ある時点で、それは私に気づきました。一定の間隔でイベントを検索するため、基本周波数を解読するFFT（高速フーリエ変換）アルゴリズムにデータを送信できます。

私はそれについて最初に考えたわけではありません。有名な脆弱性を持つマーク・シーボーンは、2015年にこの技術を実装しました。 Markのコードを見た後でも、FFTを機能させるのは予想以上に困難でした。しかし、最終的には、すべてのピースをまとめました。

まず、データを準備する必要があります。 FFTには、一定のサンプリング間隔の入力が必要です。また、ノイズを減らすためにデータをトリミングします。試行錯誤により、データの予備処理後に最良の結果が得られることがわかりました。

ループ反復の小さな値（平均1.8未満）は切り捨てられ、無視され、ゼロに置き換えられます。私たちは本当に騒ぎたくありません。
他のすべての測定値は単位に置き換えられます。これは、ノイズによって引き起こされる遅延の振幅が本当に重要ではないためです。
100 nsのサンプリング間隔で解決しましたが、ナイキスト周波数（期待される2倍の周波数）までの任意の数で対応できます。
データは、FFTに送信する前に一定の時間にサンプリングする必要があります。妥当なサンプリング方法はすべて正常に機能するため、基本的な線形補間に決めました。

アルゴリズムは次のようなものです。

 UNIT=100ns A = [(timestamp, loop_duration),...] p = 1 for curr_ts in frange(fist_ts, last_ts, UNIT): while not(A[p-1].timestamp <= curr_ts < A[p].timestamp): p += 1 v1 = 1 if avg*1.8 <= A[p-1].duration <= avg*4 else 0 v2 = 1 if avg*1.8 <= A[p].duration <= avg*4 else 0 v = estimate_linear(v1, v2, A[p-1].timestamp, curr_ts, A[p].timestamp) B.append( v )

私のデータでは、このようなかなり退屈なベクトルを生成します：

  [0、0、0、0、0、0、1、0、0、0、0、0、0、0、0、0、0、0、0、 
  0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、1、1、0、
  0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、 
  0、0、1、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、...]

ただし、ベクトルは非常に大きく、通常は約20万のデータポイントです。このようなデータでは、FFTを使用できます！

 C = numpy.fft.fft(B) C = numpy.abs(C) F = numpy.fft.fftfreq(len(B)) * (1000000000/UNIT)

かなり簡単ですね。これにより、2つのベクトルが生成されます。

Cには、複素数の周波数成分が含まれています。複素数には興味がなく、 abs()コマンドを使用して複素数を滑らかにすることができます。
Fには、ベクトルCのどの場所にどの周波数スパンがあるラベルが含まれています。入力ベクトルのサンプリング周波数を乗算することにより、指数をヘルツに正規化します。

結果はチャートにプロットできます：

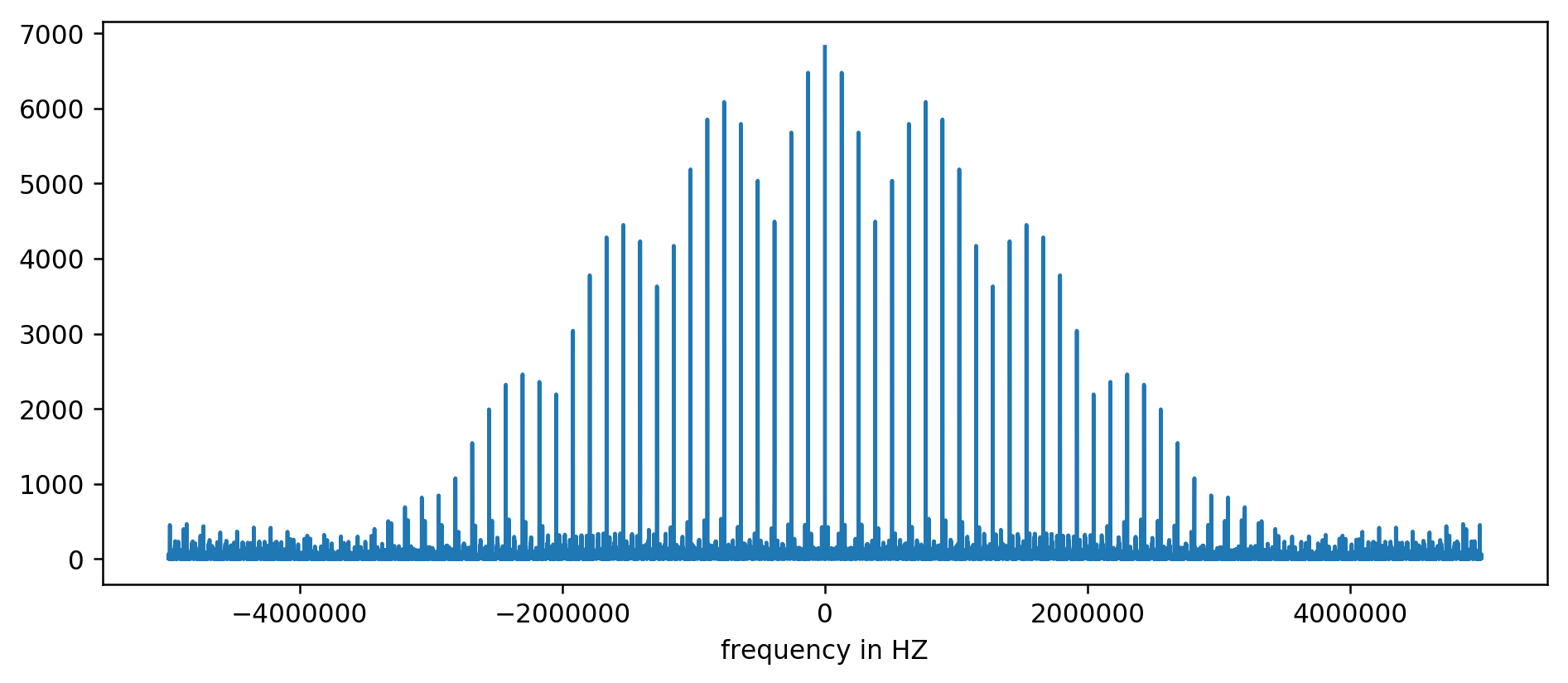
遅延時間を正規化したため、単位のないY軸。それにもかかわらず、いくつかの固定周波数範囲でバーストがはっきりと見えます。それらをより詳しく考えましょう：

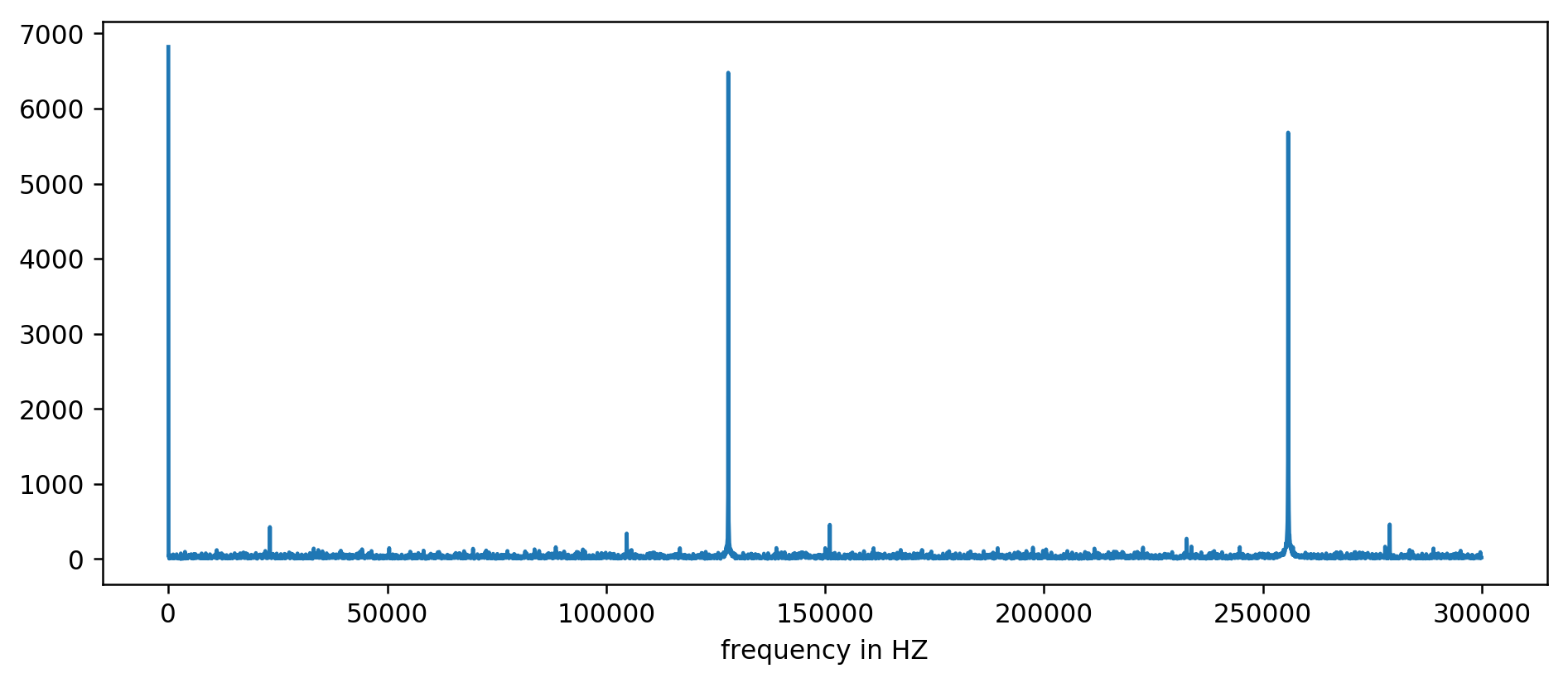
最初の3つのピークがはっきりと見えます。少なくとも平均の10倍の読み取り値をフィルタリングするなど、少し無意味な算術演算の後、基本周波数を抽出できます。

考慮する：1000000000（ns / s）/ 127900（Hz）= 7818.6 ns

やった！周波数の最初のジャンプは実際に私たちが探していたものであり、更新時間と本当に相関しています。

256 kHz、384 kHz、512 kHzの残りのピークはいわゆる高調波で、128 kHzの基本周波数の倍数です。これは、方形波のビットにFFTを適用することで完全に予期される副作用です。

実験を容易にするために、コマンドラインバージョンを作成しました。自分でコードを実行できます。これは私のサーバーで起動する例です：

  〜/ 2018-11-memory-refresh $ make
 gcc -msse4.1 -ggdb -O3 -Wall -Wextra measure-dram.c -o measure-dram
 ./measure-dram |  python3 ./analyze-dram.py
 [*] ASLRの検証：メイン= 0x555555554890スタック= 0x7fffffefe2ec
 []楽しい事実。  1秒あたり40663553 clock_gettime（）を実行しました
 [*] MOVQ + CLFLUSH時間の測定。  131072回の反復を実行しています。
 [*]データの書き出し
 [*]入力データ：min = 117 avg = 176 med = 167 max = 8172項目= 131072
 [*]カットオフ範囲212-inf
 []カットオフより下の127849アイテム、カットオフより上の0アイテム、非ゼロの3223アイテム
 [*] FFTの実行
 [*] 250kHz未満の2kHzを超える最高周波数の振幅は7716です
 [+] 2kHZを超える上位の周波数スパイクは次のとおりです。
 127906Hz 7716
 255813Hz 7947
 383720Hz 7460
 511626Hz 7141

コードは完全に安定しているわけではありません。問題が発生した場合は、ターボブースト、CPU周波数スケーリング、パフォーマンスの最適化を無効にすることをお勧めします。

おわりに

この作業から2つの主要な結論があります。

低レベルのデータは分析が非常に難しく、かなりうるさいようです。肉眼で評価する代わりに、いつでも古き良きFFTを使用できます。データの準備では、ある意味、希望的観測が必要です。

最も重要なことは、ユーザー空間の単純なプロセスから微妙なハードウェアの動作を測定できることが多いことを示しています。この種の考え方は、元のRowhammer脆弱性の発見につながり、Meltdown / Specter攻撃で実装され、最近のECCメモリのRowhammer生まれ変わりで再び示されました。

この記事の範囲をはるかに超えています。メモリサブシステムの内部操作についてはほとんど触れませんでした。さらに読むために、私はお勧めします：

最後に、古いフェライトメモリの説明を以下に示します。

シドニー大学のPDP-11フェライトメモリの説明

コンピューターのメモリは7.8μsごとに遅れます

ダイナミックRAMアップグレードトレーニングベース

実験準備

高速フーリエ変換

おわりに

More articles: