「ヒューストン、問題があります」と、夜にInvenSenseデータシートIMU MPU-9250を通り抜けようとして、頭の中で疲れた声がしました。 すべての単語が個別に理解可能であるが、それらの関係が不可能に混乱している場合。 それはすべてLSBパラメーターで始まりましたが、翻訳ではそれが最下位ビットであることを漠然としか覚えていませんでした。 その後、「解像度」、「感度」に進み、さらに、結果のテキストにはすでに「ダミーのデータシート」というタイトルが付けられていることに気付きました。
慣性モジュールの主要なブロックについて少し。
MEMSジャイロスコープ
MPU-9250は、X、Y、Z軸周りの回転に応答する3つの独立した単軸振動角速度センサー(MEMSジャイロスコープ)で構成されています。 2つの吊り下げられた質量が反対の軸で振動します。 角速度の出現により、コリオリ効果により振動の方向が変化します(
vecFK=−2m[ vec omega times vecvr] 静電容量センサーによって固定されています。 測定された差動容量成分は、動きの角度に比例します[Electronics Time]。 結果の信号は増幅、復調、フィルタリングされ、回転角速度に比例した電圧が得られます。 この信号は、オンボード16ビットADCを使用してデジタル化されます。 サンプルレートは、3.9〜8000サンプル/秒(サンプル/秒、SPS)からプログラムで変更でき、ユーザー定義のローパスフィルター(LPF)は、可能なカットオフ周波数の広い範囲を提供します。 ローパスフィルターは、特にモーターからの振動を除去するために必要です(原則として、20〜25 Hz以上)。
3軸MEMS加速度計
各軸に個別の試験質量を使用し、この軸に沿って加速度が発生すると変位します(静電容量センサーで固定)。 MPU-9250アーキテクチャは、温度ドリフトや電気パラメーターの変動への露出を低減します。 デバイスが平らな面にある場合、X軸とY軸に沿って0g、Z軸に沿って+ 1gを測定します。
スケールファクター (スケールファクター-出力測定信号の変化に対する出力信号の変化の比率)は、工場で較正されており、供給電圧に依存しません。 各センサーには個別のシグマ-デルタADC(変調器とデジタルローパスフィルターで構成され、[Easyelectronics]のデバイスの詳細)が装備されており、そのデジタル出力の測定範囲は調整可能です。
3軸MEMS磁力計について
高精度ホール効果技術に基づいています。 軸に沿った地球の磁場強度を決定する磁気センサー、制御回路、信号増幅回路、および各センサーからの信号を処理するための計算回路が含まれています。 各ADCの分解能は16ビットで、測定範囲があります
\午後4800 muT 。 弱い磁場を測定するには、マイクロテスラSIシステム(μT)またはガウス(G、GHSシステム)のいずれかのユニットを使用します。
1G.=100 muT 、[無線パイロット])。
LSBとは何ですか? 生産指示
加速度計が測定範囲で動作しているとしましょう
FS=\午後2g 、つまり、可能な値の全範囲は
2 cdotFS=4g 。 対応する電圧値は16ビットADCによってデジタル化され、インターバル全体を可能な限り分割できます。
216=65536 ステップ。 検出できる最小増分はわずか1ステップです
LSB=2 cdotFS/65536 。 ここでは、アカウントはゼロから実行されるため、実際には最大測定値は
2 cdotFStrue=(216−1)∗LSB=65535∗LSB=2 cdotFS−LSB 。 つまり、ADCまたはDACデジタルワードのビット数が多いほど、差異は小さくなります。 この場合、特定の範囲のセンサーの
感度(スケール係数、感度スケール係数とも呼ばれます)は、電気出力信号と機械的衝撃の比率として決定されます。 信号周波数100 Hzおよび温度に対して伝統的に示されています
T=+25 circC. MPU-9250の場合、感度は
216/(2 cdotFS) gごとのステップまたは
circ/s (
LSB/g 、
LSB/( circ/s) )、別のIMU、Bosch SensortecのBMI088の場合、ジャイロ感度は同じ方法で計算され、加速度計では使用されます
(216−24)/(2 cdotFS) 各gの手順

ジャイロスコープの仕様からFSバリアントを引き出し、2度起きないように加速度計を作成します。

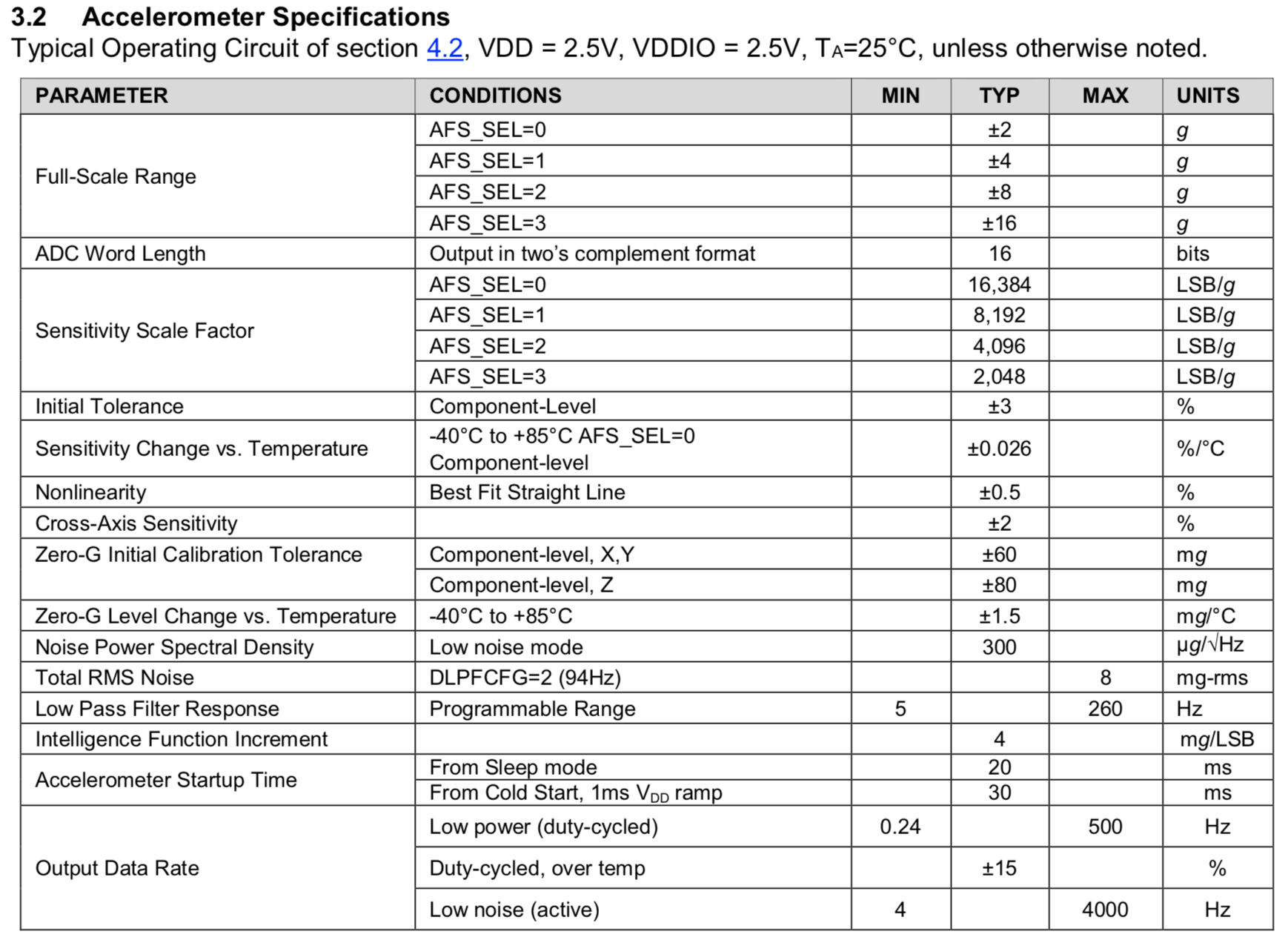
また、BMI088のドキュメントから加速度計のFSを取得しました(以下を参照)。
| ジャイロスコープ、16ビット (2N=65535) | 加速度計、16ビット (2N=65535) |
|---|
| 範囲(FS) circ/s (dps) | LSB、 circ/s (dps) | 範囲(FS)、g | LSB mg |
| \午後125 (FS = 250) | 0.004 | \午後2 (FS = 4) | 0.06 |
| \午後250 (FS = 500) | 0.008 | \午後3 (FS = 6) | 0.09 |
| pm500 (FS = 1000) | 0.0015 | \午後4 (FS = 8) | 0.12 |
| pm1000 (FS = 2000) | 0,03 | \午後6 (FS = 12) | 0.18 |
| pm2000 (FS = 4000) | 0.06 | \午後8 (FS = 16) | 0.24 |
| | \午後12 (FS = 24) | 0.37 |
| | \午後16 (FS = 32) | 0.48 |
| | \午後24 (FS = 48) | 0.73 |
すべてが適切な場所に落ちたようです。先に進むことができます。 場合によっては(たとえば、BMI088のドキュメントからの切り抜きなど)、解像度などのパラメーターが個別に示されます。
実際、LSBである必要があるようです。 しかし、なぜ特定の範囲に関連付けられたいくつかの値ではなく、1つの値が表示されるのでしょうか? 答えを探すために研究した情報源のリストを拡張する必要がありました。

解像度とは何ですか?
価格と性能のバランスをとろうとするとき、センサーが確実に見る最小値は非常に重要です。 これは正確ではありません。特定のエリアの低解像度センサーが十分な精度を持っているように、高解像度センサーは特に正確ではない場合があります。 残念ながら、LSBは、ADCの16ビットすべてを使用できる場合に限り、理論上の最小識別可能値のみを定義します。 これは、デジタルの世界における解決策です。 アナログでは、ステップの一部はノイズが多く、有効ビット数は少なくなります。
ノイズの特性は何ですか?それはどこから来ますか?
ノイズ源は一般に、動きを電圧信号に変換する回路の電子ノイズ(ジョンソン熱ノイズ、ショットノイズ、ピンク1 / fフリッカノイズなど)と機械的機械(小さな可動部品の存在によるブラウン)に分類できます。センサー自体から。 後者の特性は、システムの機械部分の共振周波数に依存します
f0 (センサーの固有振動周波数
omega0=2 pi/f0 )
スペクトル範囲全体のRMSノイズ-合計RMS(二乗平均平方根)ノイズ
ノイズレベルはいくつかの方法で決定できます。 それらは、時間または周波数領域(フーリエ変換後)で考慮することができます。 最初のケースでは、残留ノイズは固定センサーからの信号のrms値として取得されます(実際、これは、サンプリング時の標準偏差です
\上線x=0 )一定期間:
xRMS= sigmaX= sqrt sumni=1(xi− overlinex)2 overn−1
ブロードバンドノイズのレベル未満の加速度または角回転速度は区別できません。これが実際の解像度です。 交流電圧または交流のrms値(アクティブまたは有効と呼ばれることが多い)は、一定の信号の値に等しく、その信号の作用は、期間中にアクティブ(抵抗)負荷で同じ作業を実行します。 このアプローチは、ホワイトノイズが支配的なブロードバンドノイズを評価する場合に最も効果的です。
ホワイトノイズの場合、99.9%の確率でのrmsに対する振幅(瞬時ピーク値)の比は
NPP/NRMS=6.6 この比率は、クロスファクター(波高率、クロスレシオ)と呼ばれます。 95.5%の確率を選択できます-クロスファクターは4です。

実際、ノイズ信号はそれほどうまく動作せず、ピークを生成してクロスファクターを最大10倍にします。 一部の仕様では、値を見つけることができます
NPP または乗数自体。
0.1〜10 Hzの狭い低周波数帯域では、ピークトゥピークノイズ信号の振幅を使用して推定されるフリッカーノイズ「1 / f」が主な役割を果たします。
スペクトル密度
信号は、周波数ドメインで考慮する方が便利な場合があり、その説明は
スペクトルと呼ばれ
ます (周波数に対する振幅と位相の依存性)。 仕様で考えられるノイズの特性の1つは、ノイズの
パワースペクトル密度(PSD)、ノイズスペクトル密度、ノイズパワー密度、または単に
ノイズ密度と呼ばれ
ます )。 周波数範囲にわたるノイズパワーの分布を記述します。 電流または電圧による電気信号の表現に関係なく、負荷で消費される瞬間的な電力は正規化(R = 1オーム)でき、
p(t)= nu2(t)/R=i2(t)R=x2(t)。 一定期間にわたって信号によって消費される平均電力
(−T/2、T/2)、PTx= frac1T intT/2−T/2x2(t)\、dt。
電力はエネルギー入力の割合です。 決定された信号と非周期的な信号は、エネルギーによって決定されます。 周期的およびランダムな信号は、時間に制限されておらず、それに応じてエネルギーに制限がなく、任意の時点で平均電力がゼロではないため、電力の観点で表現されます
Px= limT to infty frac1T intT/2−T/2x2(t)\、dt。
[Sklyar]は、任意の周期信号が、増加する周波数を持つ無限数の高調波の組み合わせによって表現されることを思い出すことができます。
x( lambda)= fraca02+ sum inftyn=1(an cosn lambda+bn sinn lambda)、
コサインとサインを指数形式で表現した後
cos lambda= fracei lambda+e−i lambda2、 sin lambda= fracei lambda−e−i lambda2i
および交換
lambda= omegat=2 pif0t= frac2 pitT0 として書くことができます
x(t)= fraca02+ frac12 sum inftyn=1[(an−ibn)ein omegat+(an+ibn)e−in omegat]= sum inftyn=− inftycnein omegat、
ここで、フーリエ級数の複素係数(スペクトル成分)は
x(t) 、
$$ display $$ \ begin {equation} c_n = \ frac {1} {T_0} \ int ^ {T_0 / 2} _ {-T_0 / 2} x(t)e ^ {-in \ omega t}、dt = \ begin {cases} \ frac {1} {2}(a_n-ib_n)、&n> 0 \\ \ frac {a_0} {2}、&n = 0 \\ \ frac {1} {2}( a_n + ib_n)、&n <0 \ end {cases} \ end {equation} $$ display $$
一般的な場合、これらの係数は次のように表現できます。
cn=|cn|ei thetan、
|cn|= frac12 sqrta2n+b2n、 thetan= arctan left( fracbnan right)、b0=0、c0= fraca02。
振幅と位相スペクトルは、依存グラフと呼ばれます。
|cn| そして
thetan 周波数から。 パワースペクトル密度
PSD(f) 周期信号
x(t) 周波数範囲にわたる信号電力の分布を与えます:
PSD(f)= sum inftyn=− infty|cn|2 delta(f−nf0)
そして次元を持っています
[W/Hz]=[x2/Hz] 実際の信号の平均正規化電力は
Px= int infty− inftyPSD(f)、df。
非周期的なランダム信号(特に、ノイズ)は、限定的な意味で周期的であると説明できます。 もし
T0 無限になる傾向があり、一連のインパルスは個別のインパルスに変わります
x(t) 、スペクトル線の数は無限になる傾向があり、スペクトルグラフは滑らかな周波数スペクトルに変わります
X(f)。 この制限の場合、一対の積分フーリエ変換を決定できます
X(f)= int infty− inftyx(t)e−i2 pift、dt
そして
x(t)= int infty− inftyX(f)ei2 pift、df、
どこで
X(f) -フーリエ画像。
ランダム信号のパワースペクトル密度は、制限によって決定されます
PSD(f)= limT to infty frac1T|XT(f)|2.
周波数範囲での信号電力の分布について説明します。
定常状態のセンサーのホワイトノイズの平均はゼロであると仮定しているため(
\上線x=\上線x2=0 )、rms値の2乗は分散に等しく、正規化された負荷の合計電力を表します。
Noise2RMS= sigma2x=Px= int infty0PSD(f)、df= intBandwidth0PSD(f)、df=PSD(Badnwidth−0)
ノイズRMS= sqrtノイズ密度\帯域幅
私たちは仕様を調べます-実際には、対応する次元を持つその平方根がスペクトル密度の名前で示されています
[ circ/s/ sqrtHz] または
[ mug/ sqrtHz]。 つまり、読み取られた周波数帯域(帯域幅)を指定しないRMSノイズの値は無意味です。
帯域幅の選択についてもう少し
MEMSセンサーの出力で、異なる周波数の信号を取得します。 事前に測定しているプロセスについて一定の考えがあると想定されます。 たとえば、ドローンの加速度ベクトルを決定する場合、ノイズはデバイスの振動です。 指定した周波数(200 Hzなど)を超えるすべての周波数を遮断するローパスフィルターを使用して、有用な信号から分離できます。 MPU-9250は、マジック名
DLPFCFGのパラメーターを使用して、ローパスフィルターのカットオフ周波数を調整する機能を提供します。 これは、デジタルローパスフィルター構成の略です。 さらに仕様では、神秘的なタイプの表現(DLPFCFG = 2、92Hz)があちこちに現れましたが、デコードするためには、別のドキュメント「Register Map and Descriptions」に登らなければなりませんでした。 希望する効果を得るには、どのレジスタにどのビットのセットを書き込む必要があるかを示します。
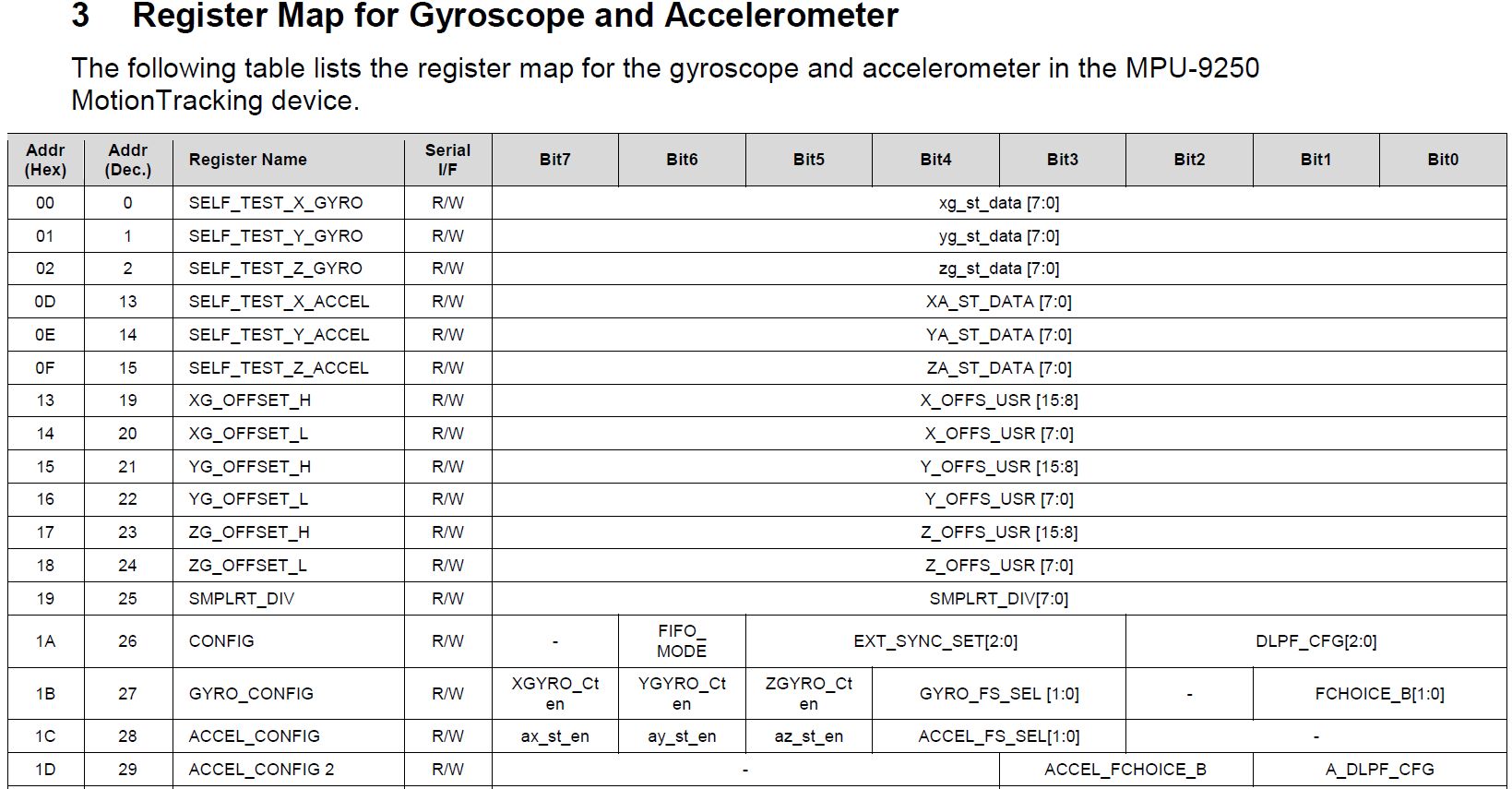
構成の技術的な詳細を省略すると、次のことが言えます。 このセンサーでは、加速度計、ジャイロスコープだけでなく、温度センサーの読み取り値のカスタマイズ可能なフィルタリングが実行されます。 それぞれについて、合計7〜10のモードがあり、Hz単位の帯域幅、ms単位の遅延、kHz単位のサンプリング周波数(Fs)などの概念によって特徴付けられます。

加速度センサーのフィルターモードの表では、列の「ノイズ密度」
m u g / r t H z = m u g / s q r t H z 、および「帯域幅」列に値「3dB」が追加されました。
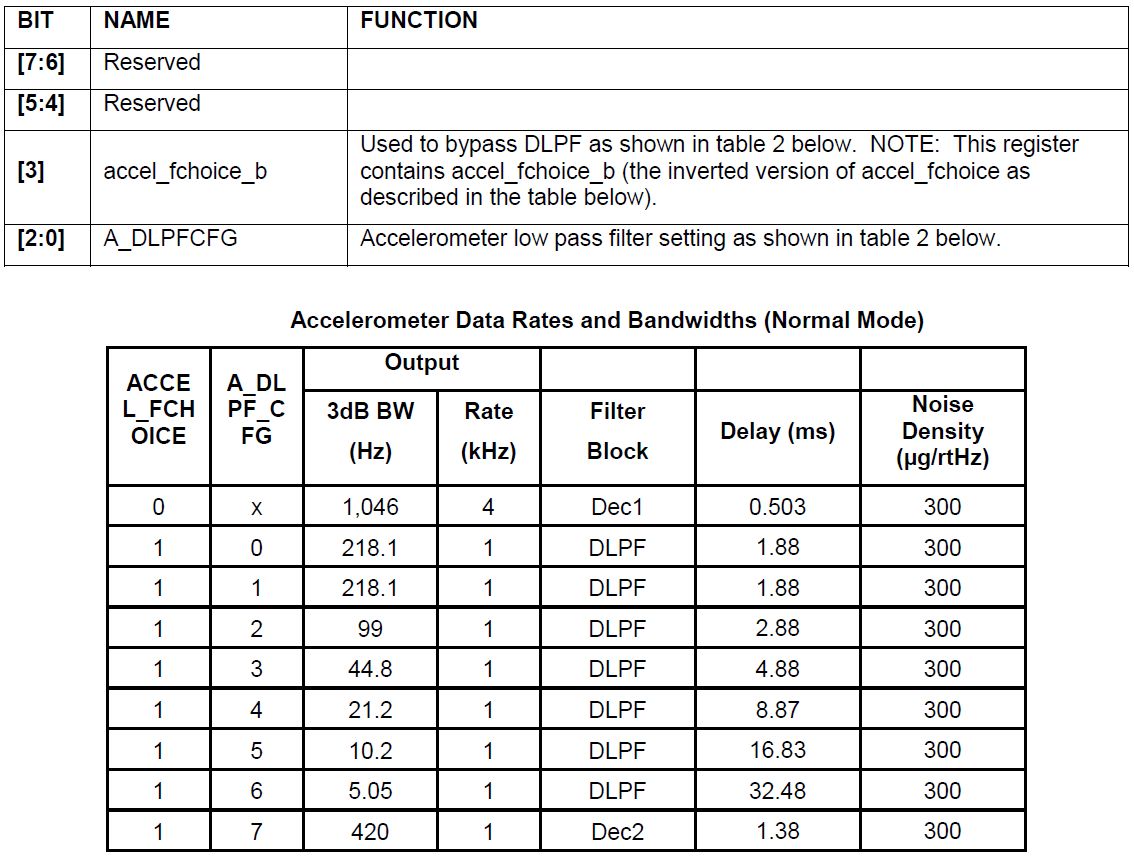
それは簡単ではないので、リストをまっすぐ見ていきましょう。
古代ローマの遺産
サンプリングレート+間引き \デルタ \シブログマ ADC =デジタル出力データレート(ODR)サンプリング周波数(サンプリング周波数)を使用すると、すべてが明確になります。これは、ADCによるサンプリング中に1秒あたりに取得される時間連続信号のポイント数です。 ヘルツで測定。
F s = f r a c 1 d e l t a t
信号のピーク振幅に近い値を取得するには、有効な信号の周波数の少なくとも10倍のサンプリング周波数を取得することが重要です。 MPU-9250には、Fs = 32kHz、8kHz、1kHzの3つのオプションがあります。
しかし、これは絶対に加速度計またはジャイロスコープの出力の信号が同じ周期で現れることを意味するものではありません。
同じドローンを使用する場合、エネルギー消費を削減し、計算速度を上げ、出力データのノイズを削減するための努力がすべて必要です。 内部アルゴリズムが一定期間にわたって入力情報を統合できるようにすることで、出力データの更新頻度を減らすことができます。 RMS値は減少しますが、帯域幅も狭くなります(センサーは、周波数がデータ更新レートの50%未満のプロセスのみを検出できます)。
ここでは、
コテルニコフの定理をすぐに思い出す方が良いでしょう。 アナログ信号をサンプリングするとき、有用な信号の周波数が
ナイキスト周波数とも呼ばれるサンプリング周波数の半分以下であれば、情報の損失を回避できる(つまり、信号を歪みなしに復元できる)と約束してい
ます 。 実際には、古典的なアンチエイリアシングフィルター(出力信号の2次周波数成分の影響を無視できるレベルに減らすローパスフィルター-GOST R 8.714-2010)は、ほとんどの場合、少なくとも2.5倍の差を必要とします[シーメンス]。
Fs = 32kHzの場合、ナイキスト周波数は16kHzになります。 同時に、有用な信号が帯域fa = 20Hzを超えることはほとんどありません(動きの方向を1秒あたり20回以上変更できるものはほとんどありません)。 合計すると、サンプリング周波数はfa帯域に含まれる情報を保存するのに必要な周波数よりもかなり高く(40Hz、400倍)、つまり、有用な信号がオーバーサンプリングされます。 周波数faとfs-faの間の帯域には、有用な情報は含まれていません。 サンプル(サンプル)のシーケンスを間引くことで、サンプリングレートを下げることができます(これは図の係数Mで行われました[7])。 このプロセスは
間引きと呼ばれます。
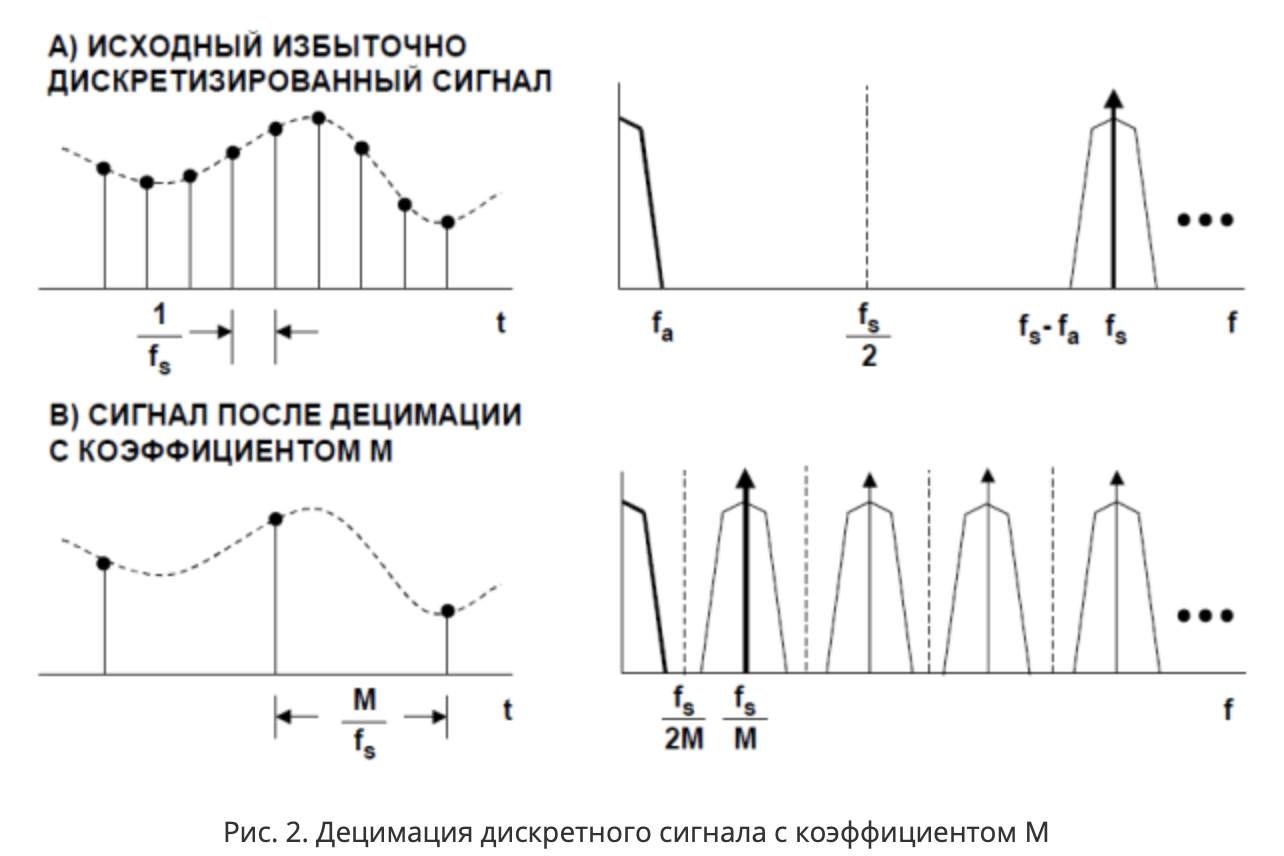
MPU-9250の仕様によると、加速度計には
シグマ-デルタADCが搭載されています。 それに基づくスキームは最小限の電力を消費します。 これらのコンバーターの帯域幅は非常に狭く、音域を超えない[Easyelectronics]が、標準のクワドロコプターの場合、これ以上は必要ないことに注意してください。 それらは2つのブロックで構成されます。
\シブログマ \デルタ -変調器およびデジタルデシメーションローパスフィルタ。
なぜローパスフィルターとデシメーションを組み合わせるのですか?
ウィキからの正直な抜粋:
元の信号に間引き信号のナイキスト周波数よりも高い周波数が含まれていない場合、受信(間引き)信号のスペクトル形状は、元の信号のスペクトルの低周波部分と一致します。 新しいサンプリングシーケンスに対応するサンプリングレートは、元の信号のサンプリング周波数のN倍です。
元の信号に、間引きされた信号のナイキスト周波数よりも高い周波数が含まれている場合、間引きによりエイリアシング(スペクトルの重ね合わせ)が発生します。
したがって、スペクトルを保存するには、デシメーションの前に、デシメートされた信号のナイキスト周波数よりも高い元の信号周波数から除去する必要があります。 MPU-9250仕様にはDLPFの特性に関する多くの情報は含まれていませんが、愛好家による研究は見つかります[9]。
帯域幅、周波数応答(周波数応答)
センサーが動きを検出し、有効な出力信号を提供する周波数範囲。 いくつかの仕様では、センサーの周波数応答が与えられます-加速度計の電気出力の外部機械的影響への依存性は、固定振幅で異なる周波数を持ちます。 帯域幅内では、周波数応答の不均一性は所定の値を超えません。 デジタルローパスフィルターを使用する場合、通過帯域を選択するだけでカットオフ周波数を変更できるため、空間の位置の変化に対するセンサーの応答速度に必然的に影響します。 カットオフ周波数は、ナイキスト周波数とも呼ばれるデジタル出力データレート(ODR)の半分未満でなければなりません。
MPU-9250加速度計の場合、帯域幅の境界は、範囲内で信号のスペクトル密度がピーク(周波数0 Hz)から-3 dB以下だけ変わらないように決定されます。
このレベルは、スペクトル密度の半分(またはピークスペクトル振幅の70.7%)への低下にほぼ相当します。デシベルで表される電界強度値の2乗に比例するエネルギー量(電力、エネルギー、エネルギー密度)については、比率を思い出させてくださいD P = 10 log P 2P 1
。
結論:ローパスフィルターを通過する信号のノイズは少なく、解像度は向上しますが、帯域幅は小さくなります。したがって、帯域幅を参照せずに仕様で解像度を指定しても意味がありません。解像度に戻る
MPU-9250の仕様では、解像度に関する情報は基本的にありません。BMI088の名前は「Resolution」であり、デジタル解像度(LSB)および感度が示さ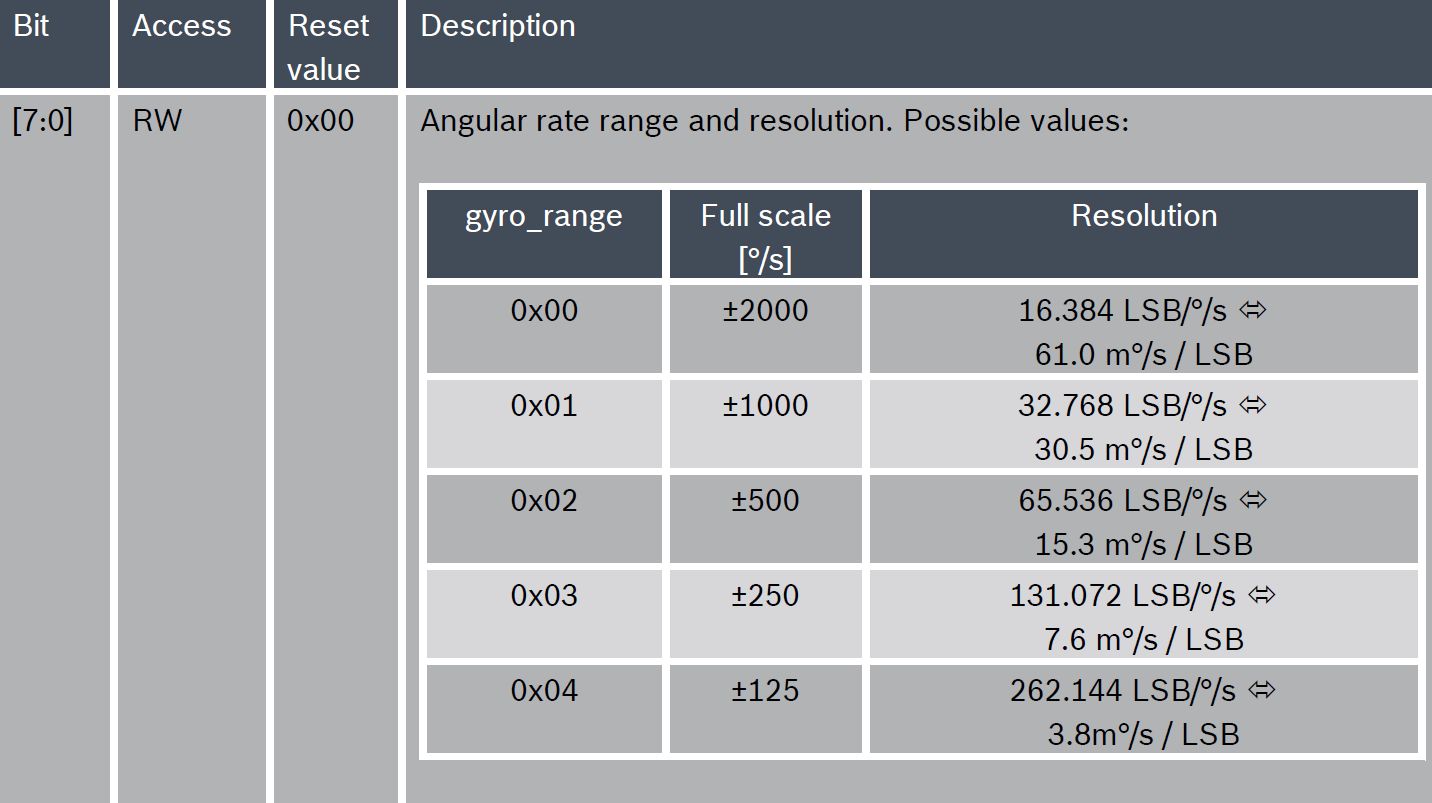 れています。Noisepk−pk=TotalNoiseRMS×CrestFactor=TotalNoiseRMS×4. 出力でのノイズの二乗平均値は、仕様に示されているスペクトル密度(またはそのルート)と等価ノイズ帯域幅(等価ノイズ帯域幅、ENBW)-矩形周波数応答とゼロ周波数で元のシステムと同じ値を持つ等価システムの通過帯域に関連していますホワイトノイズシステムの入力にさらされたときの出力での分散):
れています。Noisepk−pk=TotalNoiseRMS×CrestFactor=TotalNoiseRMS×4. 出力でのノイズの二乗平均値は、仕様に示されているスペクトル密度(またはそのルート)と等価ノイズ帯域幅(等価ノイズ帯域幅、ENBW)-矩形周波数応答とゼロ周波数で元のシステムと同じ値を持つ等価システムの通過帯域に関連していますホワイトノイズシステムの入力にさらされたときの出力での分散):N R M S = P S D × √E N B W
また、ノイズ帯域幅は、ローパスフィルターの次数に対応する係数によって3dB帯域に接続されます。E N B W = 1.57 ⋅ F 3 次元B 1オーダーの
E N B W = 1.11 ⋅ F 3 次元B 2次用
E N B W = 1.05 ⋅ F 3 D B 3次ため
E N B W = 1,025 ⋅ F 3 D B 4次ため
[MPU9250_DLPF]の調査から判断すると、私たちの選択は1.57です。得られたrms値は、ホワイトノイズの寄与を考慮します(量子化ノイズまたは機械ノイズはありません)。たとえば、加速度計の場合、計算された値B W = 99 のH Z 、P S D = 300 μ G / √H zが得られますN R M S = 4 m g 。
この場合、仕様には合計rmsノイズが含まれます T o t a l R M S N o i s e = 8 m g 。不一致は重大です。残念ながら、それは1つのバンドのみに示されており、BMI088加速度計には、仕様にPSDのみが示されています。だから私たちは何を使用します。クロスファクター4を見てみましょう。態度F S / N o i s e p k - p kは、この測定範囲での有効ビットのおおよその順序を提供します。これは、ADCの16ビット分解能よりもかなり小さいです。| MPU-9250 | BMI088 |
|---|
| ジャイロスコープ |
|---|
| NTotalRMS=0.1∘/s(BW=92Hz) | NRMS=0.1∘/s(BW=47Hz) |
|---|
| PSD=0.01∘/s/√Hz | PSD=0.014∘/s/√Hz |
|---|
| BW,Hz | NRMS,∘/s−rms | NPP,∘/s | BW,Hz | NRMS,∘/s | NPP,∘/s |
| | | 523 | 0.41 | 1.6 |
| 250 | 0.2 | 0.8 | 230 | 0.27 | 1.1 |
| 184 | 0.17 | 0.69 | 116 | 0.19 | 0.76 |
| 92 | 0.12 | 0.49 | 64 | 0.14 | 0.57 |
| 41 | 0.08 | 0.32 | 47 | 0.12 | 0.49 |
| 20 | 0.06 | 0.23 | 32 | 0.1 | 0.4 |
| 10 | 0.04 | 0.16 | 23 | 0.09 | 0.34 |
| 5 | 0.03 | 0.11 | 12 | 0.06 | 0.25 |
|
|---|
| NTotalRMS=8mg (BW=99Hz) | PSDXY=160μg/√Hz |
|---|
| PSD=300μg/√Hz (Gyro off) | PSDZ=190μg/√Hz(gFS3g, Normal mode) |
|---|
| BW,Hz | NRMS,mg | NPP,mg | BW,Hz | NRMSXY,mg | NPPXY,mg |
| 218.1 | 5.6 | 22 | 280 | 3.4 | 14 |
| 99 | 3.8 | 15 | 145 | 2.4 | 10 |
| 44.8 | 2.5 | 10 | 80 | 1.8 | 7 |
| 21.2 | 1.7 | 7 | 40 | 1.3 | 5 |
| 10.2 | 1.2 | 4.9 | 20 | 0.9 | 4 |
| 5.05 | 0.9 | 3.4 | 10 | 0.6 | 2.6 |
| 420 | 7.8 | 31 | 5 | 0.5 | 1.8 |
| 1046 | 12.3 | 49 | | | |
遅延(ミリ秒)、または遅延の発生源
異なる周波数で信号をフィルターで除算するために、変数を内部バッファーに保存する必要があるため
合計 フィルターのカットオフ周波数が低いほど、信号のノイズは少なくなります。 ただし、ここで注意する必要があります。同時に遅延が大きくなるためです。 さらに、有用なシグナルをスキップできます[8]。
| MPU-9250 | BMI088 |
|---|
| ジャイロスコープ、16ビット |
|---|
| 範囲(FS) circ/s (dps) | 解像度、ビット(BW = 92Hz) | 範囲(FS) circ/s (dps) | 解像度、ビット(BW = 64Hz) |
| | \午後125 | 8 |
| \午後250 | 9 | \午後250 | 9 |
| pm500 | 10 | pm500 | 10 |
| pm1000 | 11 | pm1000 | 11 |
| pm2000 | 12 | pm2000 | 12 |
| 加速度計 |
|---|
| 範囲(FS)、g | 解像度、ビット (NPP=32mg) | 範囲(FS)、g | 解像度(X、Y)、ビット (NXPPY=14mg) |
| \午後2 | 6 | \午後3 | 8 |
| \午後4 | 7 | \午後6 | 9 |
| \午後8 | 8 | \午後12 | 10 |
| \午後16 | 9 | \午後24 | 11 |
そして、これらは最も基本的なパラメーターです。
それはどこから来たのですか:
- フリースケールセミコンダクタの最も楽しいドキュメントは「How many Bits is Enough?」です。
- [EE]- 「混乱を切り抜ける解像度vs精度vs感度」
- [Electronics Time]- 「STMicroelectronicsのMEMSモーションセンサー:加速度計とジャイロスコープ」
- [LSB]- 「ADCおよびDAC最下位ビット(LSB)」
- [Measurement Computing]- 「TechTip:精度、精度、解像度、および感度」
- [KIT]- 「Analog Devices Accelerometers-Device and Application」
- [Easyelectronics]- 「シグマデルタADC」
- [Radiolotsman]- 「磁力計:動作原理、誤差補正」
- [SO]- 「ノイズ測定」
- [Mide]- 「加速度計の仕様:加速度計のデータシートを解読する」
- [CiberLeninka]- デルタシグマADCフィルター
- [SciEd]- 「サンプリング周波数の変更を伴うデジタルフィルタリングの実装の機能」
- [MPU6050]- 「MPU6050のDLPFの使用」
- [MPU9250_DLPF] -MPU9250ジャイロノイズDLPF作業調査
- センサー解像度の仕様について
- シーメンスデジタル信号処理
- STMicroelectronicsのMEMSモーションセンサー
- [TMWorld]- 「慣性測定ユニットの評価」
- [Sklyar]-Sklyar B.デジタル通信。 理論的基礎と実用化。