はじめに
このトピックに直接または間接的に関連するいくつかの記事[1,2,3]がHabrで公開されています。 この点で、最適なLQRコントローラーの動作原理を一般的に説明している「指の数学:線形二次レギュレーター」というタイトルの出版物[1]に注意を払うことはできません。
動的最適化手法の実用的なアプリケーションを検討して、このトピックを続けたいと思っていましたが、すでにPythonを使用した具体的な例でした。 まず、動的最適化の用語と方法に関するいくつかの言葉。
最適化方法は静的と動的に分けられます。 制御オブジェクトは、さまざまな外部および内部要因の影響下で連続的に移動する状態にあります。 したがって、制御結果の評価は制御時間Tに対して行われ、これが動的最適化のタスクです。
動的最適化の方法を使用すると、一定期間にわたる限られたリソースの分布に関連する問題が解決され、目的関数は積分関数として記述されます。
このような問題を解決するための数学的装置は変分法です:古典的な変動の計算、最大原理L.S. ポントリャーギンと動的プログラミングR.ベルマン。
制御システムの分析と合成は、時間、周波数、および状態空間で実行されます。 状態空間での制御システムの分析と統合はカリキュラムに導入されますが、SQRコントローラーを使用したトレーニング資料に示されている手法はMatlab用に設計されており、実用的な分析例は含まれていません。
この出版物の目的は、Pythonプログラミング言語を使用して電気駆動と航空機の制御システムを最適化するよく知られた例を使用して、状態空間での線形制御システムの分析と合成の方法を検討することです。
動的最適化手法の数学的実証
最適化には、振幅(MO)、対称(CO)、および妥協最適(KO)の基準が使用されます。
状態空間で最適化問題を解くとき、線形定常システムはベクトル-行列方程式で与えられます:
\ドットx= fracdxdt=A cdotx+B cdotu;y=C cdotx、 (1)
最小制御エネルギー消費量と最大速度の統合基準は、機能によって設定されます。
Jx= int infty0(xTQx+uTRu+2xTNu)dt\右矢印min、 (2)
Ju= int infty0(yTQy+uTRu+2yTNu)dt\右矢印min。 (3)
制御法則uは、状態変数xまたは出力変数yに対する線形フィードバックの形式です。
u= pmKx、u= pmKyこのような制御により、2次品質基準が最小化されます(2)、(3)。 関係(1)÷(3)では、QとRはそれぞれ次元[n×n]と[m×m]の対称正定行列です。 Kは次元[m×n]の定数係数の行列で、その値は制限されていません。 入力パラメーターNを省略すると、ゼロと見なされます。
状態空間での線形積分2次最適化(LQR最適化)問題と呼ばれるこの問題の解は、次の式で決定されます。
u=R−1BTPxここで、行列Pはリカッティ方程式を満たさなければなりません。
ATP+PA+PBR−1BTP+Q=0条件(2)、(3)も矛盾しています。これは、最初の用語の実装には無限に高い電力のソースが必要であり、2番目の用語には無限に低い電力のソースが必要だからです。 これは次の式で説明できます。
Jx= int infty0xTQxdt 、
これは標準です
Mod(x) ベクトルx、つまり 規制の過程での振動の尺度であり、したがって、振動が少ない高速過渡状態ではより小さな値を取り、式:
Ju= int infty0uTRudtそれを制御するために使用されるエネルギー量の尺度であり、これはシステムのエネルギーコストに対するペナルティです。
重み行列Q、R、およびNは、対応する座標の制約を決定します。 これらの行列のいずれかの要素がゼロに等しい場合、対応する座標には制限がありません。 実際には、行列Q、R、Nの値の選択は、専門家による推定、試行、エラーの方法によって実行され、設計エンジニアの経験と知識に依存します。
このような問題を解決するために、次のMATLAB演算子が使用されました。
beginbmatrixR、S、E endbmatrix=lqr(A、B、Q、R、N) そして
beginbmatrixR、S、E endbmatrix=lqry(Ps、Q、R、N) 関数(2)、(3)を状態ベクトルxまたは出力ベクトルyによって最小化します。
管理オブジェクトモデル
Ps=ss(A、B、C、D) 計算の結果は、状態変数xに対する最適なフィードバックの行列K、リカッティ方程式Sの解、および閉ループ制御システムの固有値E = eiq(A-BK)です。
機能コンポーネント:
Jx=x0TP1x0、Ju=x0TP2x0x0は初期条件のベクトルです。
P1 そして
P2 -リアプノフ行列方程式の解である未知の行列。 それらは関数を使用して検出されます。
P1=lyap(NN、Q) そして
P2=lyap(NN、KTRK) 、
NN=(A+BK)TPythonを使用した動的最適化手法の実装の機能
Python Control Systems Library [4]には関数control.lqr、control.lyapがありますが、control.lqrの使用は、slycotモジュールがインストールされている場合にのみ可能です。これは問題です[5]。 タスクのコンテキストでlyap関数を使用する場合、最適化によりcontrol.exception.ControlArgumentが発生します。Qは対称行列エラーでなければなりません[6]。
したがって、lqr()およびlyap()関数を実装するために、scipy.linalgを使用しました。
from numpy import* from scipy.linalg import* def lqr(A,B,Q,R): S =matrix(solve_continuous_are(A, B, Q, R)) K = matrix(inv(R)*(BT*S)) E= eig(AB*K)[0] return K, S, E P1=solve_lyapunov(NN,Ct*Q*C)
ところで、関数step()、pole()、ss()、tf()、feedback()、acker()、place()などがうまく機能するため、制御を完全に放棄すべきではありません。
電気駆動でのLQR最適化の例
(例は出版物[7]から取られます)行列によって状態空間で定義された制御オブジェクトの基準(2)を満たす線形2次コントローラーの合成を考えます。
A= beginbmatrix&−100&0&0&143.678&−16.667&−195.402&0&1.046&0 endbmatrix;B= beginbmatrix230000 endbmatrix;C= beginbmatrix1&0&00&1&00&0&1 endbmatrix;D=0
以下は状態変数と見なされます。
x1 -コンバータ電圧、V;
x2 -モーター電流、A;
x3 -角速度
c−1 。 これは、TP-HBを備えたDPTシステムです。エンジンR nom = 30 kW。 Unom = 220 V; Inom = 147 A ;;
\オメガω 0 = 169
c−1 ;
\オメガω 最大= 187
c−1 ; 公称抵抗モーメントMnom = 150 N * m; 開始電流の多重度= 2; サイリスタコンバータ:Unom = 230 V; Uy = 10 B; Inom = 300 A; 短時間の過電流の多重度= 1.2。
問題を解くとき、行列Q対角を受け入れます。 モデリングの結果、行列要素の最小値R = 84であり、
Q=[[0.01,0,0]、[0、0.01,0]、[0,0,0.01]]。 この場合、エンジンの角速度の単調遷移プロセスが観察されます(図1)。 R = 840で
Q=[[0.01,0,0]、[0、0.01,0]、[0,0,0.01]] 過渡プロセス(図2)はMO基準を満たしています。 行列P1およびP2の計算は、x0 = [220 147 162]で実行されました。
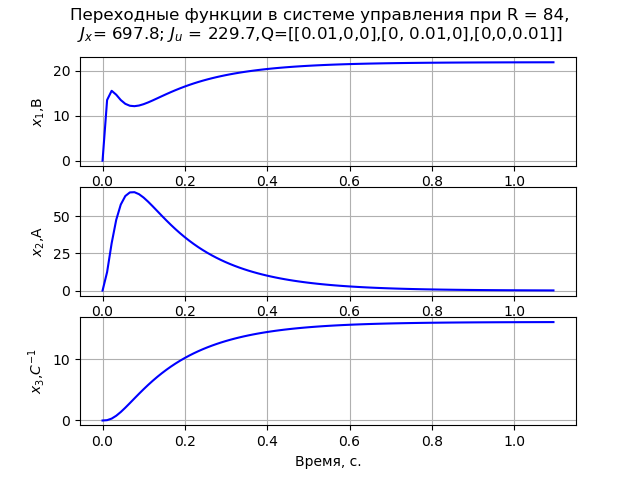 図 1
図 1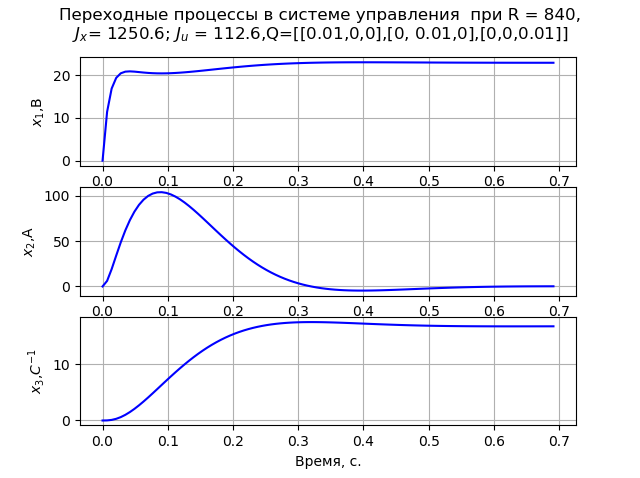 図 2
図 2マトリックスRとQを適切に選択することにより、モーターの始動電流を(2–2.5)Inに等しい許容値に減らすことができます(図3)。 たとえば、R = 840および
Q =([[[0.01,0,0]]、[0,0.88,0]、[0,0,0.01]]、その値は292 A、これらの条件下での遷移プロセス時間は1.57秒です。

図3
考慮されるすべての場合において、電圧と電流のフィードバックは負であり、フィードバック速度は正であり、これは安定性の要件に従って望ましくありません。 さらに、合成されたシステムは、タスクに対して静的であり、負荷に対して静的です。 したがって、状態変数を追加した状態空間でのPIコントローラーの合成を検討します
x4 -積分器の伝達係数。
初期情報を行列形式で表します。
A= beginbmatrix&−100&0&0&0&143.678&−16.667&−195.402&0&0&1.046&0&0&0&0&1&0 endbmatrix;B= beginbmatrix2300000 endbmatrix;C=eye(4));D=0MO基準に対応するタスクトランジェントは、R = 100、q11 = q22 = q33 = 0.001、およびq44 = 200で得られました。図4は、タスクごとおよび負荷ごとのシステムの非定常性を確認する状態変数トランジェントを示しています。
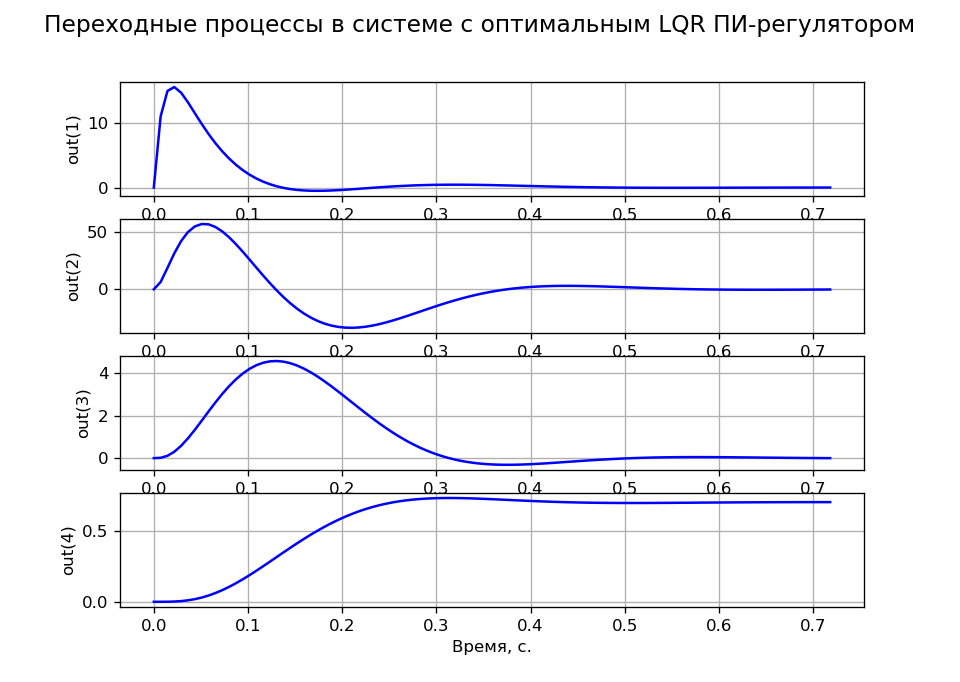 図 4
図 4行列Kを決定するために、Python制御システムライブラリには2つの関数K = acker(A、B、s)とK = place(A、B、s)があります。ここで、sはベクトル-閉ループ制御システムの伝達関数の目的の極の行です。 最初のコマンドは、n≤5のuに1つの入力があるシステムでのみ使用できます。 2番目にはこのような制限はありませんが、極の多重度は行列Bのランクを超えてはなりません。acker()演算子の使用例はリストと(図5)に示されています。
 図 5
図 5おわりに
新しいlqr()およびlyap()関数の使用を考慮に入れた、出版物に示されているLQRドライブ最適化の実装により、制御理論の対応するセクションを研究する際に、ライセンスプログラムMATLABの使用を放棄することができます。
航空機でのLQR最適化の例(LA)
(例は、Astrom and Mrurayの第5章[8]の出版物から取られ、lqr()関数を置き換え、用語を一般に受け入れられているものに減らすという点で記事の著者によって最終決定されました)理論部分、簡単な理論、LQRの最適化については既に上記で検討したため、対応するコメントを使用してコード分析に移りましょう。
必要なライブラリとLQRコントローラー機能。 from scipy.linalg import*
初期条件と基本行列A、B、C、Dモデル。 xe = [0, 0, 0, 0, 0, 0];
xy位置の段階的な変化に対応する入力と出力を作成します。 ベクトルxdおよびydは、システムの目的の定常状態に対応します。 行列CxおよびCyは、モデルの対応する出力です。 システムのダイナミクスを説明するには、ベクトル行列方程式のシステムを使用します。
\ left \ {\ begin {matrix} xdot = Ax + Bu => xdot =(A-BK)x + xd \\ u = -K(x-xd)\\ y = Cx \\ \ end {matrix} \右。
\ left \ {\ begin {matrix} xdot = Ax + Bu => xdot =(A-BK)x + xd \\ u = -K(x-xd)\\ y = Cx \\ \ end {matrix} \右。
閉ループのダイナミクスは、入力ベクトルとしてK \ cdot xdおよびK \ cdot xdのstep()関数を使用してモデル化できます。ここで、
xd = matrix([[1], [0], [0], [0], [0], [0]]); yd = matrix([[0], [1], [0], [0], [0], [0]]);
現在のコントロール0.8.1ライブラリは、フィードバックコントローラーを作成するためのSISO Matlab関数の一部のみをサポートしているため、コントローラーからデータを読み取るには、横方向-xおよび縦方向-yダイナミクスのインデックスベクトルlat()、alt()を作成する必要があります。
lat = (0,2,3,5); alt = (1,4);
各タスクのスケジュールを1つずつ決定します。
figure(); title(" x y") plot(Tx.T, Yx.T, '-', Ty.T, Yy.T, '--'); plot([0, 10], [1, 1], 'k-'); axis([0, 10, -0.1, 1.4]); ylabel(' '); xlabel(''); legend(('x', 'y'), loc='lower right'); grid() show()
チャート: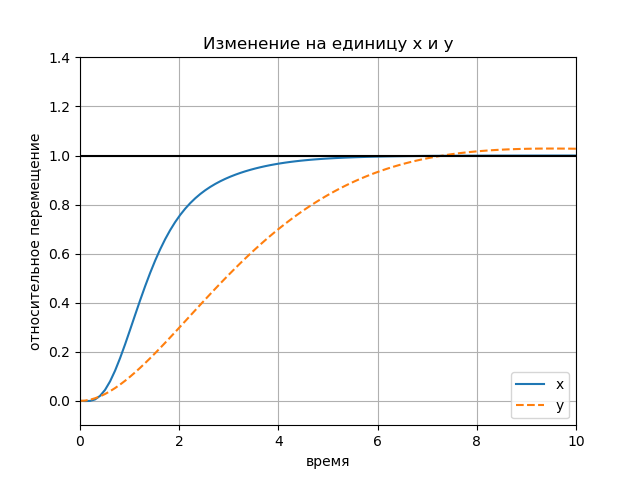 チャート:
チャート: チャート:
チャート: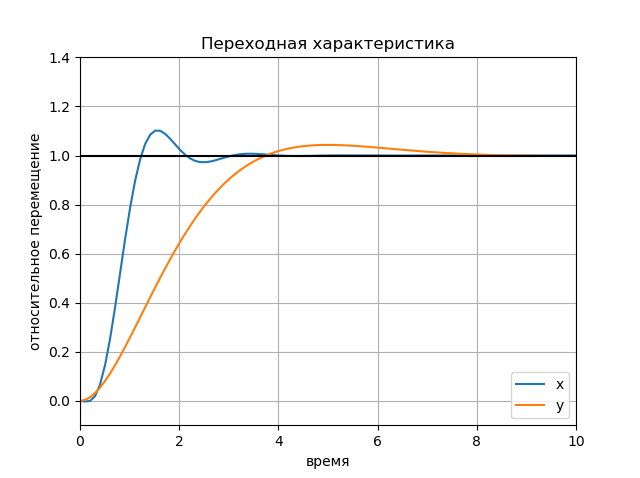 チャート:
チャート: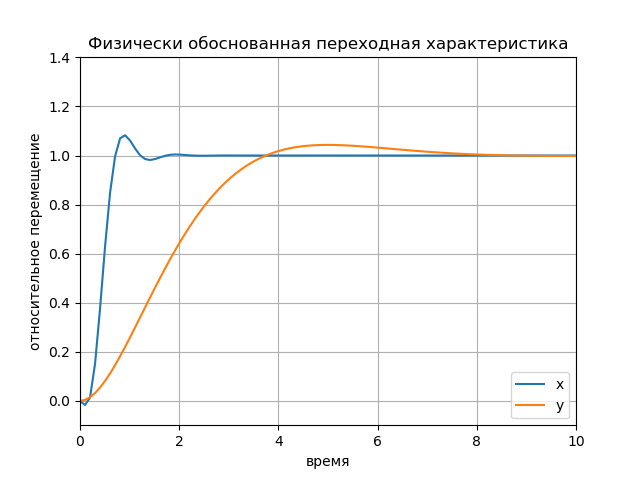
結論:
新しいlqr()関数の使用を考慮に入れた、出版物に示された航空機でのLQR最適化の実装により、制御理論の対応するセクションを研究する際にライセンスプログラムMATLABの使用を放棄することができます。
参照資料
1.
指の数学:線形2次コントローラー。2.
最適な制御システムの設計の問題における状態空間。3.
Python制御システムライブラリを使用して、自動制御システムを設計します。4.
Python制御システムライブラリ。5.
Python-slycotモジュールをスパイダーにインポートできません(RuntimeErrorおよびImportError)。6.
Pythonコントロールシステムライブラリ。7.
電気駆動での最適制御とlqr最適化の基準。