磁石は古代から人々に親しまれてきましたが、強磁性の物理学は謎のままです。 今、おなじみのパズルは、物理学者を質問に答えることにより近づけます
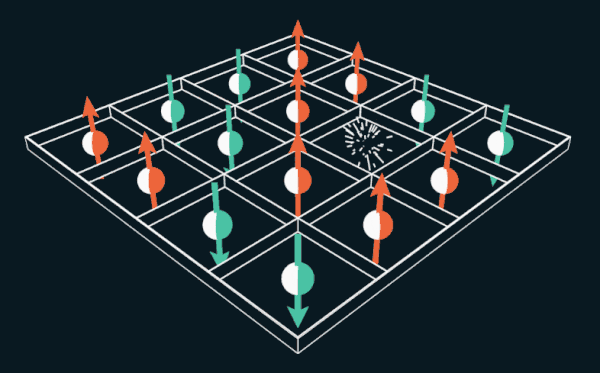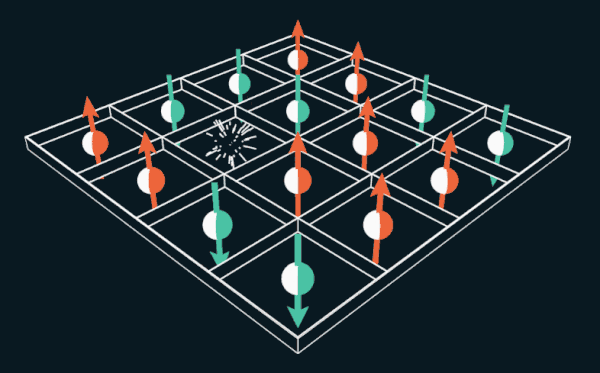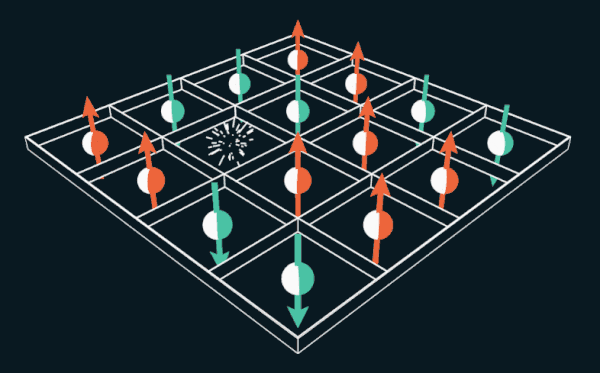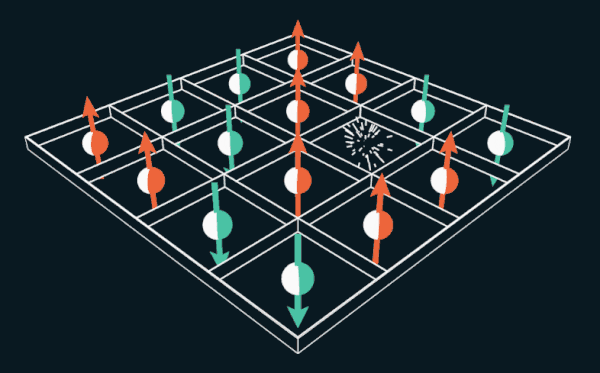 15のゲームでは、プレイヤーはグリッド内で番号付きのタイルを移動できます。 数値が電子スピンに置き換えられた場合、パズルを使用して永久磁石がどのように機能するかを説明できます。
15のゲームでは、プレイヤーはグリッド内で番号付きのタイルを移動できます。 数値が電子スピンに置き換えられた場合、パズルを使用して永久磁石がどのように機能するかを説明できます。1880年の数ヶ月間、米国の全地域が中毒に陥りました。 1880年3月12日にカンザス州インペリアで開催されたThe Weekly News-Democrat誌は、「流行が全国的に文字通り噴火しました」と述べています。 流行はヨーロッパに広がり、ニュージーランドとともにオーストラリアにまで達しました。
この病気は新しい情熱になりました。単純な機械パズルのおもちゃ「15」を思いとどまらせることです。 まだ知られており、4 x 4の正方形のフィールドで構成されており、15個の番号付きタイルを移動して順番に並べることができます。
今日の標準では、このゲームは時代遅れに見えますが、1880年には人気のピークに達しました。 「このような娯楽に抵抗することのできる子供はいません。大人が彼女の魅力を逃れるほど強くも慢もいません」と新聞は書いています。 そして、この失望は、このパズルの構成の半分しかうまく解決できないという数学的に証明された事実に起因する可能性があります(おそらく影響を受けた人には知られていない)。
ほぼ140年後の今日、「15」ゲームへの関心が再び復活しましたが、今回は気を散らすものとしてではなく、一見無関係ではるかに複雑なパズルを理解する方法として機能します。
冷蔵庫のドアに掛かっているような永久磁石は、
強磁性などの現象に惹かれます。 強磁性体では、電子のスピンが整列し、一緒になって磁場を生成します。 より正確には、鉄、コバルト、ニッケルなどの金属は、その電子が材料内を自由に移動できるため、バンド磁性を示します。 各電子には独自の磁気モーメントがありますが、これらのすべてのモーメントが磁石内でどのように、またなぜ並んでいるかを理解するには、すべての電子間の量子相互作用を計算する必要があります。
「ゾーン磁気は、実際には、理論的な凝縮物質物理学における最大の課題の1つです」と、ジョンズホプキンス大学の物理学者Wai Lee氏は述べています。
しかし、リーと2人の大学院生であるエリックボブロフとキートンスチュービスは、この問題の解決に少し近づいたかもしれません。 数学パズル「15」を使用して、彼らはゾーン磁気の理想的な状態を記述する有名な定理を拡張しました。 ジャーナルPhysical Review Bに掲載された新しい
分析では、定理を拡張してより広くより現実的なシステムを説明し、磁石のより正確なモデルにつながる可能性があります。
「すばらしい仕事です」と、カリフォルニア大学サンディエゴ校の物理学者
ダニエル・アロバスは言いました。 「ゾーンの磁気に関する詳細な結果が少なすぎて断片化されているため、この作品が特に気に入っています。」
ホールジャンプ
最も基本的なレベルでは、金属内の電子は2つの主要な制限に従う必要があります。 まず、それらはすべて負に帯電しているため、互いに反発します。 第二に、いわゆる電子に従うために電子が必要です パウリの原理は、2つの粒子を仮定しています[半分の整数スピン/約。 トランス。]同じ量子状態にすることはできません。 これは、同じスピンを持つ電子-電子の磁気モーメントに比例する-は、金属原子で同じ状態を占有できないことを意味します。 そして、反対のスピンを持つ2つの電子ができます。
電子グループのパウリ原理の相互反発と制限を満たす最も簡単な方法は、それらを分離し、スピンを揃えることです。その結果、材料は強磁性になります。
ただし、これは単純化した図にすぎません。 物理学者は、個々の電子間の無数の量子相互作用から、整列したスピンのこのような組織化されたパターンの出現に関する詳細なモデルを構築できませんでした。 たとえば、リーが説明したように、電子の波動関数-その量子特性の複雑な数学的記述-は、別の電子の波動関数と混同される可能性があります。 個々の粒子の振る舞いが強磁性のような集合現象の出現にどのようにつながるかを完全に理解するには、システム内の各電子の波動関数をモニターする必要がありますが、相互作用の過程で残りの各電子の波動関数を連続的に変化させます。 実際には、このような広範囲にわたる絡み合いにより、強磁性を記述するために必要な完全で包括的な方程式を書き留めることができなくなります。
代わりに、リーを含む物理学者は、強磁性の背後にある物理学を記述する単純化され、理想化されたモデルを研究することによって情報を収集しようとしています。 特に、彼女の最新の作品は、50年以上前になされた重要な発見を拡張しています。
1960年代半ば、地球の反対側から来た2人の物理学者が独立して証拠を導き出し、電子が整列して強磁性状態を形成する理由を証明しました。 当時ケンブリッジ大学で働いていた物理学者であるデイビッド・テュールズは、2016年にノーベル賞を受賞し、名古屋大学の物理学者で当時サンディエゴのカリフォルニア大学を訪問した長岡洋介は、それぞれ1965年と1966年に証拠を発表しました。 。 彼らの結果は、長興チュールの定理(または単に長置定理)と呼ばれ、原子格子上にある理想的な電子系に基づいています。 そのため、実際の磁石の振る舞いについては説明していませんが、それでも重要であり、原則として初めて電子スピンを整列させる必要があることを示しています。 そして、それらの分析は数学的証明であったため、物理学に典型的な近似を負担することなく、正確でした。
定理を理解するために、2次元の正方格子を想像してください。 各ノードは反対のスピンを持つ2つの電子を収容できますが、定理は2つの電子を1箇所に配置するには無限のエネルギーが必要であることを示唆しています。 これにより、各場所に1つの電子のみが存在することが保証されます。 この構成では、各電子はスピンを上または下に向けることができます。 それらは整列する必要がないので、そのようなシステムは強磁性体であってはなりません。
 ジョン・ホプキンス大学の物理学者、ワイ・リー
ジョン・ホプキンス大学の物理学者、ワイ・リー次に、1つの電子を削除します。 その結果、穴と呼ばれる空いている場所ができます。 隣接する電子が穴に滑り込むと、新しい空の空間が残ります。 別の電子が新しい空の場所に移動し、別のホールを残します。 この例では、実際、穴はある場所から別の場所にジャンプし、グリッドの周りを移動します。 Thulesと長岡は、この場合、単一のホールが追加されると、電子が自発的に整列することを発見しました。 彼らは、それが最もエネルギーの少ない状態、つまり強磁性体の状態であることを証明した。
Arovasは、システムが最も低いエネルギーの状態になるためには、電子スピンの構成を乱すことなくホールが自由に移動できる必要があると説明しています。そのようなプロセスには追加のエネルギーが必要です。 しかし、穴が移動すると、電子も移動する必要があります。 スピンの構成を乱すことなく電子が移動するには、電子を整列させる必要があります。
「長岡定理は、強磁性の個々の事例を数学的に証明できる数少ない例の1つです」と東京大学の物理学者である
押川正樹は述べた。 「しかし、物理学の観点から見ると、これは非常に人工的なものです。」
たとえば、電子は相互反発を克服して一箇所に収まるために多くのエネルギーを必要としますが、定理が要求するように無限ではありません。 さらに、長岡とテュールによって描かれた絵は、単純な格子にのみ適用されます。正方形または三角形で構成される2次元格子、または3次元立方格子です。 自然界では、強磁性はあらゆる種類の構造を持つ多くの金属で発生します。
長興テューレスの定理が実際に強磁性を説明している場合、それはすべての格子に適用できるはずです。 人々はそれがそうであると仮定した、リーは言った。 「しかし、誰も本当の、明確な証拠を与えませんでした。」 まあ、それはまだです。
背中のあるタイル
1989年、学習院大学の物理学者であるハル・タサキは、この定理を拡張して、格子が接続性などの数学的特性を持っている限り適用可能であることを発見しました。 移動する穴が1つある単純な正方格子の場合を考えます。 ホールを移動することにより、電子の数を維持しながら、スピンの構成を再現でき、スピンを上下に向けることで、接続条件が満たされます。
しかし、正方格子と三角格子、および3次元立方体は別として、他の場合に接続条件が満たされるかどうか、したがって、この定理をどの程度広く適用できるかは不明でした。
この問題に対処するために、リーは六角形のハニカムグリッドから始めました。 このタスクに取り組んでいる彼女の生徒、BobrovとStubisは、それがXIX世紀のマニア、つまりパズル「15」に似ていることに気付きました。 タイルラベルを数字から裏へ、上下に入れ替えると、パズルは長木強磁性体と同等になり、穴が電子格子に沿って移動します。
パズルは、タイルを任意の順序で再配布する機会があるときに許可されます。これは、接続の状態と完全に一致します。 したがって、与えられた格子に対して連結性条件が満たされるかどうかの問題は、そのような構造の格子上で同等のパズルを解くことができるかどうかの問題になります。
1974年、現在カリフォルニア工科大学で働いている数学者リチャードウィルソンが、すべてのグリッドのパズル「15」を要約して解くことにより、
この問題を解決したことがわかりました。 証拠の一部として、彼は、ほとんどすべての分離不可能なラティス(いずれかのノードを削除した後でもすべてのノードが接続されたままである)で、移動数が偶数である限り、タイルを移動して任意の構成を取得できることを示しました。 唯一の例外は、単一のポリゴンが三角形よりも大きく、「グラフθnull」と呼ばれるもので、六角形の中心の頂点が2つの反対の頂点に接続されていることです。
研究者は、ウィルソンの証明を長岡チュールの定理に直接適用することができました。 彼らは、2次元ハニカムや3次元ダイヤモンド型格子などの一般的な構造を含む、ほぼすべての格子上の電子系と単一のホールに対して接続条件が満たされることを証明しました。 2つの例外-三角形より大きなポリゴン、およびグラフθnull-いずれの場合でも、実際の強磁性体では発生しません。
穴爆発
「15」パズルを使用することは、新鮮で潜在的に実り多いアプローチです、とカリフォルニア大学サンタクルーズ校の物理学者、
スリラム・シャストリは言いました。 「私は、彼が新しい言語、グラフ理論との新しいつながりをもたらしたという事実が好きです」と彼は言いました。 「これは豊かなつながりだと思います-将来、それは豊かなアイデアの源になるかもしれません。」 しかし、研究は大きく前進していますが、問題は残っています。
厄介な問題の1つは、格子に沿って移動する際に移動する穴が奇数のステップを踏む必要がある場合、長木-チュールの定理が常に機能するとは限らないことです。 おそらく最も顕著な問題は、定理が正確に1つの穴の存在を必要とすることです-それ以上でもそれ以下でもありません。 ただし、金属には穴がたくさんあり、多くの場合、格子の半分まで占有します。
しかし、物理学者は多くの穴のあるシステムの定理を一般化しようとしました。 物理学者
は 、数値法を使用し
て 、長木の強磁性が有限サイズの正方格子で機能するように見えること
を示しました。 現在の研究では、研究者は正確な分析技術を2次元ハニカムと3次元ダイヤモンド型格子に適用しました。 穴の数が格子ノードの数を超えない限り、セルの場合は1/2度、ダイヤモンド型の格子の場合は2/5の長沖強磁性が存在するようです。
これらの正確なソリューションは、ゾーン磁気のより完全なモデルにつながる可能性があります。 「これは、将来の研究のための厳密な数学的出発点を設定するための小さな一歩に過ぎません」とリー氏は言いました。